刮板输送机链轮的逆向设计及建模

范鹏程，魏抗抗，王 龙，卢其文，程龙超

(上海中联重科桩工机械有限公司，上海 201612)

0 引言

第一运输机(简称一运)是悬臂式掘进机的重要系统组件之一，其功能是不断地把物料从铲板部运输到第二运输机，因此其设计质量的好坏直接决定了掘进机的工作效率。而链轮链条则是一运的核心零件，一运的运输功能是通过链轮链条的不断啮合得以实现，因此链轮链条的设计水平间接决定了掘进机的工作效率[1]。

链轮以往是在确定链轮的齿数、链条的节距及直径后，通过理论经验公式计算出链轮的节圆直径、外径及链窝等相关参数进行设计的。这种靠理论经验公式设计出来的链轮与实际模型之间难免会存在较大误差，因为链轮链条啮合时精度要求很高，稍有偏差都可能导致设计的链轮出现严重的质量问题[2]。

本文采取逆向设计的思路，将理论经验公式与实际建模相结合对链轮进行设计。首先对链条进行选型，然后在现有的理论基础上计算出链环的理论半径，总结出链环半径的计算公式，绘制出链环模型，最后在链环模型基础上对链轮进行设计。

1 链环的设计及建模

1.1 链环理论分析

链环是由相等数量的立链条与平链条交替组成的封闭圆环，理论上平链条刚好和链轮的齿形进行啮合[3]。组成链环的链条总数n与链轮的齿数z存在以下关系：

n=2z.

(1)

图1为链轮齿数为5时的链条成环示意图。由图1可知，当选定链条并确定链轮齿数后，链环的实际分度圆半径R也随之确定。下面分析讨论如何通过链条直径d、链条节距p以及链轮齿数z计算出链环分度圆半径R。

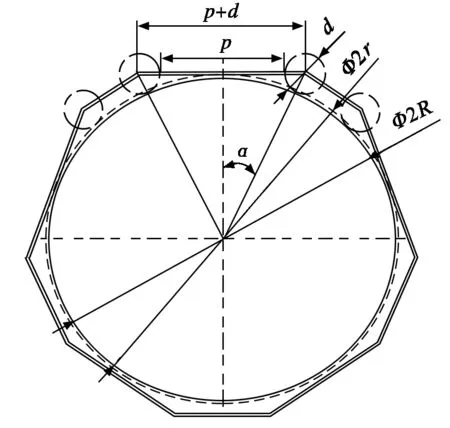
图1 链轮齿数为5的链条成环示意图

如图1所示，一个平链条在链环中所对应的分度圆夹角为2α，2α与链条直径d、链条节距p以及链轮齿数z理论上存在如下关系：

α=[(d+p)/(4pz)]×360°.

(2)

则理论上链环的分度圆半径r为：

r=(d+p)/(2tanα).

(3)

实际上，由于多边形逼近圆环时存在误差，理论上计算得出的分度圆半径r也相应存在误差。经与实际模型对比计算可知：当齿数为5时分度圆半径误差仅为0.75%，且误差随着齿数的增大而减小；当齿数为36时分度圆半径误差则为0.016%，完全可以忽略；当齿数大于36时，则可认为实际分度圆半径R与理论分度圆半径r相等。则链轮齿数z与误差系数γ近似有如下线性关系：

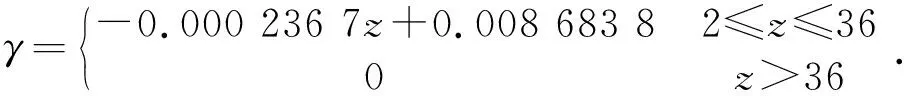
(4)

因此，实际的分度圆半径R为：

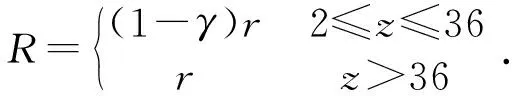
(5)

1.2 链环设计及建模

由链条成环计算公式及输入的相应变量可得到链条成环计算表，如表1所示。表1中有3个变量参数，分别为链条直径d、链条节距p以及链轮齿数z，当确定了这3个参数的具体数值后则可通过链条成环计算公式得到链环的分度圆夹角以及分度圆半径，使得能更快速方便地设计出链环。

表1 链条成环计算表

由表1可知，链条直径为30 mm、链条节距为108 mm及链轮齿数为5时所对应的分度圆半径约为161.33 mm。利用Creo6.0软件对其进行建模可得到所设计的链环模型，如图2所示。

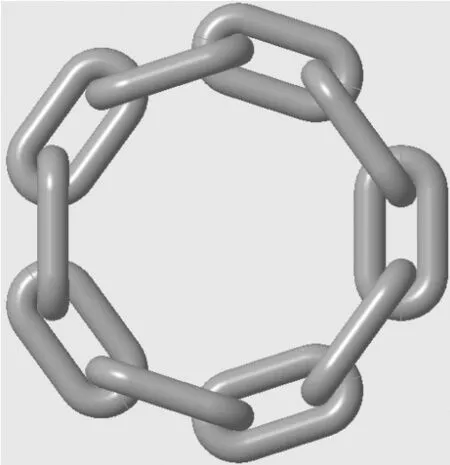
图2 链环Creo6.0模型

2 链轮的逆向设计及建模

2.1 链轮理论分析设计

设计出链环后，在链环的基础上逆向设计链轮。链轮的设计重、难点在于齿形及链窝的设计，需要计算链窝、齿形等相关参数。而基于链环逆向设计链轮，则可以完全借助链条的运行轨迹完成对链轮齿形及链窝的设计，不用再计算齿形、链窝等相关参数，达到事半功倍的效果。

根据驱动装置链轮轴的尺寸，可确定2个参数，即链轮内孔直径以及链轮的长度[4]，链轮的其他外形尺寸则可通过计算得到。选定链轮齿数z，则链轮节距角θ为：

θ=π/z.

(6)

选定链条的直径d以及链条节距p，则链轮节圆直径为：

(7)

一般情况下，考虑到链条链轮实际运行过程中存在磨损，则需要将计算得到的链轮节圆直径D0进行圆整[5]。

链轮外径Dg为：

Dg=D0+2d.

(8)

通常情况下，为增加链齿的承载能力，可将链轮外径适当减小。

链轮立环立槽直径Df为：

(9)

其中：b与Δ为链条型号对应的系数，可参考机械手册查询。

短齿齿厚W为：

W=(2H+d)sinθ-Acosθ+d.

(10)

(11)

A=1.075p+d.

(12)

其中：H为链轮中心至链窝底平面距离；A为链窝中心距离。

2.2 链轮Creo6.0建模

链轮的设计建模重点是齿形以及链窝的建模。在设计好图2的链环后，链轮的设计建模过程如下：

(1) 根据上文的理论分析公式计算得到链轮的节圆直径、外径等参数，确定链轮的整体轮廓。

(2) 根据链环确定链轮外齿形的轮廓设计，如图3所示。

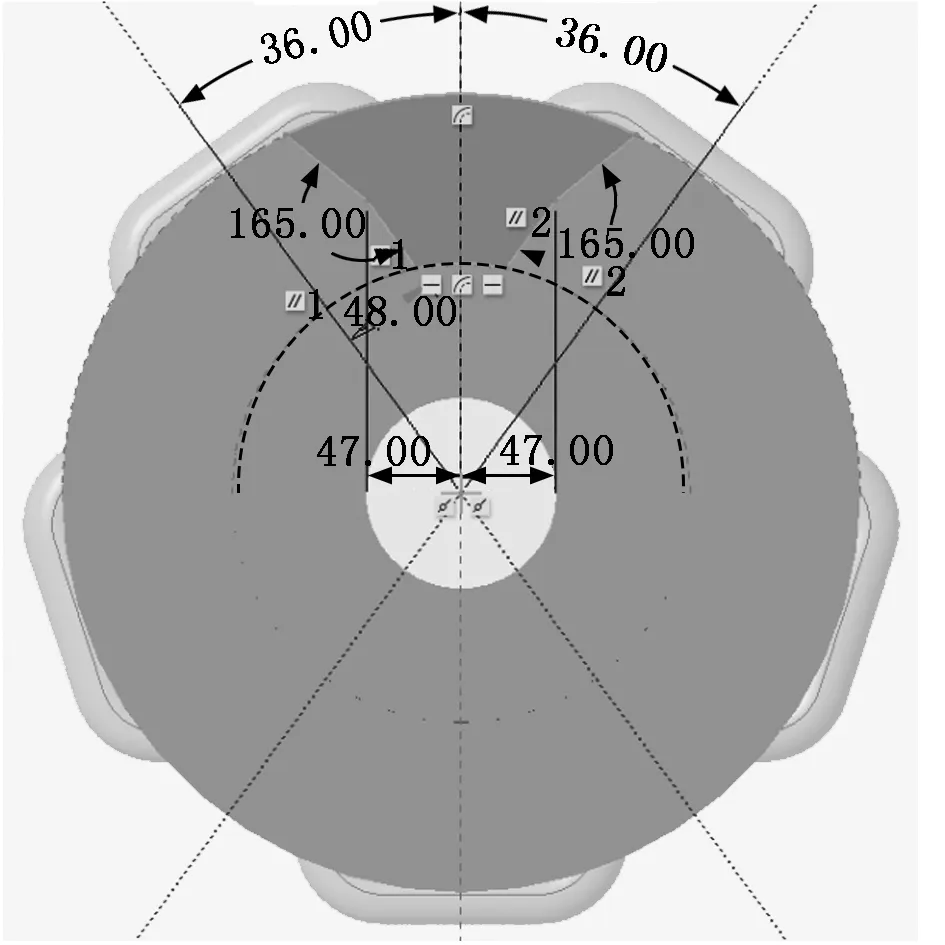
图3 链轮外齿形的轮廓设计

(3) 根据链环及外齿形确定链轮内齿形的轮廓设计，如图4所示。

(4) 对链轮的模型进行圆整，即完成对整个链轮模型的设计，如图5所示。

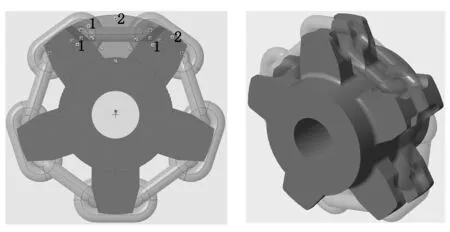
图4 链轮内齿形的轮廓设计 图5 链轮Creo6.0建模

3 结语

本文创造性地提出链条成环的计算公式，精准地对链环进行建模设计；在链环的基础上对链轮进行逆向设计，系统性地给出了链轮的设计流程，提高了链轮的设计精度。本文对链轮所做的研究设计，对其他链轮的设计及建模流程具有一定的借鉴作用。