促进学生深度学习的教学策略
赖加种
(福建省泉州市洛江区罗溪中心小学,福建 泉州)
一、巧设问题,促进深度学习逐层推进
有效的问题创设能引起学生认知心理的“失衡”,教师根据教材内容,创设新颖别致、富有悬念的问题情境,使学生处于“不愤不启、不悱不发”的不平衡状态,激发学生强烈的思考欲望,使学生更加专注地探究问题。亚里士多德曾经说过:“思维自疑问和惊奇开始。”让学生可以主动参与到课堂活动当中,并且积极回答教师提出的所有问题,让学生在问题当中展现自我,激发自身的潜能,培养自身的主观能动性和创造能力。一个问题从提出到解决,需要一个逐渐深入探索的过程,学生在问题解决的过程中促成高阶思维的发展和综合素养的提升。所以教师应该根据学生的个体差异性和发展情况制订阶梯式的问题,对于基础较差的学生应该提问简单基础的问题,使问题的内容更具呈现力、类型更多样,为学生打造一个较为轻松愉快的学习环境,使学生全身心地投入到当中,激发学生最大的潜能,充分发挥深度学习的作用和价值。
例如,在教学“用字母表示数”一课时,让学生围绕以下问题思考与探究。
(1)你们知道扑克牌中的字母A、J、Q、K分别代表什么数吗?
(2)你们今年几岁?(大部分学生是11岁)猜一猜老师今年的年龄。(45岁)老师比你们大多少岁?相差多少岁?(34岁)
(3)当你20、30、31、35、40、50……岁时,老师几岁?一直写下去能写完吗?
(4)如果你ɑ岁,你能用字母表示老师的岁数吗?(ɑ+34)你认为这里的字母ɑ可能是多少岁?可以是200吗?为什么?
以上四个问题把老师的岁数、学生的岁数、相差岁数字母ɑ三者之间的信息置于其中,学生体会到字母不仅可以表示具体数量,式子a+34还可以表示数量之间的关系,用字母表示数的取值范围是由实际情况来决定的。教师应该从传统的思想观念转变到适应现如今发展的新教育改革的理念,充分发挥学生的独立自主能力和创造力,使学生可以根据此问题举一反三,充分理解和掌握所有的理论知识,在数学教学时,应该让学生对数学公式和数字的含义进行了解,从而促进学生解决数学问题的能力和意识的形成,激发学生的思维活跃度和灵敏度。
二、亲身体验,促进深度学习真实发生
数学课程的展开主要是为了激发学生的思维灵敏度和活跃度,使学生充分发挥主观能动性和潜能,不断地去交流、比较、推理,实现知识本质的深度建构。因此,教学中教师要根据学生已有的经验和思维水平设计学习活动,让学生亲身经历将实际问题抽象成数学模型的过程,提高学生的积极性,使学生对理论知识和实践活动有更深层的认识和见解。当教师举办一系列教学活动时应该让学生主动参与进来,因为只有学生主动参与,才能促进学生成长。
如教学“植树问题”时,出示课本情境图:五年级学生在一条长100米的小路植树,每隔5米栽一棵,一共要栽多少棵树?师:同学们先估一估,然后小组尝试解决?学生四人一组,讨论解决植树问题,学生动手操作,画图模拟植树。这样的体验式的学习相对开放,拓展了学生的思维。在小组学习合作交流时,学生很快进入思考的状态。在沟通环节我们惊喜地发现,一些学生提出了很有价值的数学问题。如他们会发现:有的学生说100米距离太长,模拟植树很麻烦,浪费时间,有更快的方法吗?有的学生说可以缩短路的总长度进行试验,选择50米、30米、20米……就可以推出100米的小路一共要栽多少棵树。还有的学生提出是首尾都栽树吗?要是碰到一端有电线杆或房子怎么办?在小组的汇报中,学生情绪很高,接下来学生就“怎样植树”的疑问又展开了思考,得出了几种结论:两端都栽、只栽一端、两端都不栽。教学中,教师的放手、学生的亲身体验、思考水平的拓展才能使学生有机会进入深度学习。
深度学习是为了让学生体会更加具有挑战性和更高难度的内容和任务,当然离不开教师合适的引领。在课堂教学中,教师可以设计一些体验性的学习活动,如游戏、故事情境、实践操作等活动,让学生以小组为单位,每个人都有合理的分工,都有事情做,让学生可以感受到学习的乐趣,培养学生综合素养能力和意识,促进学生对数学理论知识的掌握,促使深度学习真实发生。
三、适时思辨,促进深度学习有效开展
思辨是深度学习的核心,只有让学生对思辨有更深层次的见解和掌握,才能最大限度地发挥学生的潜能。思辨的目的是让学生对教师所提出的问题不断分析并解决。余文森教授认为:“不会思考的学生,只能获得假知识。”学生的自我思考、自我反思等方面都能在一定程度上提高学生的思辨能力。
因此,教学中教师要引导学生经历充满思辨的学习历程,包容多种答案或解法的设问,思考问题背后的问题,从而引发学生多样化地思考。在重要环节当中应该提出开放性的问题,让学生展开讨论,引发学生对问题的思考。在教学中教师要设计值得争辩的问题驱动学生的思辨活动,值得争辩的问题往往是知识的核心,不仅如此还是教学活动当中的重点内容,让学生可以在不断思考、不断分析当中提高自身的思维能力,从而体现出深度学习的作用和价值。
例如,教学“平行四边形的面积”一课时,在面积计算的方法上,是“邻边相乘”还是“底高相乘”,学生最易出错,约30%的学生选择“邻边相乘”这一错例,是什么原因造成的呢?笔者认为是由“长方形面积=长×宽的计算方法引起的负迁移”;为避免学生出错,深入理解平行四边形面积与底、高、邻边的本质关系。教师可引导学生展开辩论,在思辨中促进知识的正迁移。
如图:一个平行四边形的底是7厘米,高是4厘米,邻边是5厘米,它的面积是多少平方厘米?(学生在做题时出现两种做法)

(1)引发冲突:
师:“为什么同一个平行四边形的面积,有的答案是28,有的答案是35呢?同一个图形的面积有可能出现两种答案吗?”
生齐:“不可能。”
师:“到底哪一个答案是对的呢?请同学们先在小组讨论,再派代表辩论好吗?”
(2)汇报辨析:
生1(选择“35”的,底边×邻边):“把平行四边形框架拉伸后变成长方形,长和宽都不变,面积7×5=35。边说边用尺子量一下斜边是5厘米,拉伸后还是5厘米,所以面积不变。”(有的学生点头表示同意)
(选择“28”的学生听后直摇头)
生2(选择“28”的,底边×高)拿着平行四边形的框架模型边演示边说:“这条斜边是5厘米,拉伸成长方形后长度不变还是5厘米,但是中间的距离变长了。”
师:“你观察得真仔细,邻边5厘米是没有变,但是中间的距离变长了,说明什么变了?(生:高变长)”(师利用平行四边形教具在黑板上演示,见图1)
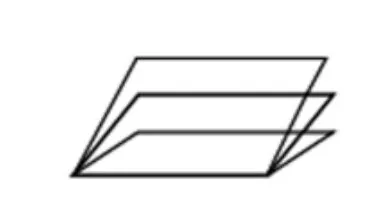
图2平行四边形拉动的示意图

图1
教师课件演示:(引导学生观察,不断演示拉动平行四边形过程,图形从最大拉伸到最小,见图2),引导学生观察,平行四边形的面积有发生变化吗,周长呢?
生1:“周长不变,四条边还是一样长。”
生2:“面积变小,因为平行四边形拉伸变小时,底不变,但高在缩短。”
师(教师继续边演示课件边说):“如果把缩小了的平行四边形框拉上去一点,面积会怎样?什么原因?”
生齐:“面积变大了,因为高在变化。”
师:“如果要把图形的面积拉伸成最大,怎样操作,面积最大是多少?”
生齐:“把平行四边形框拉成长方形,面积是最大的,面积是7×5=35。”
师:“现在知道平行四边形的面积是35还是28吗?”
生齐答:“是28。”
师:“说说平行四边形的面积的大小是由什么决定的?”
生齐答:“高。”
师:“只有高决定面积的大小吗?”
生1:“还有底边。当底相等,高越大,图形的面积越大”。
师:“如果知道底和高,怎样求平行四边形的面积?”
生齐答:“平行四边形的面积=底×高。”
在欢快的争辩中,学生明白了平行四边形框在拉伸过程中面积和底、高、邻边的变化,明白了为什么不能用“底边×邻边”求出平行四边形面积。
在教学过程中,适当引导学生进行思辨,使他们在与他人交换信息的过程中深化自己的认识,自觉及时进行修正,使自己的知识体系更趋于完善,并且在思辨中发展了学生的思维灵敏度,让学生感受到数学知识的魅力,与同学的不断交流、不断讨论更能提升学生的主动能动性,使学生对思辨有更深层次的认识和了解,从“深层思考”走向“深刻思辨”。
四、适当拓展,促进深度学习持续发展
数学课的拓展主要是针对学生在已经掌握的理论知识当中对其他知识进行延伸,或者是可以运用掌握的理论知识解决其他的问题。拓展在数学教学活动当中是非常重要的存在。数学课程当中的内容是一环套一环,所有的概念和公式都可以运用到数学问题当中,因此需要让学生对整体单元或者是整个课本有更深层次的认识和掌握,不能过于追究某一知识,教师应该根据学生的个体差异性设计合理的问题,如基础题、复杂题、拓展题等,让学生可以充分体会到数学理论知识的魅力。因此,数学“拓展延伸”已成为教学的有机组成部分,要努力做到目标“适度、有效”,就必须“精挑细选”拓展内容和延伸形式,适当控制拓展容量,精准把握延伸时机,联系新知、拓展新知、解决未知,实现数学知识的同化与顺应,达到拓宽学生的思维空间。
例如,学了“植树问题”后,当学生建构“两端都栽时,棵数=间隔数+1”的数学模型后,学生对植树问题进行掌握和解决后,教师可以拓展其他的问题,如安装路灯等,让学生展开思考和讨论:安装路灯等问题跟植树问题有什么关系?不仅可以让学生加深对植树问题的掌握,还能举一反三,解决其他现实问题。然后再引导学生进行逆向思维,对问题进行相应的思考,从而可以分析出“两端都不栽,棵数=间隔数-1;只栽一端,棵数=间隔数”的数学模型,学生在拓展中明白了植树形式的不同,棵数和间隔数也不同,让学生可以对植树问题模型的建构有更深层次的理解,并且可以根据此模型举一反三,实现“植树问题”不一定是植树的模型思想的渗透,而是要体会数学思想方法的应用性。教师适当地拓展,从而让学生不断体会、感悟、深化数学思想方法。在一定程度上提高了学生分析问题的能力,有效促进了学生学习的拓展迁移能力。
再比如,学习了“比和比例”之后,我让学生测量并计算操场上旗杆的高度。面对又高又滑的不锈钢旗杆,大多数学生摇摇头。这时,有学生建议攀爬上去测量,马上有学生反对说旗杆太高,攀爬危险。也有学生建议先测量绳子的长度再升起国旗,并将绳子除以2,就是旗杆的高度,关键是怎样把绳子绑在旗杆上呢?这时,老师抓住教学契机,拿起一根1米长的竹竿,把它立在旗杆旁边。这时恰好阳光高照,竹竿的影子立刻映照在地面,老师让学生测量出竹竿影子的长度是0.45米,学生好像有所发现,师:想一想,通过竹竿高度与影子长度的比例能测量旗杆的高度吗?学生们兴趣勃勃,讨论交流、动手测量、列式计算,最后得出结论:“旗杆的高度∶旗杆的影子长度=竹竿的长度∶竹竿的影子长度。”受到启发后,学生运用比例的知识很快计算出旗杆的高度。师强调:应该在同一时间内测量影长,你们知道为什么吗?(生:因为太阳在移动,影子也会变化的)师:现在你能用这个方法计算学校里大楼和手机信号塔的高度吗?回到教室后,我还让学生观看微视频“塔利斯巧测金字塔”的数学故事,学生们兴趣盎然,情绪极高。这不仅培养了学生运用所学知识解决实际问题的能力,还提高了学生自身对问题的理解能力、思维灵敏度等。
总之,有效的深度学习可以最大限度地激发学生的主观能动性和创造能力,让学生可以对数学知识有更深层次的见解和掌握,教学中只有不同的教学方式有机地结合起来,才能让学生从“显性”的数学问题中去发现“隐性”的知识和规律,真正领悟数学本质,进而培养良好的思维品质,提升学生的数学核心素养。

