基于梯度法的指纹方向场的FPGA 实现
张宜尧,徐银森,李健儿,陈勇,赵建明
(1.电子科技大学,四川成都 610054;2.四川遂宁市利普芯微电子有限公司,四川遂宁 629000;3.四川上特科技有限公司,四川遂宁 629201)
指纹自动识别系统(Automated Fingerprint Identification System,AFIS)具有重要的研究价值,其中,求取指纹方向场(Fingerprint Orientation Field,FOF)信息被认为是解决指纹自动识别处理中众多关键技术的一个重要辅助方式[1-2]。通常,采集到的原始指纹图像中,由于脊线和谷线具有局部恒定的方向,因此,这些指纹方向通常用于描述脊线模式,为进一步的指纹处理和识别提供有用的依据。在方向图的计算中,若从图像局部特性的角度考虑,通过对指纹图像划分出的局部区域进行计算处理便可以得到指纹纹路的方向场数据,即能得到指纹图像的纹路走向。通常,指纹方向场估计方法可以分为三类:基于梯度的方法、基于数学模型的方法和基于深度学习的方法[2]。
指纹方向场经常作为指纹算法中的一项重要参数,应用在许多处理环节,如指纹分割算法[3]、指纹图像增强[4-5]、指纹特征提取[6]等,故其计算方法对于整体指纹识别系统的性能有着显著的影响。
1 梯度法求取方向场
指纹纹线方向定义如图1 所示,文中FPGA 实现的方案是通过梯度的方法[7-8]来求取方向图。

图1 纹线方向定义
由于梯度描述了曲线变化程度最快的方向,因此像素点的梯度方向就和该像素点所在的指纹纹线相互垂直。其计算方法如下,首先将指纹图像(I)以W×W窗口划分为块,利用块内各个像素点的水平、垂直方向的一阶梯度Gx、Gy,根据式(1)以及式(2)计算出该像素块的水平、垂直统计方差Vx、Vy。之后,根据式(3)将两方向块统计梯度比做反正切,计算出该窗口内纹线的角度。
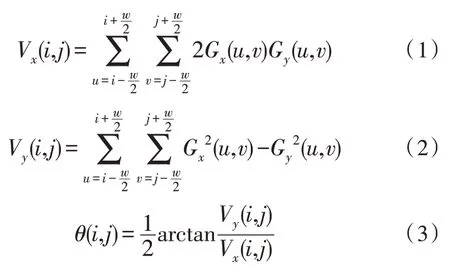
2 整体结构设计与实现
基于上述梯度算子求取方向图的算法,文中以FPGA 实现了该方向场计算模块,该模块主要由Sobel 算子模块(Sobel_cal)以及区域方向计算模块(Direc_cal)组成,其整体结构如图2 所示。输入包括时钟信号(clk)、异步复位信号(rst_n)、数据有效信号(IDVAL)以及指纹图像像素数据信号(Pixel);输出包括输出数据有效信号(ODVAL)以及角度数据信号(Direc)。下面分别介绍所采用模块的内部结构。

图2 整体结构示意图
2.1 Sobel算子模块
根据算法原理需要得到指纹图像像素点的一阶梯度Gx、Gy,避免对像素之间的插值点直接进行梯度计算的一种方法是使用3×3 邻域进行一阶梯度计算。常见的方式有Prewitt 算子、Sobel 算子、Robinson罗盘掩膜、Krisch 罗盘掩模、Laplacian 算子等[9]。文中采用的方法是利用索贝尔算子(Sobel operator)计算一阶梯度,有各种各样的Sobel 算子对,例如3×3、5×5 卷积核,3×3 Sobel算子如图3 所示。
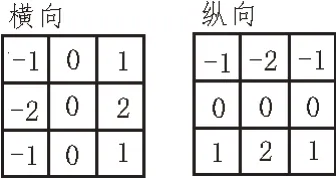
图3 Sobel算子
设3×3 区域中心指纹像素点为I(i,j),故可以得到其一阶梯度Gx、Gy的计算公式如下:

该部分模块结构图如图4 所示。考虑到Sobel算子计算一阶梯度时需要3×3 像素,所以利用基于RAM 的位移寄存器(shift register RAM-based)作为像素行缓存(Line-buffer),用于缓存指纹图像的三行像素数据。由于指纹像素输入以从上到下、从左到右的顺序逐拍将像素输入进行缓存,因此,只要设置行缓存数据宽度为指纹图像的行宽度,就能够对齐指纹图像的三行像素,并在行缓存末端随时钟逐拍输出对齐的三个像素[10]。

图4 Sobel算子方差计算模块结构图
之后,以逐像素位移(shift-in)的方式通过乘加器(Multiply Accumulate,MAC)与两个Sobel算子(图3)中系数先相乘、后相加,得到每一行乘加结果(Mac_x0…x2、Mac_y0…y2)。最终,通过平行加法器(Parallel-Adder,PA)将3 行乘加结果相加得到卷积结果,即每一像素的一阶梯度。
2.2 区域方向计算模块
区域方向计算模块(Direc_cal)的结构示意图如图5 所示,主要包括单点像素梯度方差计算逻辑(Pixel_Vx&Vy)、计数器0-2(cnt0、cnt1、cnt2),块方差寄存器(Vx_reg0…N-1,Vy_reg0…N-1)以及反正切计算模块(ATAN)。根据式(1)以及式(2),不妨令单点像素梯度方差为P_Vx、P_Vx,则得到:
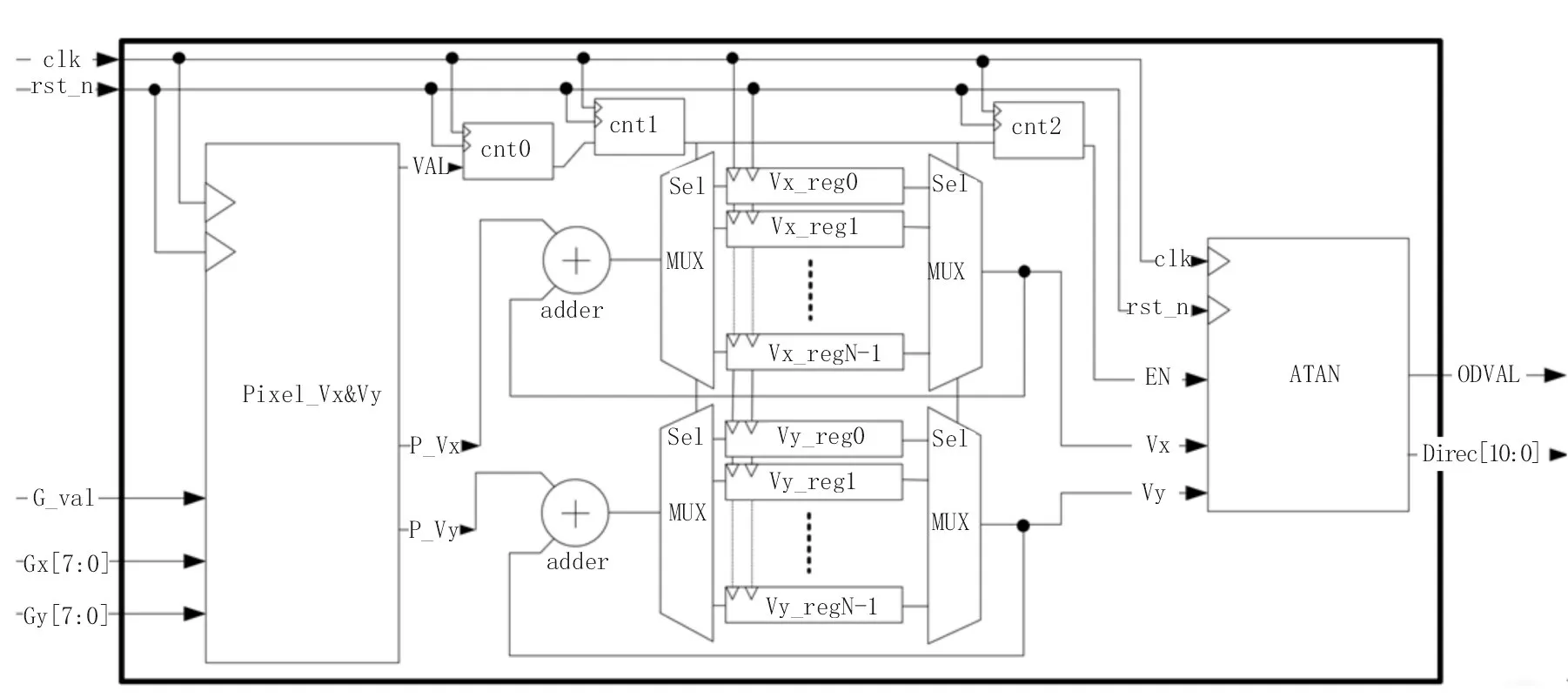
图5 区域方向计算模块结构图

由Sobel 算子模块得出的Gx、Gy作为单点像素梯度方差计算逻辑(Pixel_Vx&Vy)的输入信号,能够得到P_Vx、P_Vy,从而完成式(6)以及式(7)的计算。
之后是对方差结果统计式(8)及(9)的实现,不妨设指纹图像以W×W窗口划分为M×N块,确定出Vx、Vy寄存块的数目为N-1 个,再逐拍将P_Vx、P_Vy通过加法器(Adder)累加至块方差寄存器(Vx_reg0…N-1,Vy_reg0…N-1)中。同时,计数器0(cnt0)对P_Vx,P_Vy的输出进行计数,每当计数至W-1 时,计数器0(cnt0)清零且计数器1(cnt1)加一,从而控制多路复用器(MUX)切换方差累加寄存器;每当计数器1(cnt1)计数至N-1 时,计数器1(cnt1)清零且计数器2(cnt2)加一;当计数器2(cnt2)计数至W-1,且计数器0(cnt0)计数至W-1 时,则完成了一块区域的方差累加。每当完成一个块内的方差统计累加,则使能以反正切计算模块(ATAN)计算,得到块角度(Direc)。其中,反正切计算模块(ATAN)是基于坐标旋转数字计算(Cordinate Rotation DIgital Computer,CORDIC)算法实现的[11-12],其输出结果Direc 为11 bits 的有符号定点数,小数位为8 位。因此,在对应的输出弧度范围[-Π,Π]下,精度可以达到0.003 906 25。
3 仿真与测试
3.1 模块综合与仿真
所测试的对象为200×152像素的指纹,如图6(a)所示。在分块大小为8×8 像素的情况下,指纹图像被分为25×19 个区域,故该模块一共产生475 个数量的方向数据输出,输出的方向场数据如图6(b)所示。可以看出,该方式提取出的方向场与原指纹图像有着明显的对应关系。通过Quartus Prime 对文中所述FPGA 模块进行编译综合,并在Modelsim SE 下进行仿真,得到的模块仿真输出波形如图7 所示。

图6 测试指纹及其方向场

图7 模块仿真输出波形
3.2 方向场质量评估
为测试指纹图像采用不同区域分块大小对生成方向场的影响,对模块中分块大小进行定义,分别以4×4、8×8、12×12 区域进行块方向计算,得到图8 所示的三个方向场。

图8 不同分块大小方向场
为对得到的指纹方向场的质量进行评估,引用一种方向场评价方法[13],其原理是依据自然指纹的方向场具有较强的局部连续性,而计算失准的方向场信息带来的不规则噪声会使局部连续性大幅降低。通过使用平滑滤波器对方向场进行平滑处理,得到局部连续性较好的方向场。因此,通过平滑前后方向场中方向改变的比例越多,则平滑前方向场的质量越差。文中所采用的滤波平滑方式如下:

通过式(10)以及式(11)将各个角度在W×W大小窗口内映射成横、纵向投影φx、φy,通过式(12)及式(13)对角度投影进行滤波计算,最终将滤波后的投影根据式(14)通过反正切映射成方向角度。式(12)、(13)中所采用的滤波器为5×5 大小的高斯算子[14],如图9 所示。
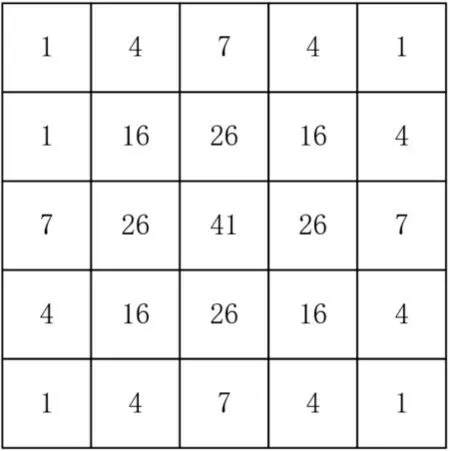
图9 5×5高斯算子
分别对图8 所示的三个方向场进行平滑处理,并统计其处理前后方向变化数目,得到平滑前后方向变化比例,如表1 所示。
由表1 可知,块大小对于方向场有如下影响:在4×4 小分块下进行分割得到的方向场虽然可以得到更多方向细节,且方向过渡更为平滑,特别是在指纹奇异点处,但是容易引入较多指纹原图像产生的方向噪声或毛刺,导致方向场质量不佳。而12×12 的较大区域分块会丢失较多方向信息,并且在分块边界处引入了更大的方向突变,从而使方向场的局部方向连续性大幅降低。
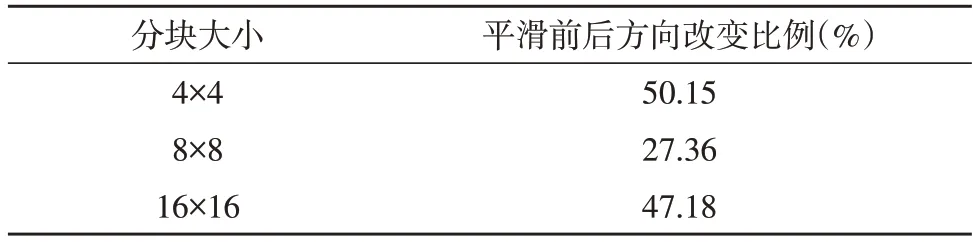
表1 平滑前后方向变化结果表
另一种常用的方法是通过八方向掩膜对指纹进行方向场提取[15]。从实验结果中列举出5 组相同大小不同身份的指纹样本,并将该模块采用梯度法得到的结果与掩膜法所提取方向场进行对比评估,如表2 所示。
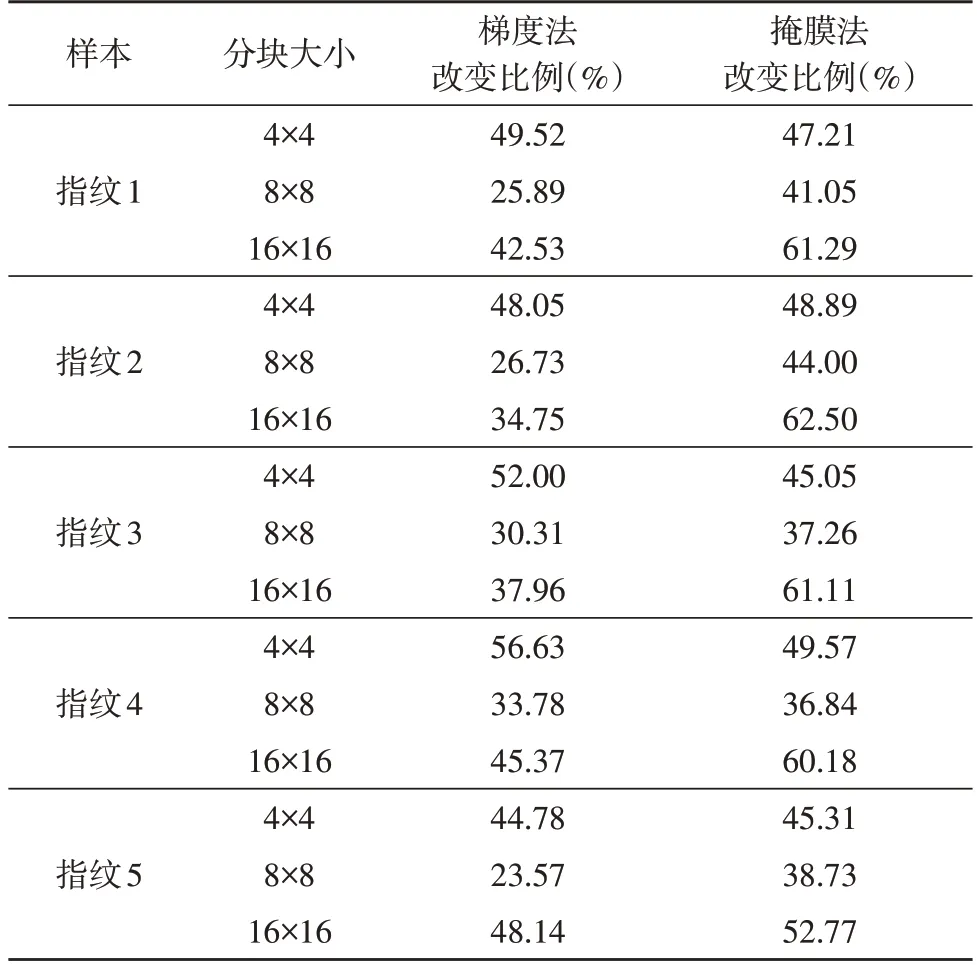
表2 梯度法与掩膜法对比结果表
4 结束语
文中提出了一种基于梯度法的指纹方向场的FPGA 实现方式,该方式能够较好地提取出指纹纹线方向特性,且由于方向场是以区域块的方式生成的,因此对于指纹图像中部分像素产生的噪声有较好的抑制作用,并且与传统基于方向模板方向场生成方式[16]相比,生成的方向数据拥有更高的精度,从而能够提取出更多奇异点方向特征信息,且生成的方向场更加平滑。该方案为后续指纹图像处理提供了强坚固性的纹线方向特征信息,从而间接提高指纹识别系统的性能。

