开管管口校正数与计温律高计算公式验证—基于黄钟律管的三组实验
□史凯敏、刘 勇
获取律管音高的基本方法有二:一为利用声学理论公式计算,二为制管验声。前者由于方便、简洁而受到多数研究者的青睐。然而,由于所采用的公式和管口校正数的差异,往往结论也很不一致。制管验声之法得到的结果应较为可信,但不可否认的是:因吹奏角度、力度等主观因素的差异的确会造成音高测定的不稳定。这种差异尤其在温度较低或口唇位置不一致的情况下尤为突出,因而,研究管律需要取得较为可信的管口校正数和计算公式。要实现这一目的,唯有制管验声,双向推导,算验相合,方得真数。
一、学界常用的律管管口校正数
目前,经研究者推定、使用的管口校正量(简称管校数)约有十种说法。(1)P.M莫尔斯的《振动与声》①〔美〕P.M莫尔斯:《振动与声》,南京大学《振动与声》翻译组译,科学出版社,1974年,第243页。认为,开口管管口校正量为8a/3π(a为半径)。(2)比利时声学家马容(V.Mahillon, 1841~1924)提出,开管管口校正量约等于管的直径2r,闭管管口校正量约等于半径r。②缪天瑞:《律学》,人民音乐出版社,1996年,第11页。(3)音乐声学家罗兴认为,开管管口校正数=2×0.61r,闭管管口校正数为0.61r(r为管的半径)③Thomas D. Rossing. The Science of Sound.Addison-Wesly. 1982, pp.52-53.转引自韩宝强《音的历程—现代音乐声学导论》,人民音乐出版社,2016年,第129—130页。。(4)马大猷、沈㠙提出的开管校正量为1.7d,闭口校正量1.4d(d为管的直径)①马大猷、沈㠙:《声学手册》,科学出版社,1986年,第808—809页。;在胡企平、夏季、刘存侠的研究中,均认为1.7d的开管校正量是可信的。②分别见胡企平:《中国传统管律文化通论》,上海音乐出版社,2003年,第209页;夏季:《中国古代早期管乐器及黄钟律管研究》,中国科学技术大学2006年博士论文,第46页;刘存侠:《朱载堉异径管律的理论研究》,《中央音乐学院学报》2006年第1期。(5)王光祈曾做过实验,得出长度23公分,内径0.9公分的铜律管在15°时,闭管校正值为1.5公分。③王光祈:《中国音乐史》,音乐出版社,1957年,第52—55页。以此反推管口校正数比值1.5=0.9×5/3,也就是说闭管校正量为5d/3。陈正生曾推算,杨荫浏在《中国音乐史纲》中计算律高所采用的闭管校正量为5d/3。度量衡学者丘光明、邱隆在研究中也使用了5d/3④分别见丘光明、邱隆、杨平:《中国科学技术史·度量衡卷》,科学出版社,2001年,第47页。丘光明:《中国历代度量衡考》,科学出版社,1992年,第2页。但均未标明公式来源。。(6)徐飞认为闭管校正值为1.6667D(D为直径,5d/3≈1.6667d),而开管为0.306D,但计算时,由于两端均有管口校正,要取2×0.306D=0.612D⑤徐飞:《黄钟律管管口校正考》,《中央音乐学院学报》1996年第3期。。陈正生运用公式的检测验证闭管律管,5d/3的管口校正值是可信的⑥陈正生:《黄钟正律析》,《艺苑》1989年第2期。,但开管的管口校正量0.306D远远小于闭管的校正量,这显然是不正确的⑦陈正生:《谈谈开管律管与闭管律管频率计算公式—与徐飞同志商榷》,《中国音乐》1997年第1期。。在律管实证研究的基础上,陈正生强调5d/3或0.6r(r为半径)这两个量只是律管和笛管管口校正量中的特例。5d/3这一管口校正量,只有用正确的吹律方法,吹奏两端管径完全相等的闭管律管时才具有的管端校正量,而且只适用于同径管,不适用于异径管,管径差越大,误差越明显;0.6r(即0.3d)乃是两端管径完全相同之管的末端校正量。⑧陈正生:《我国历代管口校正研究述评》,《交响》(西安音乐学院学报)1997年第3期。(7)吴南薰引用的物理学家瑞利的闭管管口校数为2.7R(R为半径)⑨吴南薰:《律学会通》,科学出版社,1964年,第397页。。但戴念祖所引用的瑞利的吹口校正数为5d/3,而开口校正数为0.29D⑩James Jeans, Science and Music. Dover 1986, pp.137—139. 转引自戴念祖《朱载堉—明代的科学和艺术巨星》,人民出版社,1986年,第98页。在闭吹状态下,吹口校正数即闭管校正数。。(8)陈奇猷将开闭管的管口校正数均设为3.3r(r为半径),隗芾也采用同样的公式⑪分别见陈奇猷:《黄钟管长考》,《中华文史论丛第一辑》,中华书局,1962年,第185—189页;隗芾:《隋至宋乐律递变考(上)》,《社会科学战线》1985年第1期。。(9)刘勇、张谦在对顶端不开豁口的律管测音后,推算闭管校正量约等于0.9d,开管约等于1.45d⑫刘勇、张谦:《关于管口校正量的一个实验》,《中国音乐学》1993年第4期。。(10)唐林认为对简单的圆柱形管,闭口管校正值为0.425d,开口管为0.306d⑬唐林、张永德、陶纯孝:《音乐物理学导论》,中国科学技术大学出版社,1991年,第107—108页。。将以上管口校正数统一以管内直径(d)换算后,整理为表1以代入公式计算并与实验数据进行比较。

表1 闭管、开管管口校正数统计
二、开管管口校正数的验证思路
需要注意的是一个似乎人所共知却常被忽略的重要问题:随着温度的升高,声波在空气中传播速度加快,多次吹奏后,随着管内温度的上升,管乐器发音会越来越高。陈奇猷《黄钟管长考》设0℃音速为33200毫米/秒带入温度变化系数0.003665,代入15℃起算(N表示频率,L为管长,t为温度,a为管口校正数3.3,A=1+0.003665)①陈奇猷:《黄钟管长考》,第185—189页。,虽文中并未说明音速与温度系数及管口校正数的来源,却启发了笔者对这一问题的思考。此前,尽管学者们或多或少均提及温度影响,但计算时,一般以标准大气压下15℃的声速440m/s为默认值。事实上,温度的影响是管律研究中不可忽略的一个变量。周林生、陈正生认为气温每±1℃,笛箫的音高随之±3音分②见周林生《笛箫的温差与音差》,《乐器》1989年第4期;陈正生《也谈温差对笛箫频率的影响》,《乐器》1990年第3期。。笛箫演奏与研究专家赵松庭认为:“温度±10℃,将使一定管长的频率升高或降低1/6—1/7个音(笔者注:约30音分),对于有训练的耳朵来说,这是一个不能忍受的误差。……据实际经验,得出管内的实际温度可近似地列为1/3(36℃-大气温度)+大气温度。现将管内温度设为t0,气温设为t,则温度变量可用表示(公式①)。”③赵松庭:《温度与乐器音准问题》,《乐器科技》1978年第1期。这一公式反映了笛箫在演奏时的温度变化情况,但律管并非演奏乐器,形制也有差异,这个公式是否仍适用?温度与律高的规律如何?这需要我们用实验来推导和验证。
学界公认0℃、15℃、25℃空气中声速分别为331m/s、340m/s、346m/s。一般认为声音速度与温度间的关系可简略地表达为v=331.5+0.61t(公式②,0℃声速约为331.5m/s,t为环境温度)。2007年,新疆大学物理科学与技术学院研究团队使用超声波发生器,测量空气中声速与环境温度关系的新公式计算结果与之相符合(相差1米以内):“在室温下,干燥空气中的声速公式为,其中v0表示0℃时音速331450mm/s,t为环境温度。”④买买提热夏提·买买提、亚森江·吾普尔、复尔开提·夏尔丁:《简谈空气中的声速与温度关系》,《物理实验》2007年第11期。(公式③)笔者将0~36℃环境温度分别代入公式②和③进行计算,声速最大差距仅为0.84米,但新疆大学的结果更接近0℃、15℃、25℃下的默认声速⑤15℃、25℃、36℃时按公式②计算为340.6米/秒、346.75米/秒、353.46米/秒;按公式③计算为340.43米 /秒、346.28米 /秒、352.62米 /秒。温度越高,二者差距越大。,因此,将之用于本文的声速计算(见附录)。验证方式如下:
首先推算不同管口校正数的理论音高,即将温度代入声速公式③:算出实时环境声速V(见附录),再将V值和以上所统计的9种管口校正数分别代入开口管频率公式④(k为管口校正数)计算音高。将计算音高与律管实测音高比较后,找出最符合实测的管口校正数。此外,将环境温度代入赵松庭的管内温度公式①,可推算管内温度,再代入公式③和④,得到的音高就可以用于检验公式①(t0为管内温度,t为气温)的适用性。
管乐器的发音特点是“声无定高”。即便是同一人在完全不改变角度、位置条件下吹奏的同一个长音,也会随着吹气对管内温度的增加而逐渐升高。因而,我们采用“音高区间”的统计方式,即从每次实验的测音样本中,分别选取吹律人吹奏的最高值和最低值构成实测的音高区间,作为验证管口校正数的参照。⑥限于篇幅,实验二、三中仅列音高区间,处于区间内的样音不再一一列出。以下实验历时数月,是以同一套律管在不同温度条件下的多次测音与理论推算为基础进行统计与计算。
三、开管管口校正数及计温公式的相关实验
1.实验一:18℃时开管吹律实验
本次实验所用的18支历代黄钟律管,形制数据依据文献记载和历代尺制变化来推导①推导过程另有专文讨论,此处不赘。。由泉州市比邻三维科技有限公司使用上海联泰科技3D打印机(精度±0.1mm),光敏树脂材料,制作壁厚2mm的18支顶端不开豁口的律管。用电子数显卡尺(精度±0.02mm/0.001″)测量长度、内径。实验步骤:①吹律人不遮蔽律管底端开管吹奏,竖直持管,口唇遮蔽管口1/2并保持统一②经实验,开管吹律时完全不遮蔽管口很难发声,在内径13mm以下的律管上遮蔽1/2管口较易成声,振动较充分,但遮蔽超过1/2会使音偏低。。每次吹奏前报清律管名称、编号、材料。②全部吹奏过程同步进行录音采样、视频录制。③选取录音数据中的有效样音进行测音。④对所测样音数据进行音高频谱分析。
2020年10月15日,在中国音乐学院半消声声学实验室(本底噪声:22dB),室内温度18℃下,在刘勇教授的指导和监听下,我们进行了黄钟律管的首轮吹律实验,吹律人是史凯敏、赵越。③吹律人赵越:雅乐传习所指导教师。录音及监控:中国音乐学院图书馆技术部负责人,音乐声学硕士罗时欢 (录音设备:麦克风:DPA 4015,声卡:RME Fireface UC,工作站:Pro Tools HD,采样率/采样精度:48kHz/24bitt,录像设备:SONY数码摄录一体机)。测音员:中国音乐学院音乐声学硕士程馨瑶。测音软件GMAS2.0。后面实验中方法一致处不再重述。由于开管竖吹的律管吹奏方式,并非箫笛演奏员日常习惯的奏法,吹律人对此演奏法所要求的气息与口型起初并不熟练,成声率较低。在吹奏时,前段多为气流声,往往在中后段才发出有效音,我们在不能选出有效整段发音的情况下,退而选择截取这部分发音的稳定部分作为测量样本。取音标准是:①听觉上有明显音高;②音准比较稳定;③在视觉上,呈现出的波形较为稳定,振幅较大。结合测音员和助手的主观耳测,每支律管取出2~3个质量最好的有效样音。
音准判断标准:由于“大多数音乐家的同一性音准感具有±10音分的宽容度,多数音乐家的和声性音准感具有-38至+14音分的宽容性”④韩宝强:《音的历程—现代音乐声学导论》,第31页。,因此,本文判断±10音分以内为音高一致;±10~22音分以内为音高基本一致;±22~33音分为音高略有差异;±33~50音分为中立音。
两位吹奏人气息、嘴劲儿、口风等必有一定差异,但从吹律统计结果看,发音是比较稳定的,上下浮动音高区间在30音分以内,不影响律位的确定。从9种管口校正数分别代入18℃环境声速342197mm/s(见附录)的计算结果看,代入0.29d~1d管校数的计算结果全部偏离实测区间,因而首先排除;代入1.45d管校数仅有5个样本处于实测区间;代入1.65d有13个样本处于实测区间,占72.2%;只有1.7d和5d/3(约1.66667d)管校数的计算结果,始终处于“实测音高区间”以内,最符合实测音高。笔者将1.7d与5d/3管校的计算音高分别与最高吹奏音高相比较,计算偏离最高吹奏音的音分值(“偏离音分”中负值表示低于最高吹奏音高的音分数),二者的差数只有2音分(表2),可以忽略不计,1.7d可视为5d/3的约数。
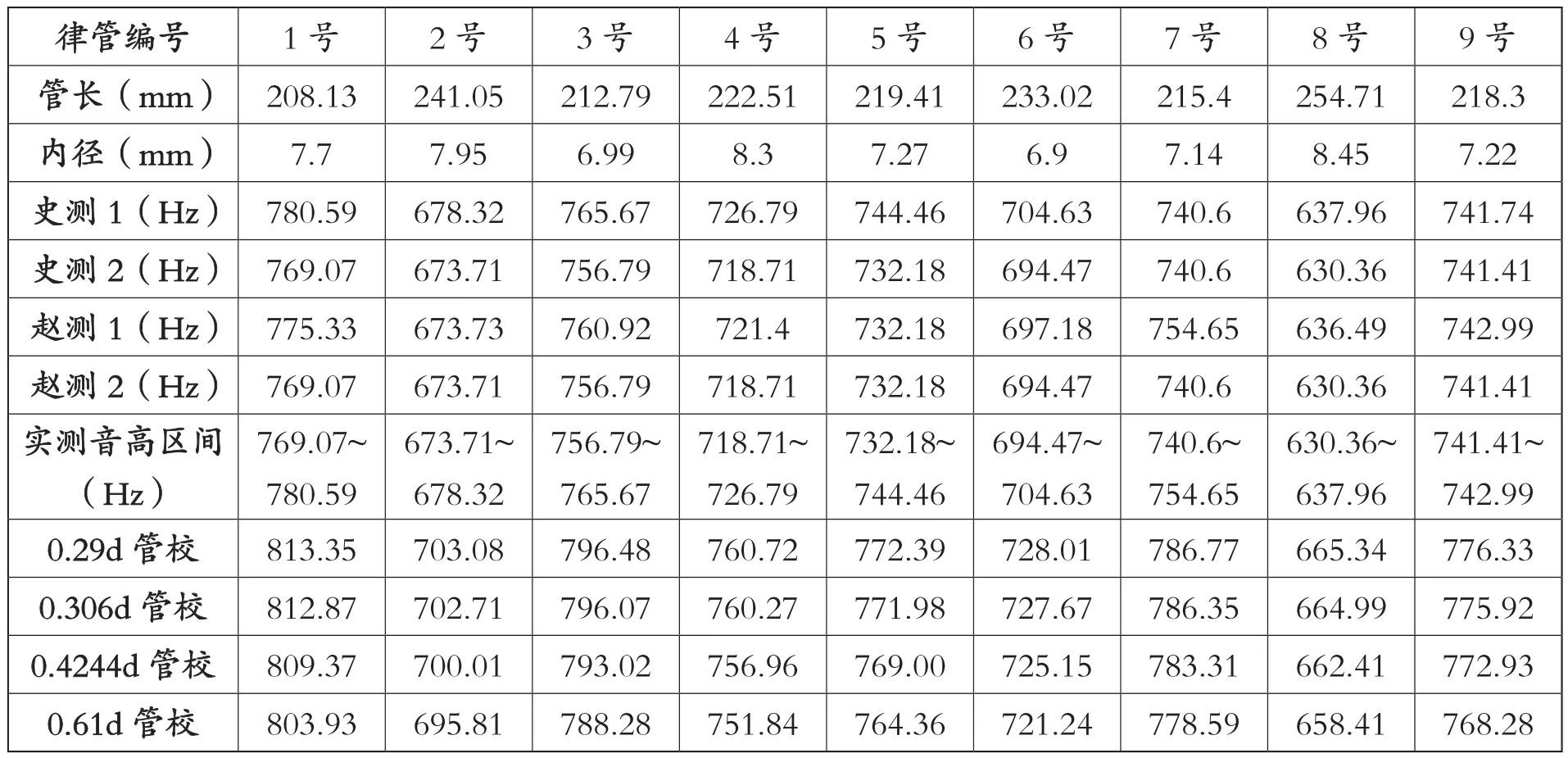
表2 18℃开管测音与9种管校数计算音高(单位Hz)比较表

(续表)
2.实验二:8℃开管吹律实验:
2021年1月16日上午11:00,在亳州学院音乐系5楼回廊,环境温度8℃时,笔者进行了第二轮吹律实验。古代灵台定律是在冬夏二至的正午,尽管很难确定古代精确的温度情况,但以现代气候作为参照,应相去不远。我们查询了近五年来开封、西安和北京的二至气温情况,亳州当日气温是-4°~4℃,放寒假时的校园十分安静,我们使用电子温度仪在窗口测得温度为7℃,关闭回廊门窗后,温度稳定在8℃,与中原冬至正午的平均气温大致相符。按照律管编号,在摄像机全程记录下,笔者依次开管竖吹1~18号黄钟律管。

表3 冬至、夏至气温统计表(单位:摄氏度℃)
实验结果:
在8℃的环境声速336269mm/s下,1.45d管校的计算结果,更符合实测音高,偏离值最大13.8音分。而5d/3管校计算值偏离则明显偏大(表4),理论上,在角度、气流速度稳定的情况下,管口和末端溢出气流的长度应该是固定的,这一变化,应该是由于管内温度高于环境温度,管内声速大于环境声速的而产生的。陈正生先生曾按照每±1℃,声速加减0.61米,多次验证发现“计算出的频率难同吹出的音高相合”,认为“律管中的声速不该简单地运用大气声速”①陈正生:《“黄锺正律”析—兼议律管频率公式中的物理量》,《南京艺术学院学报(音乐与表演版)》1989年第2期。。因而,有必要找出适合的管内速度计算公式来。

表4 8℃开管测音与计算音高比较表
赵松庭先生曾提出过管内温度的公式:管内的实际温度=1/3(36℃-大气温度)+大气温度,算出8℃时,管内温度为17℃,声速约为341609mm/s,代入5d/3管校数的计算值已经全部超出实际吹奏的音高浮动区间(见表5),这说明代入的声音速度过高,管内温度并没有达到17度。于是,笔者按照附录中的计算声速,在EXCEL中从8℃开始逐一替换公式中的速度,当代入12℃的声速338653mm/s后,这一偏离值与实测“吹奏音高浮动区间”已经极为贴近(见表5“12℃,5d/3管校”一栏)。看来,律管上,管内温度的变化幅度没有笛箫上大。

表5 赵松庭管内温度公式验证表
首先,呼出气体的温度并非36℃。陈振华医生曾用“德国耶格公司Master-Screen肺通气功能检测系统”观察哮喘儿童呼出气温度(EBT)的变化,正常为(33.3±0.3)℃②陈振华:《呼出气温度在儿童哮喘急性发作时及发作后的监测意义》,《实用临床医药杂志》2020年第19期。。因而笔者首先将赵先生公式中表示体温的36替换为33,并尝试将1/3的比值替换为1/4、1/5、1/6、1/7……进行验算,当管内的实际温度=1/7(笔者按:呼气温度+6倍大气温度),即t0=(6t+33)/7(公式⑤)时,算出的温度改变值与实验相符合(见附录)。如果温度改变,这个公式是否仍与实践相符?于是,接下来我们进行了23℃环境下的测音实验(表6)。

表6 23℃ 开管测音与计算音高比较表
3.实验三:23℃开管吹律实验
2021年1月17日下午,在亳州学院音乐系500工作室,环境温度23℃时,笔者用同样的方法与步骤再次进行了第三轮实验。
实验结果分析:
1.按照t0=(6t+33)/7计算出23℃环境下,管内温度为24℃,将管内声速345706mm/s代入公式④,算得每升高1℃,音高升高2.9音分。同时,计算值与测音音高区间基本符合(表6)。
2.代入23℃的环境声速345123mm/s与代入345706mm/s管内声速的计算值极为相近。原因是,在18℃以上,管内温度与外界温差在2℃以内,这意味着,体温对管内的加温作用在6音分以内,人耳难以分辨,越接近33℃,这一影响越小;在33℃以上,管内温度低于外界温度,原则上,会拉低音高,但40℃以下,这个影响不超过1℃也可以不用考虑。换言之,在19℃~40℃,可以用空气速度与5d/3的管口校正值来计算音高。但在19℃以下,管内温差的影响会越来越大,有必要使用管内声速(见附录)来推算音高。
3.从三次对同一套律管的测音来看,温度对音高的影响是确定音高必须计入的一个变量。计算8~23℃是升高15℃的音高差(表7简称音差),8~18℃是升高10℃的音高差,据此,可算出每升高1℃,约发生1~3.3音分的变化,平均后最大为2.91音分,符合公式⑤的推算。
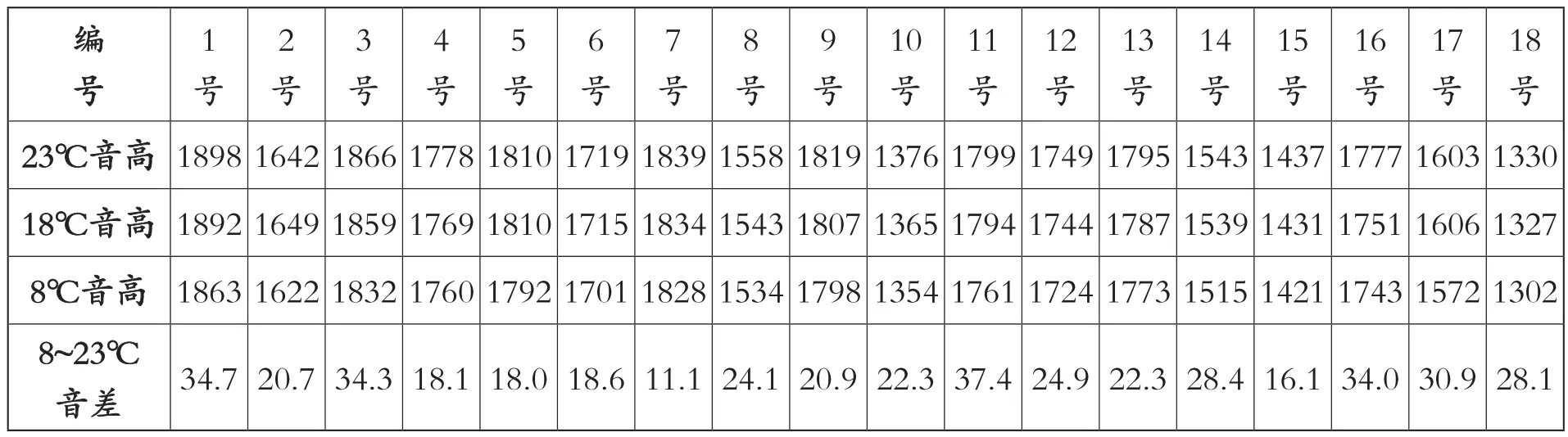
表7 三次黄钟律实测音高对比表(单位:音分)
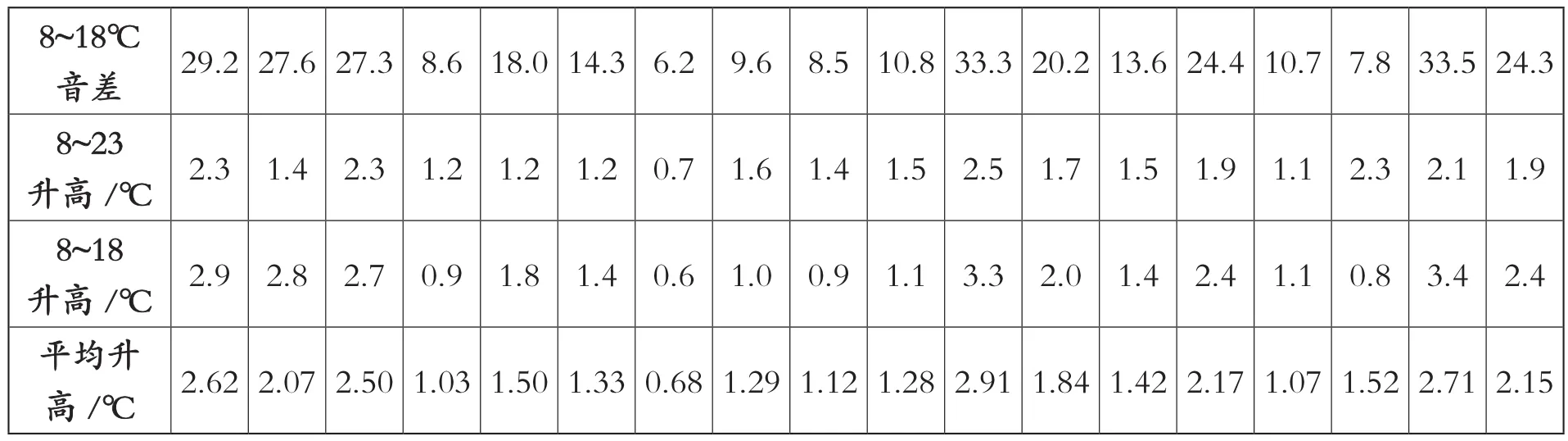
(续表)
从以上三次不同温度环境下对同一套黄钟律管的测音,可以看到,在计入管内温度影响后,使用5d/3的开管管口校正数可以得出基本符合吹奏区间的理论音高(计算音高与实测偏差在20音分以内),这证明在开管吹律的情况下,管内温度t0=(6t+33)/7(公式⑤,t表示环境温度)是可以成立的。在19°以上,是否使用这一公式对音高计算影响很小(6音分以内),可直接用空气温度计算,但低于此温度时,不代入管内温度,则计算值会偏低于实测音高较多。为简化计算步骤,可将公式⑤代入(其中v0表示0℃时音速331450mm/s,t为管内温度),可得管内速度公式为:,接着代入公式④,则计温开管音高公式可推算为(F为音高频率,k为管口校正数5/3。l表示管长,d是管内径,t为气温)。这个公式将计算管内温度、管内速度、音高的三个步骤合而为一,使音高与气温直接关联。
四、其他实验样本对公式有效性的验证:
为检验公式的有效性,于2021年1月20号,室温15℃时,对3D树脂打印的一组同形管①同形管指长径比相同的律管。表8中的律管长径比全部为26∶1。再次开管竖吹测音,并与此前在2020年11月15号18℃环境温度下对这组律管的测音音高加以比对,发现很难得出温度变化与音高具体变化的数值,因为吹律人的状态不可能完全一致,尤其是11号管以下,管口小于7mm,吹奏难度和口风的影响也越来越大。但总体上看,温度对于音高的作用是很明显的,仅有1例外,其余升高10.02~30.37音分不等,理论计算音高与吹奏测音音高大部分都是符合的。按理论值推算音高改变为7.6音分。
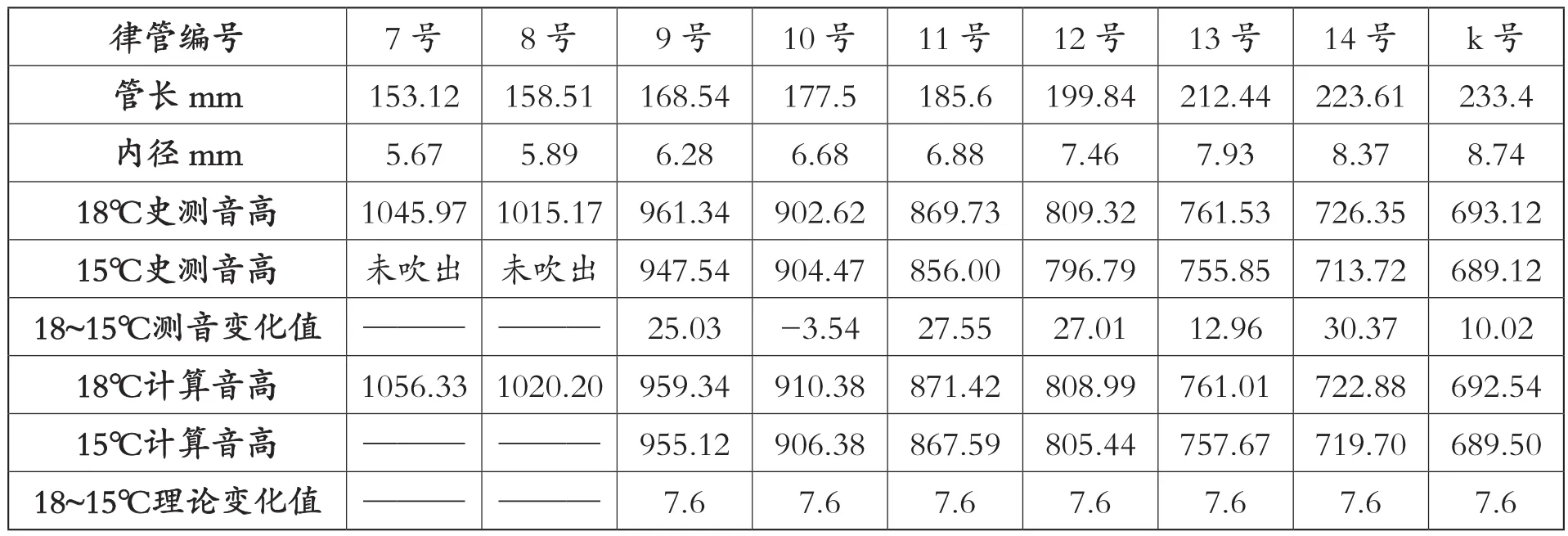
表8 18~15℃同形异径无豁口律管吹奏测音与理论计算比对表
我们还与2020年11月25日在中国音乐学院声学实验室对一组不锈钢无豁口律管的测音结果进行了比对(表9)。13℃环境下,管内温度为15.9℃,算出管内声速为340936mm/s。在管径超过13mm的1A和2A管上,吹奏音高明显偏低于公式的计算。这是由于管径过粗,口唇必须保持在气流可以抵达边楞的位置—遮蔽管口2/3甚至更多,才能有效发声。遮蔽管口越多,偏低于理论计算值就会越大。而在内径小于13mm,长径比大于23:1的3A~5A管上,实测与计算音高是可以吻合的,尤其是长径比越大的管上,不同吹律人(赵越、史凯敏)间的吹奏差异也越小,越趋近于计算值。
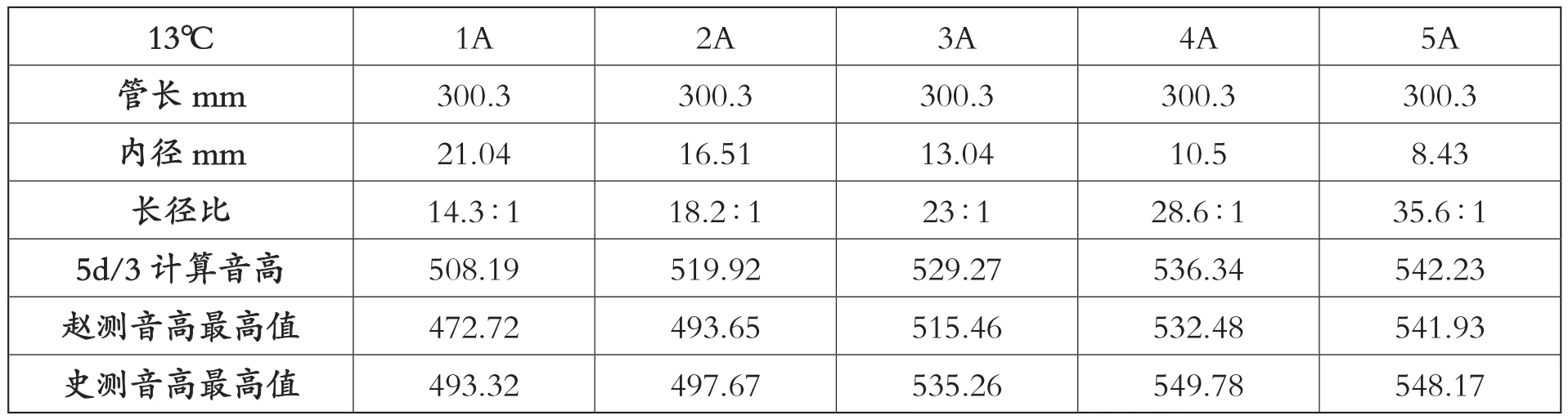
表9 同长异径无豁口不锈钢律管A组测音与理论计算比对表
1991年刘勇先生复原制作的带豁口铜制朱载堉律管,用开管竖吹测音,其中黄钟律管长254.9mm,内径8.96mm,在21℃时,测得开管吹奏音高分别为e2-29、e2-18、e2-37①刘勇:《朱载堉异径管律的测音研究》,《中国音乐学》1992年第4期。。将21℃的温度和管长、内径代入本文推定的计温开管音高公式,计算结果为637.35Hz,合341音分。经实验验证律管上宽、深均为4.5mm的豁口会造成音高升高30~43音分左右②实验过程见史凯敏《中国古代律管造型的衍变—兼谈豁口作用》,《中国音乐》2022年第4期。,如果加上豁口值,理论音高为371~384音分,即e2-16到e2-29,与实测结果高度吻合。
1996年胡企平先生复原制作的康熙铜律管,在15℃室温下,开管竖吹管长233.28mm,内直径8.768mm,不开豁口黄钟律管音高为f2-34③胡企平:《中国传统管律文化通论》,第198—199页。(685Hz)。与本文公式推算值687.67Hz仅差6.7音分。内径8.768mm,管长103.68mm,不开豁口的半太簇管音高测为♯f3-35④胡企平:《中国传统管律文化通论》,第195—199页。(1450Hz),与公式推算值1445.33Hz仅差5.5音分,二者高度吻合。
结论
通过对同一组律管在不同温度下的3次开管吹律测音实验,我们检验了学界常用的9种开管管口校正数的音高推算值,发现直接使用该温度下的空气声速计算时,没有一种管口校正数能全部符合三种温度下的测音结果。只有在计入管内温度的影响算出管内声速(见附录)后,以5d/3的开管管口校正值进行音高计算的结果才与实测的音高区间最为符合。这一系列推算过程可精炼地简化为一个开管计温音高公式:。我们及其他学者更多的律管测音结果也验证了使用这一公式进行律管音高的推算,可以得出与实际吹奏音高符合的结果。可以说,在一定程度上解决了气温对律管音高影响难以估算的问题,提升了管律律高计算的准确性。但需要说明的是,管律研究的复杂性在于实际吹奏的音高除温度外,还受到吹气角度、气流速度、口唇遮蔽管口的幅度的影响,本文所使用的实验及验证的样本全部为长径比在26∶1以上,内径在11mm以下的无豁口的黄钟律管,这种形制比例下,对气流角度和速度的要求很高,变化幅度较小。但在长径比小于20∶1,内径更大的律管上,口唇位置变化导致的音高变化已超过小二度,这将使公式的计算值与实测值的差异加大。这也是目前所有管律声学公式均未能完全解决的一个问题,也说明对于管律的研究仅靠数理推算有其自身的局限性,还需配合制管验声,算验相合,方获真知。

