基于移动群智感知的多旋翼无人机噪声控制技术

杨 倩，王艳娥，梁 艳，司海峰

(西安思源学院 理工学院，西安 710038)

0 引言

移动群智感知是一种新型的数据信息感知作用机制，它利用广泛存在的智能传感设备对采集到的感知数据进行处理。移动群智感知系统具有部署成本低、运行速率快、感知准确性高、覆盖面积大等多项应用优势。常规的移动群智感知系统同时包含数据采集者、任务发布者、网络服务平台三类结构[1]。其中，数据采集者负责接收已发布的任务指令，并根据服务需求收集待处理感知数据，以供服务平台主机的调取与利用；任务发布者负责在网络服务平台中发布执行任务，并可以按照具体实践情况，修改已发布任务的执行进程[2]；网络服务平台作为数据采集者与任务发布者之间的过渡结构，负责对感知数据进行处理，并可以借助传输信道，将这些信息文件反馈给执行主机。

多旋翼无人机是具有三个或三个以上独立旋翼轴的无人驾驶型直升机飞行器，依靠轴电动机的转动带动独立旋翼进行旋转，从而产生向上的升推力。由于旋翼轴间距始终固定，所以改变旋翼之间的相对转速水平，就可以改变轴向推进力的数值大小，进而调节无人机飞行器的实际运行轨迹[3]。在多旋翼无人机运动过程中，蒙皮结构、加筋板结构、典型壁板结构内部噪声信号的布局形式总是保持不断变化的状态，易使噪声信号波动幅值持续增大，对多旋翼无人机的稳定运动能力造成影响。传统模糊逻辑控制方法采用一种模型概率的非线性映射处理方法实时筛选模型子集，剔除无用模型，增加有用模型的权重，并通过模糊推理机制自动调整过程噪声水平，以此实现噪声控制。但是在该方法应用后，多旋翼无人机噪声幅值依旧保持在较高水平，实际应用效果并不好[4]。为解决上述问题，以移动群智感知作用机制为基础，设计一种新型的多旋翼无人机噪声控制方法。

1 噪声信号布局分析

由于多旋翼无人机噪声信号的传输行为规律性不明显，为了更好地获取噪声信号位置，还应分析信号参量在蒙皮结构、加筋板结构、典型壁板结构内的布局形式。

1.1 无人机蒙皮结构

多旋翼无人机蒙皮结构(如图1所示)是一块完整的薄板，其外表面为独立绝缘层(图1中的虚线框架)，因此不具备传导噪声信号的能力，故而噪声信号传导行为只发生在蒙皮结构内表面(图1中的实线框架)[5]。考虑到移动群智感知机制对噪声信号传输行为的影响，规定由左至右的方向为信号传输正方向，且整个无人机蒙皮结构内部不存在噪声信号的负向传输行为。

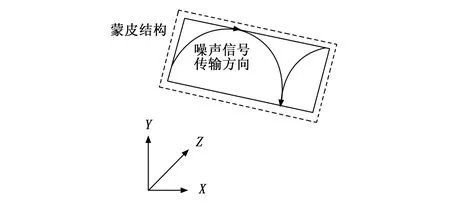
图1 蒙皮结构内的噪声信号布局

若多旋翼无人机的行进运动方向发生改变，则X、Y、Z三个空间坐标轴的定义方向也会随着出现变化，为避免噪声信号在蒙皮结构内的传输方向发生改变，默认在运动过程中，只有独立绝缘层的存在方向会出现变化，而内表面存在方向始终保持不变[6]。

1.2 无人机加筋板结构

如图2所示,多旋翼无人机加筋板结构包含完整的蒙皮结构和两根平行筋条，可以在维持噪声信号正向传输行为的同时，避免噪声波幅值出现明显增大的变化，一方面为无人机飞行器提供一个相对稳定的运动环境，另一方面也可以将蒙皮结构内暂存的噪声信号提取出来，使得主机元件可对这些信号参量进行按需分配与处理[7-8]。

图2 加筋板结构内的噪声信号布局

在实际传输过程中，加筋板结构内噪声信号传输正方向与X坐标轴、Y坐标轴、Z坐标轴之间的夹角数值完全相等。

1.3 无人机典型壁板结构

如图3所示,多旋翼无人机典型壁板结构采取平行筋条并列连接的方式，可以将整个蒙皮结构分割成多个完全独立的空间，从而使得噪声信号在传输过程中的波长值水平能够得到有效控制[9]。典型壁板结构内部的噪声信号始终保持首尾交替相连的传输形式，随着信号传输时间的延迟，其波动幅值水平则呈现出不断下降的变化状态。

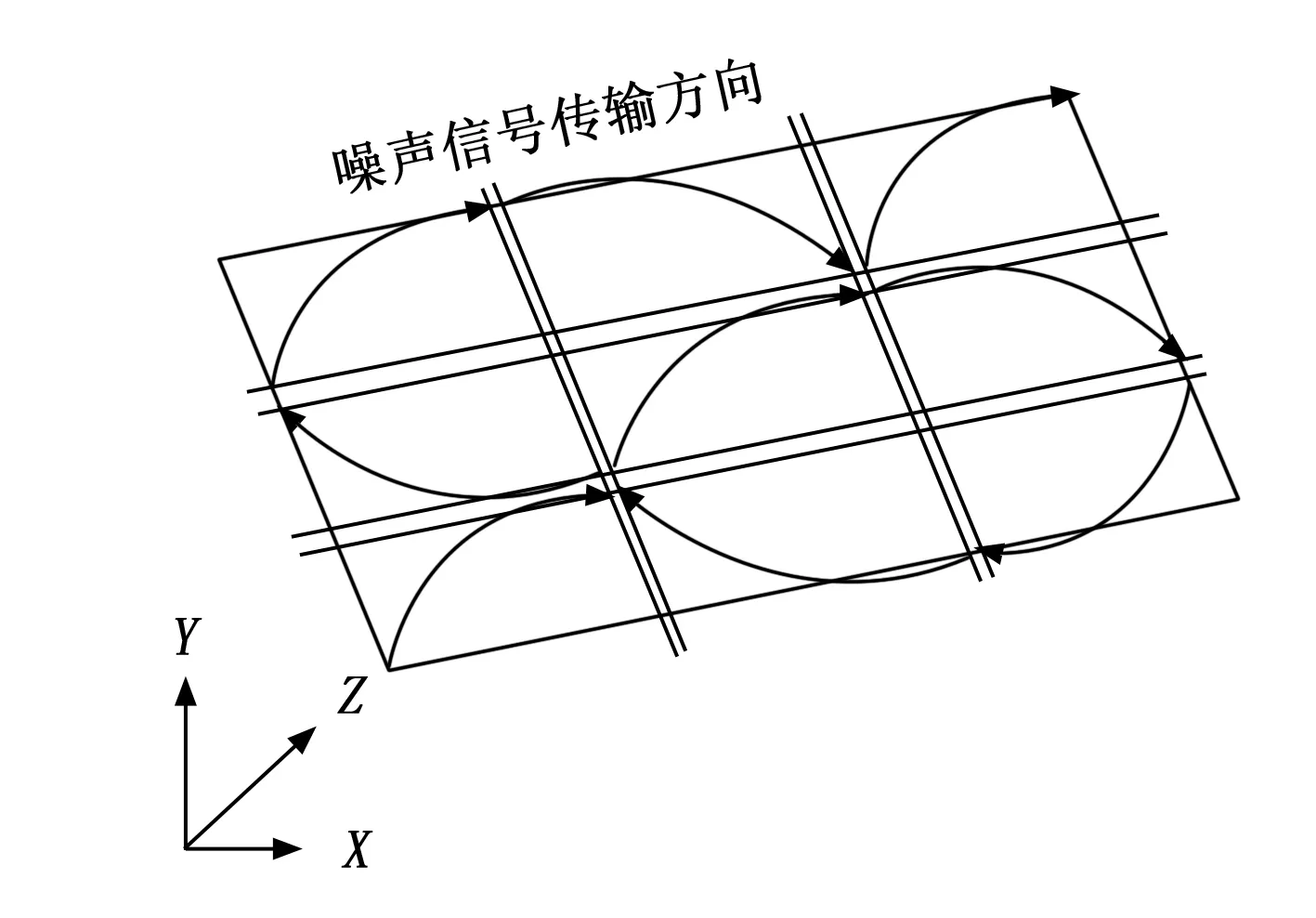
图3 典型壁板结构内的噪声信号布局

为实现对多旋翼无人机噪声信号的准确控制，信号参量在典型壁板结构第一个独立空间与最后一个独立空间内的传输方向必须保持一致[10]。

在分析多旋翼无人机噪声信号在无人机蒙皮结构、加筋板结构、典型壁板结构内的布局形式为基础上，提取无人机板状结构的振动特性，以期为后续的噪声控制奠定坚实的基础。

1.4 板状结构振动特性

板状结构作为多旋翼无人机的核心组成装置，具有过滤噪声信号的作用。在电感元件的作用下，入射噪声信号波段会经过多次折射，当直接反射输出量与结构元件自身的信号感应能力相匹配时，板状结构对于噪声信号的吸收能力最强，输出噪声信号也就不会对多旋翼无人机的稳定飞行能力造成影响[11-12]。详细的多旋翼无人机噪声信号传播原理如图4所示。

图4 多旋翼无人机噪声信号传播示意图

在移动群智感知机制的作用下，可将板状结构振动特性表达式定义为：

(1)

2 多旋翼无人机噪声控制原理

为实现对多旋翼无人机噪声信号的有效控制，需要根据板状结构的振动特性，研究同步开关阻尼、短路开关阻尼、电感开关阻尼、外加电压源开关阻尼的定义表达式，以此为后续的控制任务调度奠定坚实的基础。

2.1 同步开关阻尼

多旋翼无人机噪声信号的传输能力会因同步开关阻尼行为的变化而发生改变，故而求解同步开关阻尼表达式，能够确定噪声信号在单位波动区间内的幅值水平，从而实现对噪声波动行为的有效控制。同步开关阻尼以同步控制思想作为切入点，可以根据多旋翼无人机噪声信号的波动特征，判断板状结构振动特性的合理性[13]。若将多旋翼无人机板状结构振动特性视为已知条件，则可认为改变同步开关阻尼条件既可以控制噪声信号的传输频率，也能够有效压缩波动幅值。

无人机噪声信号同步开关阻尼定义式为：

(2)

其中:λ1表示噪声信号的振动系数，s1表示振幅基向量，κ1表示噪声信号的波动系数，d1表示波动传输基向量，ι表示波幅参量的初始赋值，lι表示基于系数ι的噪声信号波动特征。对于多旋翼无人机噪声信号而言，同步开关阻尼表达式的计算数值受到板状结构振动特性的直接影响。

2.2 短路开关阻尼

受到移动群智感知机制的影响，在多旋翼无人机行进过程中，噪声信号传输耗能与电能累积量始终保持持平，因此通过局部短路的方式，促使电能累积量持续增大，可以提高噪声信号的传输耗能水平，从而使得主机元件能够准确掌握噪声信号传输行为，并对其进行针对性控制。与同步开关阻尼思想相比，根据短路开关阻尼表达式所制定的噪声控制方法目的性更强，因此其实际控制效果也就更为明显[14-15]。用λ2表示局部短路系数，s2表示噪声信号的具备感应特征，f表示短路情况下的噪声信号累积系数，θ表示直流噪声信号与短路噪声信号的传输交角，cosθ表示角θ的余弦值。

无人机噪声信号短路开关阻尼定义式为：

(3)

由于多旋翼无人机的行进速率始终保持变化状态，所以传输交角数值也不能保持稳定，但其变化范围始终保持在(15°，105°)的数值区间内。

2.3 电感开关阻尼

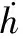
(4)

受到无人机板状结构振动特性的影响，电感开关阻尼表达式的计算取值始终小于同步开关阻尼与短路开关阻尼。

2.4 外加电压源开关阻尼

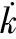
无人机噪声信号外加电压源开关阻尼定义式为：

(5)

为控制外加电压源开关阻尼表达式取值为负，要求s4系数的取值也必须小于“0”。

根据同步开关阻尼、短路开关阻尼、电感开关阻尼与外加电压源开关阻尼计算结果，构建多旋翼无人机噪声控制模型，该模型的具体描述如下：

W=KP(w1a1-w2a2)+KIw3a3+KDw4a4

(6)

其中:KP、KI、KD分别表示PID控制器不同的参数，w1、w2、w3、w4分别表示同步开关阻尼、短路开关阻尼、电感开关阻尼与外加电压源开关阻尼权重。

3 基于移动群智感知的噪声控制任务调度

为实现对多旋翼无人机噪声的有效控制，应综合考虑同步开关阻尼、短路开关阻尼、电感开关阻尼与外加电压源开关阻尼计算结果，生成多旋翼无人机噪声控制任务，利用移动群智感知对噪声控制任务进行调度，保证噪声控制质量与效率。移动群智感知算法的作用下，无人机噪声控制任务的调度处理由群节点定义、感知任务分配、调度性能指标计算三个环节共同组成，本节将针对上述内容展开研究。

3.1 群节点定义

在移动群智感知机制中，群节点部署形式与待调度任务指令的排列形式完全一致，一般来说，除去输入节点“0”、输出节点“e”之外，整个树状群节点组织(如图5所示)至少还需包含三个层级连接结构。“0”输入节点与第一层节点群组相连，前者负责接收主机元件输出的调度任务执行指令，后者负责分类储存这些数据信息参量；第一层节点群组与第二层节点群组相连，两者共同组成了树状群节点组织的中间过渡结构[20-21]；第三层节点群组的个数值是第二层节点群组的二倍，两者相结合能够准确描述出任务调度指令所处的实际执行状态；“e” 输出节点存在于树状群节点组织的最末端，可以根据移动群智感知机制的作用形式，对任务调度指令数据进行重排处理。

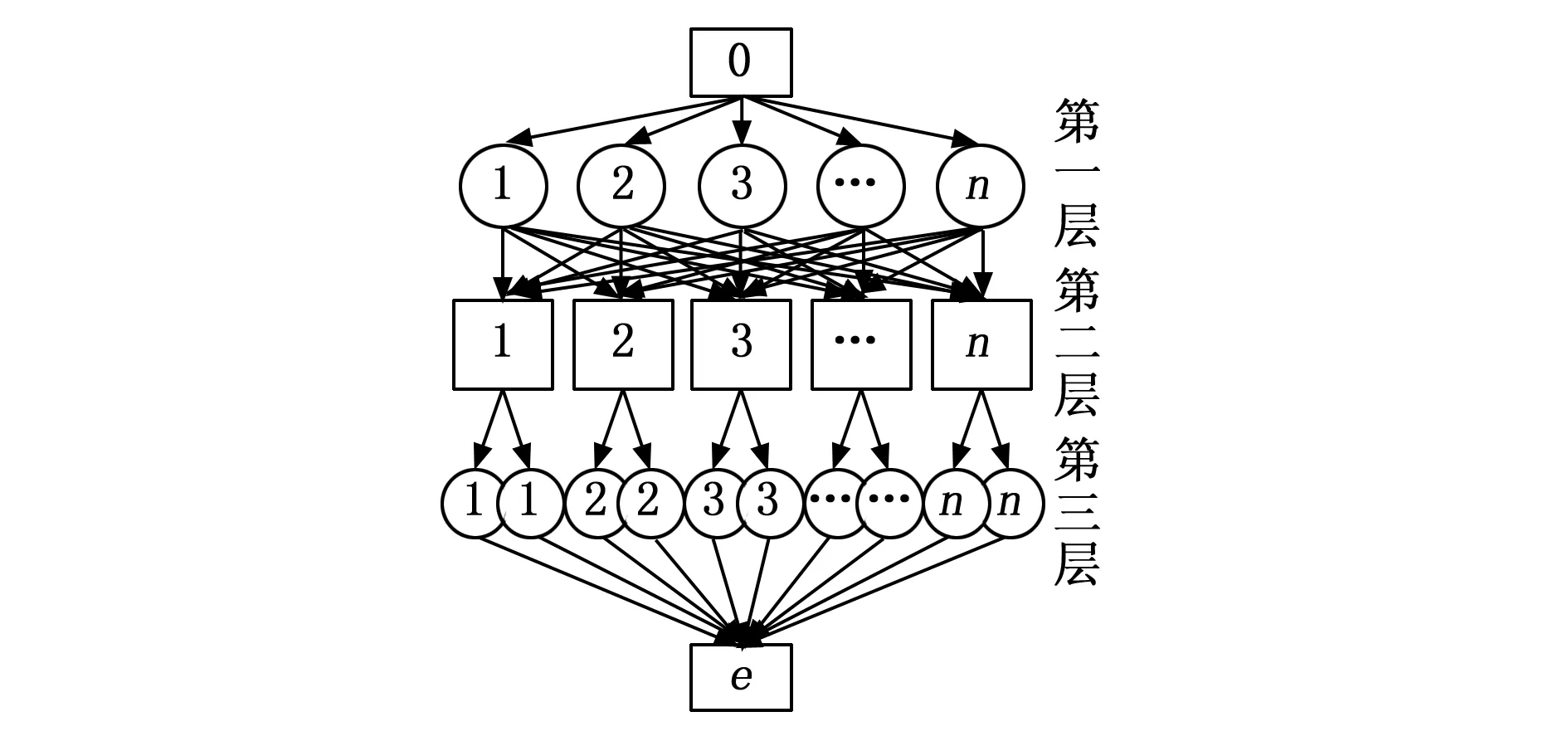
图5 移动群智感知节点部署

α表示过渡节点个数的初始值，n表示系数α的最大取值，qo表示“0”输入节点编码系数，qe表示“e”输出节点编码系数，χ0表示系数qo的译码特征，χe表示系数qe的译码特征。联立上述物理量，得到移动群智感知机制的群节点定义条件W如下：

(7)

为保证树状群节点组织的稳定性，要求系数n的取值必须大于已连接层级结构的个数值。

3.2 感知任务分配

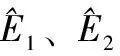
(8)

在移动群智感知机制的认知中，只有扩大感知任务分配条件对于数据信息参量的容纳能力，才能实现对多旋翼无人机噪声信号传输行为的有效控制。

3.3 调度性能指标

对于多旋翼无人机噪声信号而言，任务调度思想的主要目的就是约束移动群智感知机制的作用能力，由于噪声信号的传输行为与存储形式并不唯一，故而在定义调度性能指标时，要求所选取数据的信息参量必须具有较强的容错性[24-25]。用ε、γ分别表示两个随机选取的调度任务规划向量，且ε≠γ的不等式条件恒成立，uε表示基于向量ε的噪声信号感知系数，uγ表示基于向量γ的噪声信号感知系数，φ表示基于移动群智感知的噪声信号容错参量，φ表示既定的调度任务数据规划残差值，联立公式(8)，可将调度性能指标求解表达式定义为：

(9)

若将多旋翼无人机噪声信号作为唯一的参考变量，则可认为在移动群智感知机制的作用下，联合感知任务分配条件，对调度性能指标进行提取处理，就可以准确定义任务数据信息的实际传输形式，从而避免对单一噪声信号进行重复标记。

通过上述过程实现多旋翼无人机控制任务调度，保证多旋翼无人机噪声控制效果，提升多旋翼无人机工作质量与效率。

4 实例分析

4.1 器材选用

选择Phantom 4 Pro V2.0型多旋翼无人机飞行器作为实验对象。飞行器实物图与实际飞行图如图6与图7所示。

图6 飞行器实物图

图7 实际飞行图

将MicW——i437L传声器放置在所选取的无人机飞行器之上，调节各项飞行示数，使得无人机保持相对稳定的运行状态。表1反映了实验过程中的相关实验参量的设置数值。

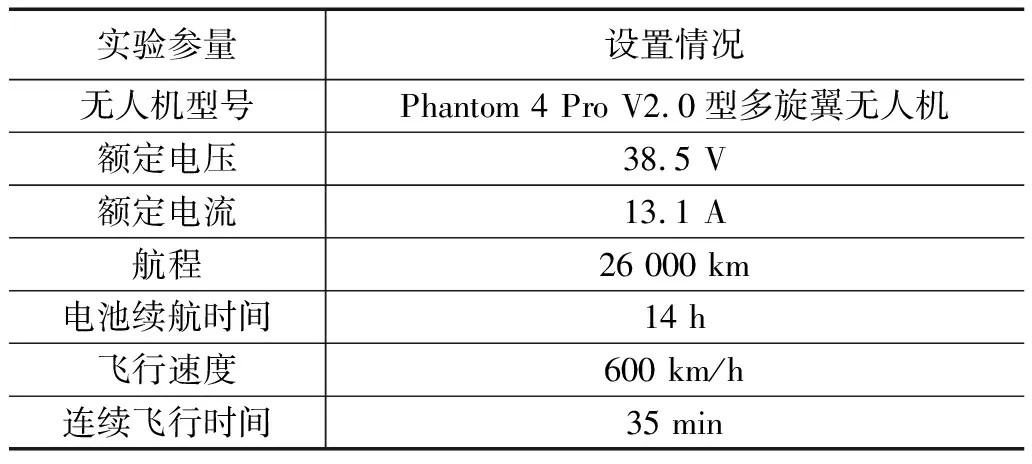
表1 实验参数设置

出于公平性考虑，基于移动群智感知的多旋翼无人机噪声控制技术、模糊逻辑控制方法参量指标数值始终保持一致。

4.2 飞行轨迹规划

通过遥控器设备调节多旋翼无人机的飞行高度，忽略外界风力等干扰性因素的影响，认定无人机飞行器在噪声监测过程中始终保持绝对稳定的运动状态。在飞行场地上选取一个节点作为测量基站，以基站节点为源点，选取固定空间区域作为噪声信号接收区，记录当多旋翼无人机路过该区域时，其噪声波动幅值分别在X轴、Y轴、Z轴方向上的数值变化情况，如图8所示。

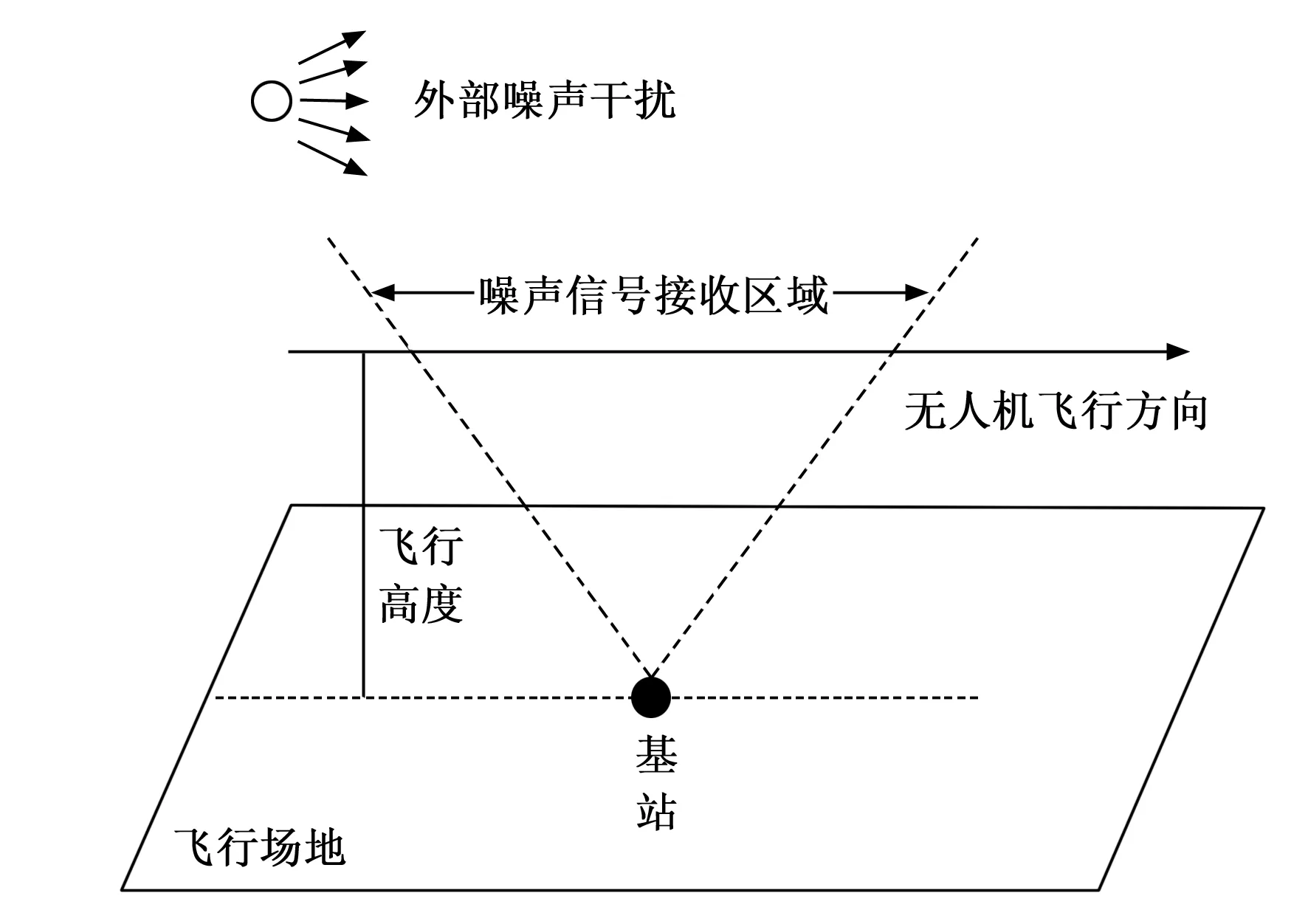
图8 多旋翼无人机的飞行轨迹

由于外部噪声干扰行为的作用方向并不固定，所以测量所得噪声信号波动幅值在X轴、Y轴、Z轴方向上都会出现变化。

4.3 测试案例

存在外部噪声干扰的情况下，基站节点所检测到的无人机噪声信号波动幅值可以用来描述多旋翼无人机飞行器的运动稳定性。一般来说，基站节点所检测到的无人机噪声信号波动幅值越小，就表示多旋翼无人机飞行器的运动稳定性越强；反之，若基站节点所检测到的无人机噪声信号波动幅值相对较大，则表示多旋翼无人机飞行器的运动稳定性也就较弱。

首先，令基站主机按照实验组控制方法检测无人机噪声信号幅值；然后，再令基站主机按照模糊逻辑控制控制方法检测无人机噪声信号幅值；最后，对比实验组、模糊逻辑控制检测数值，总结实验规律。

非干扰情况下的无人机噪声信号幅值如图9所示。

图9 非干扰情况下的无人机噪声信号幅值

分析图9可知，非干扰情况下无人机噪声信号幅值在X轴方向上的均值水平最高、在Z轴方向上的均值水平最低，但明显Z轴方向上噪声信号幅值的数值变化态势更为平稳。

不同方法的无人机噪声信号幅值的实验数值如表2所示。

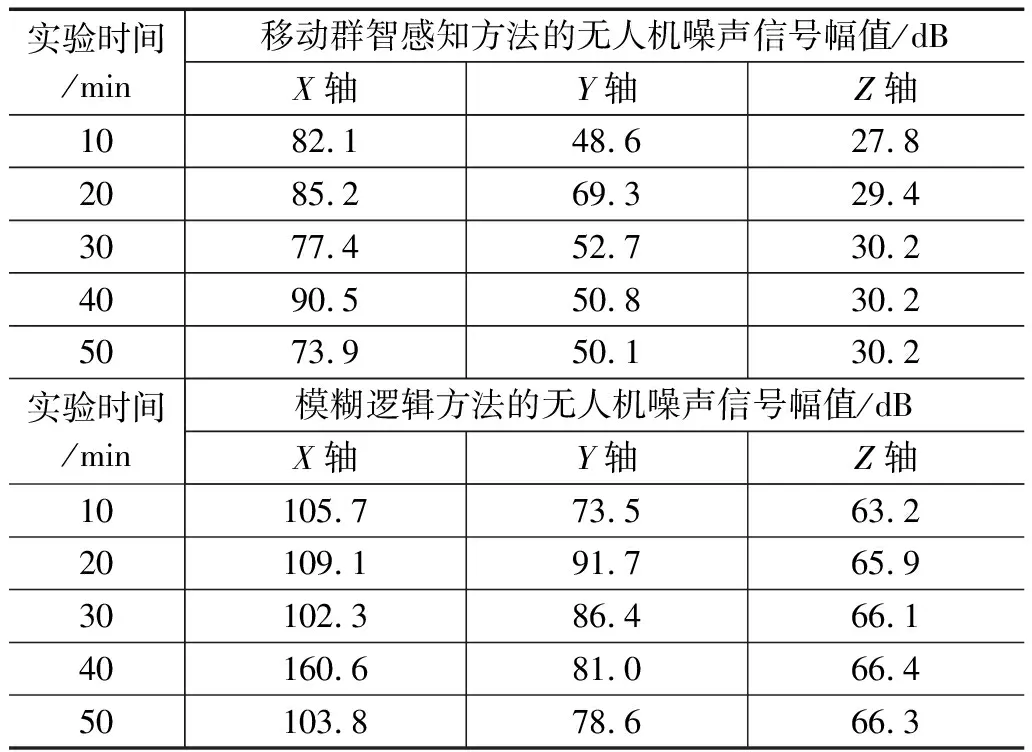
表2 无人机噪声信号幅值的实验数值

实验组：在实验过程中，移动群智感知方法应用后，无人机噪声信号幅值的变化态势始终与非干扰情况下的信号幅值变化态势保持一致，但很明显移动群智感知方法的均值水平更低。实验组X轴最大值90.5 dB、Y轴最大值69.3 dB、Z轴最大值30.2 dB，远小于非干扰情况下的X轴最大值108.3 dB、Y轴最大值88.2 dB、Z轴最大值51.8 dB。

模糊逻辑方法应用后的无人机噪声信号幅值的变化态势也与非干扰情况下的信号幅值变化态势保持一致，但其均值水平却相对较高。模糊逻辑方法的X轴最大值160.6 dB、Y轴最大值91.7 dB、Z轴最大值66.4 dB，高于非干扰情况下的X轴最大值108.3 dB、Y轴最大值88.2 dB、Z轴最大值51.8 dB，更远高于实验组数值水平。

综上可知，本次实验结论为：

1)模糊逻辑控制方法并不能有效控制无人机噪声信号幅值在X轴、Y轴、Z轴方向上的数值水平，在维持多旋翼无人机稳定运动方面的实际应用能力相对较弱；

2)移动群智感知方法在有效控制无人机噪声信号幅值方面的应用能力较强，可以保证X轴、Y轴、Z轴方向上噪声信号波动幅值始终处于较低水平，符合保障多旋翼无人机稳定运动的实际应用需求。

5 结束语

与模糊逻辑控制方法相比，新型多旋翼无人机噪声控制方法在移动群智感知机制的基础上，通过改变调度性能指标取值的方式，并根据板状结构振动特性，确定同步开关阻尼、短路开关阻尼、电感开关阻尼、外加电压源开关阻尼的计算表达式，又以蒙皮结构、加筋板结构、典型壁板结构为例，规划了噪声信号的实时布局形式。在实际应用方面，这种新型控制方法可以保证无人机噪声信号波动幅值在各个传输方向上始终处于相对较低的数值状态，对于维持多旋翼无人机的稳定运动能力起到较强的促进性作用。