超导薄膜磁-热不稳定与强非线性电磁本构的关联性*

王垚 姜璐 周又和 薛存

1) (西北工业大学力学与土木建筑学院工程力学系,西安 710072)

2) (西北工业大学航空学院,西安 710072)

3) (兰州大学力学与工程科学系,西部灾害与环境力学教育部重点实验室,兰州 730000)

常规导体的电磁本构关系一般满足线性欧姆定律,然而超导体的电磁本构关系呈现很强的非线性特征,所以与常规导体相比,超导有截然不同的电磁特性.本文基于超导材料E-J 幂次律本构关系,采用快速傅里叶变换方法(FFT),定量研究了不同环境温度、磁场加载速率以及临界电流密度条件下的超导薄膜磁-热不稳定性与非线性本构的关联性,揭示了强非线性电磁本构是导致超导薄膜磁-热不稳定性(呈现树状、指状磁通崩塌形貌)的重要因素,同时阐明了常规导体观测不到类似的磁-热不稳定现象的原因.另外发现由于超导薄膜抗磁性的增强导致超导薄膜边界磁场迅速增大,较大的磁压极易诱发磁通崩塌,所以超导薄膜内磁通崩塌阈值随幂指数的增加而降低.最后给出了 n0-jc0 和 n0-µ0 平面内不同非线性程度下超导薄膜内磁热不稳定状态的分界线.

1 引言

随着超导薄膜制备技术的成熟,由超导薄膜制备的超导滤波器、超导量子计算机、超导量子干涉仪等器件显示出更加优越的性能[1—3].然而,在超导薄膜元件使用过程中,研究人员观测到了磁热不稳定现象,这在常规导体中未曾出现过.无论是常规材料还是超导材料,均满足麦克斯韦方程组,两类材料的不同之处在于常规导体的电流-电压关系满足线性欧姆定律,而超导薄膜的电流-电压关系比较复杂,具有高度非线性的特性,其中磁通蠕动指数n决定了超导材料电磁本构非线性的程度[4].所以,超导薄膜高度非线性的电流-电压关系可能与磁热不稳定性相关,该特性降低了超导材料内磁通运动的稳定性.极大地限制了超导材料的实际应用[5].因此,超导薄膜的非线性特性及其内部磁热不稳定性[6,7]引起了科研工作者的广泛关注.

要得到超导材料的电流和磁场分布及其随时间的演化规律,不仅需要 M axwell 方程组,还要有反映具体材料性质的E-J关系.E-J关系称为超导材料的电磁本构,其中的参数由具体材料和服役环境决定.一般超导材料的E-J电磁本构具有复杂的强非线性特性.Bean[8]假设超导薄膜临界电流为常数,建立了著名的Bean 临界态模型.Kim等[9]基于Bean 模型,考虑了临界电流的磁场依赖性,给出了Kim 临界态模型.许多学者利用该模型解析求解了超导圆柱、超导圆盘和超导薄带内的磁场和电流分布,以及交流损耗问题[10—12].此外,许多研究人员对不同材料的电流-电压关系进行了大量实验测量[13—17],研究表明,当温度超过0 K时,超导内部磁通涡旋就会受到热激活作用,有一定概率脱离钉扎势束缚,由于空间变化的磁场导致磁通涡旋运动不对称,从而整体上看磁通涡旋朝一个方向蠕动(flux creep).所以,超导非线性E-J关系与磁通蠕动有关.为描述超导体中的磁通蠕动,Anderson[18]和Kim等[19]提出了Anderson-Kim 模型,该模型能很好地解释低温、低场状态下的磁通弛豫数据.Zeldov等[20]通过实验得出钉扎势U和电流密度存在着对数关系(U=U0ln(Jc/J)),进而提出了幂次律模型 (E=ρ0(J/Jc)n-1J/d).其中,n是与钉扎势有关的磁通蠕动指数,决定了E-J本构的非线性程度.随后,许多科学家测量了 B i2Sr2CaCu2O8+δ[21],YBa2Cu3O7[22,23],N b 和 V 等超导材料的V-I曲线,结果表明,采用幂次律模型能够很好地与实验数据符合.因此,幂次律模型被广泛用于磁通蠕动[24,25]、磁通渗透[26—30]、交流损耗[31—35]以及超导磁热稳定性[36—39]的理论和数值研究中.

磁热不稳定现象在第二类超导体中已经被实验观察到[40],这一现象引起了人们开展相关实验和理论研究的极大兴趣.磁热不稳定理论认为,第二类超导体处于临界状态时,其中的磁通涡旋会同时受到洛伦兹力和钉扎力作用而保持平衡.然而,当外磁场增大时,洛伦兹力会驱动磁通涡旋脱离钉扎而运动,这种磁通运动会产生大量焦耳热,如果不能及时耗散,将会造成超导材料局部温度的升高,而温度的升高又会削弱磁通钉扎力,诱发更多的磁通涡旋运动,正是这样的一个正反馈,导致磁热不稳定性的发生.常见的磁通跳跃和磁通崩塌都是磁热不稳定性的表现形式,其中,磁通跳跃现象常发生在超导块材和线材中,因为在块状或线材超导体中产生的焦耳热只能通过温度梯度缓慢地传播到边界处释放,这使得超导材料的温度需要更长的时间才能恢复到工作温度.利用实验手段,科研工作者研究了磁通蠕动、正常状态电阻率、工作温度T0、磁场变化速率、样品与外界环境的换热条件以及温度突变对磁通跳跃的影响[41,42].一些学者采用数值模拟方法,研究了平板和块体中磁通跳跃对各种电磁和热参数的敏感性[43—47].Wang等[48]提出了一种能够数值模拟超导线圈中磁通跳跃的方案,定性地研究了 N b3Sn 线材中磁热不稳定的主要特征.超导薄膜中的磁热不稳定常以指状或针状的磁通崩塌形式出现,因为超导薄膜与基底之间存在良好的热交换,使得薄膜中由于涡旋运动产生的焦耳热能够快速释放,减小了局部温度向四周扩散的可能.过去的几十年中,研究人员利用磁光成像技术(MOI)和其他实验手段,在 M gB2[49,50],Nb[51—53],YBCO[54,55],Y Ni2B2C[56]等多种超导材料内观测到磁热不稳定现象.Wang等[57,58]采用实验手段研究了激光对超导薄膜磁通崩塌演化过程的影响.为了进一步分析磁通崩塌的发生机制,研究人员采用理论和数值计算方法对磁通崩塌的产生及扩展进行了大量研究[37,39,59—62].Aranson等[63,64]采用线性摄动分析方法和快速傅里叶变换法(FFT)分别对磁通崩塌的触发条件及演化过程进行了理论数值研究.随后,Vestgården等[36,37,59,60]对FFT 方法进行改进,使其可以计算有限尺寸的超导薄膜内磁通动力学行为,并研究了不同形状的超导薄膜内磁通崩塌从成核到扩展至形成树枝状结构的演化过程.结果表明,虽然在一定条件下可以预测磁通崩塌发生时的磁场阈值,但其发生位置具有随机性,难以预测.因此,一般认为引发涡旋成核的微小扰动来源于涨落效应.磁通崩塌发生期间,大量磁通穿透超导薄膜并迅速向其内部运动,通常伴随着局部温度、电场以及磁矩的跳跃.其发生规模及频率与环境温度、磁场加载速率以及热扩散系数等多种因素有关[65—67].此后,Vestgården等[36,37,59,60]采用幂次律模型数值研究了不同形状的超导薄膜内磁通崩塌的产生及演化过程.Jiang等[68]给出了缺陷诱发薄膜磁通崩塌的新机制.Zhou等[62,65—67,69]研究表明磁通崩塌相关阈值与超导材料及大小、环境温度、外加磁场及传输电流等有关.然而,磁-热不稳定与强非线性电磁本构的关联性还不太清楚.本文采用快速傅里叶变换方法研究了具有不同磁通蠕动指数的超导薄膜内的磁通运动和磁热不稳定性,探讨了超导薄膜的本构非线性特性及其对超导薄膜磁热不稳定性的影响规律.本文其他内容主要包括3 个部分: 首先介绍用于计算超导薄膜内磁通动力学行为及磁热不稳定性的数值模型及方法,其次讨论不同参数情形下超导薄膜内的非线性特性对磁通运动和磁热不稳定性的影响规律,最后进行总结.

2 理论模型和方法

如图1 所示,考虑一个宽度为w,厚度为d的正方形超导薄膜,并将该超导薄膜置于温度始终保持为T0的基底上.当外加磁场等于零时,超导薄膜从正常态冷却到T0,随后,外加磁场开始随时间逐渐增加.

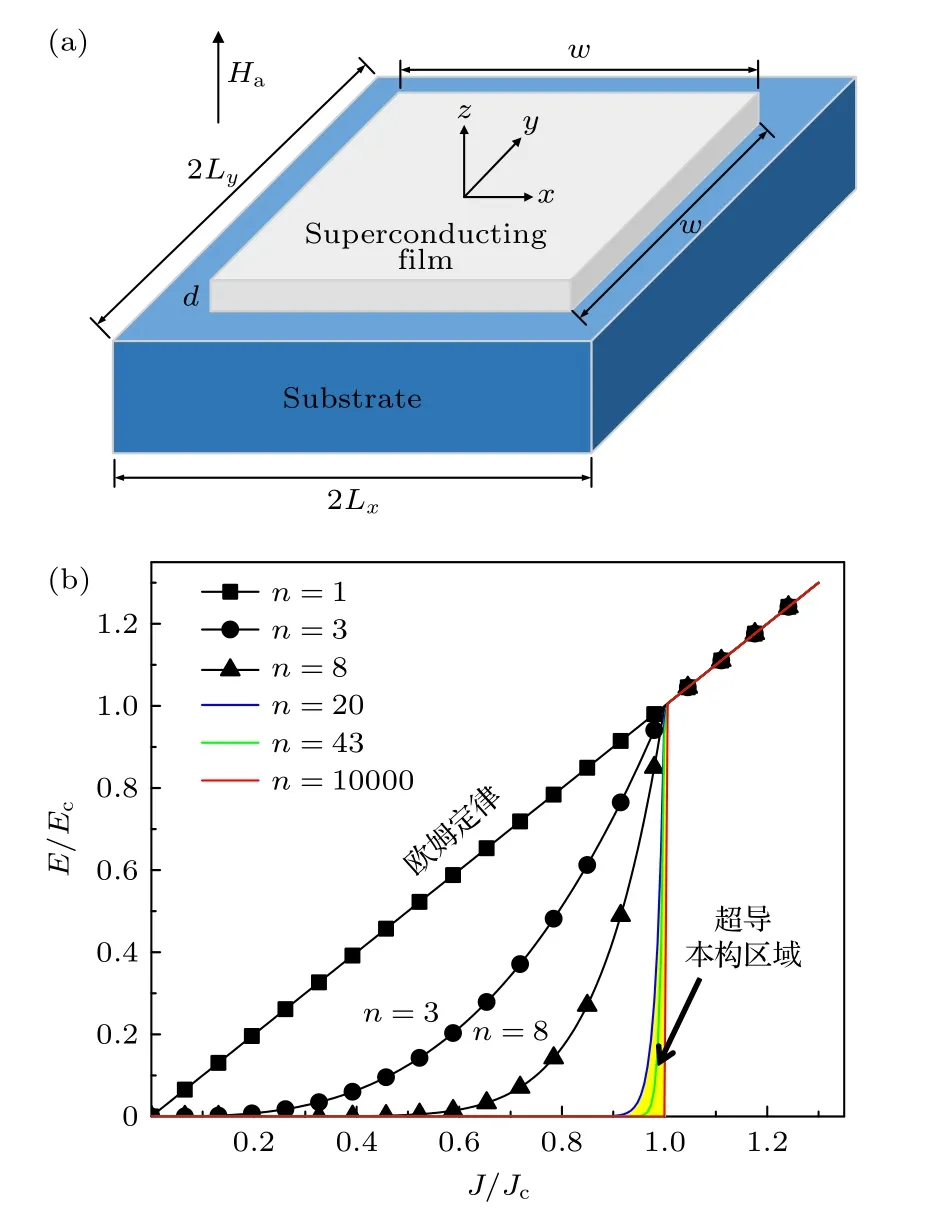
图1 (a)超导薄膜-基底系统示意图,外加磁场随着时间线性增加并始终垂直于超导薄膜表面,其中超导薄膜大小为w×w,数值模拟区域大小为2Lx×2Ly;(b)超导材料E-J幂次本构关系,n为磁通蠕动指数,图中黄色填充区域对应常见超导材料的 E -J 本构范围,常规导体对应n=1,即欧姆定律Fig.1.(a) Schematic diagram of the superconducting filmsubstrate system,where the applied magnetic field increases linearly with time and is always perpendicular to the surface of the superconducting film,where the superconducting film size is w × w and the numerical simulation region size is 2Lx × 2Ly;(b) E-J power instanton relationship for superconducting material,n is the flux creep index.The yellow filled area in the figure corresponds to the E-J instantonal range of common superconducting materials.The conventional conductor corresponds to n=1,denoting the Ohm’s law.

为了研究超导薄膜在上述零场冷却情况下的磁热不稳定性,通过求解Maxwell 方程并联立E-J本构关系和热扩散方程,得到超导薄膜内的磁场和温度场分布.超导薄膜满足Maxwell 方程:

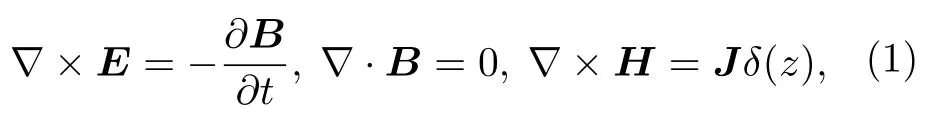
其中,B=µ0H,∇·J=0.假设超导薄膜厚度远远小于其边长,可以认为是无限薄情形,此时电流密度j的分布可以表示为j(x,y,z)=J(x,y)δ(z),其中J(x,y) 是面电流密度,δ(z)为德尔塔函数.为了计算超导薄膜内温度场随着时间的变化,数值求解如下形式的热扩散方程[36]:

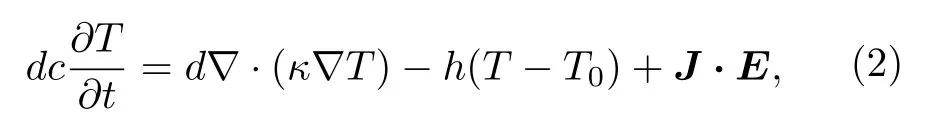
式中,J ·E为焦耳热,k和c分别为超导薄膜的热扩散系数和比热,h是超导薄膜与基底之间的导热系数,d是超导薄膜的厚度.Schneider等[70]实验发现低温环境下 M gB2的热传导系数与T3成正比.Denisov等[49]假设c=c0(T/Tc)3,h=h0(T/Tc)3,κ=κ0(T/Tc)3,计算了超导薄膜的磁通崩塌阈值,计算结果与实验相符合.Vestgården等[36]基于这个假设对 M gB2薄膜和Nb 膜的磁通崩塌问题展开了数值研究,获得了与磁光成像实验观测一致的磁通崩塌演化过程.因此本文采用此模型对超导薄膜内温度分布进行计算.对热扩散方程两边作傅里叶变换并整理,为提高求解稳定性,取T˙(t)→(T(n+1)-T(n))/Δtn,T(t)→(T(n+1)+T(n))/2[37],这里T(n)=F[T(tn)],Δtn=t(n+1)-t(n),得到傅里叶空间的温度场控制方程:

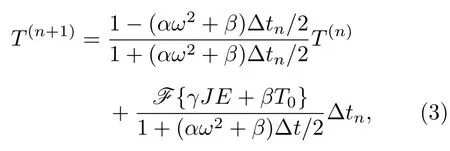
其中,α=κ/c,β=h/(dc),γ=1/(dc),计算完成后,对T(n+1)作傅里叶逆变换,即可求出温度场.超导薄膜高度非线性的E-J本构关系可表示为

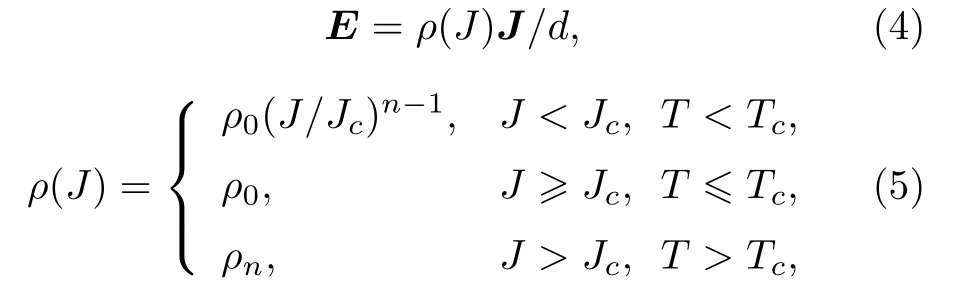
其中,ρ0表示薄膜内部所有被钉扎住的磁通受到洛伦兹力开始有磁通流动,但整体尚未失超时的电阻率;ρn为正常态时超导等效电阻率.一般情况下,在研究超导薄膜磁-热不稳定性时,常取ρ0和ρn相等[36].n表示磁通蠕动指数,反映超导材料本构非线性的强弱,与温度和磁场相关n=-U0(T)[1-B/Bc2(T)]/(kT),U0(T) 表示钉扎势.然而,本文研究的超导薄膜磁热稳定性主要与较小磁场(B ≪Bc2(T))下的涡旋热激活跳跃有关,且该过程伴有剧烈的温度升高,对于这里的n来说,温度变化占据主导地位.因此,这里忽略了磁场依赖性,采用n=n0(Tc/T),其中,n0是一个与温度无关的参数.而且该模型可以捕捉非线性涡旋动力学的主要特征,并与大量实验结果相符合[36,37].从数学方程角度,当n较大时,超导体表现为强非线性;当n较小时,表现为弱非线性;当n=1,则退化到常规导体的线性本构关系,即欧姆定律.如图1(b)所示,常见超导材料的E-J本构关系都在黄色背景区域内,其特征为电流密度J接近Jc时,电压发生突变,且随着n的增大,E-J本构的非线性逐渐增强,当n=∞时,该E-J幂次模型退化为Bean临界态模型.Tc表示超导薄膜的临界温度,Jc表示临界电流密度,它们之间关系为[36]

在超导薄膜的磁热稳定性研究中,Jiang等[68]通过采用磁场相关的Jc(T,B) 模型数值研究了超导薄膜边界裂纹选择性诱发磁通崩塌的行为,并成功揭示了实验观测到的缺口选择性诱发磁通崩塌的机理.Wen等[71]分别采用磁场相关的Jc(T,B) 模型和磁场无关的Jc(T) 模型与实验数据做对照.结果表明,采用磁场相关的Jc(T,B) 模型与实验数据符合良好.由于本文考虑均匀的超导薄膜,且重点关注E-J非线性程度与磁热稳定性的关联,所以没有改变更多的参数.实际上磁场影响了临界电流密度大小,本文也研究了不同的临界电流密度对磁热稳定性的影响.

为方便问题求解,引入局部磁化函数g=g(x,y)来表示面电流密度,两者之间满足J=∇×zˆg,zˆ表示垂直于薄膜表面的单位向量.根据安培定律,超导薄膜内的电流密度满足

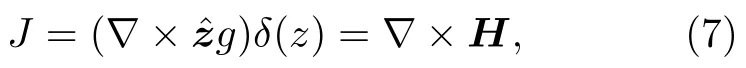
根据毕奥-萨伐尔定律,磁场分量Bz(r) 满足

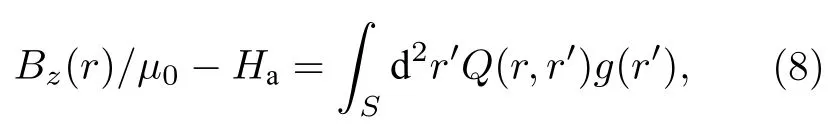
其中,Q(r,r′) 表示格林函数;Ha表示外加磁场;Hz表示超导薄膜内部总磁场,其傅里叶变换为F(Q)=k/2,k=|k|,该式可进一步处理为

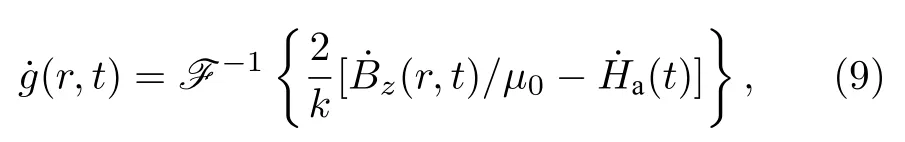
其中,F-1表示傅里叶逆变换.因此,超导薄膜内磁场演化模拟可由局部磁化函数得到

将该过程迭代求解s步后,薄膜外g˙(r,t) 变得很小(接近于零),此时 认为(r,t) 就是真实的g˙(r,t).根据g(r,t+Δt)≈g(r,t)+Δtg˙(r,t) 可求得下一时刻的磁化g(r,t+Δt).将上述过程不断迭代,得到关于局部磁化函数的演化过程.具体过程见参考文献[36].数值模拟区(2Lx×2Ly)离散为256×256的网格.这里,Lx=Ly=1.3×a,其中a=1.0 mm,为超导薄膜宽度的一半;d=100 nm 表示超导薄膜的厚度.超导薄膜的材料参数为Tc=9.2 K,jc0=Jc0/d=1.2×1011A/m2,ρ0=ρn=5×10-9Ω·m[38].对于热扩散相关系数,这里选择κ0=20 W/K·m,h0=104W/K·m2,c0=3×104W/K·m3[38].

3 结果分析与讨论

由于超导材料E-J本构关系表现为高度非线性,其中与钉扎势有关的磁通蠕动指数n决定了超导非线性的程度[4].因此,首先探究了磁通蠕动指数n对垂直外加磁场下超导薄膜的磁通运动和磁热不稳定性的影响.图2 给出了参数n0分别为3,15,26 情形下的超导薄膜在基底温度为2.5 K,磁场加载速率为5 T/s 的环境中的磁通穿透及磁热不稳定性.初始时刻,薄膜处于迈斯纳态,随着外加磁场的逐步增加,薄膜边缘处的磁场逐步增大,当外加磁场较小时(µ0Ha=1.8 mT),磁通从超导薄膜边界平滑(smooth)地向薄膜内部运动,并且磁通穿透速度随着磁通蠕动指数的增大而显著减小.这是由于较小的磁通蠕动指数意味着较低的钉扎势,磁通更容易脱离钉扎向薄膜内部运动,超导体抗磁能力越弱.当n=1 时,(4)式即为描述常规导体的欧姆定律.在垂直外加磁场下,磁通会迅速穿透常规导体薄膜,并均匀地分布.当外加磁场增加至一定值时,由图2 可知,n0较小时,磁场平滑渗透(smooth penetration)进入超导薄膜,直至接近完全穿透,系统始终处于磁热稳定状态.随着n0增加到一定范围,超导薄膜内出现磁热不稳定行为,磁通在超导薄膜边界成核,并迅速扩展进入薄膜内部,形成树枝状图案.此外,对比图2(b),(d)和(f) 可以发现,随着n0的增大,磁通崩塌规模不断减小,且发生频率随之增加.这是由于n0越大,超导薄膜抗磁性越强,外部磁压得不到释放,很快达到临界值,而且微小扰动对局部电场的影响越大,越容易发生磁通崩塌.在发生磁通崩塌时,n0越小,短时间内磁扩散速度越大,磁扩散区域也就越大,表现为磁通崩塌规模越大.

图2 通过数值模拟得到不同参数 n0 下的超导薄膜分别在外加磁场为µ0Ha=1.8 mT ((a),(c),(e))和 µ0Ha=4.0 mT((b),(d),(f))时的磁场分布.背景温度 T0=2.5 K,磁场变化率为5 T/sFig.2.Flux distributions of superconducting thin films with different parameter n0 at the applied magnetic fields ofµ0Ha=1.8 mT ((a),(c),(e)) and µ0Ha=4.0 mT ((b),(d),(f)).The substrate temperature is T0=2.5 K and the ramp rate is µ0 H˙a=5 T/s.

为了进一步研究磁通蠕动指数对磁通崩塌阈值的影响,数值计算了不同参数n0下超导薄膜内磁通崩塌阈值.图3(a)为磁通崩塌阈值随参数n0的变化曲线,其中曲线下方区域对应超导薄膜内磁通平滑穿透阶段,曲线上方区域对应磁热不稳定阶段.在背景温度场为2.5 K,磁场加载速率为5 T/s的环境下,当磁通蠕动指数较小时(参数n0＜11),无论外加磁场有多大,超导薄膜内始终没有磁热不稳定现象发生.随着磁通蠕动指数增大,薄膜内开始有磁热不稳定行为发生,并且第一次出现磁通崩塌行为的磁场阈值会逐渐降低.这是由于当磁通蠕动指数较大时,超导薄膜抗磁性增强,在相同磁场环境下,该超导薄膜边界处磁压更强.此外较大的n0意味着超导薄膜E-J非线性较强,在较低磁场下,超导薄膜内温度、电场或电流等受到微小扰动时,电流-电压突变更明显,导致超导体内的磁通状态更加不稳定.因此,当磁通蠕动指数较大时,即使外加磁场较小,也会使得超导薄膜的磁通状态容易发生突变,诱发磁通崩塌.图3(b)和图3(c)所示为不同磁通蠕动指数下的最大温度曲线和磁化曲线,由于在磁通崩塌过程中,超导薄膜内部温度场的峰值出现在崩塌位置.因此,这里仅考虑超导薄膜内部的最大温度,磁通每发生一次崩塌就伴随着磁化曲线的一次跳跃和温度的急剧升高,磁通跳跃的频率与温度急剧升高的频率基本一致.在磁通蠕动指数较小的时候(参数n0=3),没有磁通崩塌行为发生,也就没有温度的突变,磁化曲线也较为平滑,所以磁通蠕动指数n必须足够大(参数n0＞11)才能够观测到磁热不稳定性.随着磁通蠕动指数增大,开始有磁通崩塌行为发生,而且磁通蠕动指数越大,磁通崩塌行为发生得越频繁,磁化曲线表现为高频次、小幅度跳动,发生磁通崩塌行为时的最大温度相对较小,触发第一次磁通崩塌行为时对应的磁场阈值更小.

图3 (a)磁通崩塌阈值随着参数 n0 的变化规律,曲线下方表示薄膜保持磁热稳定状态,曲线上方表示薄膜出现磁热不稳定;(b)不同 n0 下超导薄膜的最大温度随外加磁场的变化;(c)不同 n0 下的磁化曲线图.数值模拟的背景温度为T0=2.5 K,磁场变化率为5 T/sFig.3.(a) The threshold field for the onset of flux avalanches in superconducting films with different n0.The lower region indicates the film is in magneto-thermal stable state,while the upper region indicates the thermomagnetic instability.(b) Maximum temperature and (c) magnetic moment in superconducting films as a function of increasing applied field for three different n0.The substrate temperature is T0=2.5 K and the ramp rate is µ0 H˙a=5 T/s.

由于超导磁通蠕动指数n=n0(Tc/T) 是关于温度的函数,因此,薄膜的背景温度会影响超导本构关系的非线性程度,从而影响超导的磁热稳定性.图4 给出了不同背景温度下参数n0分别为3,18,29 时超导薄膜内部的磁通分布.结果表明,当背景温度较低时(T=1.5 K),即使n0较小(n0=3),超导薄膜内也发生磁通崩塌行为,但随着背景温度的升高,在较小的n0下,磁场从超导薄膜边缘始终平滑地向薄膜内部渗透,直至接近完全穿透超导薄膜.但n0增加到一定值时(如n0=18),在相同温度和外加磁场下,超导薄膜内部有磁通崩塌行为发生(见图4(e),(f),(i)),当n0相同时,可以发现在相同外加磁场下,超导薄膜内的磁通崩塌数量随着温度的升高而减少,磁通崩塌由针状逐渐变为树枝状结构,其规模随着温度逐渐增大,该现象与实验结果一致[72].

图4 数值模拟了不同温度场下(T0=1.5,2.5,3.0 K),参数 n0 为3,18,29 时的超导薄膜在相同磁场 µ0Ha=3.1 mT 下的磁场分布Fig.4.Distribution of magnetic field Bz in superconducting fillms at the same applied field µ0Ha=3.1 mT with n0=3,18,29 and T0=1.5,2.5,3.0 K.

超导体的临界电流密度是材料内部钉扎势强弱的表现,而内部钉扎势必然会影响超导薄膜内磁通蠕动.因此,为了进一步研究临界电流密度对薄膜内磁通崩塌的影响.计算了参数n0=20,零场临界电流密度jc0分别取 6×1010,1 2×1010和24×1010A/m2情形下超导薄膜在外加磁场为1.6和6.2 mT 下的磁通分布.由图5(a),(c),(e)可知,临界电流密度的大小决定了超导薄膜抵抗磁通穿透的能力,在相同外加磁场下,临界电流密度越大,超导薄膜内的磁通穿透深度越小,意味着超导薄膜的抗磁能力越强.此外,临界电流密度也会影响超导薄膜的磁热不稳定性.如图5(b),(d),(f)所示,相同磁场下,当临界电流密度较小时,磁场会平滑渗透进入超导薄膜,直至接近完全穿透,薄膜始终处于磁热稳定状态.随着临界电流密度增大到一定值,薄膜内出现磁通崩塌行为,且磁通崩塌的规模随着临界电流密度的增大而减小,崩塌频率随之升高.

图5 通过数值模拟得到了外加垂直磁场分别为µ0Ha=1.6,6.2 mT 时,不同临界电流密度下的超导薄膜内磁场分布Fig.5.Magnetic flux distribution in supercondeucting films with different critical current densities at µ0Ha=1.6,6.2 mT.

图6 给出了超导薄膜磁通崩塌阈值随临界电流密度的变化曲线.可以看出,超导薄膜磁通崩塌阈值随着临界电流密度的增大呈指数降低,当临界电流密度增大到一定程度后,超导薄膜阈值变化逐渐减小,这与线性摄动分析结果一致[73].

图6 超导薄膜内磁通崩塌阈值随临界电流密度 jc0 的变化.曲线上方表示超导薄膜内磁热不稳定区域,曲线下方表示超导薄膜内保持磁热稳定状态Fig.6.The threshold field µ0Ha for the onset of flux avalanches as a function of critical current density jc0 The lower region indicates the film is in magneto-thermal stable state,while the upper region indicates the thermomagnetic instability.

由前面的分析可知,磁通蠕动指数和临界电流密度都会影响薄膜磁通崩塌行为.因此,通过计算多个不同临界电流及n0的超导薄膜的磁通阈值,获得了n0-jc0平面内超导薄膜磁热稳定性范围图,图7 给出了n0与临界电流密度共同调控时超导薄膜保持磁热稳定状态的界限.青色区域表示超导薄膜保持磁热稳定状态,磁通始终平滑穿透超导薄膜,直至接近完全穿透超导薄膜.黄色区域表示超导薄膜在励磁过程中出现了磁热不稳定现象.结果表明,适当降低临界电流密度和减小磁通蠕动指数都能有效提高超导薄膜的磁热稳定性.在二者同时调控时,这两个因素间有一定的关联,在磁通蠕动指数较大时,减小临界电流密度有助于提高超导薄膜磁热稳定性.实质上,临界电流密度和磁通蠕动指数都反映着超导薄膜内钉扎势的大小.当超导薄膜内临界电流密度较大或磁通蠕动指数较大时,超导薄膜退磁效应较强,相同外加磁场下超导薄膜外部磁压较大,因此容易诱发磁通崩塌,对应磁通崩塌阈值较低.

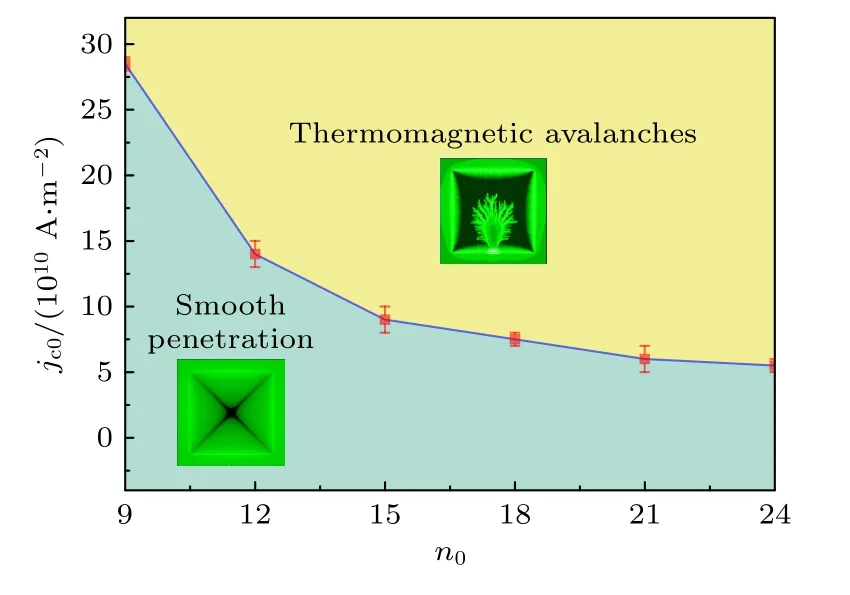
图7 n0 -jc0 平面内超导薄膜磁热稳定性/不稳定性的范围及分界线,图中黄色区域表示薄膜磁热不稳定,青色区域表示薄膜保持磁热稳定状态,误差棒表示分界线的精度Fig.7.Thermomagnetic stability/instability diagram in the n0-jc0planes.Yellow and green denote the regions of flux avalanches and smooth penetration.The error bars show the accuracy of the dividing lines.

图8 分别给出了外加磁场以2,9,15 T/s 的加载速率增加至1.8 mT (图8(a),(c),(e))和4.0 mT(图8(b),(d),(f))时,超导薄膜内的磁通分布.如图8(a)和图8(b)所示,在外磁场变化速率较低(2 T/s)时,超导薄膜具有良好的磁热稳定性,磁场能缓慢地渗透进入超导薄膜,不会出现磁通崩塌现象.随着外磁场变化率的增大,超导薄膜内部开始出现磁热不稳定,而且磁通崩塌的形貌由开始的树枝状崩塌转变为针状崩塌,崩塌频率显著升高,这是由于薄膜内磁通崩塌行为的发生是磁扩散和热扩散相互竞争的结果.在较大的磁场变化率下,磁扩散速度大于热扩散速度,外磁场以涡旋的形式渗透进入超导薄膜的过程中,由于涡旋运动造成运动路径上局部温度急剧升高,削弱了局部钉扎,使得外部磁场沿着前面涡旋运动路径迅速进入超导薄膜,来不及向周围扩散,宏观表现为磁通崩塌形貌分叉较少,呈针状崩塌.

图8 磁场变化率为µ0=2 T/s,µ0=9 T/s,µ0=15 T/s 情形下的薄膜内磁场分布 (a),(c),(e) 表示外加磁场加载到1.8 mT 时的薄膜内部磁场分布;(b),(d),(f)表示外加磁场加载到4.0 mT 时的薄膜内部磁场分布.背景温度场为T0=2.5 KFig.8.Magnetic field distribution in thin film at µ0Ha=1.8 mT ((a),(c),(e)) and 4.0 mT ((b),(d),(f)) for µ0=2,9 and 15 T/s.The substrate temperature is T0=2.5 K.

超导薄膜内部磁通崩塌行为的发生,与磁通蠕动指数和外磁场变化率都是相关的.因此,本文数值计算了多个不同n0及µ0下超导薄膜内的磁通运动,获得了n0-µ0平面内超导薄膜磁热稳定性区域范围(如图9),给出了不同n0及µ0下超导薄膜保持磁热稳定状态的界限.图中青色区域表示薄膜内始终保持磁热稳定状态,不会有磁通崩塌现象出现,黄色部分表示薄膜内发生了磁通崩塌行为.结果表明,减小磁通蠕动指数和降低外磁场变化速率都能有效提高超导薄膜磁热稳定性,在磁通蠕动指数较大的情况下,即使外磁场变化速率很小,也有可能诱发磁通崩塌行为,这是由于磁通蠕动指数越大,表示超导非线性越强,由(4)式和(5)式及线性摄动分析可知,当磁通蠕动指数较大时,即使受到很小的扰动,都有可能造成电流-电压关系突变,从而诱发磁通崩塌.

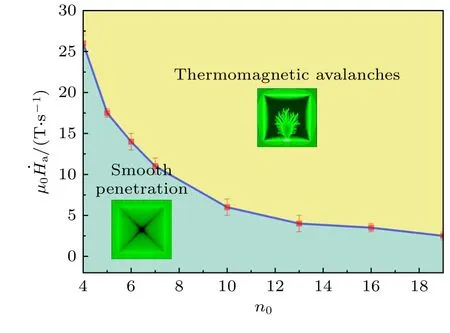
图9 n0-µ0 平面内超导薄膜磁热稳定性/不稳定性的范围及分界线,黄色区域表示薄膜内部磁热不稳定,青色区域表示薄膜保持磁热稳定状态,误差棒表示分界线的精度Fig.9.Thermomagnetic stability/instability diagram in the n0-µ0planes.Yellow and green denote the regions of flux avalanches and smooth penetration,respectively.The error bars show the accuracy of the dividing lines.

4 结论

本文采用FFT 理论研究了超导薄膜电场-电流的非线性特性,以及具有不同非线性强度的超导薄膜内磁热不稳定性.考虑了不同温度、磁场加载速率和临界电流密度下,磁通蠕动指数n对超导薄膜内磁通运动及磁热不稳定性的影响.与常规导体的线性欧姆定律不同,超导薄膜具有非线性E-J材料本构,且非线性程度随着磁通蠕动指数n的增加而增强.结果表明,当n0较大时,超导薄膜内磁通钉扎作用较强,超导薄膜抗磁性强,磁通较难穿透超导薄膜向其内部运动而导致边界磁场较大.因此,超导薄膜内的磁通崩塌阈值和崩塌规模随着n0的增大而降低,崩塌频率随之升高.此外,在不同n0下,超导薄膜阈值及形貌等均受温度、磁场加载速率以及临界电流密度的影响.通过计算多个不同环境及材料参数下超导薄膜内的磁通运动演化过程,分别给出了n0-jc0和n0-µ0平面内超导薄膜的磁热不稳定性范围,得到了不同E-J材料本构的非线性强度下超导薄膜磁热稳定/不稳定状态的分界线.