东印度洋海域风和降雨对环境噪声的影响*

柳云峰 李整林 秦继兴 吴双林 王梦圆 周江涛

1) (中国科学院声学研究所,声场声信息国家重点实验室,北京 100190)

2) (中国科学院大学物理学院,北京 100190)

3) (中山大学海洋工程与技术学院,珠海 519000)

4) (北京5111 信箱,北京 100094)

海面风和降雨对海洋环境噪声影响显著,利用海洋环境噪声模型结合风速和降雨率参数可对环境噪声谱级进行预报.本文研究了东印度洋海域环境噪声特性,分析了海面风速和降雨率对海洋环境噪声的影响规律,结果表明没有降雨时高频段噪声谱级与风速的相关系数可达0.59,存在降雨时高频段噪声谱级和降雨率的相关系数可达0.85,强降雨可使高频段环境噪声谱级增大6 dB 以上.同时修正了风生噪声源级公式使其适用于东印度洋深海环境,修正后模型预报强降雨噪声谱级与实验数据整体误差在2 dB 以内.利用小范围降雨噪声数据对模型进行验证时发现,在小范围降雨时噪声源模型采用海面非均匀降雨噪声源,比采用均匀噪声源的计算结果更加准确.修正后的风生及降雨噪声模型对东印度洋海洋环境噪声特性预报具有重要意义.

1 引言

海洋环境噪声作为水声信道中的一种干扰背景,长期存在于海洋波导中[1,2].各种类型的噪声源在不同频段和时间下起不同程度的作用,风生和降雨噪声是海洋信道中高频段噪声的主要成分.在声纳信号处理中,为了准确获知“信噪比”,噪声的强度、时空变化特征及统计特性等是声纳系统设计与使用必须考虑的参数.由于自然噪声源主导了海洋环境噪声级的基准分布,因此对于海洋环境噪声的研究也有助于海洋风和降雨的研究[3].

对于海洋环境噪声的大量研究指出,海洋环境噪声在不同海域和各种条件下的特性有所差异[4-10].Knudsen等[11]分析了二战期间大西洋及其他各海区的环境噪声,给出1 kHz 以上频段0—6 级海况下深海噪声谱.Wenz[12]在其深海噪声谱基础上,通过分析海上实验数据,总结出具有实用意义的Wenz 谱线,指出在0.5—5 kHz 的频带内随频率增大每倍频程降低5 dB.Knudsen等[11]和Wenz[12]通过实验数据总结出的海洋环境噪声经验谱线,展现了不同噪声源的主要作用频段和噪声谱级的基本分布情况.

关于噪声级和海面风速、降雨率的相关性,相关学者提出一系列经验回归公式来预报噪声级.在噪声级和风速的相关性方面,Piggott[13]分析了加拿大东岸浅海海域实验数据,给出风生噪声强度和风速对数线性相关的半经验公式.Vagle等[14]研究了海洋噪声和风速之间的关系,并给出了风速和8 kHz 噪声级的半经验公式,可以通过噪声测量定量给出风速的值.林建恒等[15,16]通过对青岛附近海域环境噪声及海面风速进行长期观测,研究了噪声级和风速对数之间的相关性.笪良龙等[17]基于连续3 个月潜标测量的南海环境噪声,指出0.8—5 kHz 范围内噪声级与风速相关性最好.Wang等[18]分析了风成噪声源的建模问题,并建立经验公式来描述风生噪声强度.在噪声级和降雨率的相关性方面,Nystuen等[19,20]发现降雨噪声强度大并且具有特殊的性质,可以用来监测和测量海面降雨.Ma等[3]分析了不同降雨量和风速下的环境噪声特性,并通过拟合实验数据得到噪声级与风速、频率等相关的经验回归公式,通过经验公式和海面风速与降雨等条件可以预报环境噪声级.国内在降雨噪声方面的研究主要集中在实验数据分析,以及降雨率与噪声强度之间关系的定性讨论方面.刘贞文等[21]指出了海洋降雨噪声有别于室内水滴实验辐射噪声具有复杂性,并宏观建立了降雨量与噪声功率谱的初步联系.魏永星等[22]利用长时间海洋环境噪声数据,分析了不同降雨率下噪声谱级的变化特征,指出降雨主要影响噪声频段为500 Hz 以上,暴雨时噪声谱近于“白噪声”比晴朗时高出约25 dB.徐东等[23]研究了台风过程中存在的降雨对海洋环境噪声的影响,指出在1—3 kHz 的频段内,台风中的降雨噪声要比风生噪声大5—6 dB,并根据半经验公式计算了降雨噪声谱.

由于不同海区的噪声源、海洋环境等复杂多变,噪声级和海面风速、降雨率的相关性也会有所不同,经验公式的适用性较差.随着研究的深入和实际应用需要,为了充分掌握风速、降雨率与相应环境噪声之间的关系,通常需要精确的海洋环境噪声预报模型.Carey等[24]使用抛物方程方法建立了噪声场模型,考虑了海面航船和风生噪声源,但未涉及降雨对噪声的影响.Harrison等[25]利用射线理论提出水平不变环境下的噪声场建模,并给出了计算噪声垂直指向性和噪声级的方法,但未给出降雨噪声的预报实例结果.何利等[26]分析了青岛附近海域长时间观测噪声数据,同时考虑海面均匀分布噪声源和附近离散分布船噪声的影响,提出适合于航道附近的海洋环境噪声模型.Jiang等[27]分析南海深海风占主导的环境噪声特性,通过射线模型给出不同风速下的噪声谱.汪洋等[28]基于射线理论构建了深海风生噪声计算模型,修正了噪声源公式,实现了南海实验海区不同风速下的噪声谱数值计算,但未包含有降雨噪声谱级的预报.

印度洋作为地球第三大洋,同时也是一个占据优越的地理位置和具有海权战略格局的大洋,但相比于其他的大洋,印度洋是最缺乏现场观测的热带大洋[29],我国对于印度洋海域的水声物理方面研究不足,对东印度洋海域的海洋环境噪声特性研究相对较少,发展适用于该海域的噪声预报模型至关重要.本文根据2019 年东印度洋深海实验获得的海洋环境噪声数据,对环境噪声级和风速、降雨率的相关性及降雨状况下环境噪声谱级的分布情况进行了分析,研究了风和降雨对海洋环境噪声的影响.基于射线理论,建立了海洋环境噪声预报模型,修正了风生噪声源级经验公式,使其适用于该实验海域,代入修正的风生噪声源级公式,该模型可准确预报强降雨噪声谱级.噪声模型使用海面非均匀分布降雨噪声源替代均匀分布噪声源,使其能够准确预报小范围降雨条件下的海洋环境噪声.

2 实验介绍

2019 年8 月,声场声信息国家重点实验室在东印度洋海域开展了深海声学综合实验,这是我国首次在印度洋开展声学实验,其主要内容之一是研究东印度洋海域环境噪声特性,实验期间对海洋环境噪声进行了记录.海上实验示意图如图1 所示,实验接收设备为深海声学潜标垂直接收阵(VLA).声学潜标主要由26 个自容式水声记录仪(USR)和温深传感器(TD)组成,USR 以非等间隔方式分布在水深70—3082 m 范围内,各个阵元上的USR采用同步工作模式,采集记录不同深度上的海洋环境噪声;TD 用来确定接收器USR 深度.USR 采样频率16 kHz,接收灵敏度为—170 dB,最低工作频率为20 Hz.在VLA 处测量的海水声速剖面(SSP)如图2 所示,海面处声速为1542 m/s,海底处声速为1508 m/s,可见实验海域是不完全声道.声速最小值为1493 m/s,对应深度为1692 m,但从约1100 m深度到约1800 m 深度声速变化缓慢,声道轴层“较厚”,与南海及西太平洋海域的声速剖面相比差异明显[30,31],并且在水深100 m 以浅存在表面声道.实验海区海底较为平坦,平均海深约为3095 m,后续分析中可以近似看作水平不变环境.实验海区的同步海面气象数据由国家海洋环境预报中心(NMEFC)提供,弥补了实验中观测的不足.NMEFC提供了空间分辨率1 km×1 km,时间分辨率1 min的模式同化风速和降雨率数据,覆盖环境噪声测量站位.

图1 噪声测量实验示意图Fig.1.The configuration of the noise measurement experiment.

图2 垂直阵处声速剖面Fig.2.Sound speed profile (SSP) at the VLA location.

3 风和降雨对环境噪声影响的数据分析

3.1 实验数据分析方法

选取声道轴附近深度阵元(约1589 m 深度)采集到的海洋环境噪声数据,计算1/3 倍频程的谱级 N Le(f0),计算表达式为

式中,Xi表示1 s 平稳时域噪声x(n) 在第i个频率下的快速傅里叶变换谱,f0是1/3 倍频程中心频率,fs是采样频率,N是平稳时域噪声数据的长度.nfH和nfL是以f0为中心频率的1/3 倍频程频段内的下界频率和上界频率,Mv是水听器的灵敏度.本文1/3 倍频程计算的起始中心频点是20 Hz,最高中心频点为6451 Hz.

3.2 环境噪声与风速和降雨率的相关性分析

海洋环境噪声是在稳定时间内变化缓慢的随机过程,随环境和噪声源具有明显的时间变化特性.图3 是实验期间噪声功率谱时间-频率二维分布,颜色表示噪声功率谱的值(单位dB,以1 µPa2/Hz为参考),同时给出同步的风速和降雨率.图3 中横坐标为时间,时间起止为2019 年8 月29 日9 时至2019 年8 月31 日15 时,左侧纵坐标为中心频率(单位Hz),频率范围为20—6500 Hz,右侧纵坐标为风速(单位m/s)或降雨率(单位mm/h).由图3可以看出,8 月30 日06:00—8 月30 日09:30 噪声谱级明显升高,8 月30 日15:00—8 月31 日02:00噪声也明显增强,噪声时频分布存在这两处谱峰.图4 给出了第1 个噪声谱峰值时接收潜标附近间隔1 h 的海面气象数据,图4(a)为对应时间的海面风速场,图4(b)为对应时间的海面降雨场.图5给出了第2 个噪声谱峰值时接收潜标附近间隔1 h 的海面气象数据,图5(a)为对应时间的海面风速场,图5(b)为对应时间的海面降雨场.图中红圈为实验站点位置示意,下面结合海面风速和降雨率情况对环境噪声的时间变化特性进行分析.

图3 噪声功率谱时间频率二维分布及同步风雨数据Fig.3.Noise power spectrum time-frequency two-dimensional distribution and synchronize weather data.

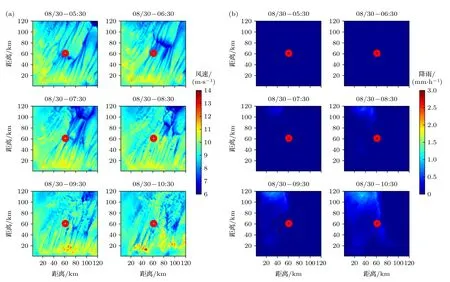
图4 8 月30 日05:30 至8 月30 日10:30 每1 h 海面气象 (a)海面风速变化过程;(b)海面降雨率变化过程Fig.4.Sea surface weather every 1 hour from August 30,05:30 to August 30,10:30: (a) Variation process of sea surface wind speed;(b) variation process of sea surface rainfall rate.

从图4 可以看出在第1 个噪声强度剧烈变化时段内(8 月30 日05:30—10:30),接收潜标附近的海面形成了一个高风速场.而结合图3 和图5 可以看出,在第2 个噪声强度剧烈变化时段内(8 月30 日19:30 至8 月31 日00:30),噪声强度明显变大,该时间段内没有明显的高速风场,但是存在一个强降雨过程.从上述分析可以基本说明,在存在强风或强降雨天气条件下,海洋环境噪声级会明显升高.

图5 8 月30 日19:30 至8 月31 日00:30 每1 h 海面气象 (a)海面风速变化过程;(b)海面降雨率变化过程Fig.5.Sea surface weather every 1 hour from August 30,19:30 to August 31,00:30: (a) Variation process of sea surface wind speed;(b) variation process of sea surface rainfall rate.

为了研究噪声谱级和风速、降雨率的相关性,首先在风生噪声主导的平稳时间段内(8 月29 日09: 00—8 月30 日08: 30,该时段内同步降雨率小于0.5 mm/h)分析不同频率下噪声谱级与风速的相关性,计算的相关系数结果如图6 所示.可以看出,在小于500 Hz 的频段,相关系数随频率升高整体增大,在500 Hz 相关系数达到0.59.在大于500 Hz 的频率范围,相关系数存在微弱起伏,但整体都大于0.5.一般而言,海洋环境噪声的中高频段风生噪声占主导,所以如图6 展示的结果,噪声谱级与海面风速具有较好相关性.

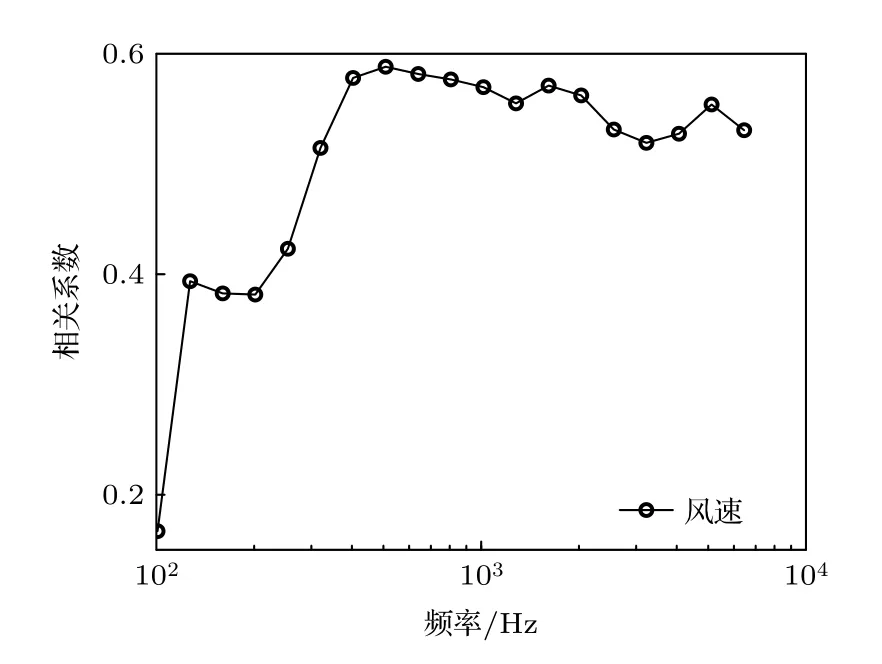
图6 噪声谱级与风速之间的相关系数(无降雨时)Fig.6.Correlation coefficient between noise spectral level and wind speed (absence of rainfall).

选取实验中风速处于实验期间谷值而降雨强度较大的时间段(8 月30 日18:50—至8 月31 日03:50),分别计算不同频率下的噪声谱级与风速、降雨率的相关系数,结果如图7 所示.可以看出,噪声谱级与降雨率的相关系数在500 Hz 以内随频率升高而增大,500 Hz 时达到了最大值0.85,高于500 Hz 时相关性略有起伏但维持在0.8 附近.同时可以看到,在该时间段内噪声谱级与风速的相关系数整体小于0.6,明显低于与降雨率的相关系数.上述分析表明,在该时间段内噪声谱级和降雨率的相关性明显强于其与风速的相关性,尤其在500 Hz 以上的频率范围内.

图7 噪声谱级与风速、降雨率之间的相关系数(有降雨时)Fig.7.Correlation coefficient between noise spectral level and wind speed and rainfall (in presence of rainfall).

3.3 降雨对环境噪声谱级分布的影响

海面风速和降雨率的变化,导致噪声谱级的概率密度分布也发生变化.选取实验中不同海面风速、降雨状况下的噪声数据,分析不同频率下噪声谱级概率密度的分布情况.分别选取未降雨时段(8 月29 日13:00—8 月30 日03:00)和降雨率大于2 mm/h 时段(8 月30 日17:40—8 月31 日00:20)的噪声数据计算不同频率下的噪声谱级概率密度分布,结果如图8 所示.图8(a)是在无降雨时间段内海洋环境噪声谱级的概率密度分布情况,图8(b)是存在降雨时段的结果.

在图8 中,红色点划线为噪声谱级的均值曲线,黑色点划线为噪声谱级的中值曲线,图8(a)中红色和黑色曲线基本重合.当未降雨时,海洋环境噪声谱级在1000 Hz 的中值为63.2 dB,均值为63.2 dB;在3500 Hz 的分布上限是56.8 dB,分布下限是52.8 dB.在存在降雨时,在1000 Hz 的中值为65.5 dB,均值为66.3 dB;在3500 Hz 频率谱级的分布上限是71.7 dB,分布下限是55.8 dB.通过分析可得,存在降雨时噪声谱级分布的上下限都比未降雨时高,并且存在降雨时噪声谱级的中值、均值以及谱级分布的最大概率对应值也均比无降雨时的高.查阅Wenz 曲线发现,当蒲福风级达到8 级时,海洋环境噪声谱级在1000 Hz 约为70 dB.实验过程中同步风速远小于蒲福风级8 级,但从实验数据计算出的噪声谱级概率密度分布可以看出,存在降雨时在1000 Hz 的噪声谱级上限远大于70 dB,由此说明强降雨过程对海洋环境噪声产生了重要影响.另外可以看到,实验期间存在降雨时噪声谱级分布的上限在3500 Hz 以上基本不随频率变化,这与文献[3]中的结论相符合.

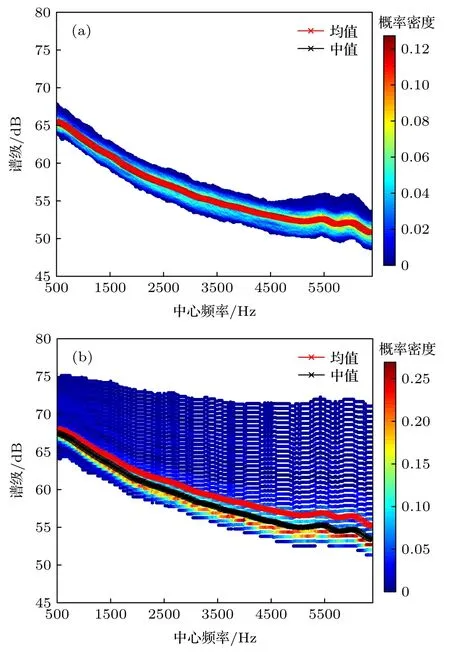
图8 未降雨(a)和降雨(b)时段噪声谱级的概率密度分布Fig.8.Probability density distribution of noise spectral levels for the periods of no rainfall (a) and rainfall (b).

选取实验中风速为9.8 m/s 时的无降雨时段数据和相同风速的强降雨时段数据(8 月30 日21:00 至21:50),分别计算两时段内的噪声谱级平均值比较,测量结果如图9 所示.可以看出,强降雨时段噪声谱级明显大于无降雨时段结果,且二者差异随频率升高而增大,在500 Hz 差异约为6 dB,在1000 Hz 约为8 dB,在6400 Hz 约为14 dB.上述结果证实了降雨对于高频段海洋环境噪声具有明显增强作用.

图9 无降雨和有降雨时段平均噪声谱级Fig.9.Average noise spectral levels during periods without and with rainfall.

4 噪声谱预报模型修正

4.1 噪声场射线模型

射线法对高频声场计算具有良好的适用性,计算速度快且物理意义清晰,能够适用于求解深海随距离变化环境中的声场.由于风生噪声和降雨噪声主要影响海洋环境噪声的高频段,因此本文采用射线方法建立环境噪声模型,结合相应的噪声源模型可以预报不同气象状况下的海洋环境噪声场.

三维噪声场建模采用柱坐标系如图10 所示,假设接收器位于图中z轴上,在水平海面内以接收阵为中心计算半径r范围内噪声源产生的噪声场.不同方位和距离的噪声源到达接收器的传播损失不同,对噪声场的贡献也不相同,需要将所有源贡献叠加得到噪声场.首先将计算海域按照角度分为L个方位分区,再按距离将计算半径划分成J个距离,则计算区域内的海面被划分为与方位角θl=lΔθ(l=1,2,···,L)和水平距离rj=r0+jΔr(j=1,2,···,J)有关的多个扇环,每个扇环的面积为Sj,l=rjΔθΔr.计算每个扇环内中心声源至接收点的声场,叠加后获得接收点的总噪声场.

图10 噪声计算模型示意图Fig.10.Schematic diagram of the noise calculation model.

假设互不相关的海面噪声源随机均匀分布在海面以下1/4 波长深度zs处的无限大平面上.单位面积的噪声源强度级为SL (dB),则单位面积的噪声源强度为ns2=10SL/10.用p(zr,j,l,zs) 表示位于水平距离rj、方位θl、深度zs处的声源在接收位置zr处产生的声压,用表示位于水平距离rj、方位θl的单位面积噪声源强度.为简化计算,根据互易原理将接收器位置作为计算声源点,将噪声源位置作为接收点,则接收点zr处的环境噪声场Pnoise(zr)可以由所有海面噪声源对接收点的贡献叠加获得[24]:

式中,*表示复共轭,〈〉号表示系综平均.将 (3) 式等号右侧〈〉内展开:

假设来自不同扇环面(即l ̸=l′或j ̸=j′)的噪声是互不相关的,则噪声互谱密度可近似为

关于噪声源强度ns2可以由噪声源强度级公式给出.

4.2 风生噪声源级公式修正

噪声源强度ns2可由噪声源强度级表示,包括降雨噪声、风生噪声、船舶噪声等噪声源强度级,使用文献中的噪声源强度级公式(下文以噪声源级公式代替).Harrison[25]给出的风生噪声源级公式:

式中,f为频率(单位Hz),U为风速(单位knots).降雨噪声源级公式SLR 采用Urick[34]给出的公式:

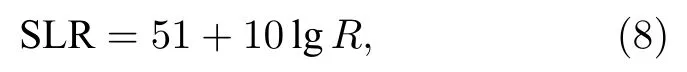
式中,R为降雨率(单位mm/h).船舶噪声源级SLS 使用Hamson[35]给出的经验公式:

其中,f为频率(单位Hz),vs为船舶航速(单位m/s),L为船舶长度(单位ft),N为每平方米面积内的船舶数量.噪声源强度ns2表示为

其中,SL为风生、降雨、船舶噪声源共同作用下的噪声源强度级.下文关注的500 Hz 以上频段主要是由风生噪声源和降雨噪声源影响,因此采用

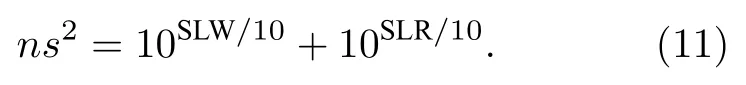
模型计算中使用实验测量的声速剖面,见图2.实验海区海底地形起伏较小,计算时忽略地形变化采用平坦海底地形.计算水平半径为60 km,水平方向角间隔为1°.海底使用双层液态海底,由一层沉积层和一层半无限基底组成,沉积层厚度为20 m,沉积层的密度为1.6 g/cm3,声速为1580 m/s,半无限基底的密度为1.8 g/cm3,声速为1700 m/s,沉积层和半无限基底吸收系数均通过公式给出[36]:

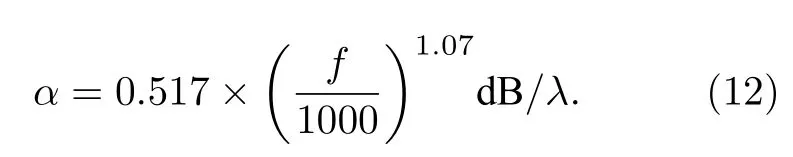
从同步海面气象数据可知,该海域在实验期间风速整体较高,风速变化区间较小,蒲福风级在5—6 级范围内.因此,计算风速9.8 m/s 和12.6 m/s(分别对应蒲福风级5 和6 级)条件下的噪声谱级.模型计算的噪声谱级和实验测量结果均值对比如图11 所示,图中实线为模型计算结果,点划线为实验测量结果.从图11 可以看出,模型计算结果和实验结果随频率变化的趋势存在较大差异,而且在500—3200 Hz 频段内仿真谱级和实验结果随风速变化的幅度趋势也存在一定程度的差异.由于模型输入参数中声速剖面和海底地形是实验测量结果,海底声学参数也经过传播实验结果验证相对可信,所以认为误差来源于模型计算中使用的噪声源级公式SL.

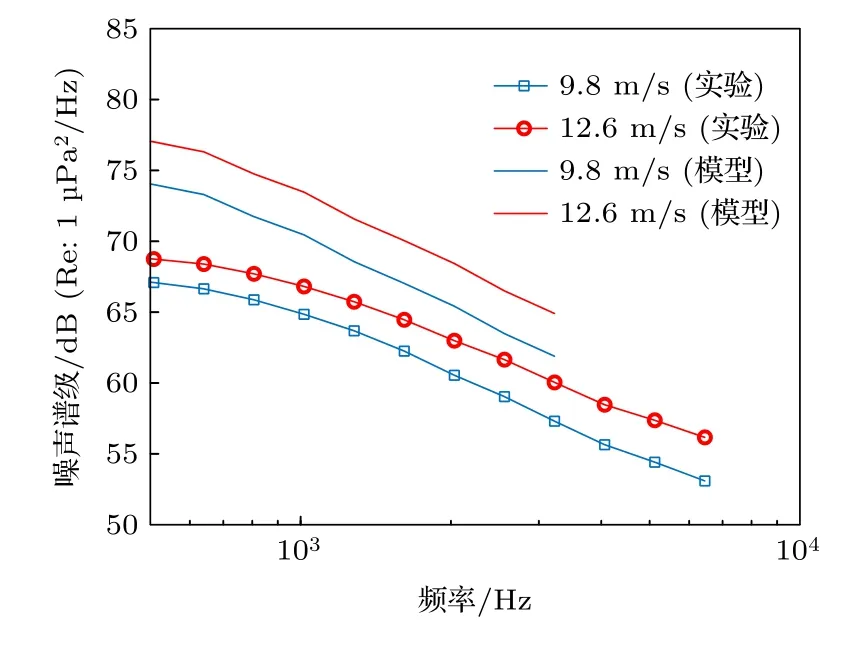
图11 不同风速下实验测量与模型计算噪声谱(修正前)Fig.11.Experimental measurement and model calculation noise spectrum at different wind speeds (before modified).

本文从风生噪声、降雨噪声联合的海洋环境噪声模型出发,通过与实验数据对比修正噪声源级公式参数,使模型更加适用于该实验海域.海洋环境噪声中,在不同频段下由不同种类的噪声源起主要作用: 在100—500 Hz 的低频段,主要噪声源是航船等声源[3];在500 Hz 以上的高频段,主要的噪声源是从波浪、湍流作用到降雨冲击海面再到风雨引起的气泡云振动等[37].因此,可对噪声源级公式分频段进行参数修正,本文主要关注风生噪声和降雨噪声为主的高频段噪声.在500 Hz 以上频段是由风生噪声和降雨噪声共同影响,在此频段内可利用未降雨时的噪声数据拟合风生噪声源级公式的常数项、频率相关项和风速相关项.待修正的风生噪声源级公式为

式中,S LWm为预修正风生噪声源级,其中C,a,b为需要修正的参数,频率f的单位为Hz,风速U的单位为m/s.此处需要强调,原有噪声源级公式没有覆盖3200 Hz 以上频段,为拓宽模型频率适用范围,在500—6400 Hz 频段内对风生噪声源级公式的参数进行拟合.采用最小均方误差法进行拟合,对参数C,a,b联合求解,最终获得的风生噪声源级公式为

图12 是修正后的风生噪声源级公式和Harrison 使用的风生噪声源级公式的计算结果比较,图中虚线是两种风速下Harrison 风生噪声源级,实线是两种风速下的修正风生噪声源级.可以看出,相同风速下修正后的风生噪声源级比Harrison[25]使用的风生噪声源级低,并且修正后的噪声源级随频率变化的斜率较修正前小.在相同风速下,修正后源级和修正前源级随着频率升高差距逐渐变小,在3200 Hz 附近二者差异约为5 dB.两个公式之间差异的原因,主要是环境噪声数据来自不同海区,Harrison[25]采用了地中海浅海噪声数据,而本文采用东印度洋海域深海噪声数据.将修正后的风生噪声源级公式代入环境噪声预报模型,采用与图11 相同的输入环境参数,计算相应风速条件下风生噪声级,并与实验测量结果进行对比,如图13 所示.可以看出,在风生噪声起主要作用的500 Hz 以上频段,两种风速条件下模型计算噪声谱级和实验测量结果吻合较好,误差在1 dB 以内,而且具有相同的随频率变化趋势.尤其对于3200 Hz 以上频段,总体误差也在1 dB以内,说明将原有噪声源级公式修正并扩展至更高频段是有效的.

图12 修正风生噪声源级(实线)和Harrison 使用风生噪声源级(虚线)Fig.12.Modified wind-generated noise source level (solid line) and Harrison’ s wind-generated noise source level(dashed line).

图13 不同风速下实验测量与模型计算噪声谱(修正后)Fig.13.Experimental measurements and model calculation noise spectrum at different wind speeds (after modified).

4.3 降雨噪声预报

本文修正后的噪声预报模型可以涵盖多种噪声源同时存在的情况,在降雨时无法将风生噪声和降雨噪声剥离开,模型可以预报两噪声源同时作用下的噪声场.下面针对3.2 节中提及的强降雨过程(8 月30 日21:00—21:50),进一步验证修正后的噪声预报模型.此时间段中存在明显降雨,降雨率达4 mm/h,海面风速5 级约9.8 m/s,计算该时段内噪声谱级均值如图14 中红色“ □ ”;为了对比有无降雨时环境噪声的差异,并验证模型预报的准确性,同时选取实验中没有降雨、海面风速约9.8 m/s时段内噪声谱级均值展示如图14 中蓝色“▷”.将未修正风生噪声源级公式代入噪声模型,预报相应降雨率和风速下的噪声谱级结果,此处假设接收点上方海面风和降雨对应的噪声源级均匀分布,模型预报存在降雨时噪声谱级为图14 中红色实线,未存在降雨的噪声谱级为图14 中蓝色实线.

从图14 可以看出,未修正的模型对于存在降雨过程的预报结果优于风生噪声预报结果,但是在1000 Hz 以下频段误差较大,这是因为在此频段内风和降雨对环境噪声都有较大贡献,风生噪声的误差影响了噪声预报总的结果.另外,由于Harrison[25]风生噪声源级公式未涵盖3200 Hz 以上部分,所以高频预报结果存在缺失.将修正后的风生噪声源级公式代入噪声模型,计算上述有无降雨条件下的环境噪声谱级,与实验结果的比较如图15 所示.

图14 有/无降雨时实测谱级(点线)与未修正模型预报谱级(实线)Fig.14.Measured spectral levels (dotted line) vs.unmodified model calculation spectral levels (solid line) with/without rainfall.

图15 有/无降雨时实测谱级(点线)与修正模型预报谱级(实线)Fig.15.Measured spectral levels (dotted line) vs.modified model calculation spectral levels (solid line) with/without rainfall.

从图15 可以看出,无论有无降雨过程,修正后的模型预报噪声谱级与实验数据在绝对幅值和趋势上都吻合较好,误差在2 dB 内,特别是在1000 Hz 以下频段预报精度明显提高.

上述模型预报降雨噪声时,假设降雨噪声源在海面均匀分布,这简化了模型计算的复杂度,对于海面气象参数精度的要求也相对较低.噪声源均匀分布即噪声源在不同方位和不同距离的分布情况和强度都相同,但由于不同方位和距离噪声源到达接收点的传播损失不同,对噪声场的贡献也不相同,叠加后即可得噪声场.但是,由于降雨在空间上有时是小范围的气象过程,而且降雨所影响的海面噪声源随时间变化较快,在降雨率较小或者降雨范围较小的气象条件下,假设降雨噪声源均匀分布可能会影响模型的预报准确性.而采用海面非均匀噪声源分布,由于海面降雨分布不同,噪声源在不同方位和距离的分布和强度也不尽相同,结合相应方位和距离的传播损失,将声场叠加即可得噪声源非均匀分布的噪声场.

选取实验过程中降雨率和降雨影响面积均较小时(8 月30 日23: 00 附近)的噪声和同步气象数据,分别使用噪声源均匀分布模型和噪声源非均匀分布模型对该时段噪声谱进行预报,并与实验测量结果进行比较,如图16 所示.可以看出,在该海面气象情况下,相比于降雨噪声源均匀分布的模型,噪声源非均匀分布的模型计算结果和实验测量结果吻合更好,误差在2 dB 以内,尤其在降雨噪声影响为主的2000 Hz 以上的高频段,噪声源非均匀分布的模型计算结果明显更优.这表明在小尺度或低强度降雨情况下,假设降雨噪声源在无限大海面均匀分布是不准确的,采用海面降雨噪声源非均匀分布的噪声模型计算更加真实可靠.

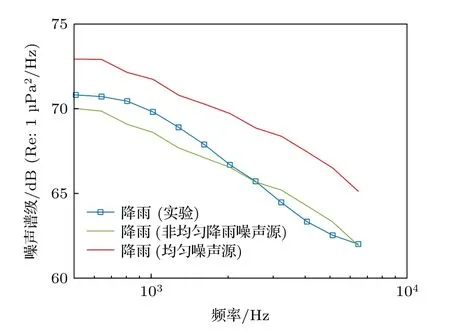
图16 局部降雨时模型预报降雨噪声谱(实线)和实验测量降雨噪声谱(点线)Fig.16.Model calculation of rain-generated noise spectral levels (solid line) and measured rain-generated noise spectral levels (dotted line) during local rainfall.

5 结论

利用2019 年东印度洋海域环境噪声观测数据,结合同步海面风速和降雨资料,研究了该海域海面风和降雨对海洋环境噪声的影响规律.在没有降雨的条件下,海面风对海洋环境噪声起主导作用,500 Hz 以下低频段内噪声谱级与风速相关性不强,500 Hz 以上高频段内噪声谱级随风速变化明显,相关系数可达0.59.在存在降雨时,噪声谱级和降雨率的相关性更明显,在500 Hz 以上频段相关系数可达0.85.实验数据中存在降雨时噪声谱级分布的上下限都比未降雨时高,并且存在降雨时噪声谱级的中值、均值以及谱级分布的最大概率对应值也都比无降雨时高.实验中9.8 m/s 风速下,在500 Hz 以上频段存在强降雨时噪声谱级比未降雨时高6 dB 以上.

基于射线理论建立了三维海洋环境噪声预报模型,修正了风生噪声源级公式,使其适用于东印度洋实验海域深海环境,能够准确计算各种风速和降雨率条件下的环境噪声谱级,模型计算结果与实验结果吻合较好,整体误差在2 dB 以内.在小范围降雨情况下,噪声预报模型采用海面非均匀分布降雨噪声源,得到的噪声谱级更为准确.修正后的风生及降雨噪声模型对东印度洋海洋环境噪声特性预报具有重要意义.

感谢参与2019 年夏季东印度洋声学实验的全体工作人员,是他们认真辛苦地工作为本文提供了可靠的实验数据.