超大直径盾构穿越黄河诱发地层沉降机理研究

李晓静刘成志杜昌言

(1.山东建筑大学 土木工程学院，山东 济南 250101；2.中铁十四局集团大盾构工程有限公司，江苏 南京 211899)

0 引言

随着我国城市圈的发展，越来越多的城市需要跨越黄河或长江以扩大自己的都市圈，增加发展空间。如南京修建五桥五隧以及多条地铁线北跨，大力发展江北新区；武汉市修建六桥五隧，将长江两岸紧密地联系在一起。目前，泥水平衡盾构施工法已成为穿江穿河隧道甚至海底隧道的主流施工方法，与土压盾构法相比，泥水平衡盾构法具有泥浆压力均匀、传递速度快、开挖面土压力平衡、控制精度高、刀盘扭矩小、刀具磨损小等显著的特点。泥水平衡盾构适用于含水量高的软土地基，尤其适用于跨河隧道、海底隧道以及在严格地面变形限制下大直径盾构隧道[1]。因此，许多软土地层中的大直径水下隧道采用泥水盾构法施工，如南京长江隧道[2]、杭州庆春路过江隧道[3]等。

盾构隧道开挖势必引起周围土体的松动和变形，直观表现为沉降或隆起。20世纪60年代，PECK[4]提出了可以预测隧道开挖沉降的公式(PECK公式)，并得到广泛应用。孙玉永等[5]应用现场监测和数值模拟相结合的方法，研究了盾构掘进施工引起周围地层位移场的分布规律。赵胤翔等[6]建立流固耦合模型，对盾构穿越富水粉细砂地层进行地表沉降模拟，发现了模拟曲线和实测曲线具有相同的趋势和规律性。谢雄耀等[7]对比了数值解和监测数据，验证了模型的合理性，进而研究泥水盾构过堤时大堤沉降的动态变化规律，并分析不同注浆压力对大堤沉降的影响。朱伟等[8]研究了开挖面支护应力不足引起开挖面的变形及破坏问题，探讨了隧道开挖面变形及破坏规律。白丁伟[9]通过采用线性回归分析法拟合分析实测数据，修正了沉降槽宽度和最大沉降量。代君等[10]通过数值模拟与沉降预测经验公式计算对比，得到盾构开挖过程的扰动影响范围。王剑晨等[11]搜集北京地区10个近接下穿工程的23组数据，拟合了既有隧道实测变形，发现93%的沉降数据符合PECK公式分布规律。陈春来等[12]通过分别计算先行盾构隧道和后行盾构隧道施工引起的土体沉降，叠加得到双线水平平行盾构施工引起的总的三维土体沉降。段绍伟等[13]修正了PECK公式，得到适用于长沙地区的PECK公式。唐晓武等[14]采用线性回归分析的方法，提出了软土地区随隧道埋深变化的地表沉降PECK修正公式。杨峰峰等[15]通过对不同直径的盾构隧道实施回归分析，修正出与实测数据曲线更加接近的PECK公式，为以后成都地区地铁修建、规划选线、沉降突变提供数据预测的支持。

文章根据盾构施工监测数据研究土体的沉降机理，使用有限元法模拟沉降过程，修正PECK公式使其适合计算黄河地层的沉降，研究结果可为黄河两岸城市实现跨黄河发展、修建黄河隧道工程，提供预测黄河中下游地区地层沉降的理论方法。

1 工程概况

被誉为“万里黄河第一隧”的济南黄河隧道工程首次采用了超大直径泥水平衡盾构穿越黄河，使用两台泥水平衡盾构机施工，其隧道全长为4.76 km，其中盾构段为2519 m。设计为双管双层盾构隧道，上层为市政公路双向6车道，采用现浇车道板方法施工；下部为城市轨道交通预留隧道，采用预制π形箱涵现场拼装法施工。刀盘直径为15.76 m、隧道直径为15.20 m，属于超大直径盾构隧道。由于没有以前的施工经验，存在很多不可预见性风险和技术难题[16]。黄河在中下游地区为地上悬河，盾构施工期间处于黄河汛期，河床压力大、稳定性要求高，故在盾构机下穿黄河时，控制土体扰动便显得尤为重要。盾构机在东线和西线分别穿越黄河后继续穿越民用建筑、城市高架桥梁、城市主干道等(如图1所示)。

图1 盾构隧道位置图

盾构机在下穿黄河过程最大覆土深度可达42.3 m，隧道最大水压为650 kPa，而最浅覆土为11.2 m(如图2所示)。盾构机穿越DK2+0监测断面时，切口压力设置为410～450 kPa，刀盘转速控制在1.1～1.5 r/min、掘进速度控制在15～25 mm/min，盾构机注浆压力为顶部注浆压力大于切口压力+50 kPa、底部注浆压力大于切口压力+250 kPa。穿越地层主要为粉质黏土层、砂层以及分布不均的钙质结核层，该地层岩土物理力学参数见表1。

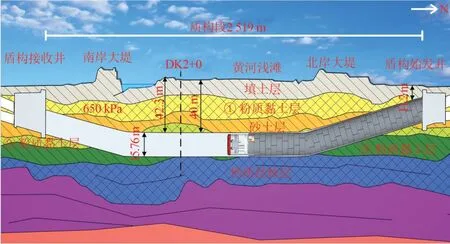
图2 盾构穿越黄河纵断面图

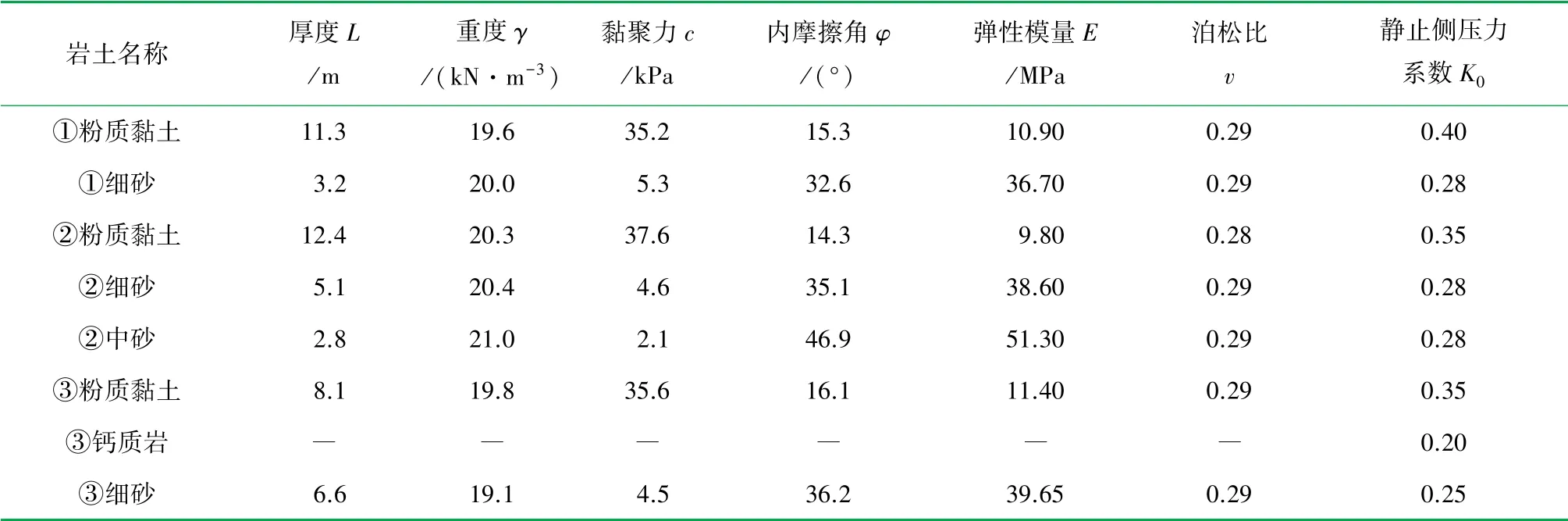
表1 岩土物理力学参数表

2 盾构下穿黄河地层沉降监测与分析

黄河浅滩位于南北大堤之间(如图2所示)，一旦黄河进入较为严重的洪水期，浅滩区便成为北岸大堤之前的最后一道壁垒，因此黄河浅滩地层稳定显得尤为重要。以黄河浅滩DK2+0断面为研究对象，以沉降监测数据来判断此位置地层的位移变化情况，沉降点布置如图3所示。

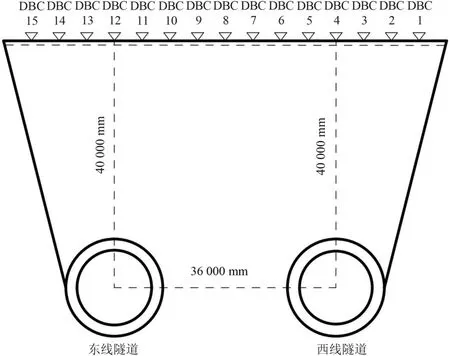
图3 DK2+0断面沉降点布置图

由图3可知此断面隧道埋深约为40 m。在东、西隧道断面地表布置了DBC-1—DBC-15共15个沉降监测点，每个监测点大约间隔4.5 m。其中，监测点DBC-12和DBC-4分别位于东线和西线隧道正上方，DBC-8位于两隧道中心线的中间，两隧道中心线间距为36 m。

DK2+0断面沉降监测曲线如图4所示。盾构机到达土体不同阶段，对土体变形的影响不同，根据DK2+0断面监测数据分析其沉降阶段。

图4(c)中Ⅰ阶段东线盾构机逐渐逼近DK2+0监测断面，此处土体受到盾构机切口压力自然挤压而挤密发生固结，孔隙水压力减少，有效应力增加，土体产生固结引起沉降。通过图4(a)和(c)可知，这一阶段沉降较小。由图4(e)和(f)中的Ⅰ阶段可知，虽然此位置沉降监测点距离开挖隧道中线较远，但在盾构机未到达阶段断面时也发生了细微的沉降变化。

图4(c)和(d)中的Ⅱ阶段分别为东线和西线盾构机即将到达DK2+0监测断面阶段。通过图4(a)和(b)可以发现，这一阶段个别监测位置发生了隆起现象，如西线断面的DBC-4、DBC-5，东线断面的DBC-12、DBC-13。这是由于此阶段盾构机对前方土体扰动开始增大，掌子面前方土体发生变形，孔隙水压力增加，总应力增大，土体压缩产生弹塑性变形。

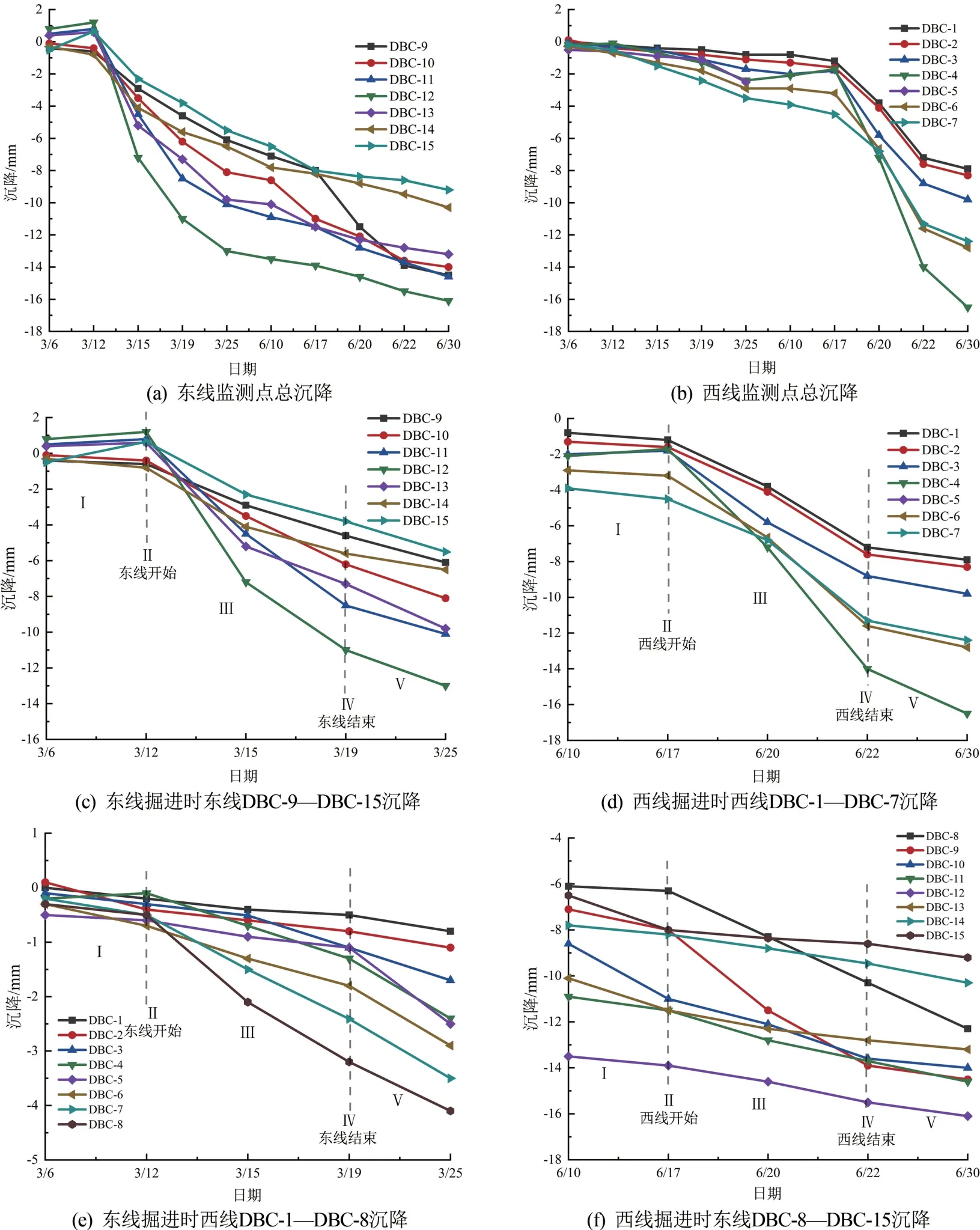
图4 DK2+0断面监测点沉降对比曲线图

图4(c)和(d)中Ⅲ阶段分别为东、西线盾构机通过DK2+0监测断面阶段。通过图4(c)和(d)可以看出，此阶段对土体的扰动是最大的，盾构掘进过程中盾壳与地层之间产生摩擦阻力作用，会产生一个滑动面，邻近滑动面的土层中产生剪切应力，当盾构机刚通过受剪切破坏的地层时，因受剪切而产生的拉应力导致土壤立刻向盾构后的空隙移动，土体应力释放，出现弹塑性变形，产生较大沉降。在支护过程中，盾构开挖与管片拼装过程之间存在一定的时间差，此时支护力小，沉降较大。当管片拼装结束后，衬砌开始承受周围土压力，此时沉降过程变缓。由于在开挖过程中土体应力被释放，土体仍会产生次固结沉降，此时仍需要注浆加固。

图4(c)和(d)中Ⅳ阶段分别为东、西线盾构机的盾体完全离开DK2+0监测断面阶段。在盾尾通过后，由于盾构尾部和衬砌之间存在物理间隙，土体逐渐失去了盾体的支撑，即便施工过程中进行同步注浆填充地层间隙，但是由于地层的不均匀性、注浆压力的控制困难、注浆量损失等多种因素，无法及时充填是必然的，注浆不及时的空隙会被周围土体填充，导致地面过度沉降。如图4(c)和(d)所示，注浆完成后依旧会产生一定的持续沉降，此时为盾构通过后沉降阶段。

图4(c)中Ⅴ阶段东线盾构机离开监测断面土体后，砂浆开始固结，体积缩小，导致土体持续变形，应力松弛，产生徐变，形成固结沉降。但是变形逐渐减小，微乎其微。

隧道正上方监测点沉降曲线如图5所示。东线隧道掘进期间，隧道中线正上方监测点DBC-12沉降最大，西线隧道掘进期间则是监测点DBC-4沉降最大，符合PECK预测模型中最大沉降的一般规律。2020年3月12日和6月17日东、西线盾构机刀盘即将到达监测断面位置，由于盾构刀盘切口压力增大，压缩土体，发生了轻微隆起现象。图5中Ⅱ阶段东线盾构机通过监测断面，此时DBC-12监测点发生了明显沉降，而距离东线隧道中线较远的DBC-4监测点则沉降变化值较小。因此，在盾构掘进过程中，隧道中轴线正上方土体沉降最为严重；随着监测点与隧道中轴线的距离增加，最大沉降Smax减小。

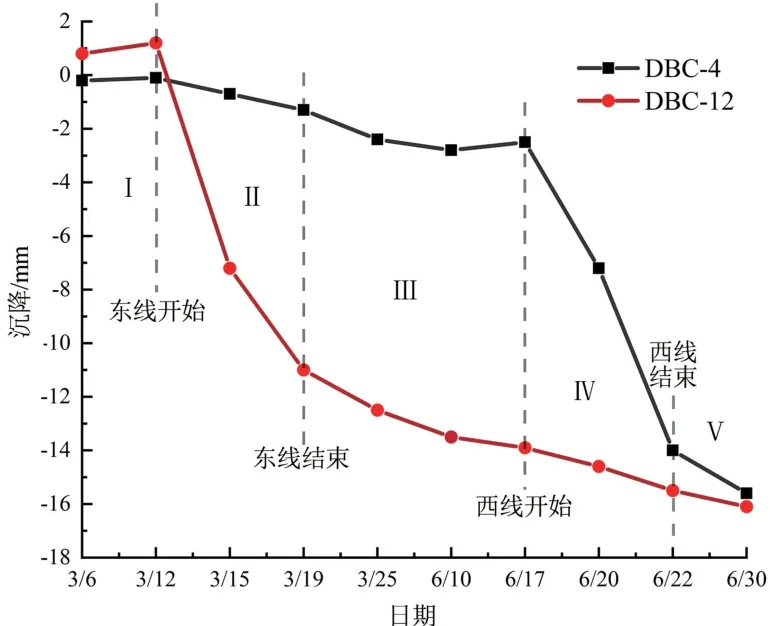
图5 隧道正上方监测点沉降曲线图

由以上各沉降时期可知，盾构推进引起的地表沉降按沉降变化规律可分为盾构到达前沉降、盾构到达断面沉降(或隆起)、盾构通过沉降、盾尾脱离沉降和长期持续沉降等5个阶段。通过对各阶段沉降数据分析，得出各掘进阶段对黄河地层的影响程度，如图6所示。

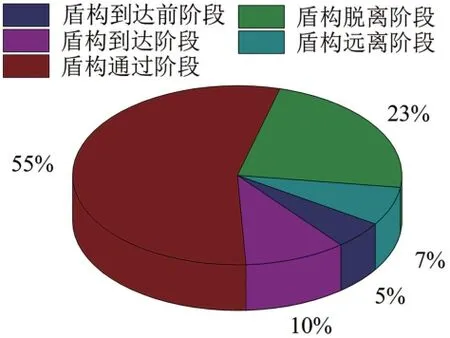
图6 盾构各阶段对土体扰动占比图

在盾构通过阶段对土体的扰动影响最大，同时对地层的稳定影响最严重，但是在施工过程中通过控制盾构机掘进姿态、切口压力、刀盘转速、掘进速度以及注浆压力等，地表沉降满足施工规范中规定值＜20 mm的要求。

3 盾构下穿黄河地层数值模拟

3.1 模型建立

结合济南黄河隧道工程，以东线隧道穿越黄河为例，使用ABAQUS有限元软件建立三维数值模型，尺寸为60 m×36 m×50 m(垂直于隧道轴线的宽度×沿隧道轴线长度×高度)，分3段开挖，每段长为6 m。其中，隧道开挖直径D为15.76 m、衬砌外径L为15.20 m。模型至隧道边缘的左、右边界分别取2D，盾构机壳体与衬砌外壁之间的环形物理间隙Gp为0.2 m。隧道沿轴线方向长度取36 m、衬砌厚度取0.65 m，其注浆厚度为0.30 m，隧道中轴线埋深H为40 m。模型在X、Y和Z方向的位移固定在隧道底部。法线约束应用于模型的正面和背面，以及模型的两侧，模型的顶面是自由位移边界，不受约束[17]。在掘进过程中利用删除单元模拟开挖过程。通过调整间隙单元的刚度来模拟盾构机的临时支撑，通过调整盾尾物理间隙的模量来模拟注浆。注浆压力分别以相同的量和相反的方向施加于衬砌的外边界和开挖边界。盾构切口压力对地层压力的平衡作用由隧道施工面处隧道轴线方向的均匀压力模拟[17-18]。

采用Drucker-Prager模型作为土体的本构模型。此模型在模拟盾构开挖粉质黏土时，能很好地反映主应力、剪应力以及体积应力对土体的影响[18]。此外，此模型还考虑了静水压力的影响，克服了Mohr-Coulomb模型在这方面的弱点，更加适用于黄河下游地区土体特征。

3.2 模拟结果及分析

土体位移和应力云图如图7、8所示。在开挖隧道中线正上方的土体沉降最大，随着土体远离隧道中线，沉降的逐渐减小，与监测数据分析结果一致。

盾构机开始推进时，如图7(c)所示，土体发生较大扰动，开挖土体上方开始发生较大沉降，一直延续至土体上部表面(即所模拟的DK2+0监测断面地表)。在盾构机通过后，盾体脱离土体，土体应力释放严重(如图8(a)所示)，产生弹塑性变形，引起较大沉降。由图8(b)可以看出，当盾构机推进至第二阶段，由于盾体对土体存在支持力，仅在开挖面附近的土体应力释放较为严重。

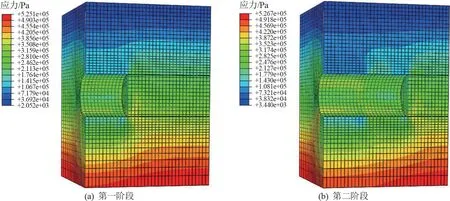
图8 土体开挖应力云图

随着管片拼装的完成，衬砌的支护力开始反作用于土体上，土体应力变化情况开始削弱，此时对上部土体的沉降影响开始减小(如图7(b)所示)，沉降云图开始向掌子面上方移动(如图7(d)所示)。直到注浆层开始硬化凝结完成，支护力开始反作用于土体时，土体的沉降才逐渐步入平稳变化，与施工数据反应的结果吻合。

由图7可以看出，隧道底部发生了隆起现象，隆起的主要原因是盾构机切口压力导致开挖面土体应力增大，土体压缩产生弹塑性变形导致。由于此工程位于黄河底部，孔隙水压力大，在完成衬砌支护以及注浆支护后，隧道下方土体会向上挤压衬砌，造成管片上浮现象[19](如图7(c)所示)。

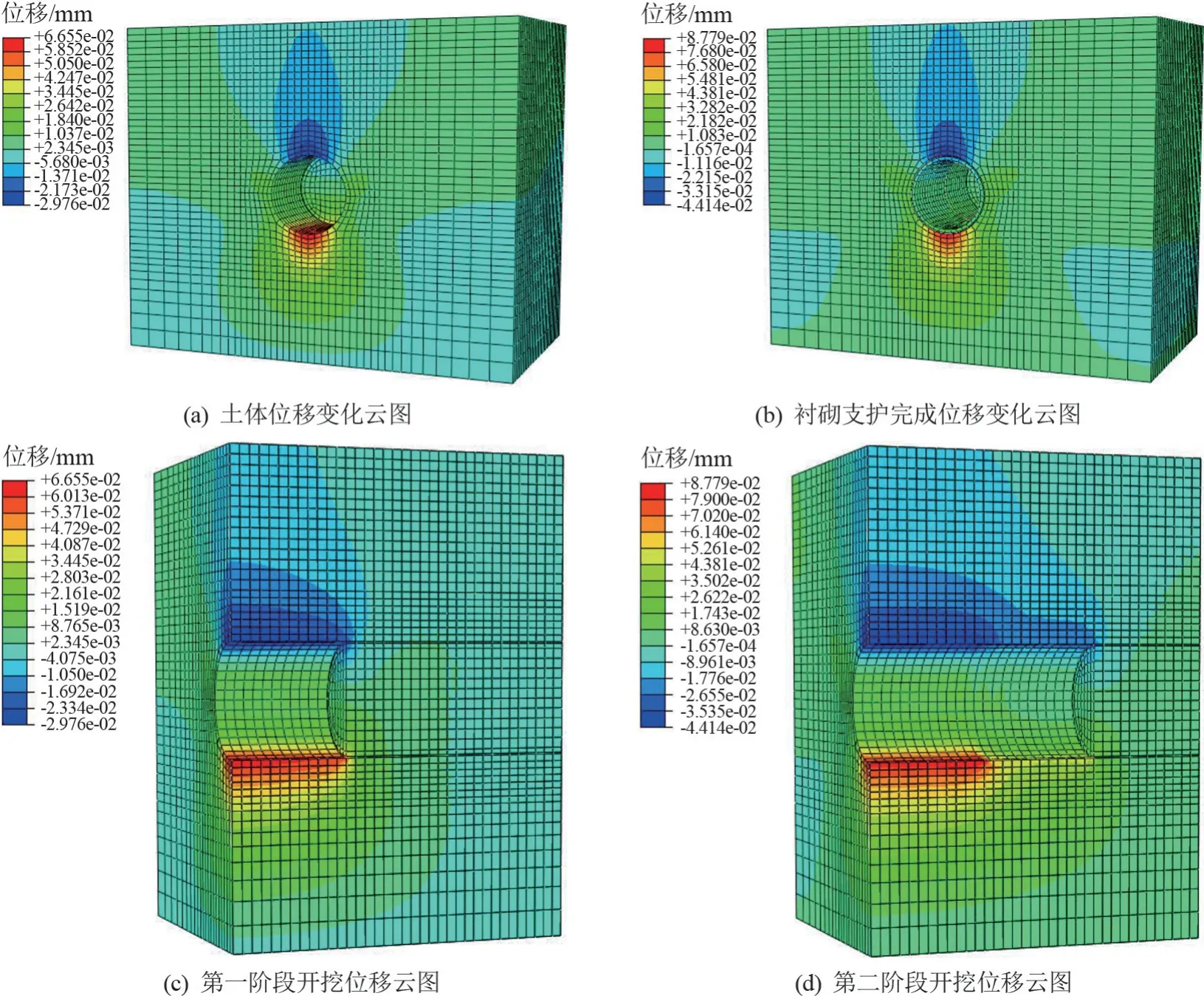
图7 土体位移云图

总体沉降发生过程以及土体应力变化过程符合3.1节盾构开挖5个沉降过程，表明盾构开挖土体沉降规律具有一般性，沉降槽宽度发展趋势与PECK公式预测模型基本吻合。

3.3 模拟结果验证

将东线隧道正上方DBC-12监测点的沉降数据与数值模拟结果做对比，如图9所示。模拟沉降为12.7 mm、监测沉降为14.3 mm，其差值＜7.8%。因此，模拟结果与监测结果变化趋势基本吻合，表明此数值模型可以很好地模拟黄河地层在大直径盾构掘进时的沉降情况。图9中0～2 m阶段的数值模拟值未发生变化，这是因为数值模拟在开始的时候未考虑初始沉降，造成沉降状态的差异性[7]。

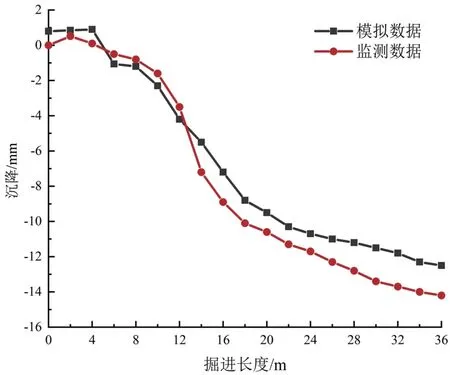
图9 沉降模拟结果与监测结果对比曲线图

4 基于监测数据的PECK公式沉降预测研究

4.1 经典PECK公式

近年来，随着盾构施工的发展，越来越多的地下空间工程采用盾构法施工，地层损失率以及地表沉降计算成为地下工程学者们关注的焦点问题[9-15]。PECK方法[4]成为地下工程中使用最多的经验方法。然而，受工程种类、地层、工法等限制，对结果有很大影响的两个重要参数沉降槽宽度i和最大沉降Smax很难确定[20]。粉质黏土地层中的参数i和Smax，可以通过回归分析监测数据估算[9]。

文章所依托工程是人类首次穿越地上悬河工程，并且隧道开挖直径大，主要穿越粉质黏土地层，对最大沉降和沉降槽宽度变化影响较大。故需要结合实际工程对PECK公式回归分析，判断是否适用于此类工程地表沉降预测。

地表沉降示意图如图10所示，其中W为地面沉降槽总宽度。横断面沉降与最大沉降计算公式由式(1)～(4)表示为

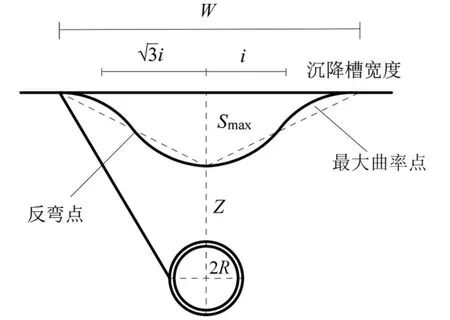
图10 地表沉降示意图

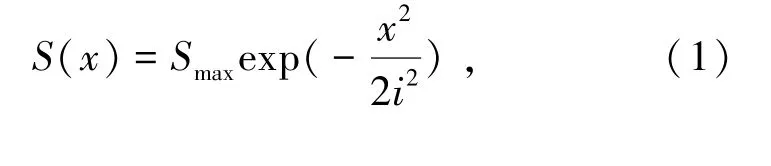
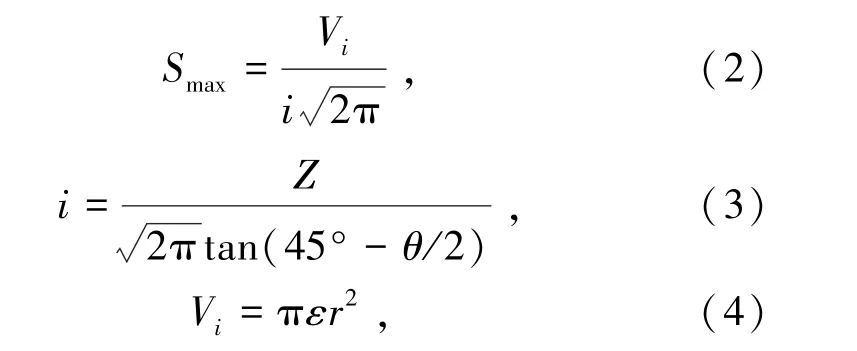
式中S(x)为x位置处由底层损失引起的地表沉降，mm；Smax为地表最大沉降，mm；x为测点与盾构掘进线路中线的距离，m；Z为地面到隧道中心点的距离，m；i为沉降槽宽度，m；Vi为开挖过程中单位长度损失地层体积，m3/m；θ为地层内摩擦角，°；ε为单位长度地层损失率；r为盾构机开挖半径，m。

4.2 东西线监测数据回归分析

经过线性回归分析，得到回归后的方程由式(5)表示为

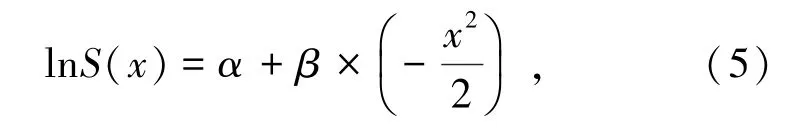
式中α为线性回归方程常数项；β为线性回归方程自变量系数。

由回归分析过程求得α和β，分别由式(6)和(7)表示为

取隧道DK2+0处东线和西线监测断面数据，结合式(1)和(3)，拟合沉降曲线，结果见表2、3。

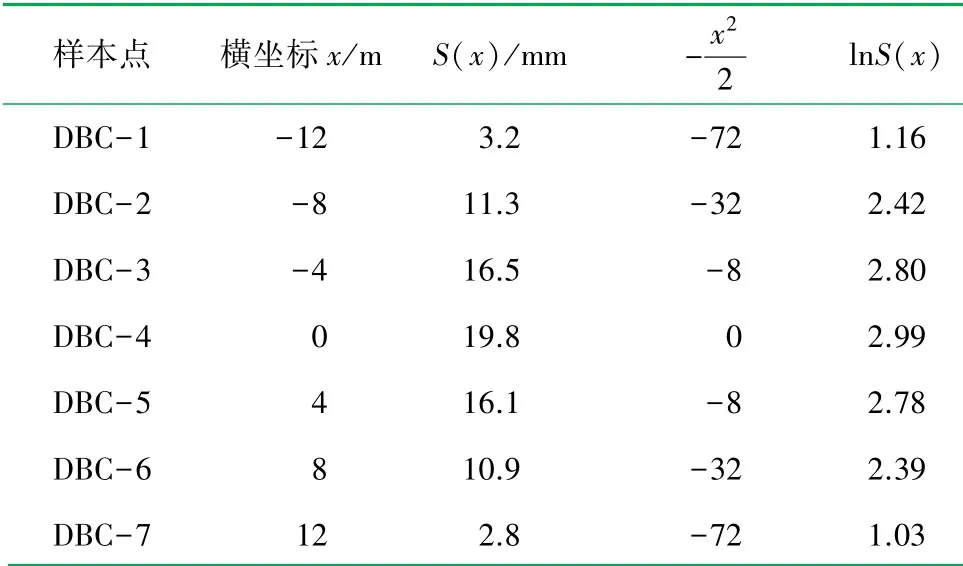
表2 西线断面监测数据回归分析表

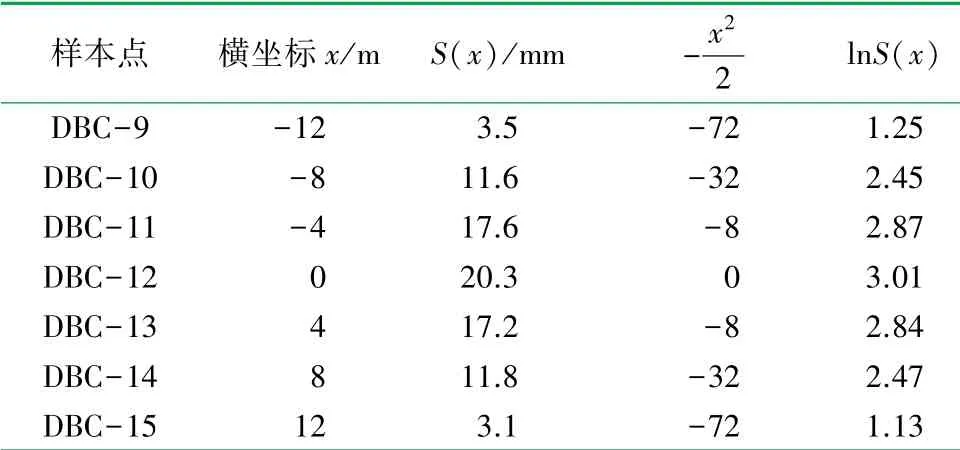
表3 东线断面监测数据回归分析表

根据DK2+0断面沉降监测数据和回归函数曲线绘制东西线断面数据回归情况，如图11所示。

西、东线断面线性回归函数分别为lnS(x)＝3.07+0.0264×(-x2/2)和lnS(x)＝3.11+0.0257×。采用线性相关系数R检验其线性相关关系，根据西、东线断面监测数据计算得到R2的值分别为0.974、0.970，R2越趋近于1，表明其相关性越大。

由R检验结果可知沉降回归曲线与实测数据线性相关性较好。并且通过图11拟合结果可知，东、西线断面拟合曲线与实测数据拟合较好，故证明拟合后的PECK公式可以用来预测盾构机穿越黄河中下游软土地层的沉降情况。通过式(1)～(3)求得PECK公式预测曲线如图12所示，PECK公式预测曲线与监测断面实测曲线误差较大，需要对其修正后方可使用。

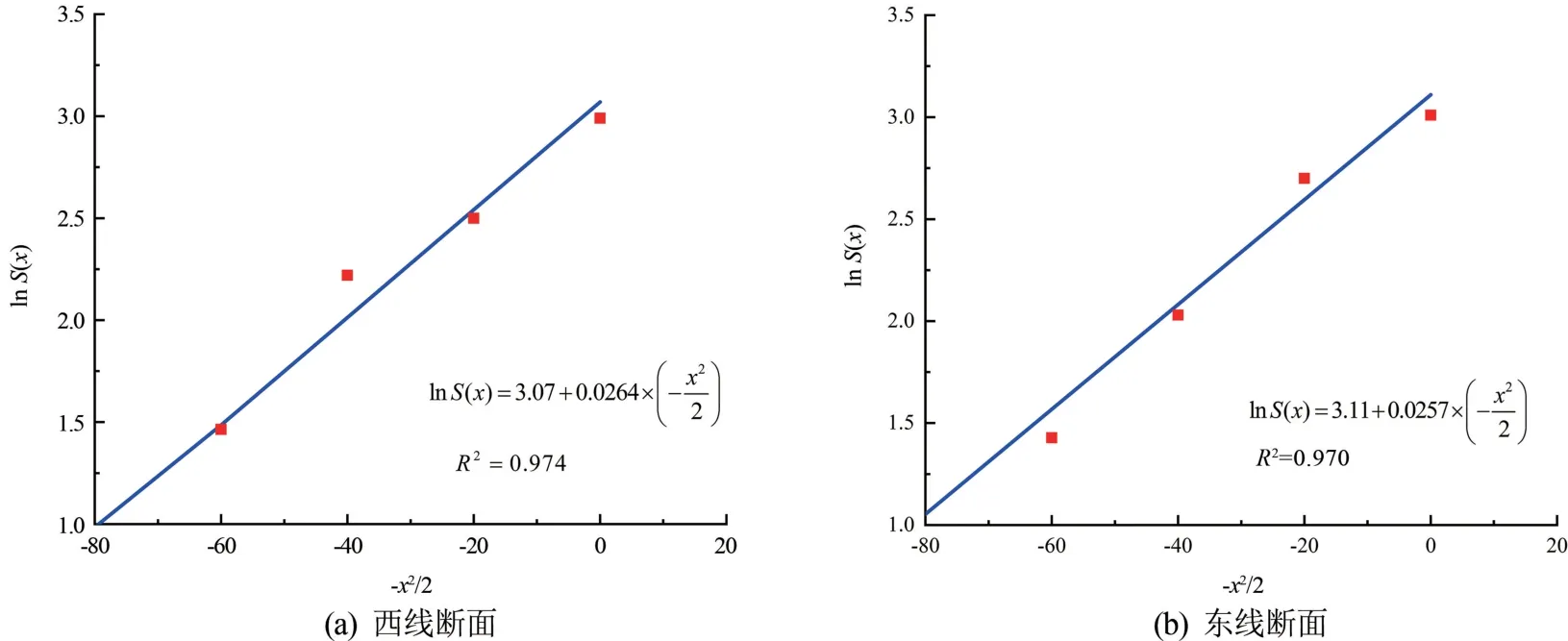
图11 东、西线断面回归分析图

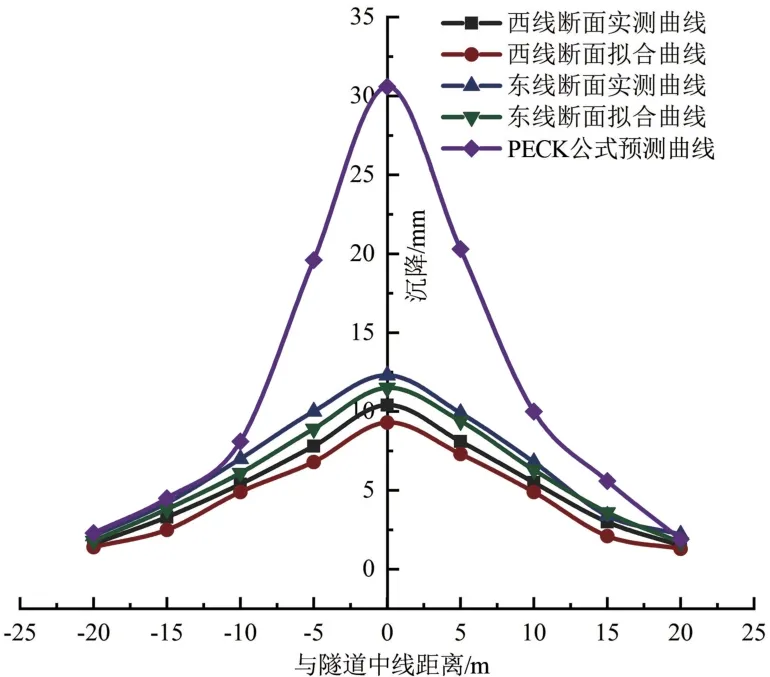
图12 东西线拟合曲线结果与PECK公式直接预测对比图

4.3 引入系数λ、γ修正PECK公式

由4.2节可知，PECK公式无法精确预测盾构穿越黄河地层时的沉降，故需要结合实际工程概况引入地表最大沉降值修正系数λ和沉降槽宽度修正系数γ[10]，修正后公式由式(8)表示为

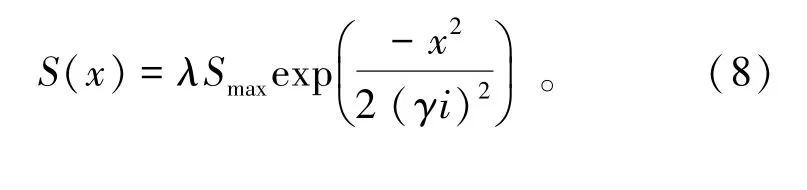
对公式两边同时取对数进行回归分析，得到

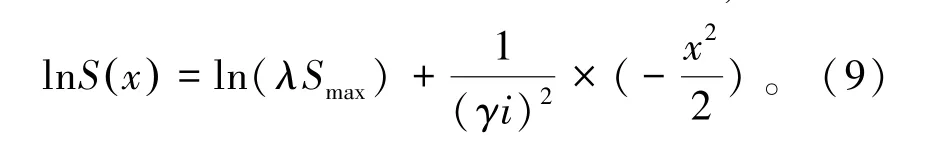
通过式(6)、(7)和(9)求得λ和γ，分别由式(10)和(11)表示为

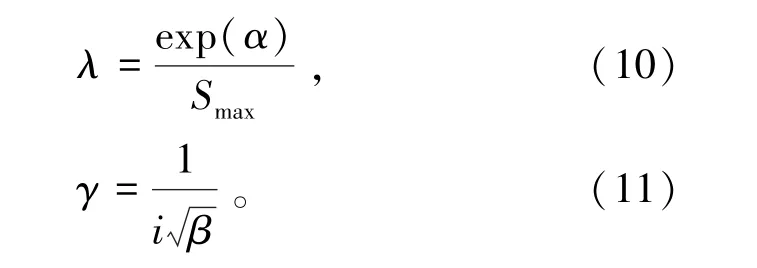
结合工程实际数据，式(10)和(11)中的沉降槽i与Smax根据式(2)～(4)求解得到i＝22.99 m、Smax＝32.3 mm。

确定λ、γ的取值范围时，若只研究DK2+0断面，结果并无代表性。通过整理对盾构机穿越黄河浅滩过程中24个断面监测数据，求得各断面回归方程的常数项α以及回归方程的线性系数β；根据式(10)和(11)确定各断面的λ、γ值，将所有断面求得的λ、γ值，放入样本集合，确定λ、γ值分布最广区间如图13所示，系数λ在0.43～0.76中的占比达到85%，系数γ在0.18～0.42中的占比为80%。该模型在后续黄河中下游地区修建穿黄河隧道工程进行沉降预测时，根据沉降槽与最大沉降量的一般关系，选取沉降槽宽度最大、最大沉降最小时的曲线作为修正后PECK公式预测沉降的下限曲线，此时λ＝0.76、γ＝0.18；选取沉降槽宽度最小、最大沉降量最大的曲线作为修正后PECK公式预测沉降的上限曲线，此时λ＝0.43、γ＝0.42。

图13 修正系数取值图

4.4 验证修正后的PECK公式曲线模型

整理盾构施工期间在始发井和接收井有角度下穿阶段18个断面的监测数据，并代入修正后PECK公式上、下限曲线内，验证修正后PECK公式预测结果的准确性(如图14所示)。虽然有个别实测数据大于或小于预测曲线区间，但是沉降数据中分布最广区间(约92%)依然落在了预测曲线上下限内。说明修正后的PECK公式模型可以很好地预测盾构穿越黄河中下游软土地区的沉降。

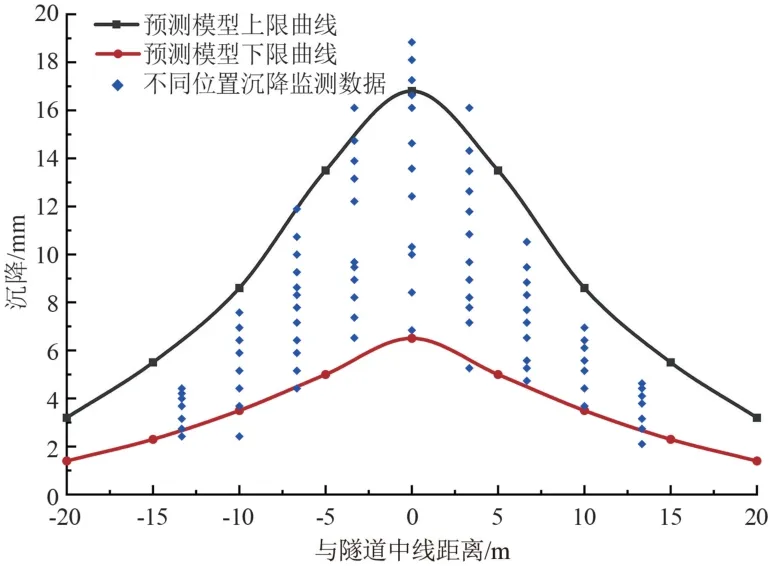
图14 实测数据与修正后PECK公式预测曲线对比图

5 结论

结合济南黄河隧道工程盾构施工数据，研究了盾构施工对土体位移以及应力变化的影响，模拟分析了盾构施工过程中黄河地层的一般变形规律，修正了典型PECK公式沉降预测模型使其适合预测黄河中下游软土地区的沉降。得到主要结论如下:

(1)地层沉降槽宽度的变化以及最大沉降位置与PECK公式模型预测吻合。根据每一阶段土层的影响程度和方式的不同，施工中提前做好控制地层稳定的措施，如超前加固、同步注浆等。

(2)隧道上部土体在开挖后未支护的阶段，应力释放严重，产生的沉降最大。随着衬砌支护逐渐完成，衬砌的支护力作用于土体，沉降云图开始向掌子面上方移动。通过对比有限元模拟结果与施工监测数据，发现二者吻合较好，表明有限元法可以很好地预测盾构开挖对黄河地层的沉降影响。

(3)引入沉降槽宽度修正系数、最大沉降量修正系数，修正典型PECK公式模型，得到沉降预测曲线。通过分析18个断面的沉降情况，发现92%的监测数据分布在上、下限曲线内。故证明修正后的PECK公式能够很好地预测盾构穿越黄河中下游软土地层的沉降情况。