Ac Josephson effect in Corbino-geometry Josephson junctions constructed on Bi2Te3 surface

Yunxiao Zhang(张云潇) Zhaozheng Lyu(吕昭征) Xiang Wang(王翔) Enna Zhuo(卓恩娜)Xiaopei Sun(孙晓培) Bing Li(李冰) Jie Shen(沈洁) Guangtong Liu(刘广同)Fanming Qu(屈凡明) and Li L¨u(吕力)

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

4Hefei National Laboratory,Hefei 230088,China

Keywords: Corbino-geometry Josephson junction, topological insulator, ac Josephson effect, fractional Shapiro steps

1. Introduction

Majorana zero modes(MZMs)are believed to obey non-Abelian exchange statistics, a preparty that can be used for implementing topological quantum computing.[1–4]It is predicted that MZMs exist at the boundaries of p-wave superconductors or p-wave-like hybrid superconducting systems,the latter are composed of s-wave superconductors and the materials with strong spin–orbit coupling such as topological insulators,[5]certain semiconductor nanowires,[6–8]etc.Experimental evidence for the existence of MZMs has been found, including the observations of zero-bias conductance peak,[9–13]complete energy gap closure in line Josephson junctions (JJs)[14]and trijunctions[15]constructed on the surface of Bi2Te3, skewed current-phase relation (CPR),[16]etc.But the braiding operation of MZMs is yet to be realized.

Among various schemes for hosting and braiding MZMs,the one proposed by L.Fu and C.L.Kane in 2008 using topological insulator-based JJs has the advantages in simplicity and scalability,[5]i.e., no additional magnetic field is needed to drive the system into the topologically-nontrivial regime,and the number of qubits can be scaled up in two dimensions via surface coding.[17]Within the Fu–Kane scheme,there is a particular theoretical proposal that is further worthy to investigate—hosting and braiding MZMs in Corbino-geometry JJs constructed on the surface of topological insulators.[18,19]Previously,Corbino-geometry JJs constructed on topologically trivial materials have been studied.[20,21]Due to the Meissner effect and superconducting screening,the magnetic flux entering into the outside ring of the Corbino-geometry JJ is quantized,leading to a magnetic field dependence of critical supercurrent different from the common Fraunhofer pattern of a traditional JJ.By constructing Corbino-geometry JJs on topological materials, besides their advantages in hosting and manipulating MZMs as proposed by the theorists, the noise sector from magnetic field fluctuation, which could have huge impact on the phase coherence time of the qubits, can be shielded. In addition to providing magnetic shielding, the Corbino geometry can also isolate the Andreev bound states (ABSs) of the JJs from the external environment,thereby reducing the quasiparticle poisoning rate to the parity of the quantum states.Given these advantages,Corbino-geometry JJs constructed on the surface of topological insulators might serve as a promising platform for hosting and braiding MZMs, studying their non-Abelian exchange statistics, and for implementing topological qubits.

In this work, we successfully fabricated Corbinogeometry JJs on the surface of Bi2Te3topological insulator.Column-like distribution of critical supercurrent with varying magnetic field, rather than standard Fraunhofer pattern, was observed. When microwave irradiation was added, fractional Shapiro steps appeared on the current–voltage characteristics of the JJs. The results indicate that these Corbino-geometry JJs are highly transparent,with a skewed CPR that is in favor of the existence of MZMs in the devices.

2. Experimental setup

Figure 1(a) shows the false-color scanning electron microscopy image of one of the Corbino-geometry JJs. Two superconducting electrodes made of Al/Ti (80 nm/5 nm) were evaporated to the surface of a Bi2Te3flake of～60 nm in thickness, to define a proximitized superconductor–TI–superconductor JJ in a Corbino geometry. An insulating layer of overexposed polymethyl methacrylate(PMMA)was fabricated to cover the device except for leaving a window on the central electrode of the JJ. Through the window the central electrode was bombardedin situwith argon ions to remove the surface oxide layer,then an additional superconducting Al arm(～100 nm thick)was deposited,realizing superconducting contact with the central electrode. Figure 1(b) illustrates the cross-section view of the device, together with the quasifour-probe electron transport measurement configuration. The measurements were carried out in a dilution refrigerator with a base temperature of～20 mK.

In this paper, we will first present and discuss the magnetic flux dependence of theIJ–VJcharacteristics(IVC)(whereIJis the dc bias current passing through the JJ, andVJis the voltage drop across the JJ).Then,we will present and discuss the data of ac Josephson effect.

Fig.1. (a)False-color scanning electron microscope image of the Corbinogeometry JJ used in this experiment. The radius of the inner electrode Rinner is ～200 nm,the junction length L is ～200 nm,and the width of the outer electrode W is ～300 nm. (b)Illustrations of the cross-section of the device,together with the configuration for differential resistance measurement.

3. Results and discussion

3.1. The Josephson supercurrent in the presence of integer number of flux quanta penetration

First, we measured the differential resistance dVJ/dIJbetween the two superconducting electrodes of the Corbinogeometry JJ as a function of magnetic fieldBand bias currentIJat the base temperature. The result is shown in Fig.2,where the bias currentIJwas swept from the bottom to the top, and the magnetic fieldBwas swept from the left to the right. The white areas in the figure represent the zero-resistance state.The pattern is asymmetric in the vertical direction,due to the existence of hysteresis in the IVC as is commonly seen for JJs constructed on the surface of topological insulators.[14]The envelope of the zero-resistance state forms a series of columns with different heights,when the magnetic field is varied. The period of the pattern is roughly ΔB=23.3±3.1 Gs.

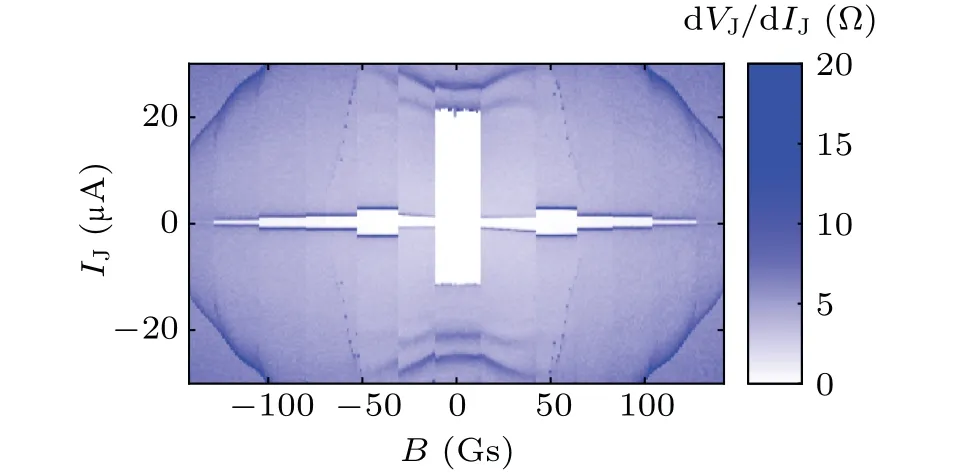
Fig. 2. The measured differential resistance dVJ/dIJ as a function of bias current IJ and magnetic field B. The white areas represent the zero-resistance state, which has a column-like envelope due to quantized flux penetration into the Corbino-geometry JJ.The central column corresponds to zero flux penetration(n=0).The high-n columns correspond to integer number of flux quanta(nφ0)penetration. The non-zero critical supercurrents at high-n columns are caused by the nonuniformity of supercurrent density and phase in the junction.

Due to Meissner screening, the flux penetrated into the junction area from the outer ring of the Corbino-geometry JJ must be quantized,φ=nφ0, wherenis an integer number,φ0=h/2eis the flux quantum with the Cooper pair of charge 2e, andhis the Planck constant. The effective area corresponding to ΔBcan be estimated asSeff=φ0/ΔB=0.89 μm2.This estimated area is in good agreement with the effective area of the outer ring:S=πr2=π×0.552μm2=0.95 μm2,whereris the radius of the outer ring at its half width.

It should be pointed out that the envelope of the zeroresistance areas in Fig. 2 is not consistent with the standard Fraunhofer pattern of a diffusive JJ even after considering flux quantization. Following the conventional mechanism of the Fraunhofer pattern,for an ideal Corbino-geometry JJ the critical supercurrent should be all zero,except for the central column where no magnetic flux is penetrated into the junction area (n=0). We attribute the non-zero critical supercurrent in high-ncolumns (corresponding tonφ0flux penetration) to the nonuniform distribution of the supercurrent density in the junction. The spatial(i.e.,directional)dependence of the critical supercurrent density can be obtained by discretizing the inverse Fourier ransform of the envelope of critical supercurrent versus quantized magnetic flux. The result shows that the spatial nonuniformity of the supercurrent density in the measured Corbino-geometry JJ reaches～9% (see Part I of the supplementary materials for the detailed estimation).

3.2. Ac Josephson effect and fractional Shapiro steps

In the presence of rf irradiation, there will be Shapiro steps on the IVC of a JJ,due to mode-locking between the rf frequency and the Josephson frequency caused by ac Josephson effect. Figure 3(a) shows the dVJ/dIJand the IVC of the JJ measured with microwave irradiation at a frequency off=3.5 GHz(corresponding tohf/2e=7.3 μV)and a power ofPrf=-7.5 dBm. The IVC is obtained by numerically integrating the dVJ/dIJvs.IJcurve. Integer Shapiro steps on the IVC, corresponding to the dips on the dVJ/dIJvs.IJcurve,can be clearly seen. Surprisingly,on the dVJ/dIJvs.IJcurve in Fig. 3(a) there are also small dips between the main dips,leading to the emergence of half-integer steps between the integer ones.

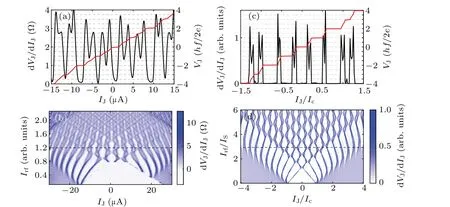
Fig.3. (a)Differential resistance dVJ/dIJ (black curve)of the Corbino-geometry JJ as a function of bias current IJ, measured in the presence of microwave irradiation at a frequency of f =3.5 GHz and a power of Prf =-7.5 dBm. The data are from the linecut in(b)marked by the dashed line. The IVC (red curve) of the junction obtained by numerically integrating the dVJ/dIJ data. The dips on the black curve correspond to the Shapiro steps on the IVC.Not only integer steps but also half-integer steps can be resolved. (b) dVJ/dIJ as a function of dc bias current IJ and rf current Irf at a microwave frequency of f =3.5 GHz. Both integer Shapiro steps(represented by relatively large white blocks)and half-integer steps with twisted knot structures(small white blocks)are clearly visible. (c)The simulated IVC(red)and dVJ/dIJ vs. IJ curve[black,a linecut along the dashed line in(d)]by using the RSJ model and with a skewed CPR containing high harmonic terms of supercurrents. Fractional steps emerge on the curves,supporting that the presence of high harmonic supercurrents in CPR can lead to the emergence of fractional steps. (d)Simulated IJ and Irf dependence of dVJ/dIJ,demonstrating integer and fractional Shapiro steps and the twisted knot structures mimicking those in(b).

To verify that the steps on the IVC are integer and halfinteger Shapiro steps, we measured the microwave frequency dependence of the voltages of the 1stand 2ndsteps.The results are shown in Fig.4(a). The positions of the steps follow a linear law extrapolatable to the origin of the coordinates, with slopes close to 1/2 and 1,respectively,confirming that the 1stand 2ndvoltage steps on the IVC are half-integer and integer Shapiro steps due to ac Josephson effect.

Being Shapiro steps, their positions should not change with microwave powerPrf. In Fig.4(b),we replot the dVJ/dIJdata in Fig.3(b)as a function ofVJandIrf,whereVJis obtained through integrating the dVJ/dIJvs.IJcurves. Now,the white lines in Fig.4(b)correspond to the Shapiro steps. Both integer and half-integer steps can be resolved. While there are small wiggles on the position of the steps,presumably caused by the errors introduced during integrating the discrete data points,the average positions of the steps are power-independent. The discontinuity of the half-integer steps with varyingIrfcorresponds to the twisted knot structures in Fig.3(b).

Now, let us discuss the possible origins of the halfinteger steps. It is well known that the chaotic behavior existed in underdamped JJs may trigger bifurcations and subharmonic mode-locking, thus leading to the appearance of fractional steps,when the Stewart–McCumber parameterβ=4πeR2IcC/his larger than 1,whereRis the junction resistance,Cis the junction capacitance, andIcthe critical supercurrent of the junction. For our Corbino-geometry JJ,the capacitanceC ≈0.1 fF can be estimated via electrostatic field simulations,and the resistanceR ≈4 Ω and critical supercurrentIc≈20 μA can be obtained from the experimental data, so that we haveβ ≈0.971×10-4. In thisβ ≪1 regime,it can be concluded that there will be no chaotic behavior in our device.

Another possible origin of the half-integer steps is associated with the existence of high harmonics in the CPR. In the overdamped limit(i.e.,theβ ≪1 regime),the RSJ model,which describes the behavior of a JJ under microwave irradiation,can be simplified as

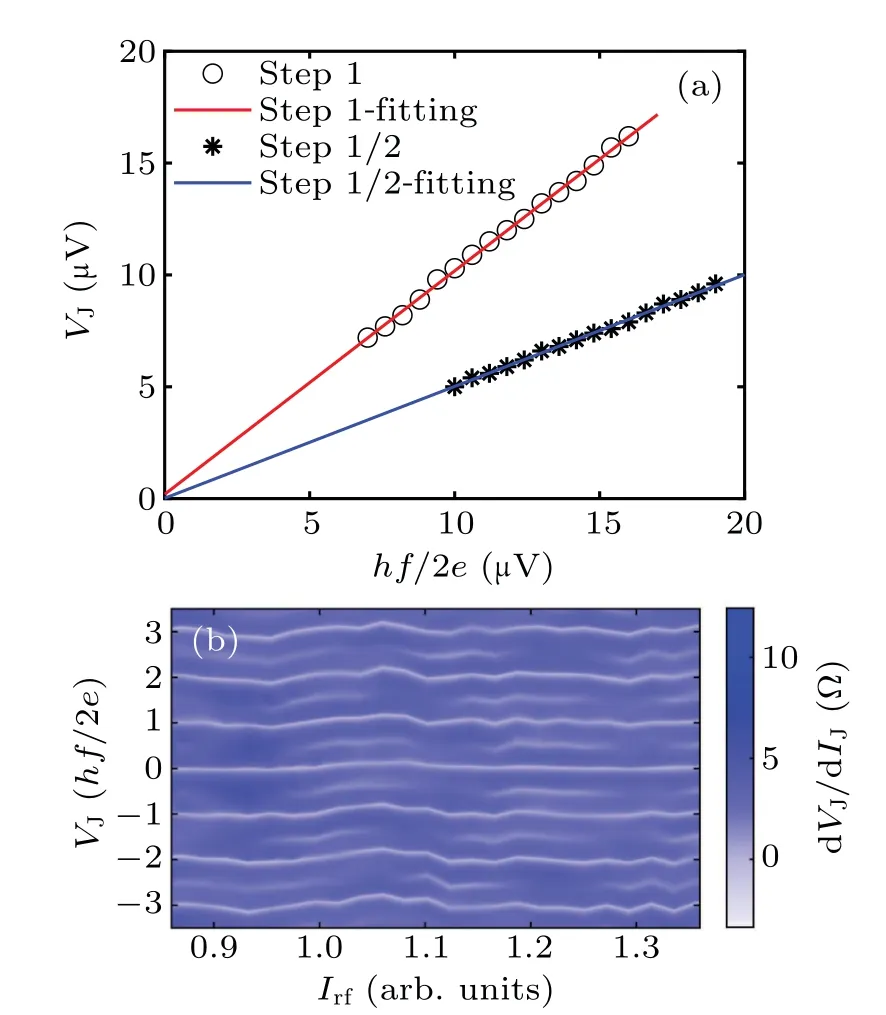
Fig.4.(a)The voltage positions of the 1st step(step 1/2)and the 2nd step(step 1)as a function of microwave frequency hf/2e, demonstrating a linear law extrapolatable to the origin of the coordinates,with slopes of 0.504±0.014 and 1.016±0.027,respectively. (b)Same dVJ/dIJ data as in Fig. 3(b), but plotted as a function of voltage VJ and rf current Irf. The white lines correspond to the Shapiro steps. Both integer and half-integer steps can be resolved.

The appearance of high harmonic terms in CPR is associated with the high transparency of the JJs. According to the theory,[22]the CPR of a JJ is generally a function of the transmission coefficientD:

whereΔis the induced superconducting energy gap of the proximitized JJ.For traditional JJ in the non-transparent limit

which is skewed at low temperatures. By performing discrete Fourier transform on Eq.(3)and takingΔ(T)≈0.2 meV,T ≈20 mK,we can get the CPR of our Corbino-geometry JJ with the first few harmonics:IS(φ)/Ic≈sin(φ)-0.39sin(2φ)+0.25sin(3φ)···. It can be seen that,in addition to the second harmonic term which leads to the half-integer steps as shown in Figs.3(c)and 3(d),there should also have third and higher harmonic terms. The third harmonic term should lead to 1/3 and 2/3 fractional steps between the integer ones. Indeed,evidence for these fractional steps can be found in our data,and is presented in Part II of the supplementary materials.

In the above, we attributed the presence of the fractional Shapiro steps to the high transparency of the Corbinogeometry JJs deposited on the surface of a topological insulator. Usually, the high transparency in proximitized JJ is associated with the high electron mobility in the material that the JJ is constructed, the junctions based on InAs nanowires,[23]graphene[24]and three-dimensional topological insulator HgTe[25]are some examples. In the present experiment, the measured Hall mobility of the electrons in topological insulator Bi2Te3is only～1000 cm2/V·s,[26,27]being much lower than that in the materials mentioned above. A possible explanation for having unusually high transparency is that, there are two types of conduction channels, and accordingly two different CPRs,in the JJ constructed on the surface of topological insulator Bi2Te3. One is the bulk-electron conduction channel with relatively low electron mobility[26,27]as probed by the Hall mobility measurement. The other is the surface electron conduction channel with relatively high electron mobility, due to time reversal symmetry protected suppression of electron backscattering on the surface of topological insulators. The surface channel contributes to the high transparency of the JJ. In fact, the existence of highly transparent surface channel, which leads to a fully skewed CPR and complete minigap closure in JJs constructed on the surface of topological insulators, has already been demonstrated previously.[14,15]

There is one additional reason why the ac Josephson effect with fractional steps is easier to be observed in Corbinogeometry JJs than in traditional line JJs — unlike in line JJs there are two ends which cause dissipations, Corbinogeometry JJs has no such ends,hence being less dissipative.

4. Summary

In summary, we have successfully constructed Corbinogeometry JJs on the surface of topological insulators. We characterized the critical supercurrent of the JJs as a function of magnetic field, and studied the rf current dependence of the IVC. Ac Josephson effect with fractional steps was observed. The results indicate that the CPR of Corbinogeometry JJs constructed on topological insulators is skewed,containing high harmonic terms,supporting that these JJs are highly transparent. The appearance of fractional steps,which are not observed before in line JJs constructed on the same type of topological insulators,are probably benefited from the Corbino-geometry structure, which protects the electrons in the junction area from the electrical dissipation and magnetic noises from the outside. For these reasons, we believe that Corbino-geometry JJs may serve as a promising platform for constructing topological qubits and braiding MZMs in the future.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.92065203,11527806,12074417,11874406, 11774405, and E2J1141), the National Basic Research Program of China (Grant Nos. 2016YFA0300601,2017YFA0304700, and 2015CB921402), the Strategic Priority Research Program B of the Chinese Academy of Sciences (Grant Nos. XDB33010300, DB28000000, and XDB07010100), the Innovation Program for Quantum Science and Technology(Grant No. 2021ZD302600),and Synergetic Extreme Condition User Facility(SECUF)sponsored by the National Development and Reform Commission,China.