丁坝挑角对弯道水流流态影响的模型试验研究

温文杰

(茂名市鉴江流域水利水电建筑安装工程有限公司,广东 茂名 511500)

1 概述

自然界中的河流由于受到地形、地质等诸多自然条件的影响，其流向和边界会不断变化，最终导致弯曲型河道成为河流中的最常见形态[1]。弯道中的水流在重力和离心力的共同作用下，会在横断面上形成断面环流，同时和纵向水流相互作用形成弯道所特有的螺旋流[2]。这种特殊的水流结构会造成河流弯道的凹岸部位的冲刷和凸岸部位的淤积，从而对河岸的稳定性造成十分显著的影响[3]。丁坝作为河道整治工程中最常见的一种建筑物，坝前水流的流速在其阻水作用影响下会迅速减小，流动方向也会远离凹岸，从而实现坝后弯道水流方向与形态的重布，有效缓解凹岸冲刷和凸岸淤积的现象，具有良好的工程应用价值[4]。丁坝上述作用的发挥和丁坝的设计参数存在密切关系，在丁坝的设计和建设中需要根据工程现场的实际情况，对丁坝的数量、长度、位置以及挑角等参数进行合理设计[5]。基于此，本文以180弯道为例，将丁坝的挑角作为研究变量，利用室内模型试验的方式探讨挑角这一参数对弯道水流流态的影响，以便为相关理论研究和工程设计提供必要的支持和借鉴。

2 模型与试验方法

2.1 试验模型

试验模型以某河流弯道为工程背景设计，该弯道的上游直水槽长为16m，弯道中心线的半径为2m，下游直水槽的长度为16m。过流断面的尺寸为0.8m×0.8m。变坡范围为0～1%，弯道中心角为180°。试验模型利用有机玻璃板制作。按照SL 155—2010《水工(常规)模型试验规程》中的相关规定，整体模型的平均误差需要控制在10mm以内，地形高度误差不得大于2mm，漏水量不能超过试验过水量的1%。在模型制作过程中严格按照上述规定制作，并多次使用水平仪进行校平[6]。试验中所使用的丁坝模型为15cm×2cm×40cm，材料为普通有机玻璃，丁坝模型紧贴水槽边壁置于弯道的凹岸部位。

试验模型的流量控制系统由数字式智能硬件和软件系统组成。其中，硬件系统主要由计算机、控制箱、蓄水池、电磁流量计、水泵以及尾门自动控制箱等组成，软件部分为JFC2017系统，在系统开机之后，可以通过手动增减变频器运行频率的方式控制水泵的转速和出水量，同时通过尾门开度调节，实现对尾水位的精准控制。

2.2 试验方法

为了获取丁坝挑角对弯道水流的影响，在模型试验过程中设置14个测量断面，其均匀分布于弯道的前130°，相邻2个测量断面之间的夹角为10°，断面从上游至下游编号，分别为D1—D14。在试验水槽的相关部位设置有自动水位测量系统，该系统主要由无线超声波自动水位测量计、自动水位测量系统和控制箱采集程序组成[7]。

2.3 试验方案

此次研究的主要目的是探讨丁坝挑角对弯道水流流态的影响，结合相关工程经验和研究目的，设置45°、60°、75°、90°、105°、120°和135°等7种不同的挑角进行试验[8]，见表1。

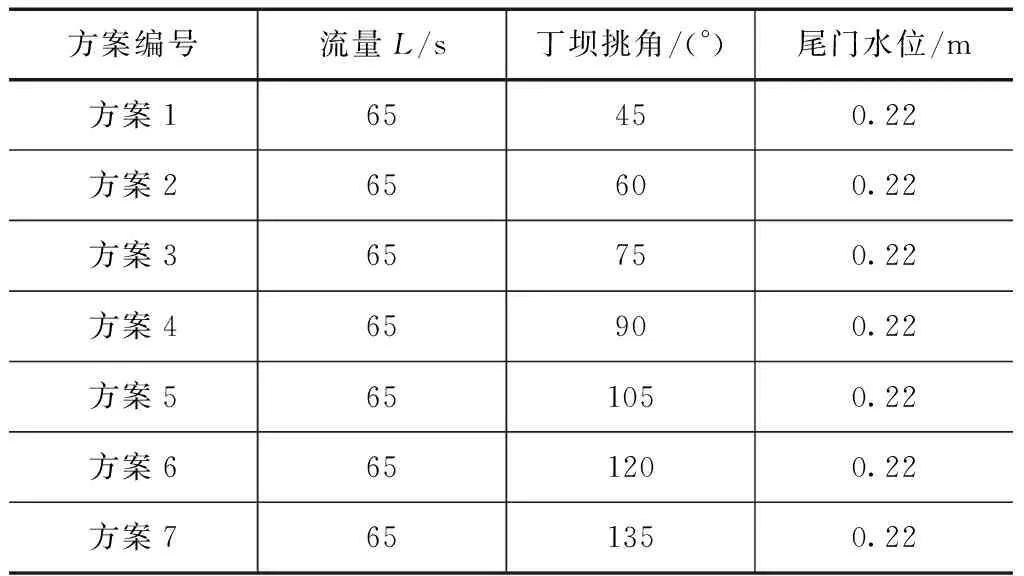
表1 计算方案参数设计

3 计算结果与分析

3.1 沿程水位

根据试验中获得的水位数据，计算获取关键断面的水位值和所出现的断面位置，见表2。根据表2中的数据，绘制出水位值随丁坝挑角的变化曲线，结果如图1所示。由表2和图1可以看出，不同试验方案条件下弯道水位的沿程分布规律基本相似，特别是水位的最高点和最低点出现的部位基本一致。但是，对于不同的丁坝挑角设计方案，其水

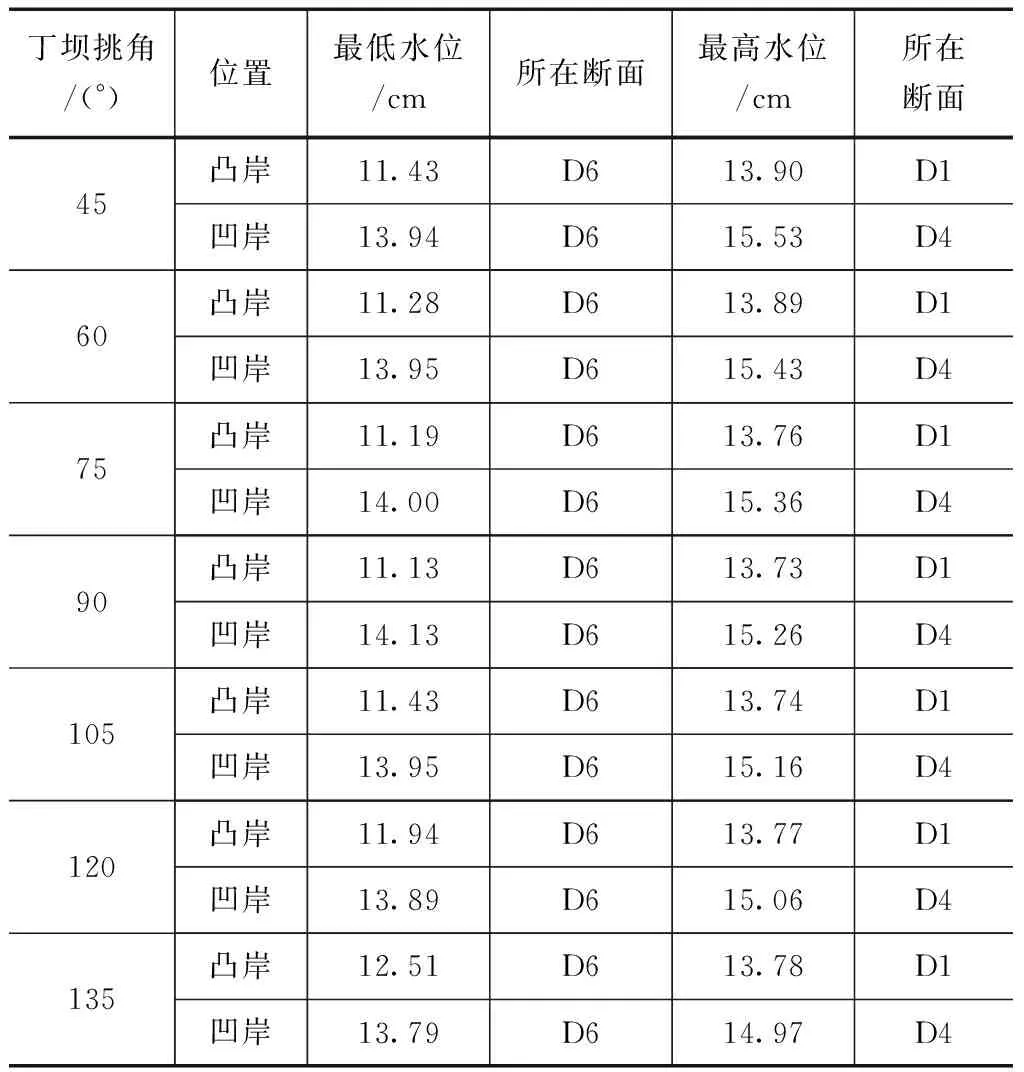
表2 不同方案水位极值及所在断面计算结果

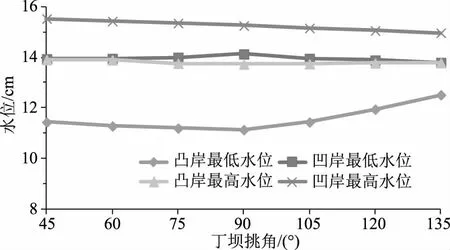
图1 水位极值变化曲线

位的变幅方面仍存在一定的不同。首先，随着丁坝挑角的增大，弯道的最低水位呈现出先下降后上升的变化趋势，水位的最低点出现在丁坝挑角90°方案；其次，弯道的最高水位与最低水位的变化规律类似，也随着丁坝挑角的增大呈现出先减小后增大的变化特点。由此可见，丁坝挑角为90°时弯道水流的最高与最低水位差最大；丁坝挑角为135°时弯道水流的最高与最低水位差最小。在凹岸，随着丁坝挑角的不断增大，弯道水流的最低水位呈现出先增大后减小的变化趋势，但是变化幅度相对较小；最高水位的变化则呈现出不断减小的变化趋势，丁坝挑角为45°时的水位变化相对最大，而135°挑角丁坝的水位沿程变化相对较小。

3.2 沿程水面横比降

水面横比降在弯道水力特征研究中具有重要意义，如果该值过大，就会造成弯道段河床的巨大破坏，对船只的通行也会造成比较严重的负面影响。研究中根据试验数据，计算获取各个监测断面的横比降最大值和最小值，结果见表3。根据表3中的结果，绘制出最大横比降随丁坝挑角的变化曲线，结果如图2所示。由表3和图2可知，不同挑角的丁坝对断面的水面横比降的影响存在一定的差别，但是在整体变化趋势上又有一定的相似性和共性特征。其中，水面横比降的最大值均位于D3断面部位，随着丁坝挑角的增大，水面横比降呈现出不断减小的变化趋势，且减小的幅度也不断增大。

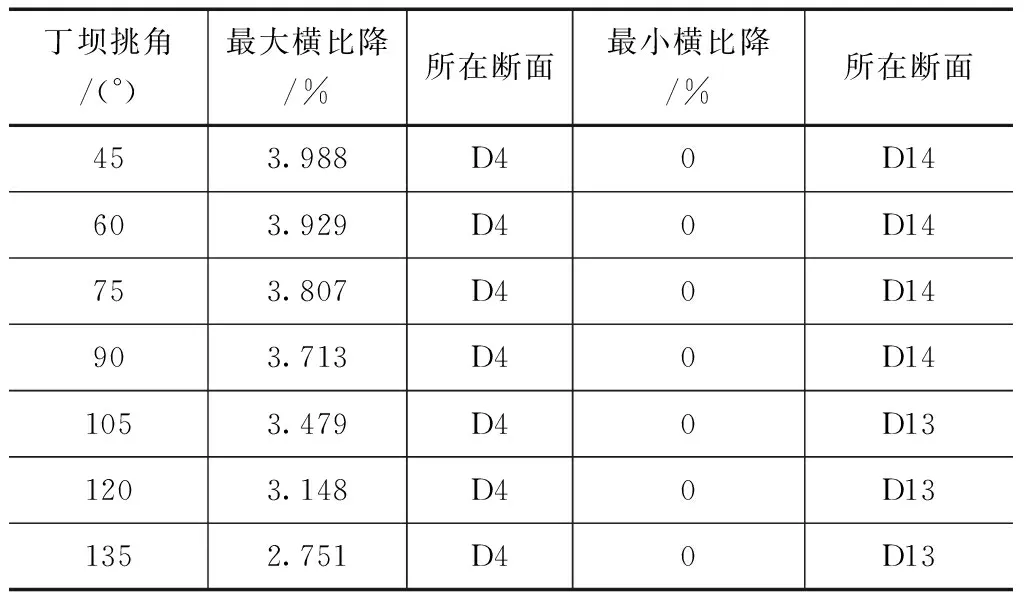
表3 不同方案沿水面横比降极值及所在断面计算结果

图2 最大横比降变化曲线

3.3 沿程水面纵比降

沿程纵比降也是弯道水流流态研究的重要参数，纵向水流流速会随着纵比降的增大而减小。研究中根据试验数据计算获取水面纵比降，结果见表4。根据表4中的数据绘制出沿程纵比降随丁坝挑角的变化曲线，结果如图3所示。由表4和图3可以看出，不同丁坝挑角试验方案的最大纵比降和最小纵比降出现的部位基本一致，但是计算结果存在一定的差异。具体来看，随着丁坝挑角的增大，凸岸的最小纵比降呈现出先减小后增大的变化趋势，而最大纵比降呈现出先增大后减小的变化趋势，变化幅度明显偏大；凹岸的最小纵比降呈现出不断减小的变化特征，最大纵比降则呈现出先小幅减小后趋于稳定的变化特点。

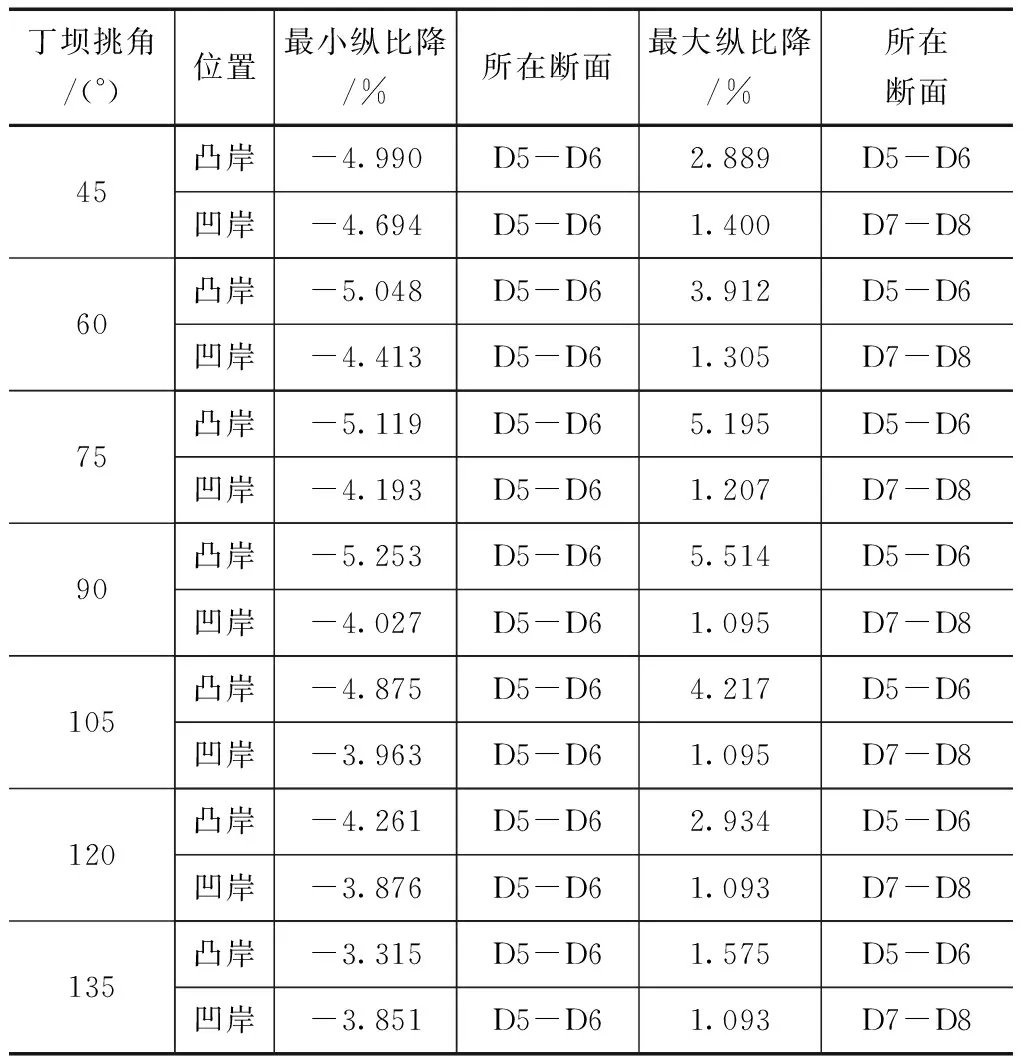
表4 不同方案水面纵比降极值及所在断面计算结果

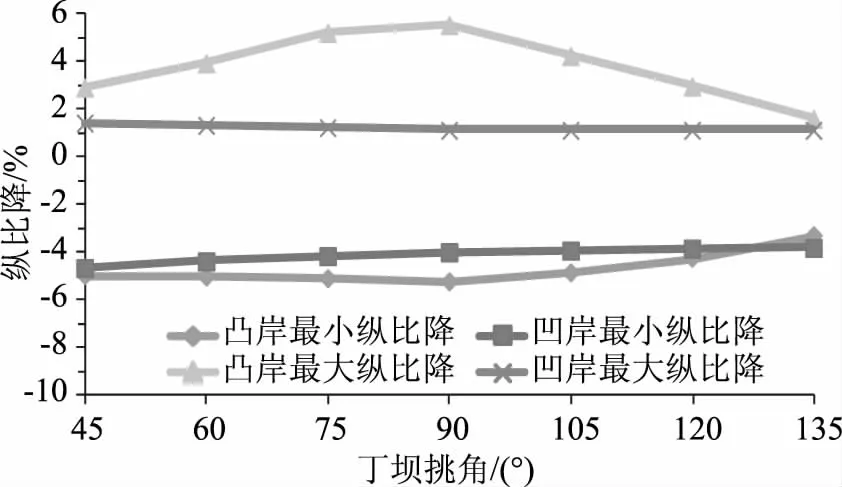
图3 纵比降变化曲线

4 结语

此次研究通过模拟计算的方法，探讨了不同丁坝挑角对弯道水流流态的影响，并获得相应的变化规律，认为挑角为135°时的整体流态较好，推荐在工程设计中使用。研究成果不仅对相关的理论研究起到重要支撑和完善作用，对丁坝的工程设计和应用也具有重要的借鉴意义。当然，受到诸多因素的影响和制约，此次研究在方法和内容方面仍存在诸多欠缺和不足，需要在多方面进行进一步的改进和补充。此次研究对水流的边界设置均为理想条件，而天然河道的水流特征更为复杂，影响因素更多，因此有机会可以在天然河道上进行现场试验，以便对理论计算结果进行对比和论证，提高研究结果的科学性和价值。