Distributed Cooperative Learning for Discrete-Time Strict-Feedback Multi Agent Systems Over Directed Graphs

Min Wang,, Haotian Shi, and Cong Wang,

Abstract—This paper focuses on the distributed cooperative learning (DCL) problem for a class of discrete-time strict-feedback multi-agent systems under directed graphs. Compared with the previous DCL works based on undirected graphs, two main challenges lie in that the Laplacian matrix of directed graphs is nonsymmetric, and the derived weight error systems exist n-step delays. Two novel lemmas are developed in this paper to show the exponential convergence for two kinds of linear time-varying(LTV) systems with different phenomena including the nonsymmetric Laplacian matrix and time delays. Subsequently, an adaptive neural network (NN) control scheme is proposed by establishing a directed communication graph along with n-step delays weight updating law. Then, by using two novel lemmas on the extended exponential convergence of LTV systems, estimated NN weights of all agents are verified to exponentially converge to small neighbourhoods of their common optimal values if directed communication graphs are strongly connected and balanced. The stored NN weights are reused to structure learning controllers for the improved control performance of similar control tasks by the“mod” function and proper time series. A simulation comparison is shown to demonstrate the validity of the proposed DCL method.

I. INTRODUCTION

OVER the past three decades, fuzzy logic systems (FLSs)[1] and neural networks (NNs) [2] have been generally used to model nonlinear smooth functions due to their inherent features including universal function approximation, online learning, and system identification. By combining FLSs/NNs with the adaptive technology and backstepping method, a large number of adaptive neural or fuzzy control strategies have been proposed for nonlinear systems with unknown dynamics in continuous-time domain, see [3]–[8]and the references therein. Subsequently, a few adaptive neural or fuzzy control methods have been proposed for discretetime nonlinear systems in a normal form [9], [10], in which system uncertainties only appears in the control channel.However, it is extremely difficult to extend the existing continuous-time schemes to discrete-time high-order nonlinear systems in a low-triangular form, such as strict-feedback and pure-feedback, in which the uncertainties appear in all system dynamical equations. The main reason lies in that the future states are likely to appear in the virtual/actual control laws if directly employing the existing continuous-time schemes,which may lead to the non-causality problem. To overcome such a problem, some systematic frameworks have been developed, including then-step ahead predict method[11]–[13], the dynamical NN predict method [14], and the backstepping-based variable substitution method [15], [16].These control methods have successfully verified the stability of closed-loop systems by Lyapunov theory and have also been applied to many practical systems, such as unmanned vehicles [17], [18], robotic manipulators [19], [20], and synchronous motors [21].

Notice that these methods mentioned above focus on the universal approximation property of NNs and FLSs, in which their learning ability is not a major concern. The so-called learning ability mainly involves knowledge acquisition from past experience and knowledge utilization for improved control performance [22]. However, these aforementioned intelligent control methods cannot ensure the exponential convergence of NN/FLS weights, so, for the repeated same control task, NN/FLS weights still need to be adjusted online. In this sense, the learning ability of these intelligent control schemes is very limited. As we know, learning ability should be a primary consideration for highly autonomous automated systems. However, the learning problem is a great challenge because the persistent excitation (PE) condition of NN is too harsh to be verified in the closed-loop adaptive control systems [23]. To handle such a problem, deterministic learning(DL) has been discussed in [24] for continuous-time nonlinear systems with a normal form. It has been shown in [24], for radial basic function (RBF) NN constructed on regular lattices, regressor sub-vector of the RBF NN satisfies the PE condition if NN inputs are recurrent, which is called the partial PE condition. By using an exponential stable lemma of linear time-varying (LTV) systems and the partial PE condition, NN weights have been proven to converge to small neighbourhoods of their optimal values. Then, these convergent NN weights can be reused to construct the learning controller for the same or similar control tasks. Owing to the advantages of DL, a large number of DL-based control schemes have been reported for many continuous-time systems with complexity structures [25], [26], and been successfully applied to various kinds of practical plants [27]–[30].Compared with a large number of results on the continuoustime case, there are relatively few corresponding results for the discrete-time counterpart due to some essential challenges.So far, only two DL schemes are usable for discrete-time systems in a norm form [27], [28].

It should be noticed that the DL-based learned knowledge only comes from its own signal trajectory experienced. Such a learning ability should be generalized for multi-agent systems due to the cooperation and communication among agents[31]–[34]. As one of the representatively distributed cooperative control strategies, the consensus control [35] is to design a distributed cooperative control law by information interaction between agents, such that all agents reach consensus.Motivated by the DL theory [24] and the consensus theory[36], distributed cooperative learning (DCL) has been proposed in [37] for discrete-time multi-agent systems with a normal form under undirected communication networks, which further enlarged the collaborative learning ability of RBF NN by sharing its NN weights with its neighbors. By establishing a distributed cooperative NN weight updating law and employing a cooperative PE condition, all NN weights will converge to small neighbourhoods near their common optimal values. Due to the shared NN weights knowledge among agents, the DCL-based learned knowledge comes from the union of all agent’s trajectories. From this perspective, DCL has better learning generalization and fault tolerance abilities than DL [24], [27], [28]. Recently, DCL has been extended to nonlinear systems with different complexities including continuous-time nonlinear systems [38], the event-based strategy[39], prescribed performance [40]. In addition, DCL has been also extended to some practical applications, such as multi robot manipulators cooperation [41] and multiple autonomous underwater vehicles formation [42].

It is worth noting that all existing results [37]–[42] on DCL for multi-agent systems have two implicit assumptions that: 1)the considered discrete-time multi-agent systems subject to a normal form; and 2) communication networks are undirected.On one hand, most practical multi-agent systems are impossible to be modeled by discrete-time nonlinear systems with a normal form. Compared with such a special form, the strictfeedback form is more general. Unfortunately, it is difficult to extend the existing DCL results to discrete-time strict-feedback nonlinear systems. The main reason lies in that the NN weight error system is described as a class of LTV systems with time delays. There are no exponential stability results for the time-delay LTV systems, thereby difficultly verifying the convergence of the estimated NN weights for discrete-time strict-feedback systems. On the other hand, undirected networks are sometimes too rigorous because the communication networks may be directed in practice, such as world wide web and mobile broadcast networks [43]. Compared with undirected networks, directed ones show many advantages,such as the less occupation of communication resources and the lower cost of sensors [44], [45]. From a methodological viewpoint, directed networks give rise to some new challenges. Specifically, the existing DCL methods rely heavily on that the Laplacian matrix is symmetric and semi-definite,which can be generated by undirected graphs. Such a matrix makes NN weight error system derived by DCL be transformed into the classical LTV system in DL. Whereas, as shown in [38], directed graphs lead to nonsymmetric Laplacian matrices, which make it extremely challenging to verify the convergence of NN weights of all agents due to the lack of stability theory of LTV systems. As a consequence, it is nonetheless an open and challenging problem to study the DCL problem for discrete-time strict-feedback multi-agent systems over directed graphs.

Motivated by the identified challenges, this paper concentrates on the DCL problem for a group of discrete-time strictfeedback multi-agent systems under strongly connected and balanced directed graphs, in which system dynamics are identical but their tracking signals are different. Firstly, two extended sufficient conditions of exponential convergence are developed for two classes of LTV systems with nonsymmetric matrices orn-step delays. Subsequently, a distributed cooperative control scheme is proposed to ensure the tracking performance of all agents for different reference trajectories by constructing cooperative NN weight updating laws. For the steady-state control process, NN weight error systems are verified to satisfy two extended exponential convergence conditions, so that NN weights of all the multi-agent systems converge to small neighbourhoods near their common optimal values. The convergent NN weights are stored as experience knowledge, which can be reused to construct learning controllers for the same or similar control tasks by the “mod”function. The contributions of this paper are summarized as follows:

1) A novel lemma is proposed to show sufficient conditions on exponential convergence for a class of nonsymmetric LTV systems by the properties of matrix null-space. The lemma generalizes the stability result for classical LTV system with a symmetric system matrix, and serves as the key condition to achieve DCL over directed graphs.

2) An extended stability result is given to show the exponential convergence of a class of discrete-time time-delay LTV systems. Such a result reveals the system state exponentially converges to a sequence rather than a fixed value. Based on this extended result, the convergent NN weights are stored by a set of common optimal series, and the unknown system dynamics are expressed by combining the stored weights and the “mod” function.

3) A novel DCL scheme is proposed for discrete-time strictfeedback multi-agent systems under strongly connected and directed balanced graphs, which not only breaks through the bottleneck of DCL on undirected graphs and the normal structure, but also develops two new exponential stability results,thereby promoting the development of other corresponding fields.

Notations: This paper adopts some standard notations. R,Rm, and Rm×nstand for the set of real numbers, the set ofm×1 real vectors, and the set ofm×nreal matrices;Z+denotes the set of positive integer;Imis am×midentity matrix; 1mis am×1 column vector of all ones;cmis anym×1 constant column vector; ‖·‖ is the 2-norm of a vector;⊗denotes the Kronecker product. λmax(·) is the maximum eigenvalue of a matrix. The subscripts (·)ζand (·)ζ¯stand for the regions close to and far away from φ(Z(k)) , whereφ(Z(k))stands the trajectory composed ofZ(k).A:=Bmeans thatAis denoted asB.

II. PROBLEM FORMULATION AND PRELIMINARIES

A. Problem Formulation

Consider a group of discrete-time strict-feedback multiagent systems, whose form is

Remark 1:Assumption 1 is a common assumption for adaptive control systems to ensure controllability, which can be satisfied by many practical systems, such as underactuated surface vessels [17], hypersonic vehicles [18], and robotic manipulators [19]. The recurrent trajectories [24] include a large category of trajectories, such as periodic, quasi-periodic,and almost-periodic trajectories, which can be used as desired tracking tasks of autonomous vehicles. These directed graphs[46] under Assumption 3 include two important classes of information topology: undirected connected graphs and cyclic graphs, which are widely used to handle consensus and formation control of multi-agent systems.

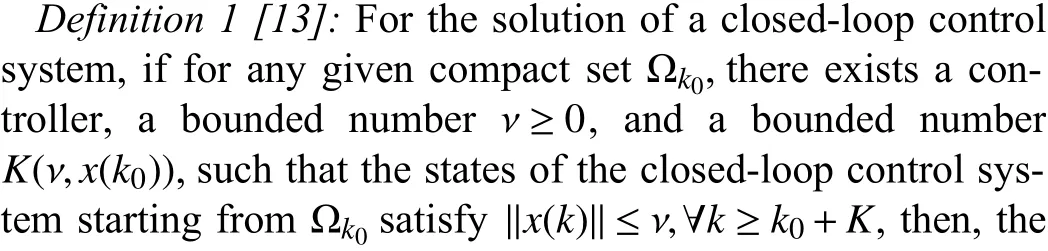
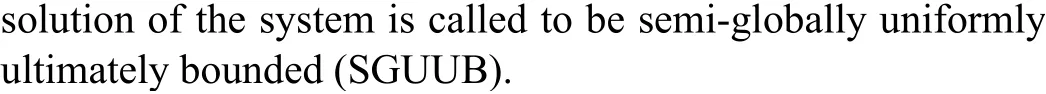
2) The estimated NN weights of all multi-agent system converge to small neighbourhoods around their common optimal values, i.e., each agent can accurately learn and identify the system nonlinear dynamics along the union of the NN input trajectories of all the agents.

Remark 2:It is worth noting that, for discrete-time multiagent systems, the sole DCL scheme was proposed in [37] for a group of discrete-time systems with a normal form subject to the undirected connected graph. In reality, many practical plants can not be characterized as the normal form, such as robotic manipulators, unmanned aerial vehicles, and the chemical reaction systems. Moreover, the undirected graph greatly raises the communication burden. To solve these problems, this paper tries to develop a novel DCL scheme for discrete-time strict-feedback multi-agent systems over strong connected and balanced directed graphs. It should be pointed out that the undirected connected graph can be regarded as a special kind of strongly connected and balanced directed graph [46], which means that the proposed DCL scheme is suitable for more general communication topologies. The successful exploration will enrich the DCL theory, thereby expanding the application areas of DCL.

B. Algebraic Graph Theory

C. Persistent Excitation and Cooperative Persistent Excitation

Remark 3:Lemma 2, proposed in [37], establishes the relationship between cooperative PE and PE under any undirected connected graphs. To achieve the cooperative learning over a directed graph, this paper proposes Corollary 1 to show the effectiveness of this relationship on any strongly connected and balanced directed graph. This extension is a vital of significance to verify the convergence of NN weights for multi-agent systems over a directed graph.

D. RBF Neural Networks

III. ExPONENTIAL STABILITy OF ExTENDED DISCRETE-TIME LTV SySTEMS

Consider the discrete-time LTV system as follow:

Remark 4:Lemma 4 is a fundamental one in the sense that it describes the stability property of a class of LTV systems,which is widely used in adaptive control and adaptive identification fields to verify the convergence of estimated parameters. Lemma 4 has been used to deal with DCL problems for multi-agent systems on an undirected connected graph[37]–[39]. Such a graph can guarantee weight error systems to satisfy the condition of Lemma 4 by using the symmetry of the Laplacian matrix. However, when the graph is directed,Lemma 4 is no longer applicable due to the nonsymmetric Laplacian matrix. To solve this thorny problem, Lemma 7 is proposed in the paper to show a novel exponential stability condition for a class of nonsymmetric LTV systems, which can be used to deal with the DCL problems under strongly connected and balanced graphs. Moreover, it is clear that Lemma 4 is a special case of Lemma 7.

Unlike multi-agent systems considered in [37], this paper focuses on the multi-agent systems with the strict-feedback form, which is more general than that used in [37]. Such a strict-feedback form introducesn-step delays in adaptive updating laws of NN weights. To establish the convergence of NN weights, a new kind of lemma is proposed to show the exponential stability of a class of discrete-time LTV systems withn-step delays.

Lemma 8:Consider the following discrete-time LTV system withn-step delays:

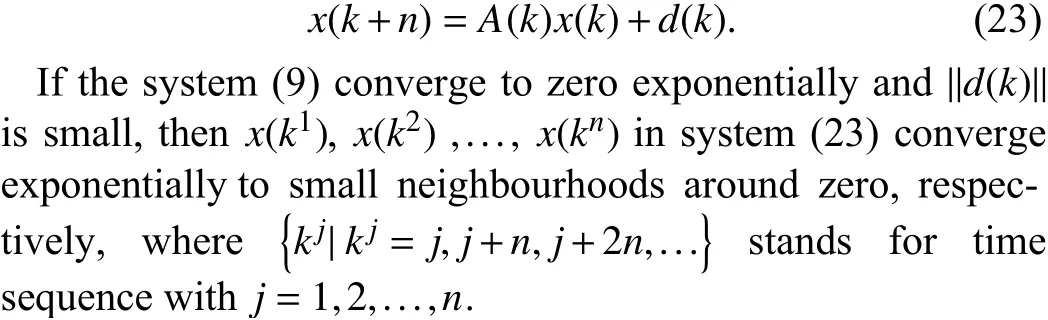
IV. DISTRIBUTED COOPERATIVE LEARNING FROM ADAPTIVE NN CONTROL

In this section, we focus on the DCL problem from adaptive NN control of discrete-time strict-feedback multi-agent systems over a directed graph under Assumption 3.

A. Distributed Controllers Design for Multi-Agent System

To avoid the causality contradiction, then-step predictor method [13] is employed to convert thei-th follower (1) into

B. Stability Analysis of Distributed Cooperative Control

Using Lemma 1, define the initial compact set ΩZi1as:

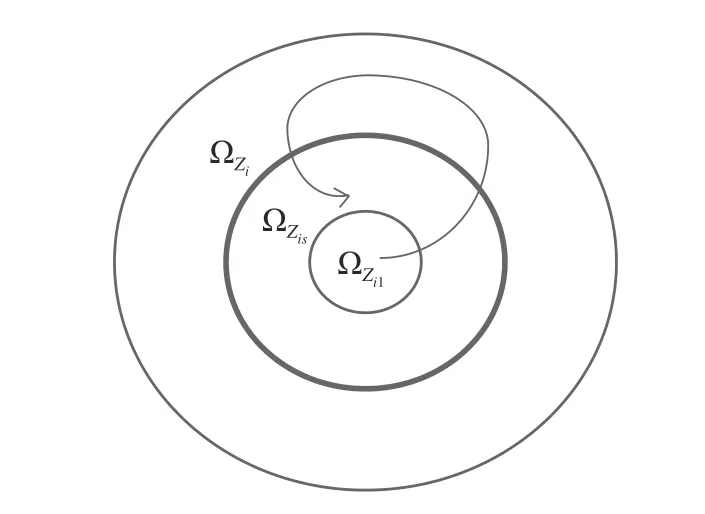
Fig. 1. Three compact sets Ω Zi1, Ω Zis and Ω Zi.

C. Exponential Convergence of RBF NN Weights and Accurate Identification of System Dynamics

Although we have proven the boundness ofST(k)W˜(k) in Theorem 1, the convergence of RBF NN weightsW˜(k) is not enough investigated. In this part, some efforts are devoted to discussing the convergence ofW˜(k) by Corollary 1, and Lemmas 6–8.

Remark 7:It is worth noting that the existing DCL result for discrete-time system [37] has two implicit constraints: the communication network is undirected; and the structure of multi-agent systems satisfies the normal form. To remove the two constraints, this paper takes three specific efforts to deal with DCL for discrete-time strict-feedback multi-agent systems over a strongly connected and balanced directed graph:1) Lemma 7 is proposed in this paper to remove the positive semi-definite and symmetric conditions of system matrixH(k)on the existing exponential convergence of LTV system (9),thereby extending DCL to a class of directed graph by means of some properties of matrix null-space; 2) Lemma 8 is proposed in this paper to show the features on the exponential convergence of LTV system with time delays, thereby showing that estimated NN weightsWˆi(k) for discrete-time strictfeedback multi-agent systems converge exponentially to a set of common optimal seriesW*(kp), instead of a fixed valueW*(k); 3) the knowledge of system nonlinear dynamicsh(Zi(k))is effectively expressed in (48) by the stored NN weights (46) and the “mod” function (47).

D. Learning Control Using Stored Constant NN Weights

V. SIMULATION STUDIES

In this section, a numerical example is given to illustrate the validity of the proposed DCL method. Consider the following four discrete-time agents [12]:

Fig. 2. Communication topology G.

A. Simulation Results of DCL Method

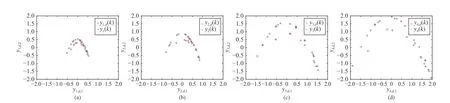
Fig. 3. Tracking performance by DCL in system steady process [ 19971-20000]: (a) agent 1; (b) agent 2; (c) agent 3; and (d) agent 4.

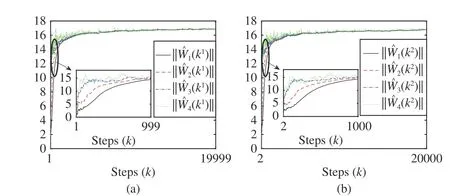
Fig. 4. NN weights ‖ Wˆi(k1)‖ and ‖ Wˆi(k2)‖ converge by DCL.

Fig. 5. NN weights ‖ Wˆi(k1)‖ and ‖ Wˆi(k2)‖ converge by DDL.

Remark 8:Generally, the convergence speed of NN weights depends on two aspects, 1) the NN weight updating law and 2)the properties of the constructed RBF NN. Firstly, some other weight updating laws, such as projection type, least-squares type, composite type, can be considered to speed up the convergence of NN weights in future research. Secondly, it has been shown in [49] that, for RBF NN, the larger persistent excitation (PE) level (the larger α0in (8)) can achieve the faster convergence speed of NN weights. As we know, the improvement of the PE level is a challenging topic, which will be our future research direction.

B. Simulation Results on Experiences Based Learning Control

In this part, we further show the learning control performance using the experience obtained from the stable adaptive NN control process. The constant NN weights are acquired from a stable time segment as

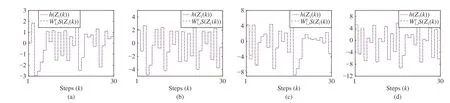
Fig. 6. Function approximation using NN weights learned by DCL under different trajectories: (a) p1=0.3; (b) p1=0.5; (c) p1=0.9 ; and (d) p1=1.1.

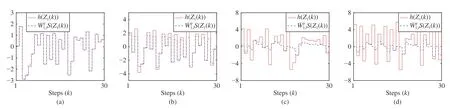
Fig. 7. Function approximation using NN weights learned by DDL under different trajectories: (a) p1=0.3 ; (b) p1=0.5; (c) p1=0.9 ; and (d) p1=1.1.

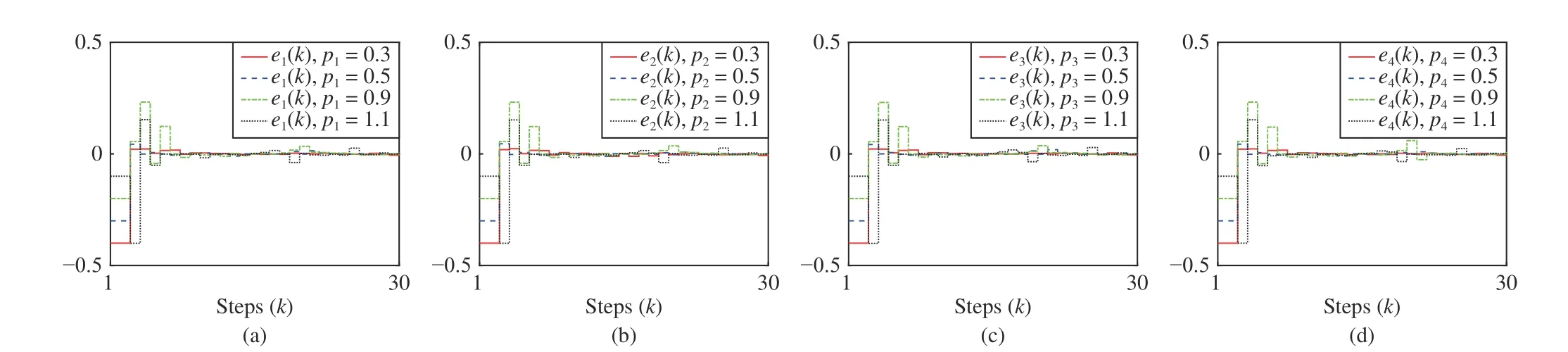
Fig. 8. Tracking errors e i(k) under different reference trajectories by DCL: (a) agent 1; (b) agent 2; (c) agent 3; and (d) agent 4.

Fig. 9. Tracking errors e i(k) under different reference trajectories by DDL: (a) agent 1; (b) agent 2; (c) agent 3; and (d) agent 4.

Fig. 10. Tracking errors e i(k) by ANC (27) and LC (49): (a) agent 1; (b) agent 2; (c) agent 3; and (d) agent 4.

TABLE I COMPARISONS BETWEEN ANC AND LC OF AGENT 1

VI. CONCLUSIONS

This paper has considered DCL problem for a class of discrete-time multi-agent systems under strongly connected and balanced directed graphs. The difficulty of estimated NN weight convergence over directed graphs has been solved by developing an stability result for a class of nonsymmetric LTV systems. Subsequently, a new exponential convergence lemma has been developed for a class of LTV systems with time delays. Such a lemma has been combined with the properties of matrix null-space to show that the estimated NN weights of all agents can exponentially converge to small neighbourhoods of their common optimal values. Based on the convergent NN weights, the experience-based learning control scheme has been presented to demonstrate the NN learning generalization ability and achieve the improved control performance for the same or similar control tasks. Based on the proposed DCL method, there are several meaningful directions for future research, including i) the consideration of other communication topologies, such as strongly connected directed graphs and time-varying graphs; ii) the convergence speed of NN weights; iii) other practical engineering application.