Integrating Conjugate Gradients Into Evolutionary Algorithms for Large-Scale Continuous Multi-Objective Optimization
Ye Tian, Haowen Chen, Haiping Ma, Xingyi Zhang,,Kay Chen Tan,, and Yaochu Jin,
Abstract—Large-scale multi-objective optimization problems(LSMOPs) pose challenges to existing optimizers since a set of well-converged and diverse solutions should be found in huge search spaces. While evolutionary algorithms are good at solving small-scale multi-objective optimization problems, they are criticized for low efficiency in converging to the optimums of LSMOPs. By contrast, mathematical programming methods offer fast convergence speed on large-scale single-objective optimization problems, but they have difficulties in finding diverse solutions for LSMOPs. Currently, how to integrate evolutionary algorithms with mathematical programming methods to solve LSMOPs remains unexplored. In this paper, a hybrid algorithm is tailored for LSMOPs by coupling differential evolution and a conjugate gradient method. On the one hand, conjugate gradients and differential evolution are used to update different decision variables of a set of solutions, where the former drives the solutions to quickly converge towards the Pareto front and the latter promotes the diversity of the solutions to cover the whole Pareto front. On the other hand, objective decomposition strategy of evolutionary multi-objective optimization is used to differentiate the conjugate gradients of solutions, and the line search strategy of mathematical programming is used to ensure the higher quality of each offspring than its parent. In comparison with state-of-the-art evolutionary algorithms, mathematical programming methods, and hybrid algorithms, the proposed algorithm exhibits better convergence and diversity performance on a variety of benchmark and real-world LSMOPs.
I. INTRODUCTION
MANY optimization problems in scientific research and engineering applications have multiple objectives and a large number of decision variables, which are known as largescale multi-objective optimization problems (LSMOPs) [1].For example, time-varying ratio error estimation aims to find true phase voltages by optimizing two objectives and four constraints [2], and fluence map optimization aims to find the optimal beam weights for intensity-modulated radiotherapy by optimizing several objectives [3], [4]. Such LSMOPs contain hundreds or thousands of decision variables, making them challenging to be solved by conventional optimizers. The difficulties mainly lie in the need for a set of well-converged and diverse solutions rather than a single one, preventing conventional optimizers from striking a balance between convergence and diversity [5].
More recently, a number of multi-objective evolutionary algorithms (MOEAs) have been tailored for solving LSMOPs,which tackle the huge search spaces by decision variable grouping, search space reduction, or novel search strategies[6]. The decision variable grouping based MOEAs divide the large number of decision variables into multiple groups and alternately optimize each group of variables, hence the optimal solutions can be approximated in a divide-and-conquer manner [1]. The search space reduction based MOEAs directly reduce the number of decision variables, which is achieved by problem transformation or dimensionality reduction strategies [7], [8]. The novel search strategy based MOEAs generate well-converged solutions by suggesting new search strategies, including variation operators and probability models [9], [10]. These MOEAs can obtain a set of diverse solutions in a single run, but the approximation of global optimal solutions still requires a large number of function evaluations, though they are much faster than conventional MOEAs.
Mathematical programming methods, on the other hand, can quickly converge to a single optimum with the assistance of function information. For solving nonlinear and unconstrained optimization problems, the first-order methods (e.g.,steepest descent [11] and Adam [12]) and the second-order methods (e.g., Newton’s method [13] and the BFGS method[14]) can be adopted. Moreover, there exist a variety of methods tailored for specific types of problems, such as the simplex method for linear programming [15], the Lagrange multiplier method for quadratic programming [16], the Levenberg-Marquardt algorithm for least squares problems [17], the sequential quadratic programming for constrained optimization [18], and the operator splitting method for conic optimization [19]. However, most mathematical programming methods can only generate a single solution at a time, and are inefficient in generating a set of diverse solutions. More seriously, they have difficulties in handling nonconvex problems,which refers to two different cases as illustrated in Fig. 1. On the one hand, for problems with nonconvex landscapes, these methods are vulnerable to getting trapped in local optimums due to the use of gradients [20]. On the other hand, for problems with nonconvex Pareto fronts, these methods can only find extreme solutions, which always have the minimum objective values regardless of the weight vector for the aggregation of multiple objectives [21].
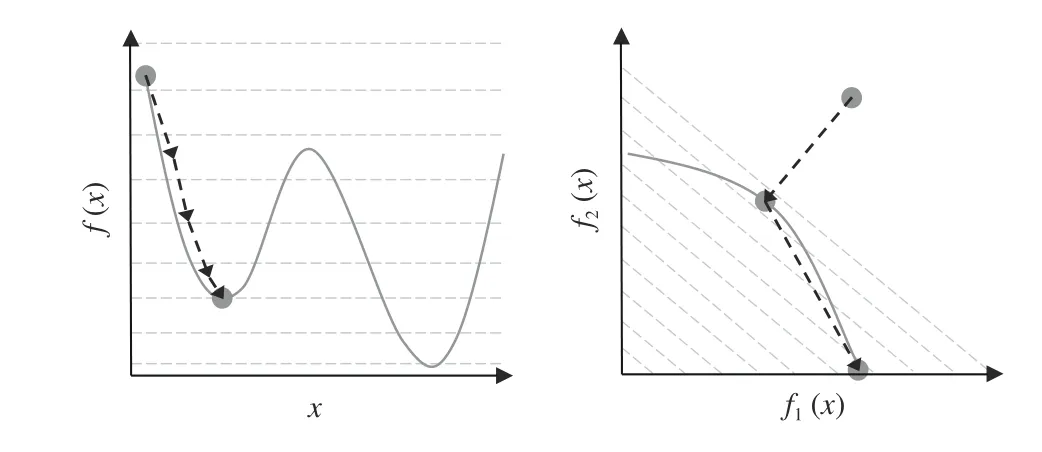
Fig. 1. A problem with nonconvex landscape (left) and a problem with nonconvex Pareto front (right).
As a consequence, evolutionary computation and mathematical programming are developed by two huge but almost completely disjoint communities, each with its own strengths and weaknesses [22]. MOEAs are suitable for solving smallscale multi-objective optimization problems owing to the population based evolutionary framework, while mathematical programming methods are effective for solving large-scale single-objective optimization problems with the assistance of gradients. By contrast, MOEAs exhibit slow convergence speed on large-scale optimization problems since they search in a black-box manner, and mathematical programming methods have poor diversity on multi-objective optimization problems due to the single-point search paradigm. Thus, the integration of MOEAs and mathematical programming methods turns out to be a key issue in solving continuous LSMOPs.However, little attention has been paid to this direction and existing hybrid algorithms just attach gradient based local search to MOEAs [23], [24], whereas the deep integration of the two types of optimizers is rare. To bridge the gap between evolutionary computation and mathematical programming for better solving LSMOPs, this work proposes a new algorithm by combining multi-objective differential evolution and a conjugate gradient method, which is expected to drive a set of solutions to quickly converge towards different regions of the Pareto front. This paper contains the following contributions:
1) Based on a review of existing MOEAs, mathematical programming methods, and hybrid algorithms, this paper analyzes their limitations in solving LSMOPs. Also, an important but overlooked issue is discussed, i.e., how to obtain the gradients of continuous LSMOPs.
2) To better solve LSMOPs, this paper proposes a hybrid method for generating solutions. Firstly, it generates solutions based on conjugate gradients to quickly approximate the Pareto optimal solutions. Secondly, it uses differential evolution to tune the solutions to enhance population diversity.Thirdly, it adopts the objective decomposition strategy used in MOEAs to assist the conjugate gradient based search, and adopts the line search strategy used in mathematical programming to assist differential evolution. By inheriting the good convergence performance of conjugate gradient methods and the good diversity performance of differential evolution, the population is expected to have good convergence and diversity at last.
3) Moreover, this paper proposes a multi-objective conjugate gradient and differential evolution (MOCGDE) algorithm. The proposed algorithm evolves a small population using the proposed hybrid method, and maintains a large archive to collect a set of well-converged and diverse solutions as the output. According to the experimental results on three benchmark suites and two real-world applications with up to 10 000 decision variables, the proposed algorithm shows significantly better convergence and diversity performance than 11 state-of-the-art MOEAs, mathematical programming methods, and hybrid algorithms.
The remainder of this paper is structured as follows. Section II reviews existing work and discusses one relevant issue,Section III details the procedure of the proposed algorithm,Section IV analyzes the experimental results, and Section V concludes this paper.
II. BACKGROUND AND RELATED WORK
This work focuses on continuous optimization problems with or without constraints, which can be mathematically defined as

A. Evolutionary Algorithms for Solving LSMOPs
Although conventional MOEAs can tackle multiple objectives by using dominance based [25], decomposition based[21], or indicator based [26] selection strategies, they are inefficient in finding well-converged solutions in the huge search spaces of LSMOPs. To address this dilemma, three categories of MOEAs have been developed, but they still encounter difficulties in balancing between efficiency and effectiveness.
The first category of MOEAs divides the decision variables into multiple groups via different strategies, which mainly include random grouping, differential grouping, and variable analysis. The random grouping is very efficient since it randomly divides the decision variables into a predefined number of groups with equal size [1], but it may drive the solutions towards local optimums since the interactions between variables are totally ignored. The differential grouping is more effective for approximating global optimal solutions due to the detection of interactions between variables [27], but it holds quite a high computational complexity since the interaction between each two variables should be detected independently.The variable analysis serves as a supplement of differential grouping [28], which can distinguish between the variables contributing to convergence and diversity but is still time-consuming.
The second category reduces the number of decision variables via problem transformation or dimensionality reduction strategies. Instead of optimizing the decision variables,the problem transformation strategies explore the huge search space by optimizing a weight vector acting on existing solutions, and the number of optimized variables can be highly reduced since the weight vector is much shorter than decision vectors [7], [29]. But this is at the expense of effectiveness,where local optimal solutions can be efficiently found while global optimal solutions are likely to lose in the weight vector space [30]. By contrast, the dimensionality reduction strategies aim to reduce the search space via machine learning [31],data mining [32], or other techniques [33], which consider variable interactions and can retain the global optimal solutions in the reduced search space. However, the dimensionality reduction strategies are only suitable for specific LSMOPs like those with low intrinsic dimensions [31] or sparse optimal solutions [24].
The third category customizes new variation operators or probability models to efficiently approximate the global optimal solutions in the original search space. The customized variation operators are enhancement of existing ones such as genetic operators [34], competitive swarm optimizer [35], and covariance matrix adaptation evolution strategy [36]. The customized probability models generate new solutions by characterizing promising solutions found so far, which is achieved by Gaussian process [10], generative adversarial networks[37], mirror partition based solving knowledge [38], and other techniques [39]. These search strategies can improve the convergence speed of existing MOEAs on LSMOPs, but a large number of function evaluations are still required to reach the global Pareto front.
B. Mathematical Programming Methods for Nonlinear and Unconstrained Optimization
On the contrary, mathematical programming methods converge much faster since the search direction is guided by gradients. In terms of nonlinear and unconstrained optimization,mathematical programming methods can be divided into three categories. The first category updates solutions according to first-order gradients, such as steepest descent [11] and many momentum assisted methods like Nesterov’s method [40],RMSProp [41], and Adam [12]. These methods have very low computational complexities, which are efficient for solving problems with many decision variables, e.g., the training of deep neural networks [20]. The second category updates solutions according to second-order gradients, such as Newton’s method [13], the quasi-Newton method [42], and the BFGS method [14]. These methods have much faster convergence speeds than the first-order methods, but they are efficient for only small-scale problems since the calculation of the inverse of the Hessian matrix or its approximation is extremely timeconsuming. The third category refers to conjugate gradient methods [43], which update solutions according to the linear combination of the current and historical gradients. The conjugate gradient methods only need to calculate the first-order gradients, and its convergence speed is between those of the first- and second-order methods, holding a good balance between efficiency and effectiveness for solving large-scale problems. Therefore, this work adopts a popular conjugate gradient method in the proposed algorithm, namely, the FRCG(Fletcher-Beeves conjugate gradient) method [44].
Nevertheless, the above mathematical programming methods are customized for single-objective optimization, where a single gradient has to be obtained to update each solution. To handle multi-objective optimization problems, the weighted sum method aggregates multiple objectives by a predefined weight vector [45], Wierzbicki’s method aggregates multiple objectives by a predefined reference point [46], and theϵ-constraint method optimizes a single objective and regards the others as constraints [47]. To eliminate the requirement of decision makers’ preferences, the multi-objective steepest descent method [48], [49] and multi-objective Newton’s method [50] were suggested, which can converge to a solution that satisfies certain first-order necessary conditions of Pareto optimality without the aggregation of multiple objectives. While the above methods can only generate one solution at a time, a gradient based multi-objective optimization method incorporates a population based aggregative strategy[51], and is further enhanced with a distance constraint technique to handle nonconvex Pareto fronts [52]. However, the obtained populations have poor diversity since the method does not adopt effective diversity preservation strategies.
C. Evolutionary Algorithms Assisted by Gradients
To obtain a set of diverse solutions in a single run, some hybrid algorithms have been suggested to integrate evolutionary algorithms with gradient based local search strategies.These hybrid algorithms can be grouped into two categories,according to whether the true gradients or pseudo-gradients are used. The first category generates solutions by variation operators and true gradients, for instance, the Gaussian mutation and RProp work cooperatively to generate solutions in[23], the solutions obtained by particle swarm optimization are updated by the quasi Newton-Raphson algorithm in [53],and the solutions generated by a sparse multi-objective evolutionary algorithm are tuned by stochastic gradient descent in[24]. To inherit both the exploration ability of genetic operators and the exploitation ability of gradient descent for deep neural network training, a gradient based simulated binary crossover operator is developed in [20], where the population can escape from local optimums and quickly converge to the global Pareto front. The second category generates solutions by variation operators and pseudo-gradients, for example, a gradient based local search is attached to the genetic algorithm in [54] and the gradient information is involved in the variation operator of particle swarm optimization in [55], both of which estimates the gradients by using finite difference. In[56], the evolutionary gradient search estimates the gradient through random mutations on the current solution, and this method is further extended to multi-objective optimization in[57].
In spite of the assistance of gradient information, the hybrid algorithms for multi-objective optimization have not yet received much attention in the community, which is mainly due to the following two reasons. Firstly, the variation operators are simply tailed by gradient based local search in existing work, which accelerates the convergence speed but is harmful to the diversity preservation in objective spaces. Secondly, most existing work focuses on optimizing a single objective, while the aggregation of the gradients of multiple objectives is rarely touched. As a consequence, the performance of evolutionary algorithms can be enhanced on largescale single-objective optimization problems, but such problems have already been solved by mathematical programming methods. By contrast, mathematical programming methods are ineffective for LSMOPs, which also pose challenges to existing hybrid algorithms.
Therefore, this work proposes an effective hybrid algorithm for solving LMOPs by deeply integrating evolutionary computation with mathematical programming. Before the description of the proposed algorithm, the way to calculate the gradients of continuous LSMOPs is discussed in the following.
D. Calculation of Gradients
To use mathematical programming methods for solving LSMOPs, the first issue is to calculate the gradients of given solutions. For the continuous objective functions whose first partial derivatives are available, the Jacobian matrix can be directly calculated by
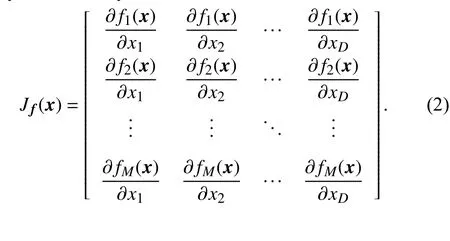

To consider both black- and white-box scenarios in the experiments, we regard the benchmark LSMOPs as black-box problems and approximate the Jacobian matrix by (4), and regard the real-world LSMOPs as white-box problems and calculate the Jacobian matrix by hand. In short, the proposed algorithm is a metaheuristic since it can solve black-box problems by approximating the gradients, and is also a heuristic since it can solve white-box problems by using the partial derivatives directly. By contrast, the proposed algorithm is different from matheuristics [59], since the proposed algorithm is a problem-independent method based on mathematical programming methods and metaheuristics for continuous optimization, while matheuristics are problem-dependent methods mostly based on mathematical programming models and ad hoc heuristics for combinatorial optimization.
III. THE PROPOSED ALGORITHM
A. Procedure of the Proposed MOCGDE
The general procedure of the proposed multi-objective conjugate gradient and differential evolution (MOCGDE) algorithm is illustrated in Fig. 2. As can be observed, the proposed algorithm maintains two solution sets during the optimization process, including a populationPevolved by conjugate gradients and differential evolution, and an archiveAstoring the feasible and non-dominated solutions found so far.The population has a small size to save computational resources, since each solution in the population is updated by conjugate gradients and differential evolution independently.By contrast, the archive has a large size to store sufficient promising solutions as the output, and also provide alternatives to replace prematurely converged solutions in the population.
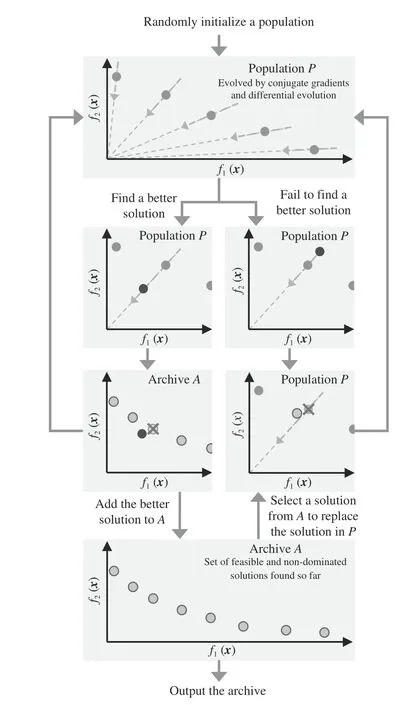
Fig. 2. General procedure of the proposed MOCGDE.

Algorithm 1: Procedure of MOCGDE Input: D (number of decision variables), (size of population),(size of archive)Output: A (final archive)P ← NP NP NA 1 Generate random solutions;W ← NP 2 Generate uniformly distributed weight vectors;A ←UpdateArchive(P,NA)3 ;K ←1×D 4 vector of zeros; //Counters for restart G ←Ø 5 ; //Set of gradients S ←Ø 6 ; //Set of search directions 7 while termination criterion is not fulfilled do i=1,...,|P|8 for do[g,di f f]←CalGradient(P[i],W[i])9 ;mod(K[i],D)==0 10 if then s ←-g 11 ;12 else s ←-g+ ggT 13 ;K[i]←K[i]+1 G[i]G[i]T S[i]14 ;G[i]←g 15 ;S[i]←s 16 ;[x,success]←GenS olution(P[i],A,s,di f f)17 ;success 18 if then P[i]←x 19 ;A ←UpdateArchive(A∪{x},NA)20 ;21 else P[i]←22 Randomly select a solution from A;K[i]←0 23 ;24 return A.
As described in Algorithm 1, the proposed algorithm starts with the random generation of a populationP(Line 1), then the same number of uniformly distributed weight vectors are generated by Das and Dennis’s method [60] to differentiate the convergence directions of the solutions inP(Line 2). Of course, the weight vectors can also be generated by other sampling methods such as the Taguchi method [61] and uniform design [60]. Besides, an archiveAand the other variables are also initialized (Lines 3–6). In each iteration, each solution in the population is updated by conjugate gradients and differential evolution in turn, and the newly generated solution is used to update the population and the archive. More specifically,the gradient of a solution is first calculated (Line 9), and the next search directionsis calculated (Lines 10–13) according to the following formula suggested in FRCG [44]:

Afterwards, the obtained search direction together with differential evolution is used to update the solution (Line 17). If a better solution is found, the solution is used to replace its ancestor in the population (Line 19) and update the archive(Line 20). While if no better solution is found, a solution randomly selected from the archive is used to replace the ancestor in the population (Line 22) and restart the conjugate gradient iterations (Line 23). The procedure of updating the archive is detailed in Algorithm 2, where all the dominated solutions are first removed from the archive (Line 1), and then the solution with the shortest Euclidean distance to the others is removed one by one (Lines 3–9), until the archive does not exceed its maximum size (Line 2).

Algorithm 2:UpdateArchive(A,NA)Input: A (archive), (size of archive)Output: A (updated archive)A ←NA 1 Remove the dominated solutions from A;|A|>NA 2 while do[x,y]← x,y∈A, x≠y‖f(x)-f(y)‖3 argmin ;disx ← z∈A{x,y}‖f(x)-f(z)‖4 min ;disy ← z∈A{x,y}‖f(y)-f(z)‖5 min ;disx <disy 6 if then A ←A{x}7 ;8 else A ←A{y}9 ;10 return A.
In the next subsections, the two core components of the proposed algorithm are elaborated, including the calculation of gradients and the generation of solutions.
B. Calculating Gradients in the Proposed MOCGDE
Algorithm 3 presents the procedure of calculating gradients in the proposed MOCGDE. Since the algorithm is tailored for both unconstrained and constrained optimization, the Jacobian matrix of the constraints is calculated if the current solution is infeasible (i.e., at least one constraint function value is larger than zero) (Line 2), and the Jacobian matrix of the objectives is calculated if the current solution is feasible (Line 7). The Jacobian matrix can be calculated directly if the partial derivatives are available, and has to be estimated by finite difference if the partial derivatives are unavailable.

Algorithm 3:CalGradient(x,w)Input: x (current solution), w (weight vector)Output: g (gradient), diff (variables with different signs of partial derivatives on all objectives)∃i ∈{1,...,p}:hi(x)>0 1 if then Jh(x)←2 Calculate the Jacobian matrix of constraints directly or by finite difference;w ←1×|w|3 vector of ones;g ←wJh(x)4 ;di f f ←Ø 5 ;6 else Jf(x)←7 Calculate the Jacobian matrix of objectives directly or by finite difference;g ←wJf(x)8 ;di f f ←Jf(x)9 Set of variables with different signs of partial deriva tives in ;10 return .g,di f f
It is worth noting that the weight vectors for aggregating the constraints and the objectives are different. Since all the constraints must be satisfied, the weight vector for aggregating the constraints is set to a vector of ones (Lines 3 and 4), which equates the weights of all the constraints. By contrast, since the solutions should make diverse trade-offs between the objectives, the weight vector for aggregating the objectives is predefined (Line 8), where each solution is associated with a distinct weight vector as well as convergence direction. In short, the use of gradients aims to enhance population convergence, while the uniformly distributed weight vectors are responsible for preserving population diversity. Besides, since the first partial derivatives of a decision variable may have different signs on all the objectives, which means that the update of this decision variable will decrease some objectives but increase the others, such decision variables are stored in the variablediff(Line 9) and will not be updated to ensure the solution can converge along the predefined direction.
C. Generating Solutions in the Proposed MOCGDE
Algorithm 4 presents the procedure of generating solutions in the proposed MOCGDE. To determine a suitable step size,a simple line search strategy is used to exponentially reduce the step sizemfrom 1 until a better solution is found. To be specific, a new solutionyis obtained by updating an existing solutionxaccording to the following formula:


Algorithm 4:GenS olution(x,A,s,di f f)Input: x (current solution), A (archive), s (search direction), diff(variables with different signs of partial derivatives on all objectives)success Output: y (new solution), (whether a better solution is found)success ←1 false;m=0,...,9 2 for do y ←1×|x|3 vector of zeros;[x′,x′′]←4 Randomly select two solutions from A;5 for do i ∉dif f i=1,...,|x|6 if then yi ←xi+0.5m×si 7 ;8 else yi ←xi+0.5m×(x′i-x′′i )9 ;CVx ←∑p i=1 max{hi(x),0}10 ;CVy ←∑p i=1 max{hi(y),0}11 ;CVy <CVx||CVy==CVx&&f(y)≺f(x)12 if then success ←13 true;14 break;y,success 15 return .
After a new solution is obtained, the line search terminates if the new solution is better than the original one (Lines 12–14). Formally, solutionyis better than solutionxifyhas a smaller constraint violation thanx
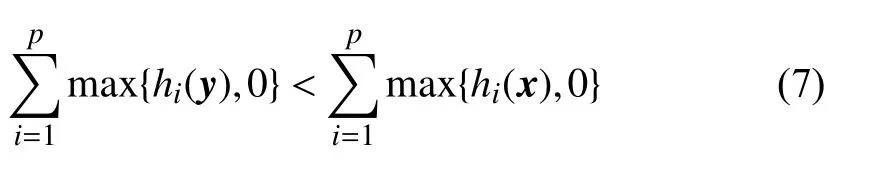
or they have the same constraint violation andydominatesx
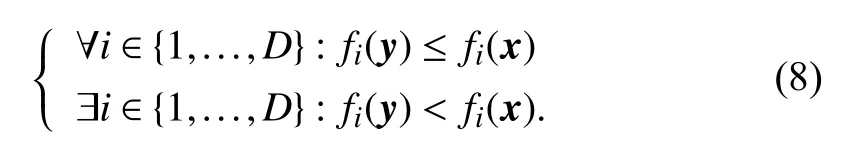
D. Computational Complexity of the Proposed MOCGDE

E. Discussions
To summarize, the proposed MOCGDE suggests a deep combination of mathematical programming and evolutionary computation. More specifically, the conjugate gradient method and differential evolution are used to update solutions collaboratively, the uniform weight vectors suggested in decomposition based MOEAs are used to differentiate the search directions used in the conjugate gradient method, and the line search strategy suggested in mathematical programming is used to ensure that the population evolved by evolutionary algorithms can always generate better offspring. In comparison with existing hybrid algorithms, the proposed algorithm has the following advantages:
1)Framework:Most existing algorithms evolve a single population, where a small population cannot generate many diverse solutions and a large population wastes many computational resources. By contrast, the proposed algorithm drives a small population towards the global optimums, and maintains a large archive to store sufficient diverse solutions.
2)Gradients:Most existing algorithms consider the gradients of a single objective, which do not explicitly define weight vectors to aggregate multiple objectives and differentiate the search directions of multiple solutions. By contrast, the proposed algorithm uses an objective decomposition strategy to associate each solution with a distinct weight vector, and thus the solutions can spread along the whole Pareto front. In addition, the proposed algorithm also considers the gradients of constraints when needed, which is suitable for both unconstrained and constrained optimization.
3)Operators:Most existing algorithms directly attach gradient based local search to the variation operators of evolutionary algorithms, where the population diversity may deteriorate due to the difference between the signs of first partial derivatives on all the objectives. By contrast, the proposed algorithm only uses conjugate gradients to update the decision variables having the same sign of first partial derivatives on all the objectives, and thus each solution can converge along its predefined direction. Moreover, the proposed algorithm uses differential evolution to tune the remaining decision variables, which can further enhance population diversity.
As a consequence, the proposed MOCGDE inherits both the fast convergence speed of mathematical programming methods and the good diversity performance of evolutionary algorithms, and is also very efficient since it holds the same computational complexity as conjugate gradient methods and differential evolution. In the next section, the performance of the proposed MOCGDE is verified by comparing it with state-ofthe-art algorithms on benchmark and real-world LSMOPs.
IV. ExPERIMENTAL STUDIES
A. Comparative Algorithms
Eleven representative algorithms are involved in the experiments, including three MOEAs, three mathematical programming methods, and five hybrid algorithms. The three MOEAs are NSGA-II (non-dominated sorting genetic algorithm II)[25], LSMOF (large-scale multi-objective optimization framework) [29], and LMOCSO (large-scale multi-objective competitive swarm optimizer) [9], where NSGA-II is one of the most classical multi-objective evolutionary algorithms, LSMOF is a problem transformation based large-scale MOEA, and LMOCSO is a new variation operator based large-scale MOEA. The three mathematical programming methods include FRCG [44], Izui’s algorithm [51], and MOSD (multiobjective steepest descent) [49], where FRCG is a popular conjugate gradient method, Izui’s algorithm is a population based multi-objective linear programming method, and MOSD is a multi-objective steepest descent algorithm. The five hybrid algorithms are NSGA-II + gradient, NSGA-II +gSBX (gradient based simulated binary crossover) [20], MOEGS (multi-objective evolutionary gradient search) [57],GPSO (gradient based particle swarm optimization) [53], and SAPSO (semi-autonomous particle swarm optimizer) [55],where NSGA-II + gradient denotes that each solution generated by NSGA-II is tuned by a line search based steepest descent, NSGA-II + gSBX denotes the NSGA-II with gradient based simulated binary crossover, MO-EGS is a multiobjective evolutionary gradient search algorithm, GPSO is a combination of particle swarm optimization and the quasi Newton-Raphson algorithm, and SAPSO integrates gradient information into the variation operator of particle swarm optimization.
Table I lists the detailed settings of all the compared algorithms, which mostly follow those suggested in their original papers. Since the calculations of objectives and Jacobian matrices are with different computational complexities, the CPU time rather than the number of function evaluations is adopted as the termination criterion for fairness. It should be noted that FRCG, MOSD, MO-EGS, GPSO, and SAPSO can only generate a single solution at a time, hence they are executed many times with the assistance of a set of uniformly distributed weight vectors [60] for the aggregation of multiple objectives, and the total CPU time is also divided into the same number of stages. Since most of the compared algorithms are not tailored for constrained optimization, these algorithms use the same constraint handling strategies as theproposed MOCGDE, i.e., the constraints are given higher priority than the objectives when calculating gradients and comparing solutions.

TABLE I DETAILED SETTINGS OF THE COMPARED ALGORITHMS
B. Test Problems
Three multi-objective test suites are adopted to test the performance of the compared algorithms, including ZDT (Zitzler-Deb-Thiele problems) [65], DTLZ (Deb-Thiele-Laumanns-Zitzler problems) [66], and IMF (inverse modeling functions)[10], which contain 22 scalable benchmark problems in total.These problems contain two or three objectives without constraint, and the number of decision variables is set to 1000 and 10 000. Two real-world problems are also adopted, including time-varying ratio error estimation (TREE) [2] and fluence map optimization (FMO) [3], [4]. The TREE problems contain two objectives with three or four constraints, aiming to minimize the total ratio error and ratio error variation and satisfy the constraints of topology, series, and phase. The FMO problems are very important in intensity-modulated radiotherapy [3], which contain two objectives without constraint and aim to satisfy the requirements of maximum and minimum doses. The number of decision variables of the real-world problems varies from 1000 to 9900, depending on the five datasets involved in the TREE problems and the three datasets involved in the FMO problems.
In terms of mathematical programming methods, the Jacobian matrix is approximated by finite difference on each benchmark problem and calculated directly on each real-world problem. The inverted generational distance (IGD) [67] and hypervolume (HV) [68] are adopted as the performance indicators. For the populations obtained on benchmark problems,approximately 10 000 reference points are sampled by the methods suggested in [60] for IGD calculation. For the populations obtained on real-world problems, the solutions in all the populations for the same test instance are collected, and a reference point is set to the maximum objective values of the solutions on all dimensions for HV calculation. The experiments are performed for 30 independent runs, and the mean and standard deviation of the indicator values are reported.Moreover, the Friedman test with Bonferroni correction at a significance level of 0.05 is used for statistical test, where “ + ”,“ - ”, and “ ≈ ” mean that the performance of an algorithm is statistically better, worse, and similar to the proposed MOCGDE, respectively. All the experiments are conducted on PlatEMO [69].
C. Comparisons on Benchmark Problems
Table II presents the IGD values obtained by the compared algorithms on ZDT and DTLZ test suites. Generally, the proposed MOCGDE gains the best results on 18 out of 24 test instances, which is followed by LSMOF gaining the best results on the remaining 6 test instances. Therefore, for general continuous LSMOPs, the proposed MOCGDE shows superiority over existing optimizers based on evolutionary computation or/and mathematical programming. Furthermore,for the IMF problems with complex linkages between variables, MOCGDE also exhibits better performance than existing algorithms, which obtains the best results on 13 out of 20 test instances as shown in Table III.
Fig. 3 depicts the populations with median IGD values obtained by the compared algorithms on 1000-variable ZDT1.For the three evolutionary algorithms NSGA-II, LSMOF, and LMOCSO, only LSMOF can reach the Pareto front since ithas a fast convergence speed due to the problem transformation strategy. For the three mathematical programming methods FRCG, Izui’s algorithm, and MOSD, only FRCG can find a few optimal solutions since it is much more efficient than the first-order methods used in Izui’s algorithm and MOSD.Nevertheless, FRCG exhibits poor diversity performance since it is not tailored for multi-objective optimization. For the five hybrid algorithms NSGAII-II + gradient, NSGA-II + gSBX,MO-EGS, GPSO, and SAPSO, only GPSO can find a few optimal solutions since it adopts the quasi-Newton method to update the solutions. By contrast, NSGA-II + gradient adopts only a first-order method, which has a slow convergence speed; NSGA-II + gSBX and SAPSO integrate the first-order gradient information into the variation operators, where the solutions are not specifically optimized by mathematical programming methods; MO-EGS approximates the first partial derivatives by (3) rather than finite difference, the gradients obtained by which are inaccurate and unable to optimize the solutions effectively. On the other hand, the proposed MOCGDE can obtain a set of solutions uniformly distributed along the whole PF, holding a good balance between convergence and diversity. The superiority of MOCGDE is more significant on 1000-variable IMF1 as shown in Fig. 4, where the problem introduces complex linkages between variables and only MOCGDE can obtain a set of well-converged and diverse solutions.
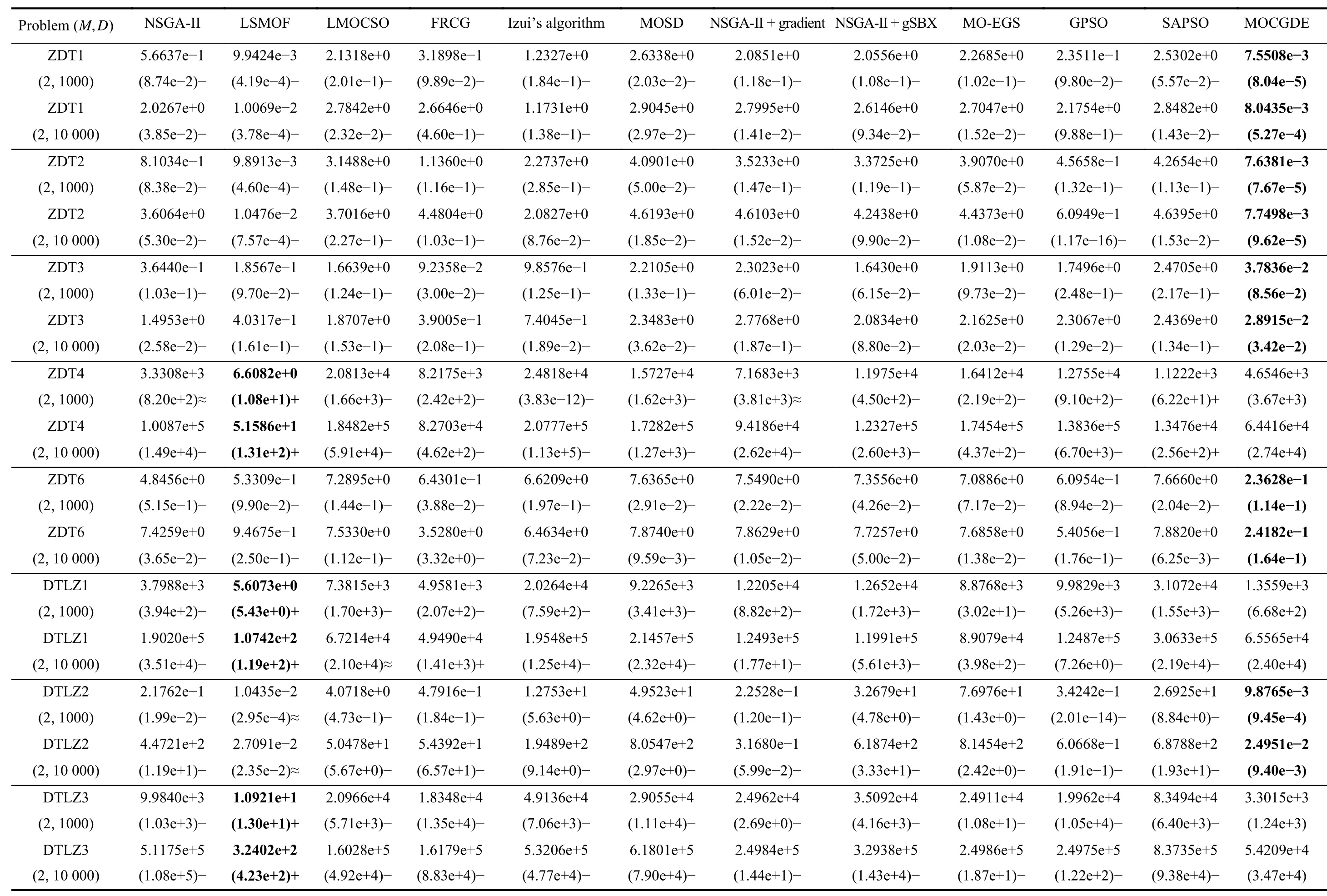
TABLE II IGD VALUES OBTAINED By TWELVE ALGORITHMS ON ZDT AND DTLZ TEST SUITES

IGD VALUES OBTAINED By TWELVE ALGORTITAHBMLSE O INI ZDT AND DTLZ TEST SUITES (CONTINUED)

TABLE III IGD VALUES OBTAINED By TWELVE ALGORITHMS ON IMF TEST SUITE
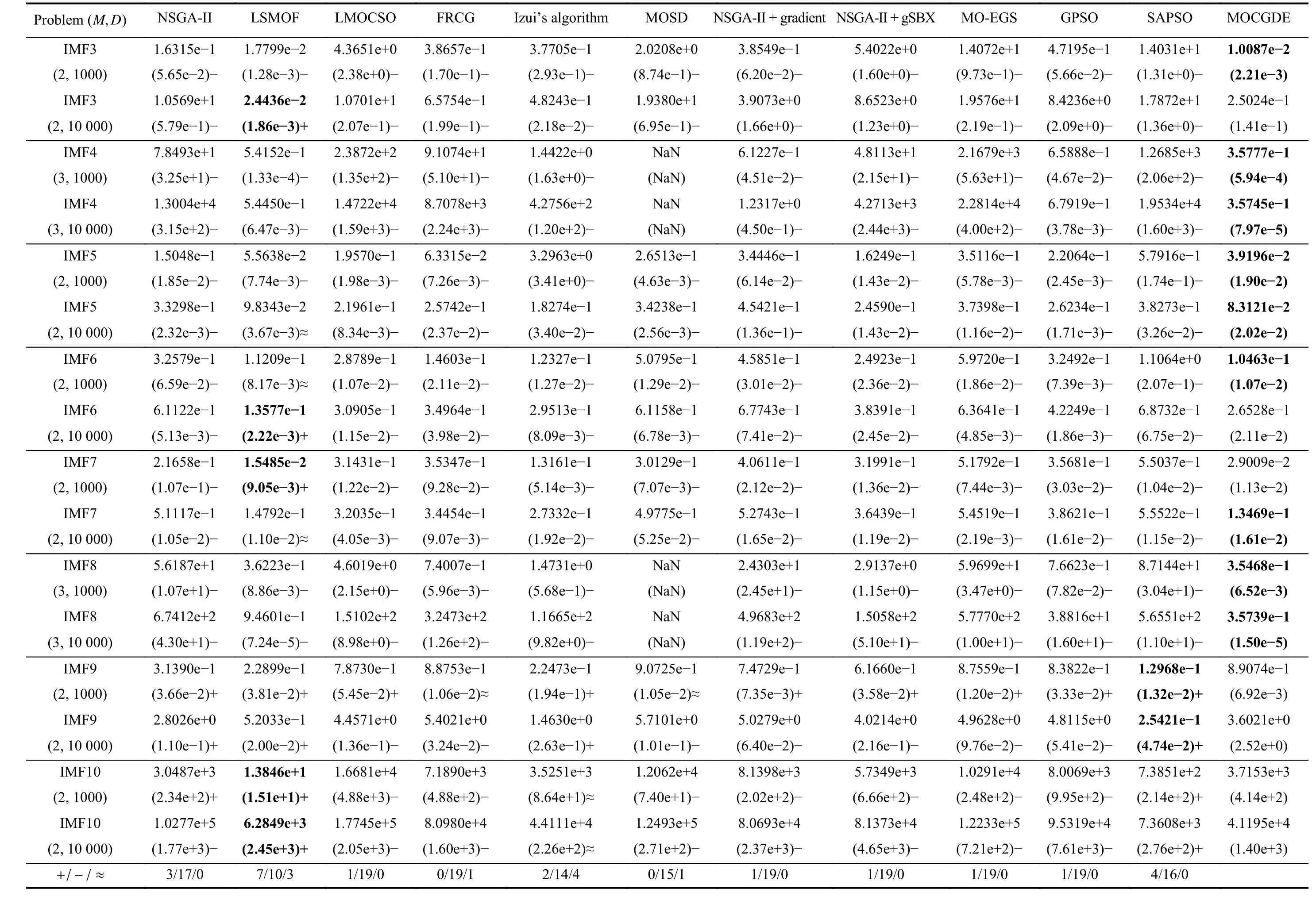
IGD VALUES OBTAINED By TWELVE TAALGBOLREI TIHIIMS ON IMF TEST SUITE (CONTINUED)

Fig. 3. Populations (in objective space) with median IGD values obtained by twelve algorithms on ZDT1 with 1000 decision variables.
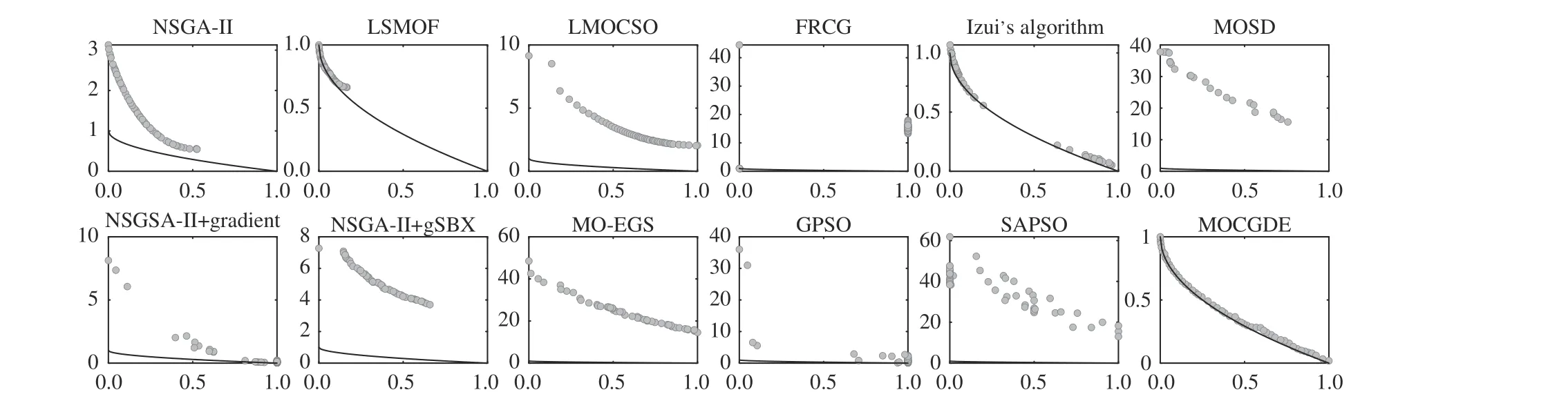
Fig. 4. Populations (in objective space) with median IGD values obtained by twelve algorithms on IMF1 with 1000 decision variables.
Moreover, Fig. 5 plots the IGD values obtained by the compared algorithms on ZDT1 and IMF1 with 1000 to 10 000 decision variables, where the CPU time is proportionally set for different numbers of decision variables. It can be found that the proposed MOCGDE obtains the best IGD values on all the test instances. Besides, the IGD values of MOCGDE fluctuate slightly on ZDT1 and increase steadily on IMF1,since IMF1 contains variable linkages that are very difficult to handle.
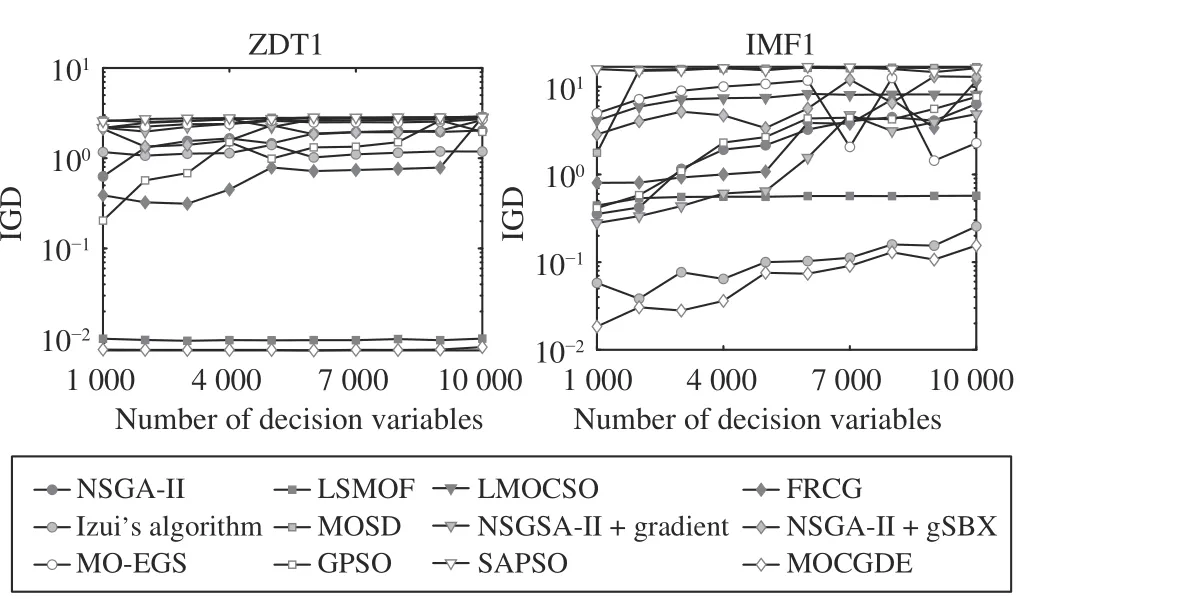
Fig. 5. IGD values obtained by twelve algorithms on ZDT1 and IMF1 with different numbers of decision variables.
The superiority of the proposed MOCGDE over evolutionary algorithms is owing to the assistance of conjugate gradients, which highly improve the convergence speed in huge search spaces. According to the experimental results in Table II,MOCGDE outperforms the evolutionary algorithms NSGA-II,LSMOF, and LMOCSO on all the problems besides ZDT4,DTLZ1, and DTLZ3. In comparison with LSMOF, the inferiority of MOCGDE on ZDT4, DTLZ1, and DTLZ3 is due to their multimodal landscapes, which pose stiff challenges to existing optimizers. For example, aD-variable DTLZ1 problem contains 11D-1-1 local Pareto fronts and one global Pareto front, which is extremely difficult to handle when the number of decision variables is large. In fact, LSMOF is still unable to find the global Pareto fronts of the three problems;instead, it can approximate a local Pareto front quickly.
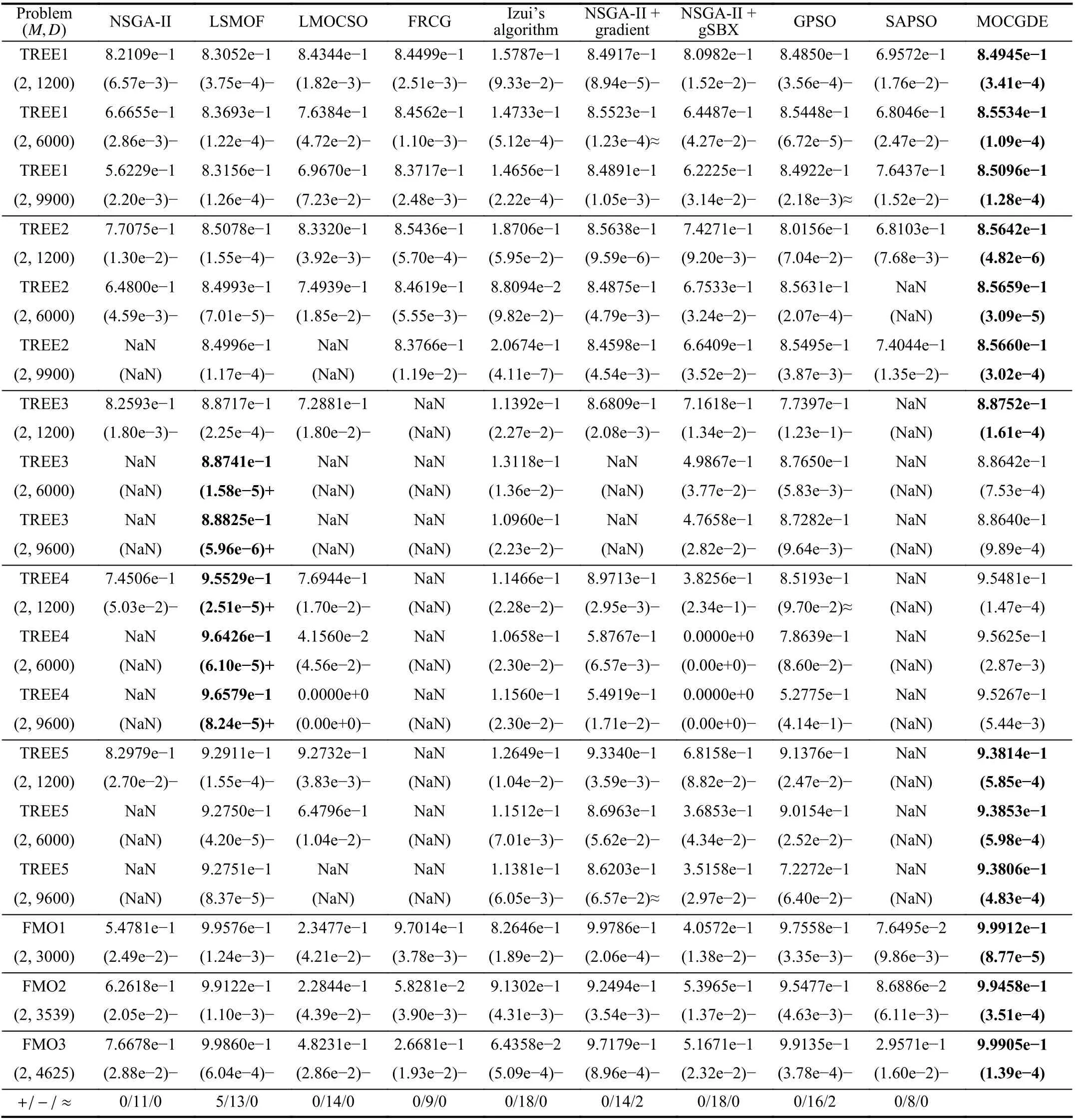
TABLE IV HV VALUES OBTAINED By TEN ALGORITHMS ON THE TREE PROBLEMS AND FMO PROBLEMS
The superiority of the proposed MOCGDE over mathematical programming methods is owing to the evolutionary framework optimizing multiple solutions simultaneously. In particular, the differential evolution enhances the exploration ability of gradient descent and thus reduces the probability of trapping in the local optimums of nonconvex landscapes, and the archive can preserve the population diversity on both convex and nonconvex Pareto fronts. As evidenced by Table II,for ZDT4, DTLZ1, and DTLZ3 with highly multimodal landscapes, MOCGDE significantly outperforms the mathematical programming methods FRCG, Izui’s algorithm, and MOSD. For ZDT1 with a convex Pareto front and ZDT2 with a concave Pareto front, MOCGDE gains very similar IGD values on the two problems, while the IGD values of FRCG,Izui’s algorithm, and MOSD on ZDT2 are much worse than those on ZDT1.
D. Comparisons on Real-World Problems
Table IV lists the HV values obtained by the compared algorithms on the TREE problems and FMO problems. It is noteworthy that the results of MOSD and MO-EGS are not reported since MOSD can only handle two objectives or constraints and MO-EGS cannot obtain any feasible solution for the TREE problems. Besides, some of the results are marked as “NaN” since no feasible solution is obtained. According to the table, the proposed MOCGDE obtains the best HV values on 13 test instances and LSMOF obtains the best HV values on 5 test instances. In terms of statistical tests, the performance of MOCGDE is better than or similar to all the compared algorithms besides LSMOF on all the test instances.Therefore, the effectiveness of MOCGDE on applications is verified.
Fig. 6 plots the populations with median HV values obtained by the compared algorithms on TREE1 with 1200 decision variables. It can be observed that LSMOF obtains a set of solutions with good diversity but poor convergence,GPSO and NSGA-II+gradient obtain multiple solutions with good convergence but poor diversity, and the other compared algorithms can only find a few non-dominated solutions. In particular, despite the uniformly distributed weight vectors adopted in FRCG, only a single non-dominated solution can be found by FRCG. By contrast, the proposed MOCGDE gains a set of well-converged and diverse solutions for TREE1, which is the only algorithm achieving good convergence and diversity performance. Moreover, Fig. 7 plots the populations with median HV values obtained by the compared algorithms on FMO1, where the solutions obtained by MOCGDE are with obviously higher quality than those obtained by the compared algorithms.
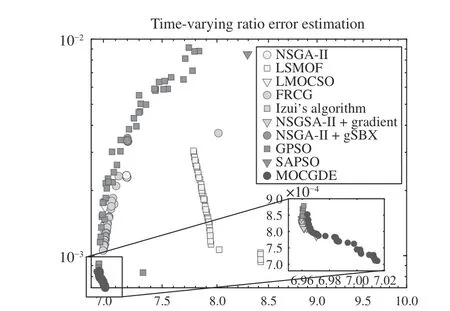
Fig. 6. Populations (in objective space) with median HV values obtained by ten algorithms on TREE1 with 1200 decision variables.
E. Ablation Studies on the Proposed MOCGDE
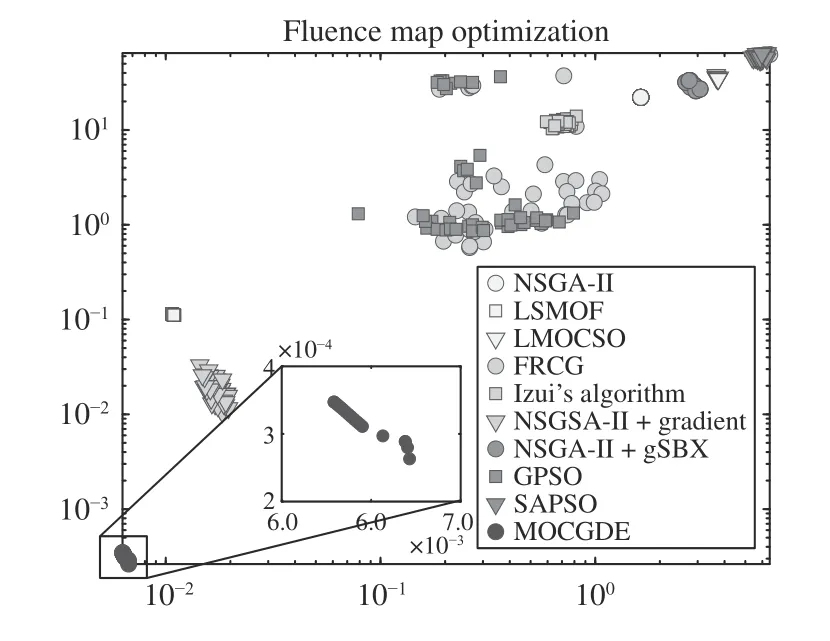
Fig. 7. Populations (in objective space) with median HV values obtained by ten algorithms on FMO1.
To verify the effectiveness of the core component of MOCGDE, i.e., updating solutions by both conjugate gradients and differential evolution, the proposed MOCGDE is compared with four variants on ZDT1 and IMF1, where the first variant uses conjugate gradients to update only the variables out ofdiff, the second variant uses conjugate gradients to update all the variables, the third variant uses differential evolution to update only the variables indiff, and the fourth variant uses differential evolution to update all the variables. It can be found from Fig. 8 that, updating only the variables out ofdiffby conjugate gradients leads to a few well-converged solutions, since the other variables are not updated and the population diversity cannot be ensured. While updating all the variables by conjugate gradients can lead to a set of well-converged and diverse solutions on ZDT1, the solutions obtained on IMF1 have worse convergence and diversity since IMF1 is much more complex. Besides, using only differential evolution cannot obtain any well-converged solution. As a consequence, updating solutions by both conjugate gradients and differential evolution is the most effective way for the proposed MOCGDE to solve LSMOPs.
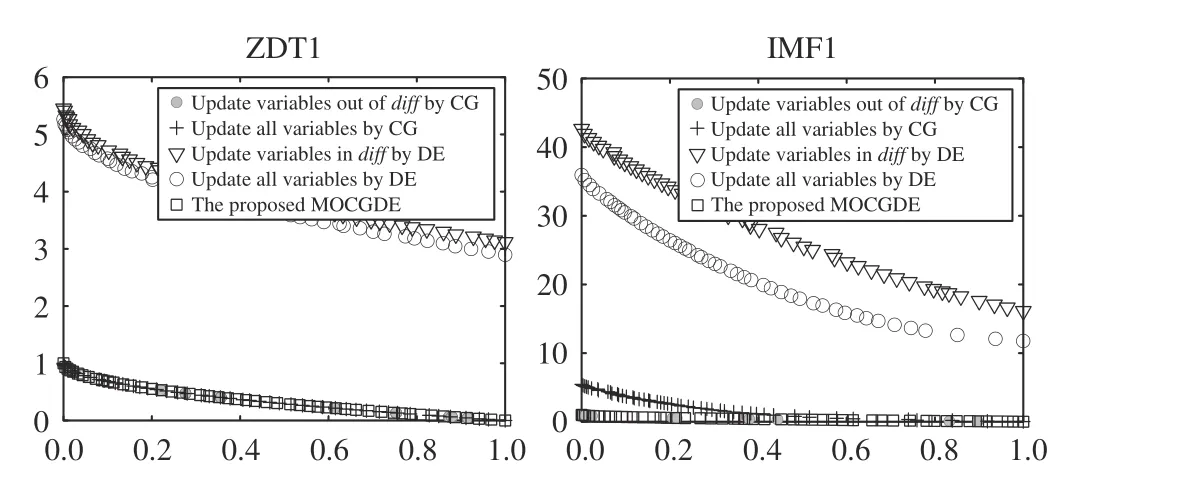
Fig. 8. Populations (in objective space) obtained by MOCGDE and its variants on ZDT1 and IMF1 with 1000 decision variables.
To study the influence of the population size on the performance of MOCGDE, Fig. 9 shows the IGD values of MOCGDE when the population size varies from 1 to 50. It is obvious that a small population size is effective for ZDT1 since a single optimal solution can be easily diversified to cover the whole Pareto front, while a large population size is effective for IMF1 since the spread of optimal solutions is hindered by the complex linkages between variables. As a result,the population size of 10 is the most suitable setting for MOCGDE.
V. CONCLUSIONS AND FUTURE WORK
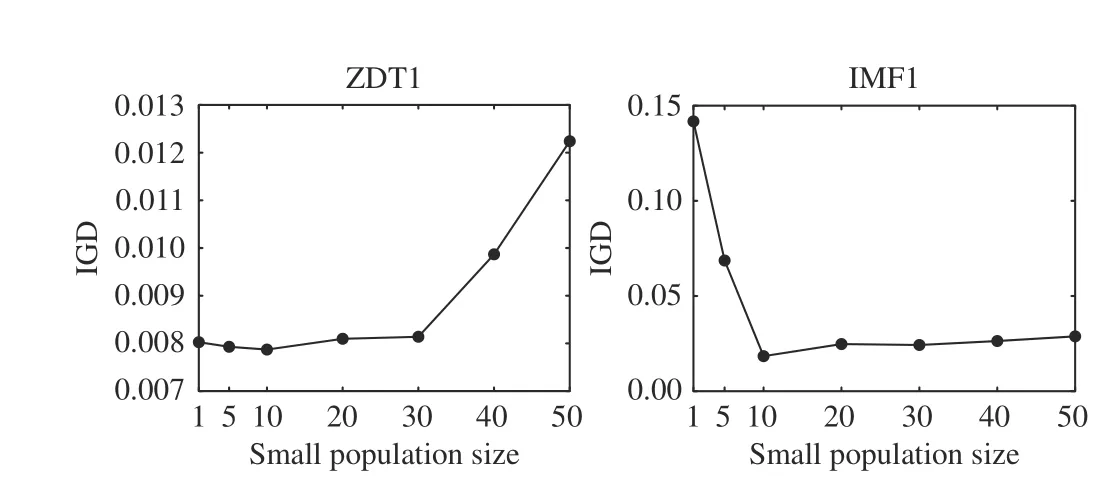
Fig. 9. Mean IGD values obtained by MOCGDE with different population sizes on ZDT1 and IMF1 with 1000 decision variables.
Currently, continuous LSMOPs are mostly handled by evolutionary algorithms, since they can find a set of diverse solutions in a single run [6]. However, existing evolutionary algorithms are criticized for slow convergence speed in huge search spaces, mainly due to the neglect of gradient information. Even for the objective functions whose first partial derivatives are unavailable, the gradients can still be approximated by finite difference. Therefore, this paper has proposed a hybrid algorithm by absorbing the fast convergence speed of mathematical programming and diversity preservation strategies of evolutionary computation. The proposed algorithm uses conjugate gradients and differential evolution to drive a small population towards the Pareto front, and maintains a large archive to store a set of diverse solutions found so far.The experimental results have demonstrated that the proposed algorithm is superior over existing evolutionary algorithms,mathematical programming methods, and hybrid algorithms on a variety of benchmark and real-world LSMOPs.
This paper has revealed the effectiveness of coupling evolutionary computation with mathematical programming for large-scale multi-objective optimization. In the future, more advanced evolutionary algorithms and mathematical programming methods can be considered to solve specific types of LSMOPs. For example, using the coevolutionary constrained multi-objective optimization framework [70] with the sequential quadratic programming [18] to solve constrained LSMOPs[2], using the multi-objective competitive swarm optimizer [9]with the Levenberg-Marquardt algorithm [17] to maximize receiver operating characteristics convex hull [71], and using the sparse multi-objective evolutionary algorithm [24] with momentum assisted gradient descent methods [12] to find sparse deep neural networks [20].
 IEEE/CAA Journal of Automatica Sinica2022年10期
IEEE/CAA Journal of Automatica Sinica2022年10期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Distributed Cooperative Learning for Discrete-Time Strict-Feedback Multi Agent Systems Over Directed Graphs
- An Adaptive Padding Correlation Filter With Group Feature Fusion for Robust Visual Tracking
- Interaction-Aware Cut-In Trajectory Prediction and Risk Assessment in Mixed Traffic
- Designing Discrete Predictor-Based Controllers for Networked Control Systems with Time-varying Delays: Application to A Visual Servo Inverted Pendulum System
- A New Noise-Tolerant Dual-Neural-Network Scheme for Robust Kinematic Control of Robotic Arms With Unknown Models
- A Fully Distributed Hybrid Control Framework For Non-Differentiable Multi-Agent Optimization
