A Wideband Microwave Holography Methodology for Reflector Surface Measurement of Large Radio Telescopes
Zan Wang, De-Qing Kong, Hong-Bo Zhang, Xin-Ying Zhu, Ze-Xin Liu, and Yu-Chen Liu
1 Key Laboratory of Lunar and Deep Space Exploration,National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100101,China;kdq@bao.ac.cn
2 University of Chinese Academy of Sciences, Beijing 100049, China
Abstract Most reflector surface holographic measurements of a large radio telescope utilize a geostationary satellite as the signal source.The shortcoming is that those measurements could only be done at a limited elevation angle due to the satellite’s relatively stationary state. This paper proposed a new wideband microwave holographic measurement method based on radio sources to achieve full-elevation-angle measurement with small size reference antenna. In theoretical derivation, the time delay and phase change due to path length and device difference between the antenna under test and reference antenna are compensated first.Then the correct method of wideband holography effect, which is because of antenna pattern differing under different wavelengths when receiving a wideband signal, is presented. To verify the proposed methodology, a wideband microwave holographic measurement system is established, the data processing procedure is illustrated, and the reflector surface measurement experiments on a 40 m radio telescope at different elevation angles are conducted.The result shows that the primary reflector surface root-mean-square at around elevation angles of 28°,44°,49°,and 75°are respectively 0.213 mm,0.170 mm,0.188 mm,and 0.199 mm.It is basically consistent with the real data,indicating that the proposed wideband microwave holography methodology is feasible.
Key words: astronomical instrumentation – methods and techniques – telescopes – methods: analytical –atmospheric effects
1. Introduction
In radio astronomy and deep space exploration, the aperture scale of a radio telescope is getting larger and larger.Meanwhile,the working frequency has also been highly promoted.Increasing working frequency brings big challenges to antenna metrology researchers due to the followed increased reflector surface accuracy requirement, according to Ruze (Ruze 1966). To determine the primary reflector surface accuracy of large radio telescopes, several metrology methods have been developed including theodolite-tape measuring (Greve et al. 1994), laser tracking (Gale 2012), laser scanning (Salas et al. 2020),photograph (Edmundson & Baker 2001; Gale et al. 2016), and holography (Rahmat-Samii 1985; Serra et al. 2012; López-Pérez et al.2014;Wang et al.2017,2019;Dong&Liu 2021).Among these diverse metrology methods,holography is believed to be the first choice in antenna’s routine inspection because of its high accuracy, fast speed, and low cost.
Looking into holographic measurement for large radio telescopes, we can find out that in practice, geostationary satellites have been widely used as the cooperative signal source (Serra et al. 2012;López-Pérez et al. 2014; Wang et al.2017;Dong&Liu 2021).Specifically,the cooperative signal in holography measurement is often a narrowband signal produced by geostationary satellites. The surface accuracy measurement of large radio telescopes could only be done at a limited elevation angle because of the facts that the satellites are stationary relative to the Earth and the number of geostationary satellites is limited. To achieve full elevation angle measurement, widely scattered radio sources can be considered as a substitute.
Signals coming from radio sources are usually quite weak compared with those transmitted from satellites. Therefore,they are easily embedded in the strong noises. To do holography based on radio sources, the signal-to-noise ratio(SNR)must be promoted first.One way to achieve high SNR is using a large aperture telescope as the reference antenna.However,the cost of a large aperture reference antenna is very high unless there is a large aperture telescope just near the antenna under test (AUT). Another very promising and convenient way to achieve high SNR is extending the observing bandwidth, which is feasible today by using a wideband receiver and data processing terminal. In other words,wideband holography would help reduce the size of the reference antenna.For instance,the reference antenna can be a 3 m diameter small dish in the wideband holography measurement of a 70 m radio telescope, when utilizing 3C273B as the signal source at X-band with a bandwidth of 1 GHz to achieve accuracy level of 0.1 mm with the resolution of 1 m. However, utilizing wideband signals for reflector surface accuracy measurement of a large radio telescope has not been theoretically or experimentally proved.This paper will demonstrate it by detailed theoretical derivation and primary designed experiments.
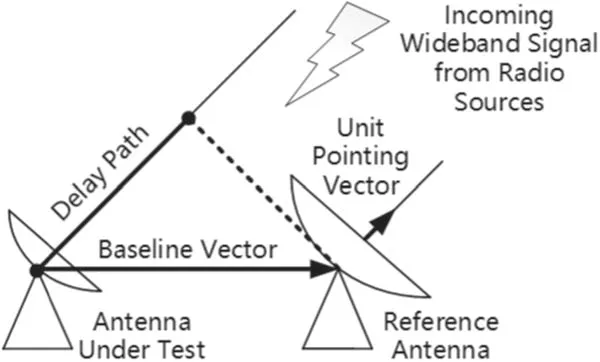
Figure 1. Theoretical delay path diagram.
The theoretical derivation of wideband microwave holography utilizing radio sources will be demonstrated in Section 2.A measurement system design and the corresponding data processing procedure will be introduced in Section 3. The measurement results and error analysis will be illustrated in Section 4. Finally, conclusions and prospects will be provided in Section 5.
2. Theories of Wideband Holography Utilizing Radio Sources
Theories of wideband holography utilizing radio sources can mainly be divided into two parts.One is the compensation of time delay and phase change due to path length and device difference between the AUT and reference antenna. The other is the derivation of wideband holography to correct the so-called wideband effect, which will be illustrated in detail in Section 2.2.
2.1. Time Delay and Phase Change Compensation
In holography based on wideband signal coming from radio sources,the time delay and phase change between the AUT and reference antenna is mainly caused by the path length difference induced by Earth rotation, and the device difference induced by cable bending.Figure 1 shows the theoretical delay path,which equals to a dot product between the baseline vector and the unit pointing vector. The theoretical time delay and phase change are caused by the delay path shown in Figure 1.
This paper divides the time delay into two parts, which are the integral and non-integral multiple of the sampling period.To eliminate the integral part for further calibration, we can calculate it in time domain based on the information including UTC time, the direction of radio source, and the location of AUT and reference antenna. To compensate for the nonintegral part, the cross correlation method can be used to calculate; and this compensation can be done in frequency domain. Together with phase change compensation, we can finally obtain the compensated signal of AUT in frequency domain as follows:
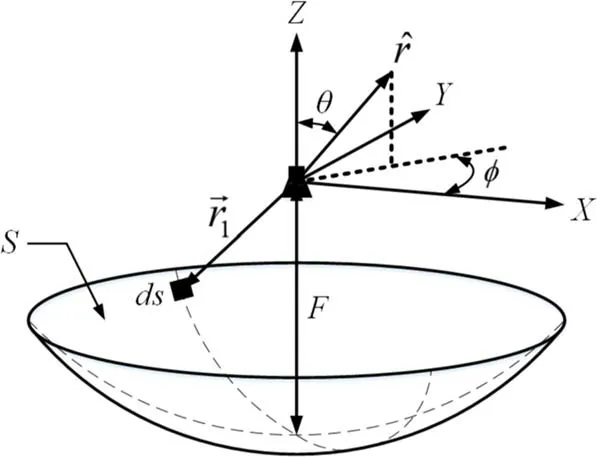
Figure 2. Paraboloidal reflector and the far-field distribution.
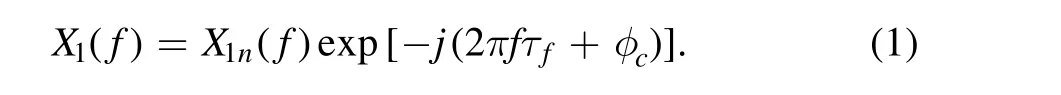
Here,φcis the phase change;τfis the fraction,non-integral,part of time delay;X1n(f)is the partly compensated signal with integral time delay eliminated;X1(f)is the totally compensated signal; j is the imaginary unit; and f stands for the signal frequency.
After the time delay and phase change compensation, we will be able to calculate the far-field pattern of the AUT by a cross correlation with X2(f), the reference signal. Specifically,the calculation formula is as follows:

2.2. Theoretical Derivation of Wideband Holography
The coordinate system of the reflector of a large radio telescope is defined in Figure 2. As for single-carrier and narrowband signals, the far-field pattern of a paraboloidal reflector illuminated by that will be (Reid 2008):


Here,θ is the zenith angle in the spherical coordinate system,i.e.,the angle between the unit vector ˆrand the Z-axis;φ is the azimuth angle in the spherical coordinate system,i.e.,the angle between the projection of the unit vector ˆron the XY plane and the X-axis;cosξis the paraboloid correction factor, namely

For a receiving signal with a bandwidth of B,after doing the accumulation of signals in the whole bandwidth, Equation (9)can be further written as:

To obtain the phase information, the above equation can be simplified into
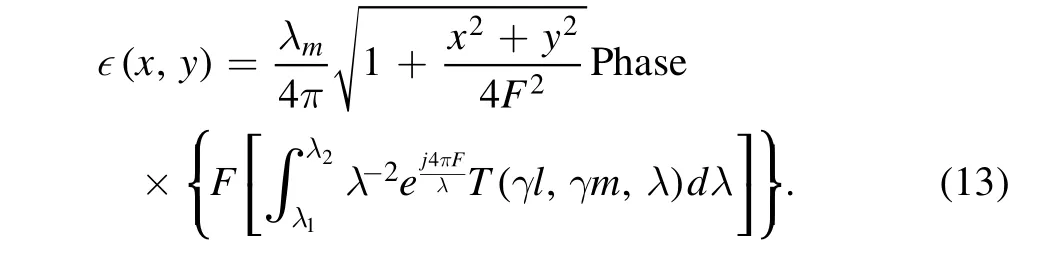
Here, F[...] stands for two-dimensional Fourier transform;Phase...is the symbol of phase calculation.Equation(13)is the final and core theoretical formula for wideband microwave holography.
Here,we also present a second version of the core theoretical formula for wideband microwave holography.
By shifting the item ej2kF, Equation (8) can be written as


Equation (18) is the second version of the core theoretical formula for wideband microwave holography. Compared with Equation(13),it is obvious that Equation(18)can help to reduce the complexity of accumulation of the far-field radiation function.
2.3. The Wideband Effect
For better understanding the advantages of above processing through different bandwidths,an example is given in this section.
As what we have mentioned in Section 2.2,the phenomenon of antenna pattern differing in amplitude and phase under different wavelengths when receiving a wideband signal is called the wideband effect.Now we consider what is the cost of not applying our wideband holography methodology when receiving a wideband signal.In other words,what final effect it would bring if the traditional holography methodology is applied regardless of the bandwidth. The surface error solving result under different bandwidths using traditional methodology can be simulated. Here are the assumptions before the simulation is carried out:
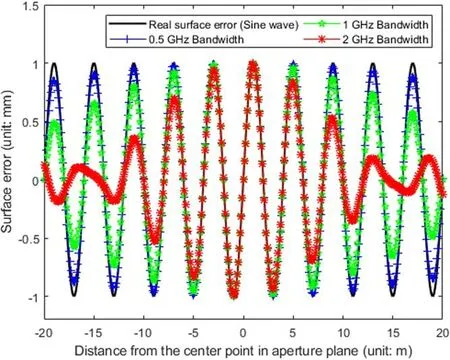
Figure 3. Surface error solving result under different bandwidths using the traditional methodology.
1. Considering the reflector surface is circularly symmetric,we can simply look into the one-dimensional situation of surface error solving.
2. Given a reflector with diameter of 40 m, a receiving signal with center frequency of 8.5 GHz (X-Band), we want to find out the surface error solving result under bandwidths of 0.5,1,and 2 GHz using the traditional holography data processing methodology.
3. The real surface error is set as a sine wave. For singlecarrier signal, the surface error solving result should be the same as the real. It should be noted that in our wideband holography methodology, Equations (13) and(18)in Section 2.2 help to do the accumulation of surface error solving results of a continuous series of singlecarrier signals, therefore, its surface error solving result should also be the same as the real.
Finally, the surface error solving result under different bandwidths using the traditional methodology is shown in Figure 3.
From Figure 3, we can see that the wideband effect would cause failure in surface error solving at places away from the center point. When bandwidth increases, the area of accurate surface error solving decreases. In traditional holographic data processing, due to the relatively small bandwidth (under 10 MHz), the surface error solving result will be very close to the black curve in Figure 3,and the wideband effect is minimal.To reduce the size of reference antenna, we proposed to use wideband signals for doing holography. Now the wideband effect should be seriously taken into consideration to avoid failures as the blue, green, and red curves shown in Figure 3.
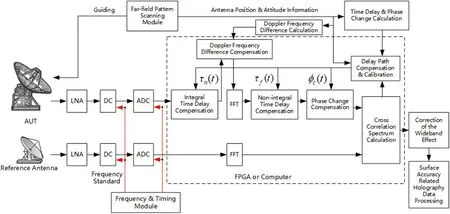
Figure 4. Wideband holographic measurement system diagram.
3. Measurement System Design and Data Processing Procedure
To verify the theories of wideband holography utilizing radio sources, a holographic measurement system is designed, and the data processing procedure is illustrated.It should be noted that the measurement system in this paper can also be applied for wideband holography utilizing geostationary satellites as the signal source.
3.1. Measurement System Design
The schematic diagram of wideband holographic measurement system based on radio source signal is shown in Figure 4. The system is composed of an AUT, a reference antenna, a digital integral time delay(τn(t))compensation module, a Doppler frequency difference compensation module, Fast Fourier Transform(FFT)modules,a non-integral time delay(i.e.,the fractional partτ f(t)) compensation module, a phase change compensation module, a cross-correlation spectrum calculation module, a time delay and phase change calculation module, a delay path compensation and calibration module, a far-field pattern’s wideband effect correction module, and an antenna refelctor surface accuracy related holography data processing module.
The far-field pattern scanning module is also presented in Figure 4. In holographic measurement, first, it is necessary to plan the movement of the AUT to scan its far-field pattern.The scanning diagram can be a butterfly style(Wang&Yu 2007)or any other central scanning style (Ren et al. 2020) (each scanning passes through the reflector center, as shown in Figures 5 and 6). For example, during the process of antenna scanning shown in Figure 6, we will be able to obtain the corresponding time delay and phase change at the center points of those blue solid arrows. The time delay and phase change information at those on-boresight moments will help to ensure that the change at other points can be accurately calculated for each scanning. Before the scanning starts, as the red dashed arrow shows in Figure 6, the AUT will be tracking the target radio source and then move rapidly to the start point of the planned scanning path once the scanning command is issued.As for the reference antenna, during the whole scanning process, it should always track the target radio source.
The scanning path planning of the AUT is realized by the far-field pattern scanning module in Figure 4. On the same time, the far-field pattern scanning module will constantly record the AUT’s status data, and convey it to the time delay and phase change calculation module,as well as the delay path compensation and calibration module for the calculation,calibration, and compensation of the time delay and phase change caused by path length and device difference between the two antennas.
3.2. Data Processing Procedure
3.2.1. Theoretical Time Delay and Phase Change Calculation
Theoretical time delay is the transmission time of a radio signal passing through the delay path, as shown above in Figure 1.The theoretical value of time delay can be calculated based on the following data:
1. The positions of two antennas, for obtaining the baseline vector;
2. The unit pointing vector of the reference antenna or the R.A. and decl. of the radio source.
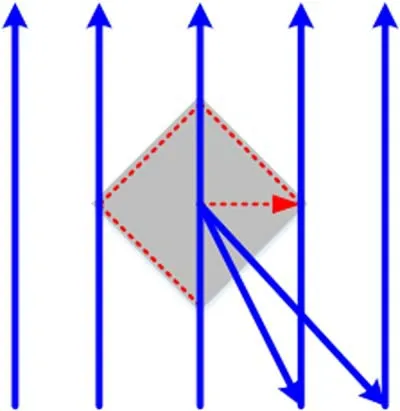
Figure 5. Butterfly-style scanning (Wang & Yu 2007).
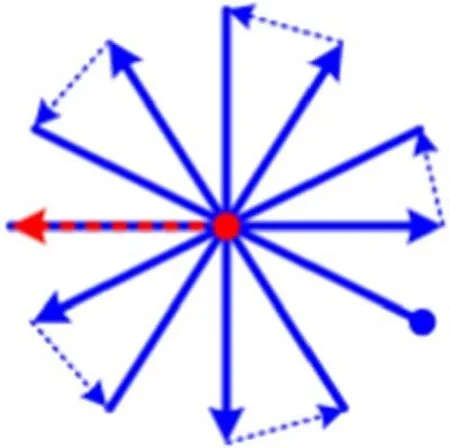
Figure 6. An Example of central scanning (Ren et al. 2020).
It should be noted that in practice, the position data of two antennas used for theoretical delay calculation are usually measured values which are believed very close to the actual ones.The unit pointing vector is provided by antenna log files.Besides, broadly speaking, the transmission path should include both of the spatial path and the cable path; but here in theoretical time delay calculation,only the spatial path delay is taken into consideration. The cable path delay is related to the cable length and changes along with different bending situation. In the following measured time delay calculation part, we will illustrate that.
By applying a dot product between the baseline vector and the unit pointing vector, we can obtain the theoretical time delay.Theoretical time delay should be a periodic function;and the period is a sidereal day. However, since the holography time is quite short, the theoretical delay curve probably looks like a straight line.Based on the theoretical time delay we have obtained, it is easy to get the theoretical phase change by multiplying 2πfm.
3.2.2. Measured Time Delay and Phase Change Calculation
During the process of antenna scanning,taking the scanning style shown in Figure 6 for example,we are interested in some on-boresight moments. These moments are:
1. At the beginning of holography. Before a scanning command is issued, both the AUT and reference antenna should be tracking the radio source for a short period of time. The red dot in Figure 6 can represent these moments.
2. At the intermediate instant of each scanning. The radio source should pass through the center point of each scanning. The center points of those blue solid arrows in Figure 6 can represent these moments.
By reading and searching the maximum of Rv values,generated by the power meter of the measured radio telescope,we will be able to get those on-boresight moments.In measured time delay and phase change calculation, we should focus on the measured delay path at those on-boresight moments. The measured delay path should include both of the spatial delay path and the cable delay path caused by temperature change,antenna rotation, cable bending, etc. Here, we look into the effects of the measured delay path from two different aspects,which are measured time delay and measured phase change:
1. Measured time delay.
The information of measured time delay, as well as the following measured phase change, is stored in the holography recording files generated by Radio Signal Recorder (RSR). By applying cross correlation and integral, we can get the measured time delay at each on-boresight moment. Then, by a comparison of theoretical and measured time delay calculation results, it will help us to better understand what happened in the cables and how much is the systematic error.
2. Measured phase change.
In microwave holographic measurement, compared with the sampling frequency, the center frequency of observation is often much higher. Therefore, the measured phase change calculation result is more accurate than the measured time delay result due to the much higher corresponding frequency. However, the value of measured phase at each on-boresight moment calculated from the holography recording files inevitably lost the information of the integer multiple of phase cycle,i.e., the 2πn part.
3.2.3. Phase Ambiguity Solving and Phase Change Curve Fitting
After the process of measured phase change calculation,there should be a followed procedure of ambiguity resolution due to the periodic variation of phase. In other words, the 2πn part, which has been mentioned above, should be studied. In this paper, we adopted the trial and error method to resolve phase ambiguity. The procedure is as follows:

Figure 7. The antenna under test.

Figure 8. The AUT and reference antenna.
1. Dividing. Find the remainder part of theoretical phase value at on-boresight moments.Divide 2πinto theoretical phase value at on-boresight moments obtained in Section 3.2.1, and record the remainder and quotient part, respectively.
2. Comparison. Compare the remainder part of theoretical phase value at on-boresight moments with the corresponding measured phase value obtained in Section 3.2.2.The gap between the two phase values should not be larger than π.
3. Ambiguity solving. Correct the 2πn part of measured phase.If the gap between the above two compared phase values is within π, assign the quotient part of the theoretical phase value to that of the measured phase. If the gap is larger than π,the quotient part of the theoretical phase value should add or subtract 1 before being assigned to the measured phase.
4. Phase calibration. Calculate the ambiguity-solved measured phase by adding the corrected 2πn part to the corresponding measured phase value obtained in Section 3.2.2.
Once the phase ambiguity is solved, i.e., the calibrated phases at on-boresight moments are obtained,the phase change during the whole scanning process can be fitted out. Base on the ambiguity-solved measured phase value at each onboresight moment, there are two main fitting ways to find out the phase for the further compensation procedure at other scanning points:
1. Sine fitting. Use a sine wave to fit all ambiguity-solved measured phase values at on-boresight moments. Record the four parameters,i.e.,amplitude,frequency,phase,and shift in the y-axis of the fitted sine wave.
Table 1 Positions of the AUT and Reference Antenna (Wu et al. 2022)
2. Piecewise fitting. Divide the ambiguity-solved measured phase values at on-boresight moments into several groups. Each group should have at least three or four members. Adopt the sine fitting method in each group.
3.2.4. The Far-field Pattern and Surface Accuracy Obtaining
Knowing the ambiguity-solved measured phase at each onboresight moment as well as the fitted phase for compensation at each corresponding scanning point, then, by eliminating those fitted phases for compensation from the measured phase at each corresponding scanning point and applying the equations we have illustrated in Section 2.1, the far-field pattern of the AUT can be obtained.
Once we got the far-field pattern of the AUT, the twodimensional Fourier transform will transform it into the reflector surface accuracy, as shown in Equations (13) and(18) in Section 2.2. The reflector surface accuracy distribution results,along with the results of the intermediate processes,are illustrated in the following part.
4. Experiment Results and Analysis
4.1. Experiment Results

Figure 9. Power distribution recorded by radio telescope’s power meter.

Figure 10. Comparison of theoretical and measured time delay calculation results.
The holographic measurement experiments are carried out according to the above theories, design, and data processing procedure.The 50 m radio telescope at Miyun station(Groundbased Radio Antenna Station 1, GRAS-1) is taken as the reference antenna. GRAS-3 40 m radio telescope is the AUT.The physical map of the AUT and reference antenna are shown in Figures 7 and 8.
To calculate the theoretical time delay and phase change,antenna position data is needed. The positions of GRAS-3 and GRAS-1 are given in Table 1.
In this paper, we find out the on-boresight moments according to the Rv values generated by radio telescope’s power meter. The power distribution measured at around the elevation angle of 44°, taken as an example, during the scanning procedure of the 40 m antenna is shown in Figure 9.Obviously, the scanning style in Figure 6 is adopted in our experiment.
The measured time delay calculation results compared with the theoretical ones are shown in Figure 10. The results at the elevation angle of 44°, taken as an example, indicate that the cable path difference,mentioned in Section 3.2.1,together with other systematic errors, is around 21 ns. After eliminating the average deviation, as shown on the right side in Figure 10, we can see that the measured time delay calculation results are consistent with the corrected theoretical ones.

Figure 11. The phase change curve fitting results for compensation.

Figure 12. Amplitude change in far-field.
In our holographic measurement, the sampling frequency is 50 MHz, while the center frequency(fm)of observation is 8,478 MHz (X-band). The receiving signal has a bandwidth of 40 MHz. In the process of non-integral time delay and phase change calculation, and compensation, the integration time is set as 838.8608 ms, which is exactly 256 times of the generation period of IF package.
In this paper, we adopted the trial and error method to resolve phase ambiguity, and apply the piecewise fitting method in calculating the phase for compensation. The phase curve fitting results for compensation during the whole scanning process at the elevation angle of 44°, taken as an example, are shown in Figure 11.
By eliminating those phase for compensation from the measured phase at each corresponding scanning point and applying the equations we have illustrated in Section 2,the farfield pattern of the AUT can finally be obtained.Figures 12 and 13 show the amplitude and phase change in far-field at the elevation angle of 44°, taken as an example.
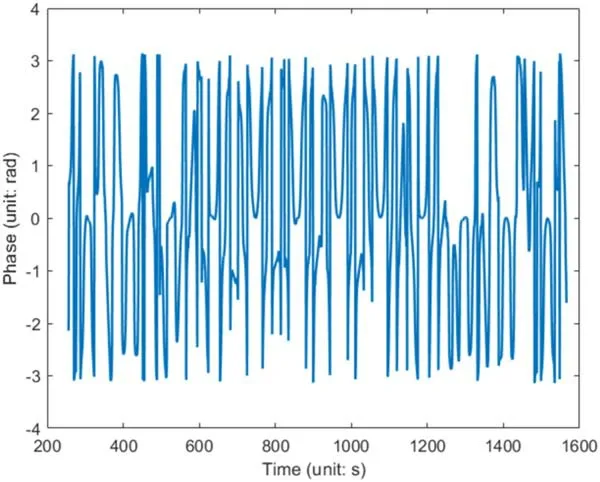
Figure 13. Phase change in far-field.
It should be noted that, in reality, the relationship between the offset of feed(sub-reflector)and aperture phase also need to be considered before fitting out the final cloud diagram of antenna’s primary reflector surface shape error (Butler 2003;Wang et al. 2019). Without eliminating that, the cloud diagrams of the 40 m antenna’s primary reflector surface shape error are shown in Figure 14.
The final fitting cloud diagram of the 40 m antenna’s primary reflector surface shape error is obtained,as shown in Figure 15.The surface root-mean-square (rms) at around elevation angles of 28°,44°,49°,and 75°are respectively 0.213 mm,0.170 mm,0.188 mm, and 0.199 mm, as shown in Table 2. The measurement time is around 26 minutes.
4.2. Error Analysis
The rms result is basically consistent with that obtained by photogrammetry done on 2017 April 19. In photogrammetry,the rms are 0.21 mm, 0.34 mm at elevation angle of 42°(optimal), 10°respectively. In our wideband holography measurement, the reflector surface shape error at around the elevation angle of 44°is relatively small. When the elevation angle decreases into around 28°or increases into around 75°,the reflector surface shape error becomes severe. It is basically consistent with the real data, indicating that the proposed wideband microwave holography methodology is feasible.However, compared with the designed surface distortion tolerance under ideal condition, the measurement results are influenced by the following factors:
1. Environmental noise.
Environmental noise interference is one of the main influencing factors for the experimental error of surface shape accuracy measurement. During the whole experiment,the power meter value is observed by the naked eye in real time to determine whether there is too much noise and need to terminate and remeasure.
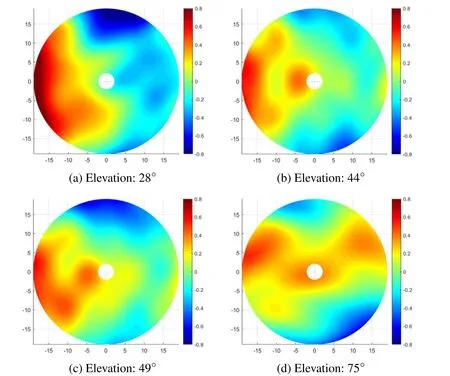
Figure 14. Reflector surface shape without eliminating the effects of sub-reflector offset (elevation at around 28°, 44°, 49°, and 75°).
2. Sub-reflector distortion.
One of the implied prerequisites for measuring the surface accuracy of the main reflecting surface of a large radio telescope by microwave holography is that the subreflector surface of the radio telescope must be nearly perfect. When the sub-reflector surface deviates from the ideal surface shape, the feeder at the main focus emits or receives a wave that is not the ideal spherical wave,resulting in a large systematic error in the surface shape accuracy measurement results.
3. Elevation angle change.
The reflector surface rms due to gravitational deformation varies at different elevation angles. Besides, unlike measuring the surface accuracy of a large radio telescope utilizing a geostationary satellite as the signal source, in this paper, the elevation and azimuth angle of the AUT change dynamically during the whole measurement. The elevation angle changes in Table 2 are 25°.95 ~30°.13,45°.55 ~42°.37,50°.09 ~48°.25,72°.78 ~77°.58 respectively.Therefore,to be precise, the holography using radio sources is a dynamic rather than static surface accuracy measurement.
4. Pointing accuracy.
Radio telescope pointing error is another major error source of microwave holographic measurement. Inaccurate pointing would not be able to guarantee the accuracy of on-boresight calibration, which finally leads to deviations between the calculated results of reflector surface accuracy and the true value. The pointing errors are caused by many factors, such as random wind load,insufficient lubrication of the radio telescope azimuth and pitch drive system, and delay in driver execution. The pointing of both GRAS-3 40 m and GRAS-1 50 m radio telescopes were calibrated before, and only a light wind was present during the experiment, so the effect of pointing errors on the results of our microwave holography measurement should not be significant.
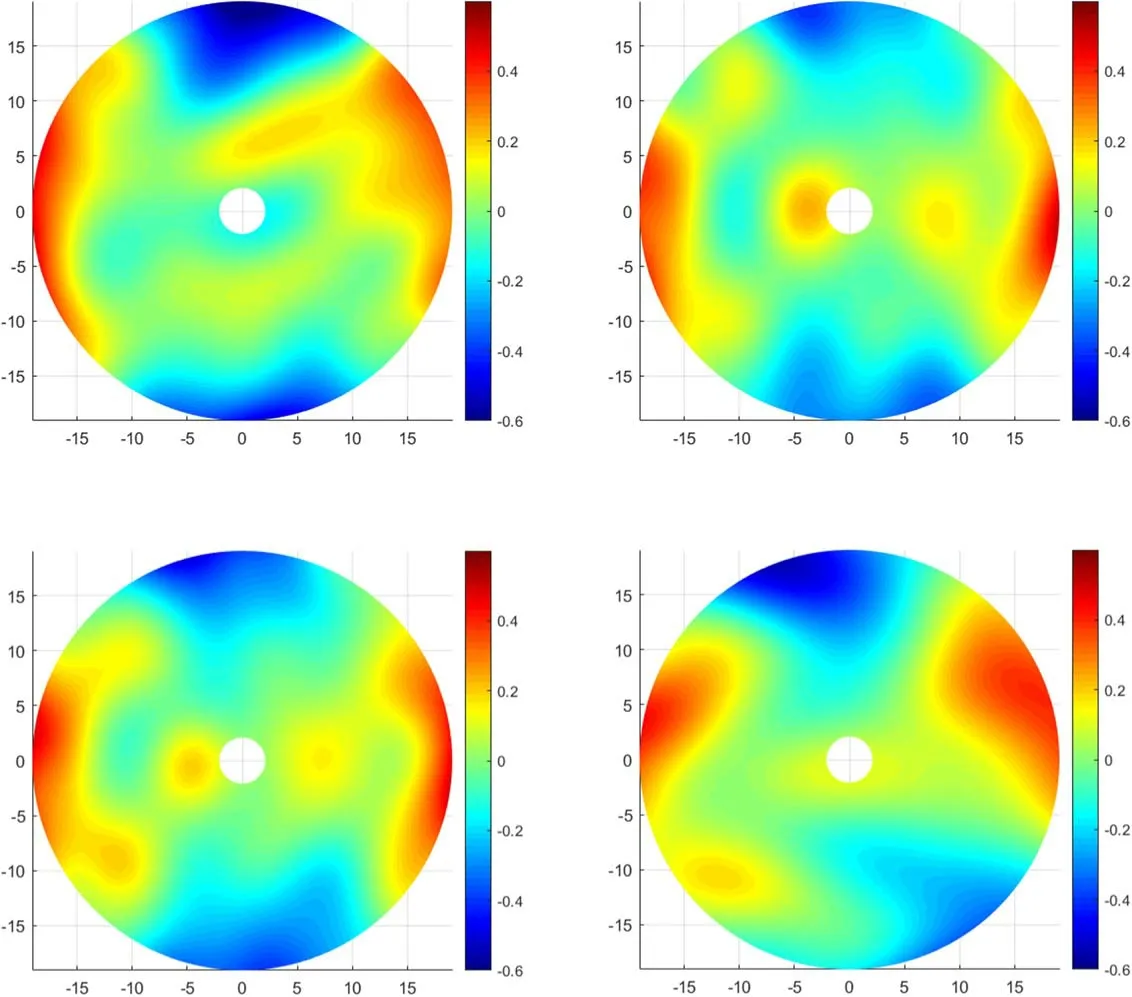
Figure 15. Reflector surface shape (elevation at around 28°, 44°, 49°, and 75°).

Table 2 Measurement Results
5. Atmospheric scintillation.
Atmospheric scintillation is also an important factor which can affect the accuracy of the surface shape accuracy measurement results. When the measured radio telescope and the reference radio telescope are close to each other, it can be generally assumed that the electromagnetic wave path is basically the same. Our AUT and reference antenna are on the same observatory station and not far from each other, therefore, the electromagnetic wave path is almost identical. However,when the Earth’s ionospheric, stratospheric, and tropospheric environments become unstable, i.e., when atmospheric scintillation is more significant, the accuracy of the radio telescope surface shape calculated according to the original assumption of stability is no longer accurate.
6. Temperature and humidity.
Temperature rise will lead to the surface distortion becoming severe. The microwave holographic measurement experiment was conducted on August 19 and 21. It is better to do the experiment in the late evening on summer. On August 20, it rained a little. The reflector surface of our radio telescopes is checked and believed dry on the second day, so the influence of humidity should not be significant.
7. Scanning model
. The scanning model applied in this paper is nonuniform scanning, and the aperture resolution is high internally and low externally.This would lead to different distribution of measurement errors. Qualitatively, the measurement error is proportional to the area of the annular sector, which increases from the center to the edge of the aperture.
5. Conclusion and Prospect
In this paper,by accurately compensating and correcting the time delay and phase change caused by the delay path and device difference between the AUT and the reference antenna,and by correcting the difference of the far-field pattern caused by the wideband effect, a wideband microwave holography methodology is proposed and demonstrated in detail.To verify the methodology,a measurement system and the corresponding data processing procedure are designed. Some experiments are carried out by using the 40 and 50 m antennas as the AUT and reference antenna. The reflector surface measurement results indicate that our wideband holography measurement method is feasible.
In further research, for the wideband holography of a large radio telescope,the observing bandwidth can be extended to at least 1 GHz. And the size of the reference antenna can be reduced with a diameter within 3 m. The panel resolution will be improved within 1 m.
Acknowledgments
This work was funded by the Astronomical Joint Fund of the National Natural Science Foundation of China and Chinese Academy of Sciences (Grant Nos. U1831114, 11941002, and 12073048).
 Research in Astronomy and Astrophysics2022年9期
Research in Astronomy and Astrophysics2022年9期
- Research in Astronomy and Astrophysics的其它文章
- YFPOL: A Linear Polarimeter of Lijiang 2.4m Telescope
- Pre-explosion Helium Shell Flash in Type Ia Supernovae
- A Region Selection Method for Real-time Local Correlation Tracking of Solar Full-disk Magnetographs
- Research on the On-orbit Background of the Hard X-Ray Imager Onboard ASO-S
- Chinese Sunspot Drawings and Their Digitization—(VII) Sunspot Penumbra to Umbra Area Ratio Using the Hand-Drawing Records from Yunnan Observatories
- Supergranular Fractal Dimension and Solar Rotation
