修复断层 拨正误区 突破难点——《认识时间》教学实践与思考

文|魏欢 曹炯 金勤

【课前思考】

一、纵向梳理，把握教材前后脉络

1.一年级《认识钟表》与二年级《认识时间》衔接情况。

钟面结构认识上存在断层：一年级只认识了12 个数字和时针分针，二年级直接就出现“小格”“大格”的概念，而对于钟面上一小格、一大格的定义均未做出相应解释。

认读时刻方法上存在差异：一年级对于整时认读描述的语言是静态的——分针指着12，时针指着几，就是几时。二年级则趋向动态描述，分针时针都动起来了，这一细微的差别蕴含着强大的思维挑战。

时针分针联动原理上存在盲点：一年级学生只是静态认识了整时、几时刚过以及快几时了，并没有强化分针和时针联动的过程，对二年级的学习产生了盲点。

2.二年级《认识时间》与三年级《时分 秒》衔接情况。

三年级《时 分 秒》单元由时、分的单位转换至分与秒，在二针联动的思维基础上类推至理解三针联动关系，形成动态钟面模型。此阶段教材编写更多侧重于学生对时间概念的理解，开始有明确的“推测时间量”的活动。在时间概念理解上，一、二年级为三年级的学习奠定基础；在时间观念的建立上，一、二年级教材几乎没有为三年级体验时间量做铺垫。

二、了解学情，精准定位教学目标

二年级学生在学习本节课时，已经掌握了时针、分针等钟面组成部分，也理解了整时，在其生活经验中也已具备一定的快到几时、几时刚过的概念。但经过两个教学班的教学实践后，发现学生还存在以下几个问题：学生对于钟面上数字背后所代表的分钟数还不太清晰；学生对时针、分针运动的区别和联系掌握不清；学生最容易做错的是几时55 分，他们往往会将9 时55 分看成10时55 分。

基于以上分析，在本节课的教学设计中，笔者有以下几方面的思考：

1.修复断层。

关于钟面结构，一年级已经认识时针、分针以及12 个数字。本节课首先对钟面结构进行再认识——小格、大格的认识。小格对应“1 分”，大格对应“5分”，将这部分内容融入在“分”的教学中，强化分针走1 小格是1 分、走1 大格是5 分的概念。同时，钟面上12 个数字所代表的分钟数也是学生在认识时间的过程中需要重点掌握的。学生会直观地认为分针指着几就是几分，因此需要动态演示分针运动过程让学生深刻感知。在认识分钟数的方法上，1 分1 分数、5 分5 分数、乘法口诀等都应给予认可，让学生自主感知每种方法的优越性。

2.拨正误区。

学生在一年级认识整时的学习，是静态且分离的，对于时针和分针联动的概念是缺失的。因此，在本节课中可以通过钟面动态演示，让学生体会分针与时针的均匀联动，破除“时针指着几就是几时”的惯性思维，感知时与分两个时间单位间的联系（1 时=60 分），二者是一个整体，不可分离，能够在动态钟面中正确判断出静态结果。

3.突破难点。

几时55 分的认识是本节课的重难点。学生在认读55 分的静态钟面时，往往会认读成下一时刻，这是由于学生的头脑中对时与分的内在联系仍没有形成表象。课堂中可以结合动态演示，点出分针走55分，时针从几开始走，慢慢地走向下一个时刻，看上去时针指着几+1 这个时刻了，但是还没有走到，只有当分针走满60 分钟，时针才会正好指向下一个数字。要让学生充分学会用这种动态的思维分析静态的钟面。

4.联系生活。

对低段学生而言，时间是一个抽象的概念，对时间的感觉是需要与具体的生活事件联系的。因此时间的教学不应始于课堂，而是要贯穿在学生的生活之中，课前渗透、课后应用，让时间在成为知识点之前，先成为学生的生活经验。

【教学过程】

一、复习钟面，回顾整时

师：你们都认识时间吗？那老师要来考考你们！

（课件依次呈现）

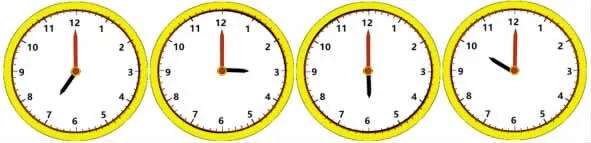
师：你们都说最后这幅图上是10 时，你是怎么看出来的？

二、探讨新知，突破知识难点

1.自主探究，初识时间。

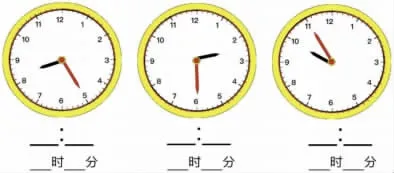
2.初探认时间的方法（分）。

师：对于第一个钟面，说说你是怎么看的？（预设：8:5、8:50、8:25）分享想法，产生分歧，引导进入“分”的认识。

师：观察钟面上的分针，分针走1 小格是1 分（板书），那继续走呢？5 小格在钟面上也就是1 大格，分针走1 大格是5 分（板书）。

师：如果分针再往前1 小格，你知道是几分吗？

师：走1 大格是5 分钟，那么走到2 呢？走到3呢？你是怎么看出来的呀？

师：分针走到8 是几分？你是怎么看的？

师：分针走到8 是40 分，那如果接下来分针再往前走1 小格，是几分？那再往前走1 大格呢？

追问：分针从12 出发回到12，走了整整一圈，经过了几分钟？所以说，分针走一圈是60 分钟（板书）。

教师随机指钟面数字，学生说出对应的分钟数。

3.初探认时间的方法（时）。

师：你现在知道它是几时几分了吗？（8 时25 分）

追问：8 时25 分时针不应该是指着8 的吗？（分针动的时候时针也在动）

动态演示：分针从12 开始重新走1 大格，时针有什么变化？（时针动了一点点）走到6 时，分针走了半圈，那时针呢？（时针走到8 和9 中间）如果这个分针继续往后走，向12 靠近，时针会怎么变化？（向9 靠近）如果分针转一圈回到12，时针又会怎么样呢？（正好指向9）

小结：分针走一圈的同时，时针走了一大格。（板书：1 时=60 分）

出示2:30 的钟面：通过刚刚的学习，你现在知道这是几时几分了吗？

4.突破难点9:55。

师：你们觉得它是几时几分呢？（预设：9:55，10:55）说说你是怎么看的。

师：（动态演示）分针走到55 分时，时针是从哪出发的？这时的时针有没有到10，为什么说时针还没到10 呢？

对比演示10:55，巩固55 分的认识。追问：11：55，时针指向哪里？

师：让我们再来看看，它是几时55 分，为什么？

再次演示：从4:00 开始走，分针转动过程中，时针会怎样变化呢？（指名多人叙述）

最后得出结果：4：55。

三、巩固练习，内化知识要点

1.作业本第64 页第一题（改编）：你是怎么看出时间的？

2.9：□□，下面哪些钟面可能是这个时间？你是怎么看的？

提示：这个分钟数很大，现在你能知道哪个时钟是这个时间了吗？

□：10，下面哪个时钟可能是这个时间？你是怎么看的？（6:10，3:10 都可能）

4.合理安排时间（略）。

四、课堂总结

请学生说一说在认读几时几分时需要注意什么？一起来归纳总结本课所学内容。

【课后思考】

1.了解学生学习需求，精准定位教学目标。

课前教师了解学生的经验基础至关重要。二年级的认识时间是在学生已经熟悉钟面结构，并能熟练认读整时的基础上进行的，本课的教学应该聚焦在时刻认读上。所以，导入环节采用有利于调动学生学习积极性的游戏方式来唤醒学生头脑中对于认读时间的知识经验。

2.明确学生疑点难点，深度体验知识建构。

学生对于新知识的前概念大多来源于直接经验，这其中会存有偏差，如果教师在教学中没有发现或一笔带过，那么学生的进一步学习将会被阻碍。因此，明确学生的疑点难点是学生进一步学习的基础，也是将学生思维推向更深层次的关键。

在一年级的整时认读教学中，通常学生会机械地记住：分针指着12，时针指着几就是几时。这种方法直观、清晰，学生也易于掌握。但是这种静态的观察方式割裂了分针与时针之间的关系，忽视了时间永动的特性，两针联动的动态概念在学生的头脑中是缺失的，这也是本节课继续学习的最大障碍，也是导致学生认读几时55 分容易出错的主因。因此，教师在课中要有意识地强调联动的概念，通过多次动画演示加深印象，力求让学生从分离的思维定式走向整体思维。操作性的活动是学生学习知识的有效途径，学生自己去操作，在学具钟面上拨一拨，对引导学生体验并感悟时刻的形成过程有一定的积极意义。

二年级学生理解同步联动有一定难度，这就需要教师在教学中重点攻坚，持续渗透。从教材的安排来看，认读钟表分为三个阶段，同步联动的观念渗透从一年级的“认识钟表”就应该开始了。对于时针和分针同步运动，这点学生很容易就能感知到，不仅如此，许多学生还能认清两者的速度不同，但这并不代表学生理解了时针与分针的联动性。譬如“8：00”，一般解说为时针正好指向8，分针正好指向12 就是8：00。这是一种用静止的眼光观察钟面得出的结论。改用动态的视角来描述应为：时针走到8 的位置，分针恰巧再次来到12，此刻正好是8 时整。这样就能让学生在静态读数时启动动态推演思维。

3.挖掘学生生活经验，充分体会知识价值。

数学源于生活也归于生活，关于时间，学生在生活中会慢慢形成自己的生活经验，这种经验如何转化为数学知识，更是我们教师需要思考的。我们不仅要教会学生时刻的认读，更要让学生理解它是怎么来的，为什么是这个时间。朱国荣老师与胡慧良老师都为时间教学给出了指引：认识时间的教学不应该始于这个单元这堂课，而应贯穿于学生的学习与生活。带有时针和分针的钟表在家里和教室里都有，每天在家的生活和在校的学习中，认识时间的学习已经慢慢展开了，而课堂活动应是学生生活经验的梳理和升华。

时间属于小学数学常见量中的一种，那么认识时间属于哪个学习领域呢？《数学课程标准（2022 年版）》将认识时间归于“实践与综合应用”板块，采用主题学习和项目化学习的方式进行。这为我们的教学指明了方向，认识时间板块更适合在活动中进行，将时间学习融入生活，从中体会时间与生活的密切联系，在生活中积累经验，并转化为数学知识，形成时间概念，这是一个真实且高效的学习过程。