基于改进粒子群算法的储能优化配置

温春雪 赵天赐 于 赓 王 鹏 李建林

基于改进粒子群算法的储能优化配置

温春雪 赵天赐 于 赓 王 鹏 李建林

（北方工业大学北京市变频技术工程研究中心，北京 100144）

储能将功率在时间维度上进行转移，可以抑制电压波动，减小网络损耗。为了合理地配置储能，以改进多目标粒子群算法为基础，建立一种以电压波动率、网络损耗和配置成本为优化目标的储能优化模型。在粒子初始化阶段，通过增加初始粒子个数，挑选出分散的非支配优势粒子作为初始种群，来提高初始种群的随机性；在速度更新阶段，采用节点电压指导粒子的进化方向，提高算法的计算速度。采用IEEE-33节点算例的仿真结果表明，对粒子群算法的改进提高了算法的稳定性、计算速度和精度；采用改进算法的储能配置方案，降低了系统的节点电压波动，减小了电能损耗。

配电网；改进粒子群算法；储能配置；多目标优化

0 引言

合理地配置储能可以解决新能源并网带来的一系列问题[1]，对于提高电能质量[2]、降低网络损耗[3]具有重要意义。目前储能的配置成本高、投资回收期较长，且我国颁布的激励政策尚不完善[4]。上述因素一直是限制储能发展的主要原因，储能的合理规划配置对于储能行业的健康发展意义重大。

为了使储能的配置方案最优，目前的主流方法是采用智能算法，基于确定的应用场景建立储能优化配置模型[5]。储能优化配置问题一般以储能配置位置、容量和各时刻储能充放电功率作为决策变量，其中储能配置位置为非线性变量。由于决策变量的设定，决定了电网侧储能优化配置问题需要同时考虑储能的选址和定容两个方面[6-7]。文献[8]提出配置储能可以减小系统网络损耗，并以此作为储能选址的依据。文献[9]在储能削峰填谷的应用场景下，建立了以综合成本最小为优化目标的储能优化配置模型。文献[10]同时考虑储能参与系统调频的经济性指标和技术性指标，建立了以系统总调峰成本最小为优化目标的储能优化模型。因为决策变量中储能充放电功率要受储能容量的约束，所以决策变量中各元素之间相互影响和制约。目前针对储能优化配置问题，考虑决策变量各元素之间影响的研究较少，对其展开研究对于提高储能配置算法的性能具有重要意义。

在算法选择方面也涌现出很多优秀的智能算法。文献[11]采用遗传算法，建立了多元储能电站的优化配置模型。文献[12]采用粒子群算法，考虑储能在运行过程中的寿命衰减，进行优化计算。文献[13]基于改进多目标粒子群算法（multi-objective particle swarm optimization, MOPSO）对储能系统进行选址定容。目前已有改进粒子群算法如模拟退火算法、引入线性权重、引入自适应惯性权重等改善了算法的性能[14]。文献[15]采用改进多目标粒子群算法进行储能配置计算。文献[16]采用模拟退火改进算法，构建包含储能的综合能源优化运行模型。上述研究对算法进行了改进，在一定程度上避免了算法容易陷入局部最优的问题。但是改进部分仅针对算法速度更新公式中的参数，未能合理利用储能配置过程的系统信息。上述研究还存在种群数量不足、容易陷入局部最优的问题。

本文针对储能优化配置问题，对MOPSO的粒子初始化过程和速度更新过程进行改进。在粒子初始化阶段，增加初始粒子数量，选择少量优势粒子参与迭代，增加算法的稳定性；在速度更新阶段，考虑解各维度之间的制约关系，采用节点电压指导速度更新过程，提高算法的计算速度。最后通过仿真对比常规MOPSO和改进MOPSO，证明改进MOPSO算法的优越性。改进算法的配置方案在成本更低的情况下，对于系统电能质量和网络损耗的改善效果更好。

1 新能源出力模型与储能模型

1.1 新能源出力模型

目前优化算法普遍采用时序运行仿真方法，以对应时段的新能源及负荷数据为基础，进行储能优化计算。为了更好地模拟新能源出力，本文建立包含随机性的新能源出力模型。通过自回归滑动平均法生成场景，然后采用基于概率距离的场景削减 法[17]，最终确定新能源出力曲线，具体步骤如下。

1）根据自回归滑动平均公式生成新能源出力曲线，将出力曲线加入场景集合1中。

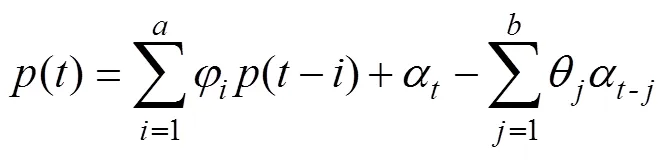
2）为了避免大规模场景造成的计算困难，采用场景削减法，将场景集合1削减至2。

自回归滑动平均法和基于概率距离的场景削减法确定新能源出力曲线的流程如图1所示。

图1 新能源出力场景生成流程

1.2 储能模型

为了体现储能容量与储能各时刻充放电功率之间的约束关系，通过等式约束将储能的存储电量与充放电功率联立，建立储能模型。当储能充电时，储能系统电量为

当储能系统放电时，在时刻储存电量为

式中：e()为时刻储能的电量；D为仿真步长；e()为时刻的储能充放电功率；c和d分别为充、放电效率。

2 储能优化配置模型

本文以降低节点电压波动为优化目标，采用网络损耗作为储能选址的依据，同时为了保证配置方案的经济性，又选取配置成本作为储能优化配置的目标函数。基于改进MOPSO，构建多目标储能优化模型。在粒子初始化阶段和速度更新阶段对算法进行改进。

2.1 优化目标

1）节点电压波动

由于新能源的出力特点，新能源接入电网后造成节点电压波动，增加网络损耗。因此，以节点电压波动作为储能优化配置的目标函数，公式为

2）网络损耗

在相同负荷水平下，网络的有功损耗会随着功率的波动而增加，以网络损耗最小为优化目标，可以表示为

3）系统成本

储能系统成本包括储能建设成本和运行成本，其中储能建设成本包括储能容量成本e和储能功率成本p，则有

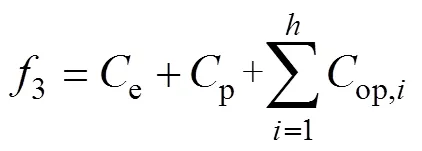
式中，op为储能运行成本。

本文以1、2、3最小，设置储能优化模型的综合优化目标为

2.2 约束条件

1）节点电压约束

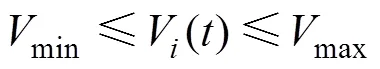
式中，min、max为节点电压的下限和上限。

2）功率平衡约束

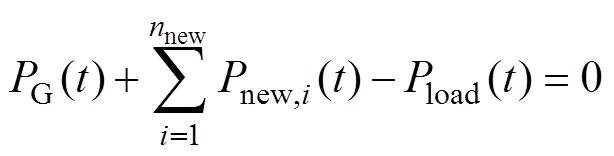
式中：G()为发电机组有功出力；new为分布式电源的安装个数；new,i()为第个分布式电源在时刻的有功出力；load()为时刻系统的总负荷。

3）储能功率约束

3 多目标改进粒子群算法模型

3.1 多目标粒子群算法

对于惯性权重的取值，采用线性递减惯性权重，计算公式为

粒子群算法在解决单目标优化的问题中表现优异，但是多目标优化问题的解是几组连续解的集合，无法通过粒子群算法直接求解。MOPSO将求出的互不支配的解保存在Pareto解集中，求解出一系列非劣解。在这些非劣解中选取全局最优和历史最优解，指导粒子的进化。

利用MOPSO进行储能系统的优化配置时，存在以下问题需要改进：

1）粒子维度过高，迭代过程中容易陷入维度陷阱。增加种群数量可以解决这个问题，但又会导致计算量和计算时间大大增加。

2）在优化求解储能实际问题时，未充分利用相关信息指导粒子进化过程。采用系统节点电压来指导粒子进化，能极大改善算法的性能。

3.2 改进多目标粒子群算法

本文提出的改进MOPSO在粒子初始化阶段，提高初始粒子数量；在速度更新阶段，利用节点电压指导粒子的进化方向。在增加很少计算时间的前提下，可改善算法的性能。

1）粒子初始化

粒子群算法依靠随机性来求解问题，但是随着解维度的增加，需要增加粒子的数量来保持随机性。储能优化求解问题，决策变量通常设置为=(1,2,3,4,…,26)，决策变量的维度为26维。其中1为储能配置位置，2为储能配置容量，3,4,…,26为各时刻储能动作功率。足够大的种群数量，才能使粒子在一个26维的高维空间中保持随机性。但是受到算力和计算时间的限制，一味地增加种群数量并不现实。

为了增加粒子的随机性，本文在粒子初始化阶段，对算法进行改进。首先随机生成大量粒子，并计算其目标函数，该目标函数与算法实际优化目标相同。然后对粒子进行非支配排序。挑选出密度距离大的优势粒子，作为初始种群的一部分。在粒子初始化阶段对算法的改进不但保证了初始种群的分散性，而且筛选出了优势粒子。初代种群的质量会极大地影响算法的迭代更新过程，通过改进不仅能提高算法的稳定性，还能提高计算速度。

粒子初始化过程示意图如图2所示，随机生成100个粒子，并筛选出5个分散的优势粒子，将其与随机生成的5个粒子一起作为初始种群，如图2（c）所示。对比图2（c）、图2（d）可以看出，对粒子初始化过程的改进使初始种群更加分散，且粒子的目标函数更接近最大值。

图2 粒子初始化过程示意图

具体计算过程如下：

（1）设置种群个数1、初始种群个数为2，其中21，初始粒子选择百分数。

（2）初始化生成2个粒子，然后计算其目标函数值，并按照目标函数值对2个粒子进行非支配排序。

（3）得到Pareto解集，Pareto解集大小为，并对Pareto解集按照密度距离大小进行排序。

（4）选择排名前1个粒子加入初始种群，再随机生成(1-b)1个粒子作为初始种群。若小于1，则随机生成1-个粒子作为初始种群。

2）粒子进化

在储能优化配置的实际问题中，一些参数可以指导粒子的进化方向。电网侧配置储能可以利用节点电压指导粒子的进化过程。当节点电压过高时，储能应该吸收功率，储能充电的概率更大；节点电压过低时，储能应该发出功率，储能放电的概率更大。因此，可以利用节点电压来指导粒子的进化过程，从而提高算法的计算速度。

但是采用节点电压来指导粒子进化，会因为人为干预，导致算法陷入局部最优。所以引入触发概率trigger_，随着迭代次数的增加，算法触发指导粒子进化的概率减小。

决策变量中储能容量制约着储能各时刻功率的大小，又因为优化模型采用时序仿真的方法，即第一个时刻储能的动作功率3确定后，再验证4是否满足储能容量的约束。所以，储能功率对应时刻越小，对于解的正确性越重要。因此本文引入触发概率trigger_，随着时序仿真时间的增加，算法触发指导粒子进化的概率减小。

具体步骤如下：

（1）本文选用节点电压作为判断储能充放电动作的指标，即先计算未配置储能时，所有节点各时刻的电压标幺值，作为判断储能动作的依据。

若当前时刻节点电压小于该节点各时刻电压的平均值，op-fc=1；若当前时刻节点电压大于该节点各时刻电压的平均值，op-fc=-1。

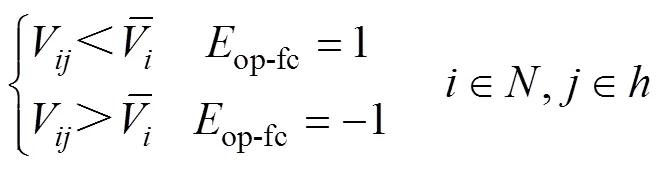
式中：V为节点在时刻的电压；op-fc=-1代表当前储能动作为充电是最优解的概率更大；op-fc=1代表当前储能动作为放电是最优解的概率更大。

（2）判断储能实际动作方向，即规定储能动作功率值为正，op-re=1；储能动作功率值为负，op-re=-1，表示为

（3）判断储能动作指标op-re与op-fc指标计算出的希望储能的动作功率是否相同，如果不同，则进行下一步判断。

若op-fcop-re=1，则触发进化方向修正机制；若op-fcop-re=-1，则不触发进化方向修正机制。

（4）第（3）步已经判断了op-re与op-fc异号，说明e()与期望的储能动作方向相反。若此时v()与e()方向相同，则使e()向着与期望的储能动作相反的方向进化，而粒子向着期望的储能动作方向进化，粒子为最优解的概率更大。

当v()op-re＞0时，进行下一步判断；当v()op-re＜0时，不触发进化方向修正机制。

（5）设置迭代次数触发概率函数trigger_，所述迭代次数触发概率函数trigger_随着迭代次数的增加由最大触发概率timax递减到最小触发概率timin。

迭代次数触发概率函数trigger_表示为

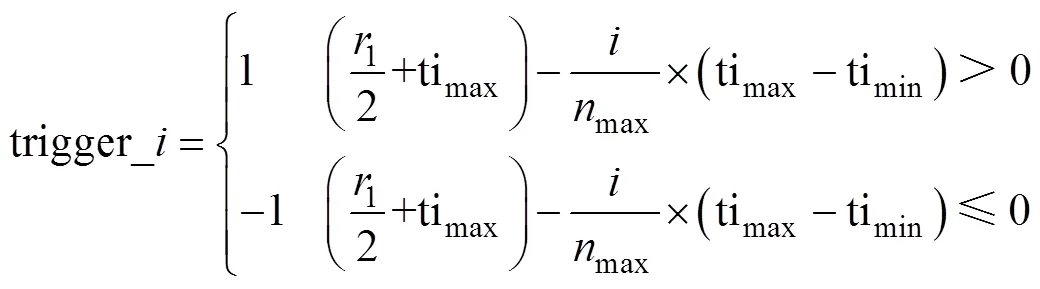
式中：1为值域[-1, 1]的随机数，1的选取是利用粒子群算法所需的随机数，不需额外生成随机数；为当前迭代次数。

这里设置迭代次数触发概率函数trigger_是为了防止算法陷入局部最优，人为干预影响算法的计算准确性。该算法按一定概率触发，随着迭代次数的增加，触发的概率降低，逐步放开对粒子进化方向的限制，trigger_的值为1，触发概率函数；trigger_的值为-1，不触发概率函数。

（6）设置仿真时间触发概率函数trigger_，随着仿真时间的增加由最大触发概率thmax递减到最小触发概率thmin。

仿真时间触发概率函数trigger_表示为

式中：2为值域[-1, 1]的随机数，2的选取是利用粒子群算法所需的随机数，不需额外生成随机数，为了避免耦合，1和2选用两个不同的随机数；为当前储能动作时间。

决策变量 (3,4,…,26) 中各时刻储能动作功率，前面时刻数值的准确性对粒子整体准确性的影响更大。所以设置仿真时间触发概率函数trigger_，随着时序仿真时间的增加，该算法触发的概率降低，降低人为干预对粒子进化方向的影响，避免局部最优。同样，trigger_的值为1，触发概率函数；trigger_的值为-1，不触发概率函数。

（7）综合判断，当op-fcop-re=1、v()op-re＞0且trigger_与trigger_都为1时，触发进化方向修正，即

粒子速度更新修正流程如图3所示。

3.3 Pareto解集更新与全局最优的选择

Pareto解集用来存放算法迭代过程中产生的非劣解。为了维持Pareto解集的规模，并保证解集分散性，当解集规模超过规定值后，要将Pareto解集中密度距离最小的解淘汰。将Pareto解集进行非支配排序后，密度距离()为

式中：xi为Pareto解集中第i个非支配解；为第i个粒子的第j个目标函数值；为第j个目标值的最大值；n为目标函数个数；m为Pareto解集规模。

在计算全局最优时，计算Pareto解集中各粒子的密度距离并进行排序，从粒子密度距离较大的前20%中随机选取一个粒子，作为种群全局最优解。

3.4 基于TOPSIS的多属性决策

本文采用基于信息熵确立权重的TOPSIS （technique for order preference by similarity to an ideal solution）法在Pareto解集中选取最优方案[18]。

第一步，计算所有非劣解的目标函数值，并进行无量纲化处理。

对非支配解进行无量纲化处理后，计算相对距离()以确定最优解。

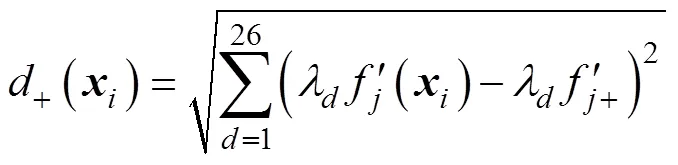
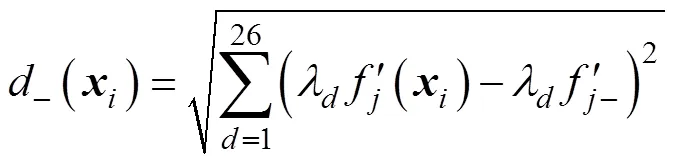
3.5 改进粒子群算法流程

本文基于MOPSO建立储能优化配置模型，流程如图4所示。

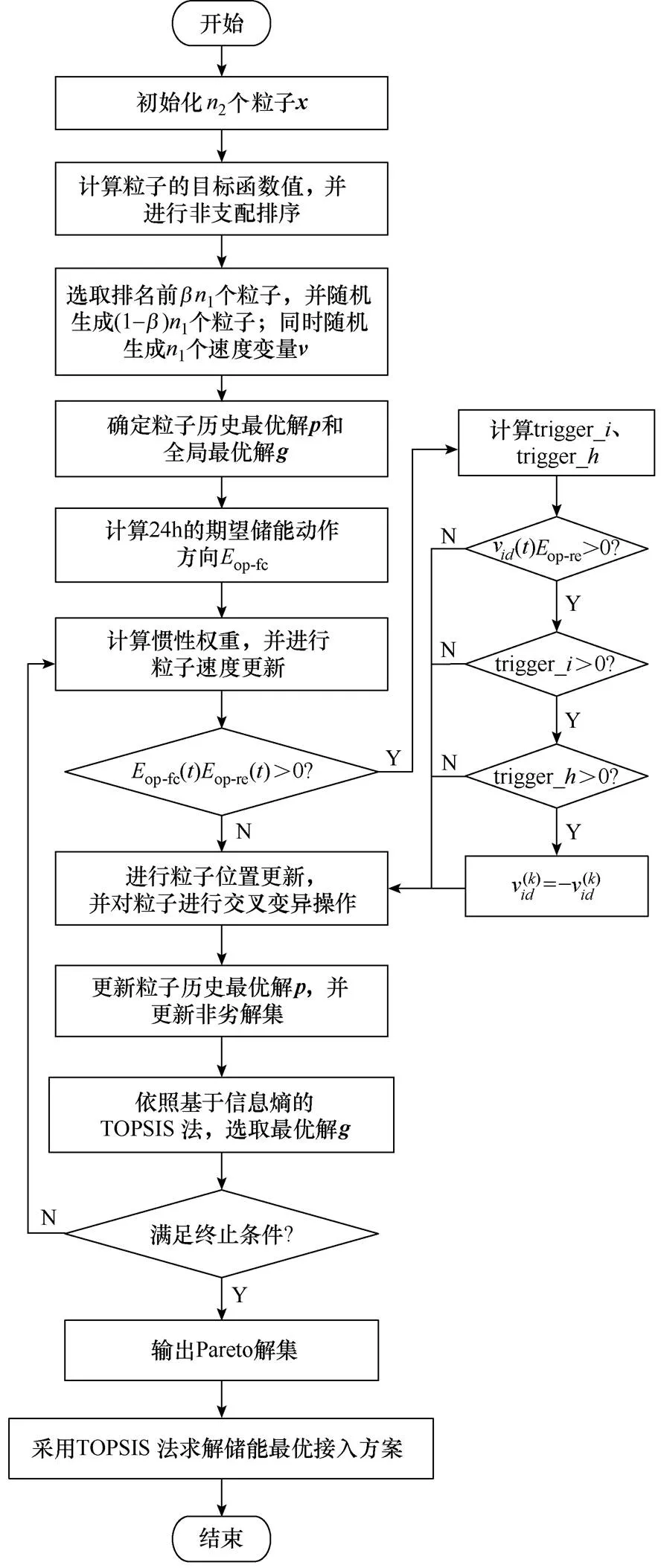
图4 改进多目标粒子群算法流程

1）设置粒子群算法参数，导入新能源、储能及系统参数。

2）初始化2个决策变量，步骤见3.2节1）。

3）初始化历史最优解及全局最优解，步骤见3.3节。

4）根据网络信息判断期望储能动作方向，并以此来指导储能各时刻动作功率。

5）计算惯性权重，进行速度更新，更新公式如式（11）所示，并判断粒子进化方向是否需要修正，若不需要修正，则直接进行步骤7）；若需要修正，则进行步骤6）。

6）依据网络信息指导粒子进化方向，步骤见3.2节2）。

7）对粒子进行位置更新，更新公式如式（12）所示。

8）更新全局最优解及历史最优解。

9）判断是否达到最大迭代次数，若未达到最大迭代次数，则转到步骤5）；若达到最大迭代次数，则执行下一步。

10）采用TOPSIS法确立储能接入电网的最佳方案。

4 算例分析

为了验证本文所提改进算法的优越性，本文采用IEEE-33节点配电网进行仿真，并在配电网中接入分布式发电装置，IEEE-33节点配电网系统如图5所示。节点17、20为光伏发电装置，节点6、32为风力发电装置，所接分布式电源容量均为200kW。

图5 IEEE-33节点配电网系统

储能类型选为磷酸铁锂电池，设置其最大容量为450kW·h，最大充放电功率为200kW。拓扑节点编号未将平衡节点包括在内，所以储能配置位置区间设置为1～32。将储能系统总体投资成本简化为1 400元/(kW·h)，运行维护成本为总投资的3%[19]。

仿真参数见表1。初始种群个数2数量为实际参加迭代的种群数量的100倍，从中挑选出20个分散的非支配优势粒子，作为初代种群的一部分参与迭代进化。

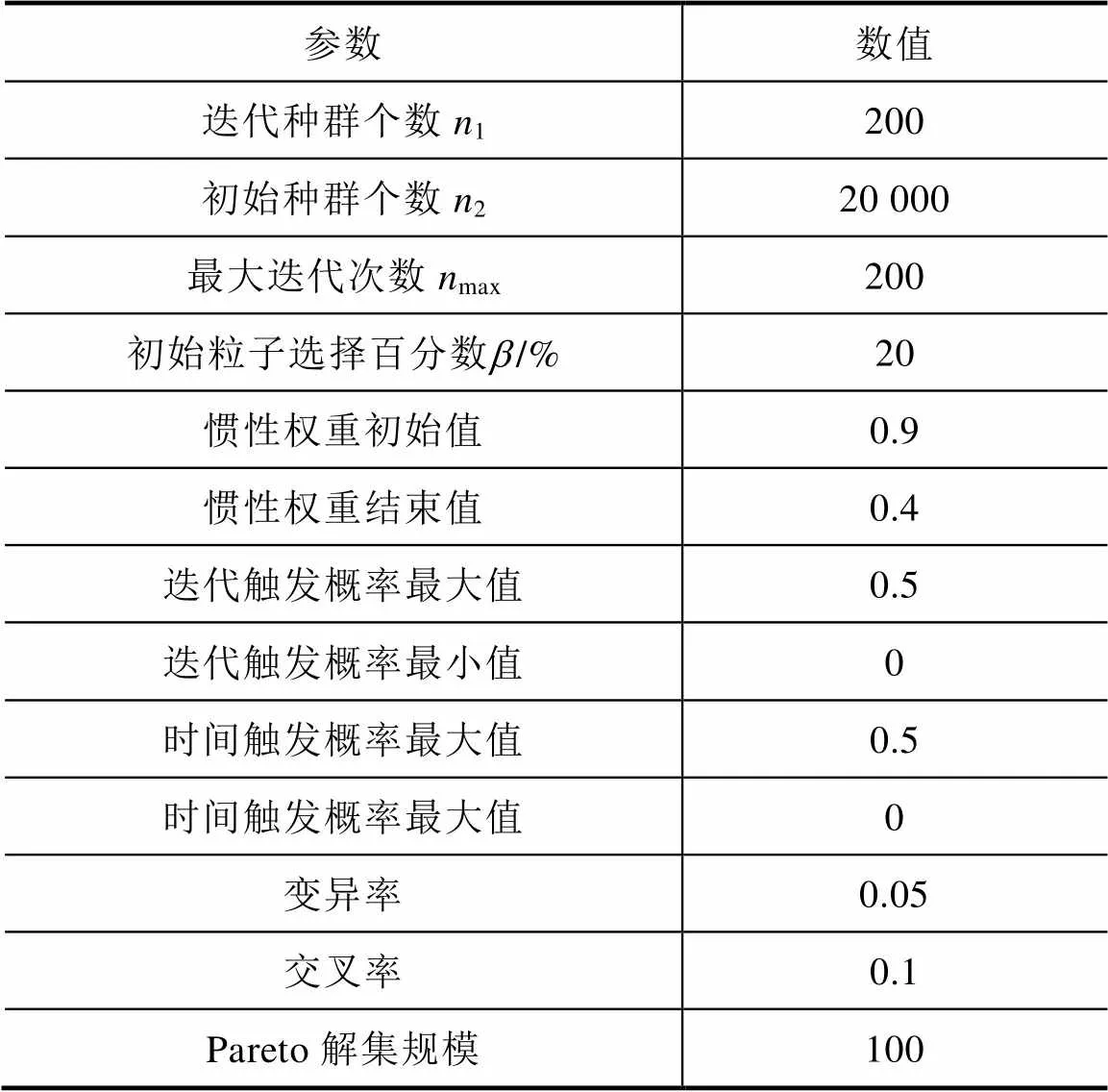
表1 仿真参数

根据本文建立的新能源出力模型，生成包含随机性的新能源出力曲线。根据式（1）生成规模为500的场景集合1，通过场景削减法得到5个场景和各自出现的概率，削减后场景如图6所示，各场景所占概率见表2。

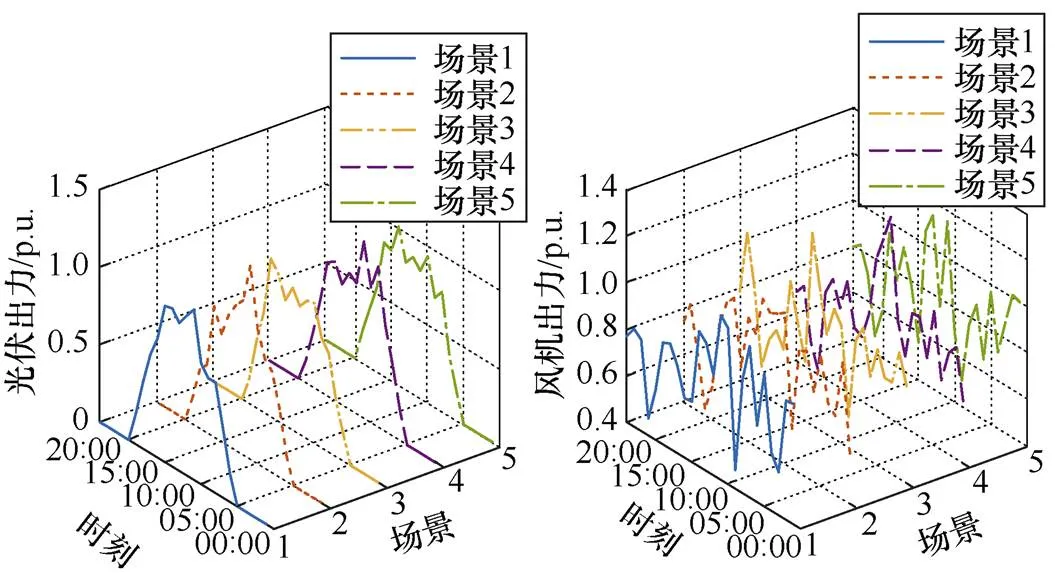
图6 削减后场景

表2 各场景概率

基于此概率将5个场景加权求和，得到等效新能源出力。风电和光伏的等效出力曲线如图7所示。

本文设置4个方案展开分析，具体如下。

方案1：不在配电网中接入分布式电源。

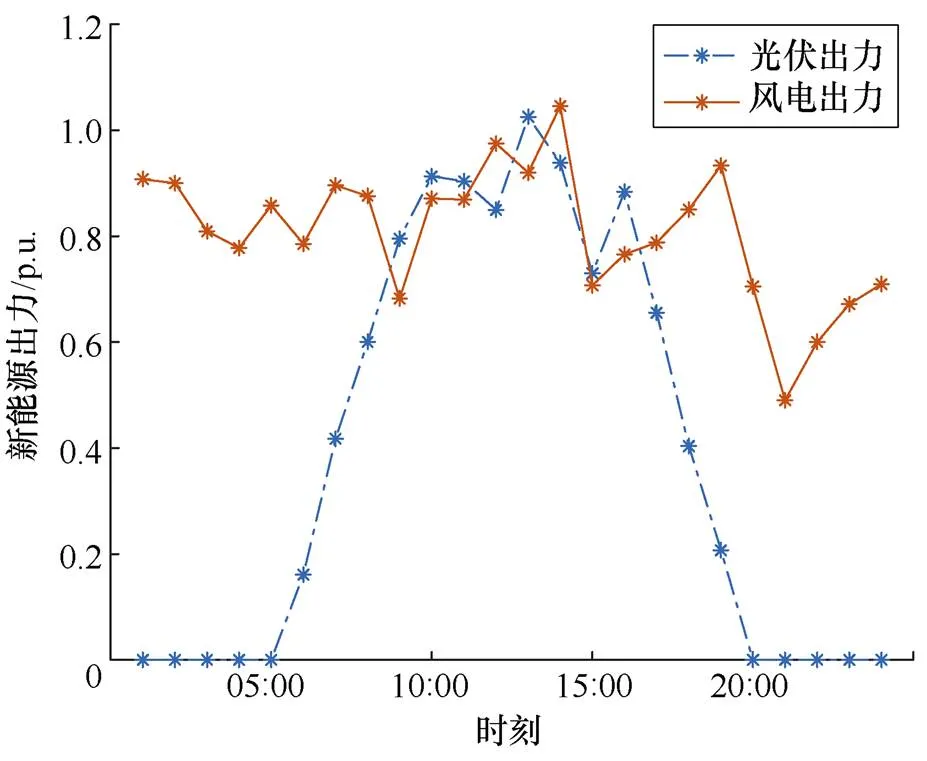
图7 新能源等效出力曲线

方案2：在配电网中接入分布式电源。

方案3：采用传统MOPSO进行储能优化配置。

方案4：采用改进MOPSO进行储能优化配置。

仿真结果见表3，各节点电压波动曲线如图8所示。对比方案1、2，在电网中接入分布式电源，分布式电源为配电网提供了功率支持，电压水平有了明显提升，而且网络损耗明显降低；但是节点电压也随着分布式电源功率的变化，出现大幅波动。对比方案2和方案3、4可以得出，储能合理的充放电动作可以降低电压波动、使网络损耗进一步降低。对比方案3、4可以得出，改进算法使各目标函数值均得到改善，表现出更好的计算精度，其中节点电压波动率降低了16.65%，网络损耗降低了4.41%。

表3 仿真结果

方案3、4计算结果中储能的配置位置均为17节点，故针对17节点电压波动曲线进行展开分析，如图9所示。图9中虚线分别表示未加储能时节点电压和节点电压平均值，对比传统算法和改进算法发现，改进算法的计算结果更贴近于节点电压平均值，表现出了更好的计算精度。

图9 17节点电压波动曲线

以上分析讨论了改进算法的计算精度，下面就算法的动态性能展开分析。为了比较算法的收敛速度和鲁棒性，本文选用Pareto解集中各目标函数的平均值，表示算法的收敛过程；选用粒子密集距离的方均根来比较算法的鲁棒性。

为了避免启发式算法的偶然性对计算结果的影响，本文统计两种算法分别独立运行20次的计算结果。计算结果的平均值与的平均值见表4。

表4 不同算法的性能比较

记录迭代过程中的Pareto解集，并计算目标函数值的平均值，收敛过程曲线如图10和图11所示。

图10 电压波动收敛过程曲线

图11 网络损耗收敛过程曲线

从表4中值可以看出，由于在粒子初始化阶段增加初始粒子数量，使Pareto解集中粒子的分散性更好，说明改进算法在迭代过程中，非劣解更加分散，局部最优的可能性更小。由图10、图11中各目标函数的收敛过程曲线可以看出，由于在速度更新阶段采用节点电压参数来指导粒子进化，使改进算法的收敛速度更快，展现了更为优越的动态性能，且改进算法收敛精度更高。

5 结论

本文针对储能优化配置问题，对MOPSO进行了改进。在粒子初始化阶段，增加初始粒子数量，通过计算密度距离挑选出分散的优势粒子，并作为初始种群的一部分参与迭代计算；在速度更新阶段，考虑解各维度之间的制约关系，采用节点电压指导速度更新过程，提高算法的计算速度；并引入trigger_、trigger_概率触发机制，减小人为干预的影响。最后通过仿真分析，对比常规MOPSO和改进MOPSO，得到以下结论：

1）在粒子初始化阶段，增加初始粒子数量，相当于增加了一次迭代计算，但是大大提升了初始种群的分散性，同时也提高了Pareto解集的分散性，使算法的稳定性更高。

2）针对储能优化配置问题，储能容量限制了储能各时刻功率的大小。此时，提高较小时刻储能动作功率的准确性，能有效提高算法的计算速度与计算精度。

3）关于指导粒子进化的系统信息还有很多，比如分时电价、新能源出力及负荷水平的大小、系统频率的高低。本文只选用了节点电压指导粒子进化，在其他配置储能的场景中，可以深入探讨不同系统信息对粒子进化过程的影响。

[1] 吴国沛, 王武, 张勇军, 等. 含光储系统的增量配电网时段解耦动态拓展无功优化[J]. 电力系统保护与控制, 2019, 47(9): 173-179.

[2] 汤杰, 李欣然, 黄际元, 等. 以净效益最大为目标的储能电池参与二次调频的容量配置方法[J]. 电工技术学报, 2019, 34(5): 963-972.

[3] 汪致洵, 林湘宁, 丁苏阳, 等. 适应于海岛独立微网的交直流混合风力发电系统及其优化调度策略[J]. 中国电机工程学报, 2018, 38(16): 4692-4704.

[4] 李建林, 李雅欣, 周喜超. 电网侧储能技术研究综述[J]. 电力建设, 2020, 41(6): 77-84.

[5] 白桦, 王正用, 李晨, 等. 面向电网侧、新能源侧及用户侧的储能容量配置方法研究[J]. 电气技术, 2021, 22(1): 8-13.

[6] 吴小刚, 刘宗歧, 田立亭, 等. 基于改进多目标粒子群算法的配电网储能选址定容[J]. 电网技术, 2014, 38(12): 3405-3411.

[7] HEMMATI R, SABOORI H, JIRDEHI M A. Stochastic planning and scheduling of energy storage systems for congestion management in electric power systems including renewable energy resources[J]. Energy, 2017, 133: 380-387.

[8] KHALID M, SAVKIN A V. Optimization and control of a distributed battery energy storage system for wind power smoothing[C]//2011 19th Mediterranean Con-ference on Control & Automation (MED), Corfu, Greece, 2011: 39-43.

[9] 张效言, 李先允. 金属加工区分层储能优化配置方法研究[J]. 电气技术, 2022, 23(1): 49-55.

[10] 李军徽, 张嘉辉, 李翠萍, 等. 参与调峰的储能系统配置方案及经济性分析[J]. 电工技术学报, 2021, 36(19): 4148-4160.

[11] 袁铁江, 张昱, 栗磊, 等. 计及功率密度约束含氢储能的预装式多元储能电站容量优化配置研究[J]. 电工技术学报, 2021, 36(3): 496-506.

[12] 肖浩, 裴玮, 杨艳红, 等. 计及电池寿命和经济运行的微电网储能容量优化[J]. 高电压技术, 2015, 41(10): 3256-3265.

[13] 吴小刚. 配网储能系统的规划方法研究[D]. 北京: 华北电力大学, 2015.

[14] 杜鹏, 彭咏龙, 黄江浩, 等. 含用户侧分布式储能的配电网降损分析[J]. 电力科学与工程, 2018, 34(8): 30-35.

[15] 陆立民, 褚国伟, 张涛, 等. 基于改进多目标粒子群算法的微电网储能优化配置[J]. 电力系统保护与控制, 2020, 48(15): 116-124.

[16] 施泉生, 王子轩, 任洪波, 等. 基于改进的模拟退火-粒子群算法的区域综合能源系统经济性运行[J]. 科学技术与工程, 2020, 20(26): 10801-10807.

[17] 董文略, 王群, 杨莉. 含风光水的虚拟电厂与配电公司协调调度模型[J]. 电力系统自动化, 2015, 39(9): 75-81.

[18] 冯喜春, 张松岩, 朱天曈, 等. 基于区间二型模糊多属性决策方法的大规模储能选型分析[J]. 高电压技术, 2021, 47(11): 4123-4133.

[19] 柴明哲, 高赐威, 陈涛, 等. 江苏省工业用户配置储能的经济性研究[J]. 电力需求侧管理, 2021, 23(3): 47-51.

Optimization configuration of energy storage based on the improved particle swarm optimization

WEN Chunxue ZHAO Tianci YU Geng WANG Peng LI Jianlin

(Frequency Conversion Technology Engineering Research Center, North China University of Technology, Beijing 100144)

Energy storage transfers power in the time dimension, which can suppress voltage fluctuations and reduce network loss. In order to reasonably configure energy storage, an energy storage optimization model is established, which is based on voltage volatility, network loss and configuration cost. The particle swarm optimization is improved by increasing the number of initial particles and selecting the scattered non-dominant particles as the initial particles to improve the randomness of the initial particles. In the speed update stage, the node voltage is used to guide the particle evolution direction and improve the calculation speed of the algorithm. Simulation results of using IEEE-33 node examples show that the improvement of the algorithm improves the stability, computational speed and accuracy. The improved energy storage configuration scheme reduces the node voltage fluctuation of the system and reduces the power loss.

distribution network; improved particle swarm optimization; energy storage con- figuration; multi-objective optimization

国家重点研发计划（2018YFB1503005）

国家自然科学基金（51777002）

2022-05-12

2022-06-17

温春雪（1980—），男，北京市人，博士，教授，从事微网运行及接口变换器控制方向的研究工作。