基于LSTM 的气味源距离估计*

闫 铮，井 涛，孟庆浩*

(1.天津大学机器人与自主系统研究所，天津 300072；2.天津市过程检测与控制重点实验室，天津 300072；3.天津大学电气自动化与信息工程学院，天津 300072)

气味源距离估计(Odor Source Proximity Estimation，OSPE)是指利用气体传感器的响应数据估计气味释放源到当前测量位置的距离。 快速、准确地估计气味源距离在气体泄漏源定位任务中具有重要意义。 近年来兴起的机器人主动嗅觉研究[1]使用移动机器人搭载气体传感器执行气味源定位(Odor Source Localization，OSL)任务；利用气体传感器信号实时估计机器人与气味源间的距离，同样有助于提高主动嗅觉的执行效率。

用于气体检测的传感器类型多种多样，其中金属氧化物半导体(Metal Oxide Semiconductor，MOS)传感器具有成本低、敏感度高且易于集成的优点，是最常用于OSL 任务的气体传感器。 MOS 传感器通过吸附被测气体改变电导率从而实现对气体浓度的检测，因此只能获取传感器所在位置较小范围内的气体浓度，且具有较长的恢复时间[2]，因此一些学者[3-10]对MOS 传感器的响应特性进行分析，综合利用MOS 传感器信号的静态/动态特征、时域/频域特征以获得实时性更高的信号处理方法，同时从中提取更丰富的信息。

基于MOS 传感器估计气味源距离的关键问题是选择合适的OSPE 指标，简称距离指标(Distance Indicator，DI)。 最直观的DI 是气味浓度:在扩散主控或者平流主控环境中，气味浓度随着气味源距离的增加而减小，这种浓度分布特点可用高斯扩散模型描述[3]。 而在湍流环境中，气味瞬时浓度分布波动强烈，明显偏离高斯分布。 为了从具有波动性、间歇性特点的信号中提取距离相关信息，研究者通常采用时间平均法，提取一段时间内信号的时均特征，以获得更稳定的DI(即时均DI)。 Ferri 等[4]通过实验证明，相对于平均浓度，MOS 传感器的响应幅值具有更稳定的距离估计效果。 Lilienthal 等[5]通过实验对比了MOS 传感器响应平均值、方差以及归一化标准差三种DI，结果表明归一化标准差用于OSPE 的精度最高。 上述时均DI 都需要对较长时间的传感器响应进行统计分析，影响了距离估计的实时性，且上述特征较为简单，OSPE 精度有限。

从频域角度看，气味烟羽信号是宽频带的随机信号，功率谱密度高达几十kHz[6]。 生物领域相关研究表明，昆虫等生物可以从复杂的气味烟羽信号中提取瞬时特征用于气味导航，以完成搜索食物或寻找配偶等活动[7]。 为获得更准确的DI，学者们开展了一系列提取MOS 传感器信号瞬时特征的研究，其中较典型的是Schmuker 等[8]通过级联滤波方法增强信号中被缓慢衰减掩盖的快速响应，即“Bout”特征，并证明Bout 个数是一种较准确的DI，即在1.45 m 范围内，该算法的平均距离估计误差为0.18 m(相对误差12.4%)。 Burgués 等[9]在Bout 特征的基础上进行改进，使用具有线性相位和有限脉冲响应的低通微分滤波器，将平均估计误差降低到0.08 m(相对误差5.5%)。 并将该算法用于无人机OSL 和气味建图研究中[10]，通过实验验证了基于Bout 特征数构建的气味分布图可以更加准确地描述气味浓度分布。

尽管传统方法已有可观成就，但设计人工特征较复杂，涉及到较多需手动调整的超参数，且一般需要持续时间较长的响应信号，影响距离估计的实时性。

MOS 传感器信号是一种典型的时间序列。 随着深度学习研究的发展，基于循环神经网络的方法在时间序列处理上取得了较好效果[11]。 相比于人工特征设计方法，深度学习方法从数据出发自动学习特征，避免了对手动参数设置的依赖，有望实现更复杂的特征表达。 长短时记忆(Long Short-Term Memory，LSTM)网络作为一种典型的循环神经网络[12]，其性能在多个时间序列处理相关领域得到了验证[13]。

本文将LSTM 网络引入OSPE 研究中，借助LSTM 网络对长序列特征的学习能力，对MOS 传感器信号进行处理，实现气味源距离的端到端估计。

深度学习研究一般需要大量数据训练网络以避免过拟合问题。 真实环境的气味扩散实验受限于复现困难、条件不可控等问题，难以大量开展重复性研究；基于计算机仿真技术实现的气味扩散仿真平台可以提供可重复的虚拟气味扩散环境，利用气味扩散仿真平台进行算法验证，已成为OSL 等研究的重要方法[14]。 本文选取广泛应用的气味扩散仿真平台GADEN[15]生成气味扩散仿真数据，对其进行LSTM 网络训练和验证。 由于环境条件(环境风场、气味源释放速率等)对气味扩散分布影响较大，为了验证模型在未知环境条件下的适应能力，本文基于不同环境条件生成仿真数据，测试网络在未知环境条件下的距离估计性能，称之为OSPE 的“环境条件泛化测试”。

本文主要贡献包括:①首次将LSTM 网络引入OSPE 研究中，利用网络自动学习DI，避免了传统估计方法对人为参数设置的依赖。 ②构建了OSPE 仿真数据集用于网络训练和参数调优。 ③通过实验对不同LSTM 网络超参数对距离估计准确性的影响进行了分析，得到了最优网络设计。 ④提出距离估计泛化测试，验证了网络对未知环境条件的泛化适应能力。

1 仿真环境数据集

气味扩散仿真为主动嗅觉研究提供了可重复的虚拟气味分布条件，已成为初期算法设计与验证的关键环节。 本文使用GADEN[15]仿真平台生成OSPE 数据集，模拟50 种环境条件(不同的气味源释放速率、气味源位置和环境风速)下的气味扩散分布，同时在仿真中设置了多个MOS 传感器用于气味浓度采样，得到了相应的气味浓度采样序列。

1.1 GADEN 仿真平台

GADEN 仿真平台基于机器人操作系统(Robot Operation System，ROS)开发，通过计算流体动力学(Computational Fluid Dynamics，CFD)软件获得环境风场数据，基于烟丝扩散模型[16]实现对气味扩散过程的仿真，从而获得气味浓度空间分布。 GADEN 根据常用MOS 传感器产品的响应特性曲线，内置了多种MOS 传感器仿真模型，本文选取TGS2620[17](Figaro公司产品)作为气体浓度采集传感器。

1.2 仿真数据集

构建了如图1 所示的室内仿真环境，环境的长、宽、高尺寸为10.4 m×6.4 m×3 m，房间设有1 个气流入口和1 个气流出口，出口设为自然压力出口。

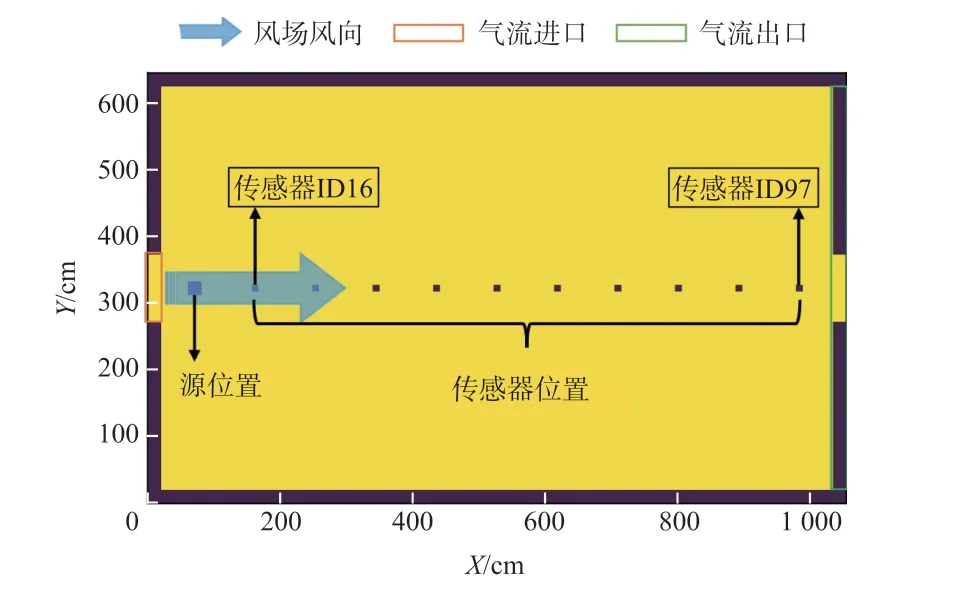
图1 室内仿真模拟环境(平面图)

入口处风向如图1 中矢量箭头所示，通过控制入口风速获得不同的环境风场。 气味源设置在空间中线(Y=300 cm，Z=150 cm)不同位置处，释放气味分子一段时间后环境内气味分布趋近稳定状态，如图2 所示。

图2 气味扩散示意图(平面图)

本文在50 种不同的环境条件下进行气味扩散仿真，即5 种不同风速、2 种不同气味源位置和5 种不同气味源释放速率，在共5×2×5=50 种组合下采集了气味扩散仿真数据。 各环境条件的取值如表1 所示。

表1 仿真环境条件

表1 中给出的气味源位置表示气味源的X 轴坐标，入口风速表示入口处的风速大小，其方向与X轴平行，气味源释放速率表示气味源每秒释放的气味分子数，即气味源浓度；本文设置的环境条件组合涵盖了常见的室内气味扩散环境条件。 针对50 种仿真环境条件组合，每种组合仿真两轮，共得到100组仿真数据。

如图1 所示，仿真气味源设置在空间中线上靠近房间入口处，104 个MOS 传感器(TGS2620，传感器ID=0 ～103，图1 中只标记出了10 个传感器)单排均匀部署在空间中线上(传感器间隔10 cm，即ID=i的传感器的X轴坐标为10×icm)进行密集的气味浓度采集。 仿真过程中采集各MOS 传感器所在位置的传感器响应和气味浓度真值(即单位空间内气味分子数，此真值由仿真平台给出)。 每次仿真获得的数据维度为(Ns×Nt)，Ns表示传感器个数(Ns=104)，Nt表示采样次数。 每次仿真从所有传感器建立稳定响应(称为有效起始时间)起采样1 000 s，采样频率为10 Hz，即每0.1 s 对传感器信号进行一次采样，即每轮仿真获得的数据集尺寸为104×10 000。

1.3 数据分析与预处理

1.3.1 有效起始时间

气味分子从气味源扩散到下风向处的传感器并建立稳定响应需要一定时间。 本文在仿真中设置一个有效起始时间，即距离气味源最远的传感器建立稳定响应所需的时间，有效起始时间后，才开始记录各传感器的响应数据。 本文分析了最小风速条件(1 m/s)和最小气味源释放速率(30 s-1)下，距气味源最远的MOS 传感器位置的浓度真值变化曲线和传感器响应曲线，据此选取有效起始时间为20 s，即仿真中气味源释放20 s 后再开始采集传感器的响应数据。

1.3.2 数据归一化

本文选取的TGS2620 气体传感器响应输出量程为[0，65 535]，仿真环境中由16 位AD 转换器采集传感器响应信号，65 535(即216-1)对应无气味响应状态，取值范围较大且分布不均匀，直接使用原始响应采样值进行训练不利于模型收敛。 因此本文采用式(1)所示的方法对数据进行归一化处理。

式中:～R表示归一化后的响应值，R表示传感器原始输出响应。 传感器响应归一化有助于加快模型训练的收敛速度和稳定性。

1.3.3 训练与测试数据集生成

一轮仿真得到的数据集记录了气味源下风向间隔为0.1 m 的密集传感器阵列的响应数据。 实际应用中难以如此密集地部署传感器；直接使用1 000 s的序列作为模型输入数据会影响应用的实时性。 因此，本文在原始仿真数据的基础上进行时间截取和空间采样(即时间和空间上的降采样)，以获得更符合实际应用场景的样本进行模型训练。

对于某一传感器的归一化响应序列(1 ×10 000)，利用滑动窗口截取不同长度的序列片段，得到时间截取后的样本(样本长度等于滑动窗口长度)。 以较大传感器间隔(间隔为0.9 cm，共选取10个传感器，)从阵列中均匀选取若干传感器(即空间采样)，得到用于模型训练的数据集。

记滑动窗口的滑动步长为S(两次截取数据时滑动窗口的移动距离)，滑动窗口长度为L，降采样后数据集样本数为100×10×{[(10 000-L)/S]+1}，其中100 为仿真次数，每个样本响应序列尺寸为1×L。

图3 为本节数据集中不同环境条件组合对应的样本数分布，不同环境条件组合的样本数分布是相对均匀的。 其中训练集和验证集样本数比例为4 ∶1。

图3 各环境条件组合的样本数量分布

2 基于人工特征的距离估计

最早用于OSPE 的指标以传感器响应序列的统计特征为基础。 Lilienthal 等[5]提出并分析了三种常用的DI 用于源距离估计的性能。 本文基于生成的OSPE 数据集对比了上述三种DI 的准确性，在训练集上对三种DI 与气味源距离的关系进行最小二乘拟合(拟合目标为多项式函数，自变量为DI，因变量为气味源距离)，基于验证集对拟合函数进行精度验证。

序列响应平均值计算公式如下:

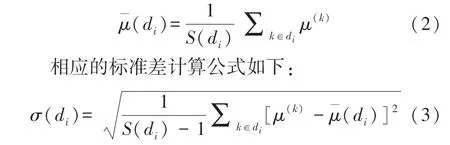
相应的平均化标准差计算公式如下:

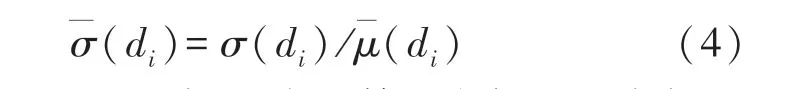
式(2)、(3)、(4)中di表示第i个气源距离标签的某一序列，S(di)表示该序列数值个数，μ(k)表示该序列中第k个数值。 按公式即可求出第i个气源距离标签下所有序列的DI用于最小二乘拟合。 拟合多项式在验证集上测试平均误差的计算公式如下:

式中:Nv表示验证集序列总数，ln表示验证集中第n个序列的距离标签，Fq表示距离指标q的拟合多项式，qn表示验证集中第n个序列的DI。

基于统计特征的DI 在验证集上的平均估计误差如表2 所示，其中平均值的距离估计效果相对较好，但是三种DI 在10m 范围内的相对估计误差都在20%以上，精度较低，难以用于实际的OSPE应用。

表2 基于统计特征的DI 验证集平均误差

3 基于LSTM 的气味源距离估计

基于统计特征的DI 计算方法简单，但距离估计精度较低。 文献[8]提出了“Bout”特征，通过设计级联滤波器，提取滤波信号中连续上升的部分作为Bout 特征；通过拟合气味源距离和Bout 特征的关系(线性函数)，获得了较好的估计效果(文献[8]给出的相对估计误差为12.4%，文献[9]改进的Bout 特征相对估计误差为5.5%)。 但人工特征涉及较多需要手动调整的参数，参数取值对估计精度影响较大，且难以考虑不同环境条件对模型参数的影响。

随着深度学习方法的发展与成熟，以循环神经网络为代表的深度网络模型在语音识别[18]、语言建模[19]和翻译[20]等时间序列处理领域中获得了比传统人工特征方法更好的效果。 针对现有基于人工特征进行OSPE 方法存在的问题，本文将深度网络模型引入OSPE 应用中，基于LSTM 网络构建距离估计模型，在大量仿真数据上进行模型训练与验证，并分析网络超参数对距离估计效果的影响。 为验证模型在未知环境条件下的距离估计效果，本文还进行了OSPE 泛化测试，通过在未知环境条件(训练时未出现过的环境条件)数据集上进行距离估计测试，验证模型的泛化能力。

3.1 LSTM 距离估计模型

LSTM 网络针对循环神经网络(Recurrent Neural Network，RNN)处理长时间序列能力不足的问题，通过设计信息选择性通过的门结构，实现对长依赖关系的学习[21]。 本文利用LSTM 网络进行MOS 传感器响应序列处理。

3.1.1 LSTM 层结构

LSTM 层结构如图4 所示。 LSTM 层包括1 个LSTM 单元，递归地处理前一层输出的序列数据。x代表输入信息，隐藏状态h和记忆状态C分别代表隐藏信息和记忆信息。

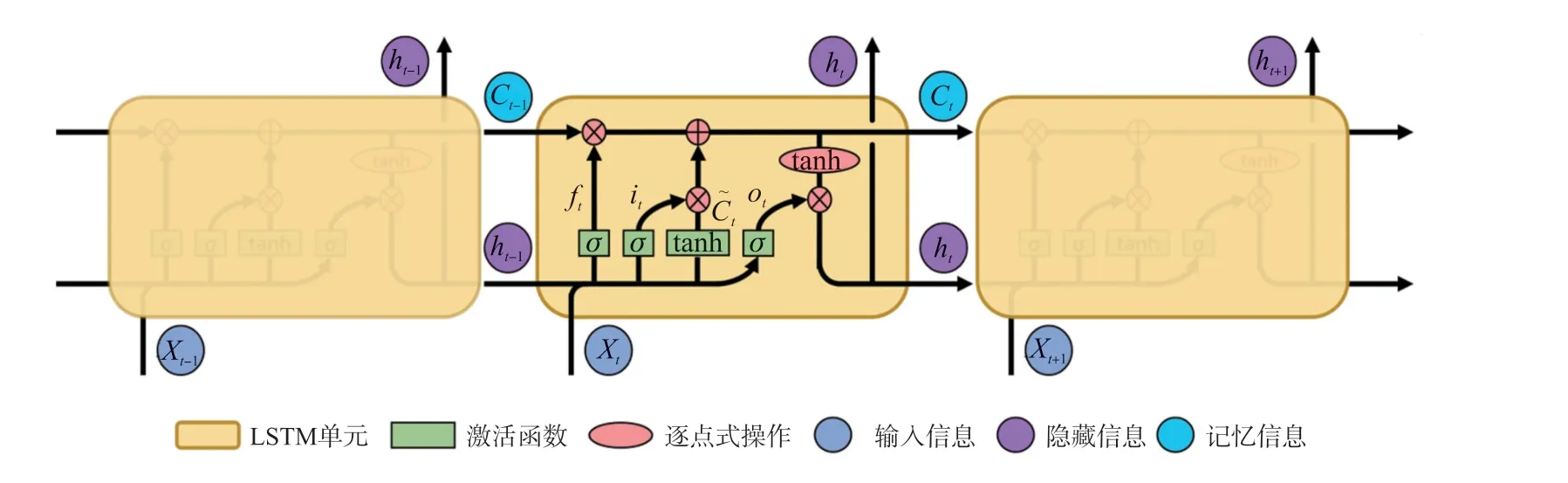
图4 LSTM 层结构

3.1.2 网络结构

LSTM 单元输入数据维度为(B，I，L)，其中B代表批尺寸(Batch size，指一次训练时并行计算的样本数)，I表示特征维度(本文特征维度固定为1)，L表示时间序列长度；单元输出数据维度为(B，H)，H表示隐藏状态h的维度。 本文选取LSTM 网络层数为W，最后一层最后一个隐藏状态作为整个LSTM结构的输出单元，输出单元接全连接网络(输入维度为H，输出维度为1)，得到最终的距离估计值，网络结构如图5 所示。

图5 LSTM 网络结构

3.2 网络训练与参数分析

3.2.1 网络训练与验证过程

分别利用PyTorch 和Paddle 实现网络构建，基于NVIDIA V100 显卡进行网络训练与测试。 实验采用1.2 节生成的仿真数据集进行网络训练和验证。 基于3.1.2 中的网络结构，以均方误差(meansquare error，MSE)作为损失函数，采用Adam 优化器进行网络优化。 为加快训练收敛速度，在训练过程中设置动态学习率，若连续10 个迭代周期内，模型在验证集上的距离估计精度提升小于0.01 m 时，则降低学习率(乘以0.5)继续训练；调整两次学习率后性能仍不提升时，结束模型训练并保存最优模型参数，训练周期设置为200。(20%)有显著降低。

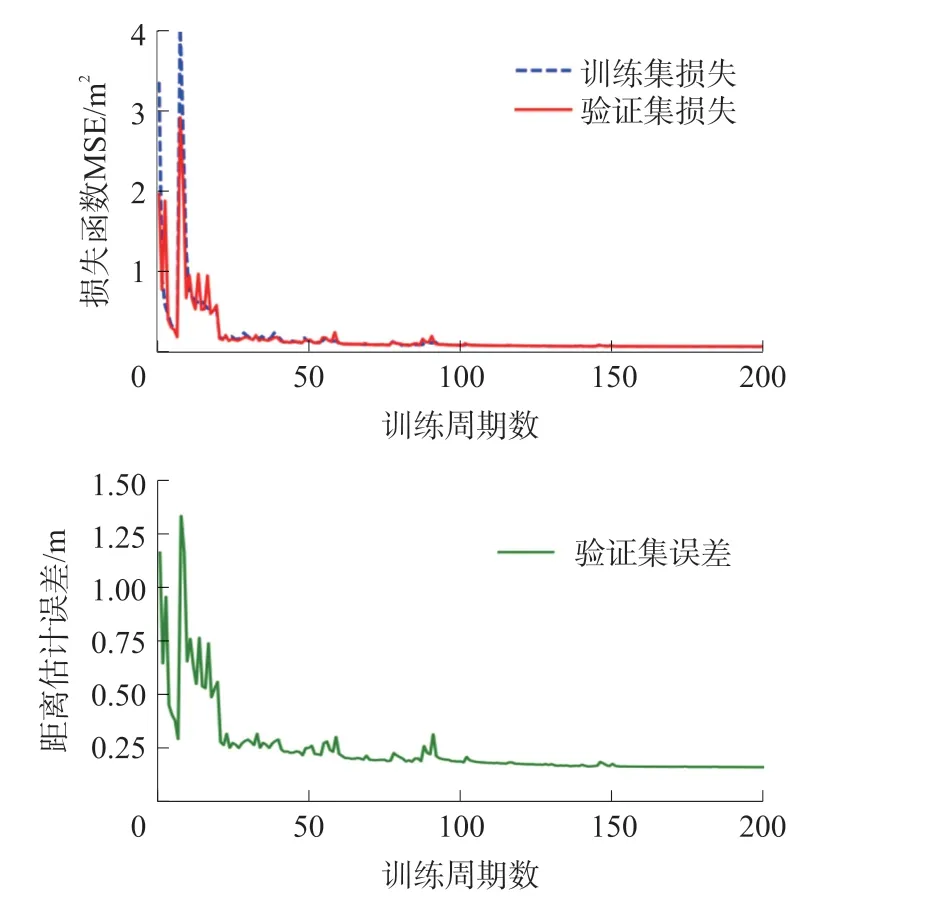
图6 最优模型性能曲线

3.2.2 超参数影响分析

LSTM 网络涉及的超参数包括LSTM 单元隐藏状态维度、LSTM 层数，以及输入步长。 上述三个超参数可能对模型性能有较明显影响，本文通过控制变量法分析不同参数对模型精度的影响。

①输入步长

分别选定如图7 中所示的8 种输入步长(采样数据长度50～2 500，对应采样时间5 s～250 s)进行验证，设置LSTM 单元隐藏状态维度为64、LSTM 层数为2，验证集距离估计误差曲线如图7 所示。

图7 不同输入步长与验证集估计误差关系

由图7 可知，当输入步长小于1 200 时，输入步长变化显著地影响模型精度，输入步长越大，有效的输入信息量越多，估计误差越小；当输入步长大于1 200 后，输入信息变得复杂和冗余，故该参数增加对模型精度几乎无提升。 充分考虑模型复杂度和精度的平衡，本文最终选定输入步长为1 200。

②LSTM 层数对模型性能的影响

增加LSTM 层数可以提高网络的特征表达能力，但会增加模型的复杂度和计算开销。 本文在验证集上对1 ～4 层LSTM 网络的模型精度进行对比(LSTM 单元隐藏状态维度为64，输入步长1 200)，验证集估计误差曲线如图8 所示。

由图8 可知，LSTM 层数设置为4 时，LSTM 网络复杂度过高，模型收敛速度较慢，开始训练90 轮后估计误差才出现明显下降。 对比其他层数，2 层的模型性能最佳，故本文选取LSTM 层数为2。

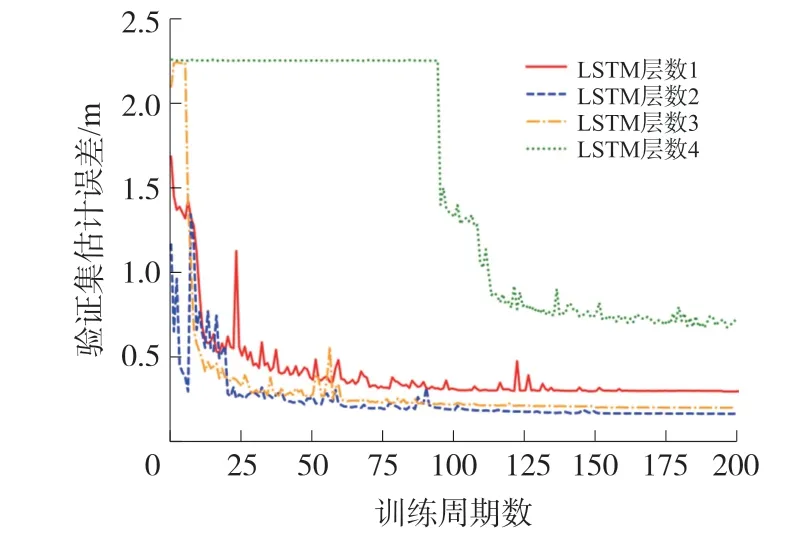
图8 不同LSTM 层数与验证集估计误差关系

③LSTM 单元隐藏状态维度

本文选取如图9 所示的5 种LSTM 单元隐藏状态维度(16 ～128)进行对比验证，设置输入步长为1 200、LSTM 层数为2，不同隐藏状态维度对应的模型验证集估计误差曲线如图9 所示。

图9 不同隐藏状态维度与验证集估计误差关系

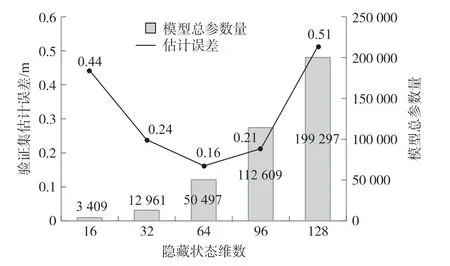
图10 验证集估计误差及模型总参数量之间关系

综上，本文选取LSTM 网络层数为2，隐藏状态维度为64，输入步长为1 200，模型训练130 轮左右趋于收敛，对应最优估计精度约为0.16 m。 网络超参数与PyTorch/Paddle 框架中的LSTM 单元参数的对应关系如表3 所示。

表3 网络参数在PyTorch/Paddle 框架中对应关系

3.3 泛化测试

3.3.1 未知环境泛化测试

模型泛化能力指模型处理新数据的能力。 由于环境条件对气味扩散分布影响较大，本文提出针对未知环境条件的泛化测试，即在基于未知环境条件生成的泛化测试数据集上测试模型的泛化能力。 首先设置与1.2 节仿真数据集生成条件完全不同的环境条件，生成新的仿真数据:设置环境风速为1.8 m/s、2.2 m/s，气味释放速率为45、55，气味源位置为X=0.75 m，基于上述条件的4 种组合生成4 组仿真数据，得到5 760 个泛化测试样本。 泛化测试集的仿真环境条件对于模型来说均是未知的(与训练集完全不同的环境条件)。

在泛化测试集上采用本文模型得到的不同气源距离区间对应的平均估计误差如图11 所示。 泛化测试集在各距离区间的样本数量分布大致均匀，整体平均泛化误差约为0.25 m，平均相对误差约为2.5%(10 m 范围)；泛化误差与距离区间有较强相关性，在距离气味源较近区域和较远区域有较高的估计精度，而在中间区域估计精度相对较低，将在后续工作中分析该情况。

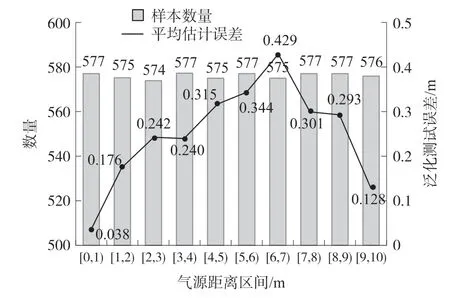
图11 不同气味源距离区间对应的泛化测试结果

3.3.2 泛化对比分析

为了验证本文基于LSTM 的OSPE 模型的有效性，将LSTM 距离估计模型与第2 章中基于三个统计DI 的拟合函数进行对比。 在相同训练集上训练模型或利用最小二乘法拟合统计指标到气味源距离的函数关系，分别在验证集和泛化测试集上测试距离估计精度。

从表4 可知LSTM 距离估计模型的验证集估计误差、泛化误差最小，较另外三种基于统计DI 的方法降低了一个数量级，泛化能力最强。

表4 不同DI 估计误差对比 单位:m

4 结论与展望

本文将深度学习方法引入气味源距离估计的应用中，基于气味扩散仿真平台GADEN 生成仿真数据集，提出了一种基于LSTM 的气味源距离估计模型，在仿真数据集上训练、验证模型，得到了较好的距离估计效果。 利用对比实验分析了LSTM 超参数对模型精度的影响，通过验证实验得到最优模型，获得了1.6%的距离估计相对误差(10 m 空间内)，显著优于基于统计指标的方法。 同时给出了模型泛化测试方法，通过生成未知环境条件下的仿真数据集对模型的泛化能力进行了验证。 本文方法利用深度学习网络特征自学习的特点，克服了传统方法对气味扩散模型和人工参数设定的依赖。

本文研究结果验证了基于深度学习进行气味源定位的可行性。 不过显然气体扩散取决于复杂众多的环境因素，例如风速、地形结构和气流障碍物等。为了进一步探讨这些因素的影响，首先还需要在更复杂自由的模拟环境中进行测试(比如在空间中添加多个气流出口或气流障碍物)，进一步完善模型和数据集(如在更多位置采集传感器响应信号)，然后思考将该方法应用于移动机器人或无线传感器网络，进一步研究主动嗅觉导航策略。