基于GM(1，1)模型隧洞不同级别围岩沉降收敛变形规律及预测

姜庆飞

(江西明泽水利建设有限公司，江西 上饶 334000)

我国水资源丰富，技术可开发总量约为4亿kW，主要集中在西南高山峡谷地带[1]。随着我国水利水电工程的蓬勃发展，越来越多的大长水工隧洞正在修建或拟建中，如40km的雅鲁藏布江大拐弯处引水隧洞[2]、98.3km的秦岭特长输水隧洞[3]、7.2km的花溪输水隧洞等[4]。由于隧洞开挖打破了岩层原始应力状态，引起应力重新分布，使隧洞围岩发生不同程度的沉降和收敛变形，造成失稳破坏。因此，在隧洞施工过程中对围岩变形进行监测，掌握隧洞的沉降与收敛变形规律，对隧洞支护时间和支护措施的选取提供决策依据，进而保障隧洞施工安全。

目前，国内外学者对隧道/隧洞的变形规律及预测做了较多研究。其中，回归分析方法在变形监测分析中使用较为广泛，包括指数型函数、对数型函数和双曲线函数等，如张俊中等采用多元回归分析对某建筑物沉降进行研究[5]，朱兴礼采用回归分析方法对富水岩溶隧道的不同变形段建立了动态分析模型[6]，夏才初等采用双曲线函数对茶林顶隧道变形数据进行回归拟合分析，并取得了较好拟合效果[7]。此外，随着灰色系统理论的不断发展，学者们逐渐将灰色理论引入隧道等变形预测中，何伟将灰色理论应用在红济石调水工程隧洞变形分析中，对比了GM、DGM和Verhulst 3种模型的预测效果[8]；夏才初采用GM(1，1)和GM(2，1)灰色模型对某隧洞水平收敛值进行分析，得出GM(1，1)模型的适用性更好[7]。然而，现有关于隧道/隧洞的变形规律及预测研究主要集中在单一地质工况，且多为隧道变形研究，对隧洞不同级别围岩段的变形规律差异缺乏探讨。因此，本文依托贵州某引水隧洞工程，对其Ⅳ级和Ⅴ级围岩典型里程段进行变形监测，分析其沉降和收敛变形规律，综合采用回归分析和灰色理论对隧洞沉降和收敛变形数据进行分析，评价2种方法的适用情况。研究结果将为隧洞的沉降和收敛变形分析及预测提供借鉴。

1 工程概况

该引水隧洞位于贵州省境内，隧洞全长8.7km，最大埋深518m，采用钻爆法施工开挖。隧洞地表属中高山地貌单元，山坡较陡，植被较发育；该区域地层结构较为复杂，揭露的地层从上至下主要有第四系全新统(Q4el+dl)粉质黏土，三叠系上统(T2)、下统(T1)灰岩、页岩，二叠系上统(P2)、下统(P1)灰岩、页岩。隧洞线路所经地区为川黔南北向构造带与北东向构造带交接的复合部位，隧洞强风化灰岩中节理裂隙较发育，呈张开-微张状。

为掌握该隧洞的变形收敛规律，对该隧洞主要里程段围岩沉降变形和收敛变形进行了监测。本文主要目的是分析不同围岩级别段的变形收敛规律，故选取了Ⅴ级和Ⅳ级典型里程段的监测数据进行分析。其中，隧洞里程段108+250～108+455围岩级别为Ⅴ级，岩体完整性：破碎-较破碎，稳定性：差-较差；里程段109+010～109+415围岩级别为Ⅳ级，岩体较完整，稳定性较好。

2 隧洞不同围岩级别段沉降收敛规律

2.1 隧洞变形监测方法

在隧洞沿线上间隔一定距离布置1个监测断面，其中Ⅴ级围岩间隔15m布置1个监测断面，Ⅳ级围岩间隔25m布置1个监测断面。隧洞沉降测点和收敛测线布置示意如图1所示，每一监测断面中布置3个测点(拱顶B点、拱肩A点和C点)监测隧洞沉降变形；在隧洞周边布置2条测线，即测试1-2和测线3-4，目的是监测隧洞的水平收敛变形。隧洞变形监测频率为每天监测1次。

图1 隧洞沉降测点和收敛测线布置示意图

2.2 隧洞沉降和收敛变形监测结果分析

本文分别选取隧洞Ⅴ级围岩和Ⅳ级围岩某一断面的监测数据进行分析。Ⅴ级和Ⅳ级围岩的拱顶(拱肩)沉降和周边水平收敛监测结果如图2—3所示。由图可知，对于2种级别的隧洞围岩，隧洞累积沉降值均随时间呈先快速增加后缓慢增长趋势；在监测初期隧洞沉降速率快，在前5d内几乎完成了累积沉降值的50%以上，沉降速率达到了1.34～2.06mm/d(Ⅴ级围岩)和0.74～1.10mm/d(Ⅳ级围岩)；在监测时间为1个月时，隧洞沉降趋于稳定。此外，拱顶的沉降明显高于拱肩，测点A和测点C的沉降值较为接近，主要是因为2测点为对称分布。隧洞累积水平收敛值随时间的增加而增加，但收敛变形速率逐渐降低，整体上比沉降值的变化更为缓慢。测线1-2的收敛值略高于测线3-4，差别不明显，Ⅴ级和Ⅳ级围岩2条测线的收敛值差异均小于1mm。对隧洞不同级别围岩而言，Ⅴ级围岩的沉降量和收敛量均大于Ⅳ级围岩，隧洞拱顶和拱肩趋于稳定时的沉降值分别为18.2mm和14.6mm、8.4mm和6.2mm。此外，Ⅴ级围岩拱顶和拱肩的沉降变形差异、以及2条测试的收敛变形差异均更大，主要原因是由于隧洞Ⅳ级围岩段岩石的完整性和稳定性均更好，在开挖之后，隧洞整体上变形更小，故体现出不同位置的沉降和收敛变形差异小。

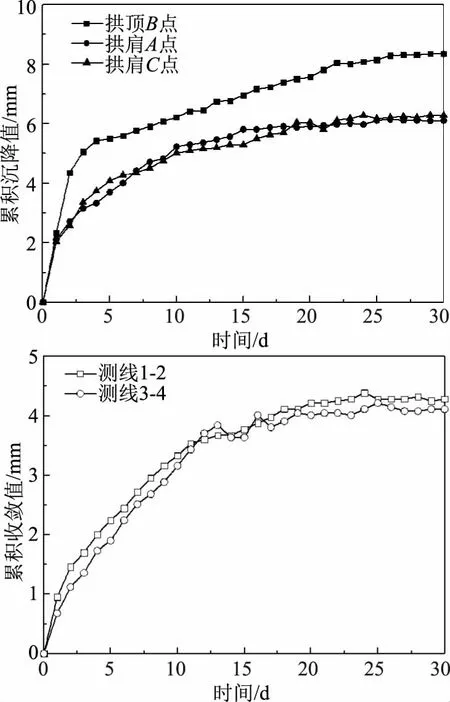
图2 隧洞Ⅴ级围岩沉降和收敛值随时间的变化曲线

3 隧洞不同围岩级别段变形预测

基于隧洞变形现场监测数据，对隧洞沉降及收敛变形规律进行理论分析，找出适用该工程地质条件下隧洞沉降和收敛变形规律的描述理论，进而对隧洞该断面或临近断面的沉降值和水平收敛值进行预测，从而能准确掌握隧洞围岩的变形趋势和稳定状态，为后续支护时间和支护措施的选取提供理论保障。

图3 隧洞Ⅳ级围岩沉降和收敛值随时间的变化曲线

3.1 基于回归分析理论的隧洞变形预测

回归分析方法是现有隧道沉降变形分析及预测的常用方法，通过对大量的变形监测数据进行回归分析，基于统计学理论建立自变量(多为时间)与因变量(如沉降值等)的拟合关系。根据建立的回归拟合函数，可对不同时刻的隧道变形值进行计算，预测隧道的最终沉降值。根据现有研究表明，隧道变形值与监测时间的拟合关系一般为非线性关系。因此，本文借鉴隧道变形预测中所采用的回归分析理论，对该引水隧洞的沉降变形和收敛变形进行分析。根据对隧洞变形数据进行初步分析，变形值与时间为非线性关系，故分别采用对数函数和指数函数对监测数据进行拟合分析，发现该隧洞的沉降变形和收敛变形均更符合指数函数关系，其具体关系式如下：

S=A·(1-e-B·t)

(1)

式中，S—隧洞累积沉降或累积水平收敛变形值；t—监测时间；A和B—拟合回归系数，与隧洞围岩性质相关。

第2节分析发现，拱肩测点A和测点C的沉降值较为接近，且测线1-2和测线3-4的水平收敛值差异也较小，因此本节只对测点A和测线1-2的变形数据进行了分析。隧洞Ⅴ级围岩和Ⅳ级围岩变形数据的回归拟合结果见表1。对于隧洞不同围岩级别，其拱顶和拱肩的沉降量、水平收敛量的拟合相关系数均大于0.9，表明拟合程度好，可采用指数函数对该隧洞的沉降和收敛变形进行预测分析。此外，根据拟合结果可以看出，拟合系数A和B分别随隧洞围岩级别的增高而增大和降低，对拱顶沉降变形和水平收敛变形而言，与Ⅳ级围岩相比，Ⅴ级围岩的拟合系数A提高了131%和128%，系数B降低了34%和35%。结合监测数据变化趋势可知，系数A代表着隧洞的最终变形值，A值越大，隧洞最终变形也越大；系数B代表曲线趋于稳定时的变化速率，B值越大，隧洞变形值越早趋于稳定。

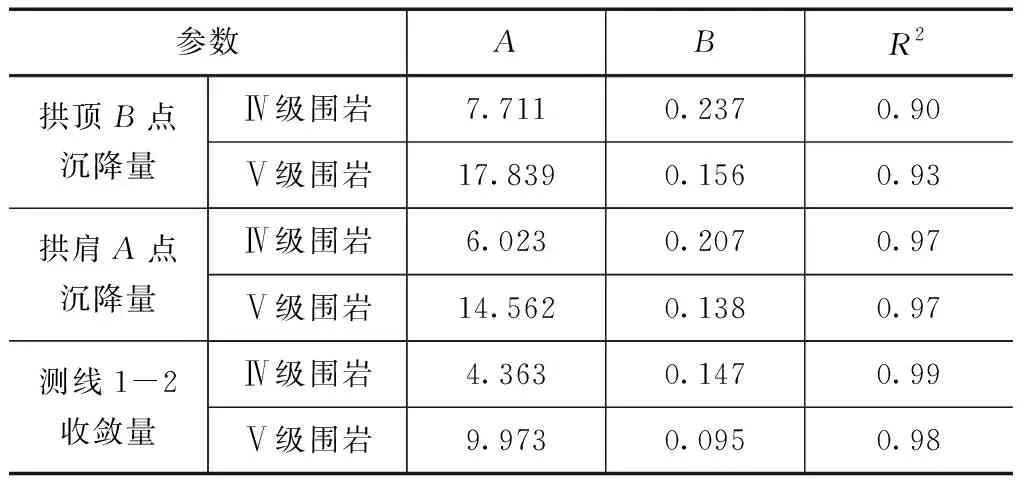
表1 隧洞不同级别围岩段变形值的回归拟合参数

3.2 基于灰色理论的隧洞变形预测

随着灰色系统理论的不断发展，学者们将其引入到隧道、路基等沉降变形分析及预测中[13]。灰色理论的主要思想是以“部分信息已知，部分信息未知”的小样本、“贫信息”的不确定系统为研究对象，通过对已有信息进行分析，从而把握系统的规律。基于现有学者的研究结果发现，灰色理论中GM(1，1)模型的适用性最好[12]，因此本文采用GM(1，1)模型对该隧洞变形数据进行分析。

隧洞在第i天的变形值及其累积变形值分别为x(0)(i)和x(1)(i)，因此可以得出隧道在不同监测时间的变形值序列：

X(0)={x(0)(1)，x(0)(2)，x(0)(3)，…，x(0)(n)}

(2)

X(1)={x(1)(1)，x(1)(2)，x(1)(3)，…，x(1)(n)}

(3)

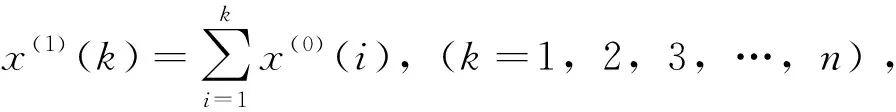
(4)

式中，a和b—模型参数，通过根据最小二乘法方法获得，具体计算如下：

A=[ab]T=(BTB)-1BTYn

(5)

式中，A—参数序列。矩阵B和Yn分别定义为：

(6)

通过求解微分方程(4)，结合初始条件x(1)(1)=x(0)(1)，可获得GM(1，1)模型的解x(1)(t)：

(7)

基于上式，可获得隧洞变形数据的响应序列x(1)(k+1)：

(8)

对于上述预测模型，采用平均相对误差Δ进行评价其预测精度，其计算公式为：

(9)

根据隧洞变形监测数据，带入式(6)可计算出矩阵B和Yn，在结合矩阵运算公式(5)可获得GM(1，1)模型参数a和b，最后带入式(8)可获得不同时刻隧洞的变形预测值。根据上述计算原理，带入该隧洞拱顶B点和拱肩A点的沉降监测数据，以及测线1-2的收敛数据，可计算出该隧洞Ⅴ级围岩和Ⅳ级围岩的沉降和收敛变形值的GM(1，1)预测模型，模型参数见表2。模型预测的相对误差大部分均小于0.05，预测精度为二级，说明预测效果较好。此外，从GM(1，1)预测模型参数可以看出，系数a和b分别随隧洞围岩级别的增高而降低和增大，致使b/a值随围岩级别的增高而增大；对拱顶沉降变形和水平收敛变形而言，Ⅴ级围岩的b/a值相比Ⅳ级围岩分别提高了133%和124%。根据隧洞变形监测数据的响应序列(式(8))，b/a值代表着隧洞的最终变形值，b/a值越大，隧洞最终变形也越大。

表2 隧洞不同级别围岩段变形值的灰色理论有关参数

3.3 隧洞变形预测模型评价

根据3.1节和3.2节中对隧洞变形监测数据进行回归拟合和GM(1，1)灰色模型分析，获得了隧洞不同级别围岩段的沉降和收敛变形值的预测模型，将指数函数拟合曲线和GM(1，1)预测模型曲线绘制在同一图中，并和实际变形监测数据进行对比分析。图4—7给出了隧洞Ⅴ级围岩和Ⅳ级围岩拱顶/拱肩的沉降变形值和收敛变形值的预测曲线。总体上而言，指数型拟合曲线和GM(1，1)预测曲线较为接近，且靠近隧洞实际变形监测值，表明2种方法均能较好的对该隧洞的沉降和收敛变形进行预测分析。然而，2种分析预测方法间也存在一定的差异，相比指数型回归预测曲线，GM(1，1)预测曲线更为靠近实际监测点，尤其是在隧洞沉降变形预测分析中(如图4和图6)，表明在现有监测数据体量下，采用灰色理论对隧洞沉降变形分析及预测的精度更高，更能反映该隧洞的沉降变形；而在隧洞水平收敛预测方面，2种方法预测精度差别不大。此外，从2种方法的理论曲线的变化趋势可以看出，Ⅳ级围岩的沉降变形和收敛变形相比Ⅴ级围岩更早趋于稳定，Ⅴ级围岩发生较大沉降变形和收敛变形的时间持续更长。

图4 隧洞Ⅴ级围岩沉降变形的预测曲线

图5 隧洞Ⅴ级围岩收敛变形的预测曲线

图6 隧洞Ⅳ级围岩沉降变形的预测曲线

图7 隧洞Ⅳ级围岩收敛变形的预测曲线

基于3.1节和3.2节中所建立的隧洞变形数据的指数回归模型和GM(1，1)灰色模型，可以对后续不同时刻的沉降及收敛变形值进行预测。基于指数函数模型和GM(1，1)模型的隧洞最终变形预测值见表3，首先利用2种理论对30d的累积沉降值和水平收敛值进行预测，并与30d的实际变形监测值进行对比分析，发现2种理论的相对误差均小于8%，且绝大部分的预测值误差小于3%，再次表明2种理论对该隧洞变形值预测的可行性和准确性。另外，观察到GM(1，1)灰色模型的预测误差整体上相比指数回归模型更低。利用2种理论对隧洞的最终变形值进行预测，对拱顶B点沉降而言，指数回归模型和GM(1，1)灰色模型的预测值分别为7.71mm和7.89mm(Ⅴ级围岩)、17.84mm和18.44mm(Ⅳ级围岩)；测线1-2最终水平收敛值分别为4.36mm和4.43mm(Ⅴ级围岩)、9.97mm和9.91mm(Ⅳ级围岩)。总体上，2种理论预测值差别较小，但GM(1，1)灰色模型的预测值稍大，更加保守。综上所述，对于该隧洞而言，采用GM(1，1)灰色模型对隧洞沉降及收敛变形预测更为精确。

表3 基于指数函数模型和GM(1，1)模型的隧洞最终变形预测值

4 结论

本文对比分析了某隧洞不同级别围岩段拱顶/拱肩沉降和水平收敛的变化规律，并引入回归分析理论和灰色系统理论对变形数据进行拟合分析和评价，预测了隧洞最终变形值。主要结论如下：

(1)隧洞Ⅴ级和Ⅳ级围岩的拱顶-拱肩沉降值均随时间呈先快速增加后缓慢增长趋势，且拱顶沉降大于拱肩、V级围岩沉降大于Ⅳ级围岩。

(2)指数型函数和GM(1，1)模型均能较好地描述该隧洞沉降及收敛变形，但较小体量的监测数据使GM(1，1)模型预测精度更高，Ⅳ级和Ⅴ级围岩的最终沉降值和收敛值分别为7.89mm和4.43mm、18.44mm和9.91mm。

研究成果对类似隧洞沉降收敛变形分析、预测和控制等具有重要意义，但没有综合考虑开挖等施工因素的影响。