基于扬压力监测的混凝土坝结构评估

韩 记

(阜阳市颍泉水利建筑有限公司，安徽 阜阳 236000)

1 概述

我国已有各种大坝18600多座，其中100m以上的14座均为混凝土坝[1- 2]。我国大坝大多建于20世纪50—70年代，近些年来新建大坝较少，老化逐渐成为我国混凝土坝面临的重要病害问题之一[3- 5]，因此延长现有混凝土坝的使用寿命或更换方案成为当前水利工程管理中亟待解决的一项重要课题。大坝建设必须满足行业指南和大坝安全法规规定的要求[6]，并且需要相关人员在现场持续监测其状况。目前，关于扬压力的监测多应用模型进行分析。王晓蕾等[7]在实测数据基础上建立了坝基扬压力与相关因子的逐步回归模型，结果证明建立的模型模拟程度较好。刘冬临[8]利用BP神经网络模型定量研究各因子对扬压力的影响，结果发现该模型无法对非线性系统进行模拟，预测精度难以保证。喻涵[9]利用逐步回归分析、遗传算法、模糊逻辑推理等方法对大坝统计模型进行了深入研究，发现采用遗传算法优化的模型在拟合精度和预测精度上都要优于逐步回归模型。本文利用集成自动监测大坝扬压力，大大缩短了前期获得实测数据的时间，再以混凝土坝结构监测为背景，给出了基于时域反射法(TDR)监测扬压力的实例，并将扬压力应用于基于概率模型的大坝结构评估中。

研究使用设备是TDR100脉冲发生器和SDMX50同轴多路复用器。250mV的发射脉冲上升时间≤0.3ns，脉冲长度为14μs。一般来说，脉冲发生器的主要缺点是在预定义时间间隔内对自动测量的支持有限，而TDR100在一定程度上可以实现该功能。本研究主要目标是开发软件来控制扬压力监测，并将其集成到常规的过程数据信息系统中。

2 试验方法

2.1 结构可靠性分析

常规结构设计和评估是基于总安全系数[10]，而不是基于对结构行为和荷载不确定性的理解。这些设计概念的区别在于处理不确定性的方式。在常规设计过程中，必须使用较大的安全系数来确保实际达到所需的安全水平，从而导致资源的不经济使用。分项系数法考虑了荷载的可变性，在具有较高自然变化的荷载中使用较大的安全系数，使得设计更经济。

概率模型是通过监测实际荷载和强度以及分析模型中的不确定性中获得的信息引入决策过程。这对现有结构提供了更高的利用率，因为结构的设计不再是通用的，而是特定于对象的。结构基于概率模型的评估提供了良好的决策支持，这是因为可以通过敏感性分析确定重要参数，剩余使用寿命可以表示为所需使用寿命的生存概率，而不是通过确定性分析得到是或否的答案。使用可靠性方法可以用于计算和评估现有大坝结构的稳定性。

2.2 扬压力

扬压力通常是混凝土坝的主要荷载之一。上世纪30年代，扬压力被纳入大坝设计中，但扬压力只能在有限点测量，难以进行量化，因此设计假设趋于保守。本文采用理论模型来描述扬压力分布，结合相关混凝土坝扬压力测量值，发现将灌浆帷幕和排水孔线相结合，可以有效地降低扬压力。排水是减少扬压力的最有效方法，扬压力模型通常通过减少扬压力线性变化来处理排水沟的存在。然而，排水沟对裂缝中扬压力的影响尚不清楚。而灌浆帷幕对扬压力的影响需要结合后续措施，一旦缺失，灌浆帷幕降低扬压力的效果并不显著。

目前，扬压力模型是基于岩体表现为多孔介质假设的[11]。如果岩体存在裂缝，则通常认为扬压力是均匀的，并与裂缝口处的扬压力相等。其次，研究表明裂缝内的扬压力是裂缝张开度的函数，并且沿裂缝过程带，该压力从全储层压力降至零。在无裂缝区域，扬压力从大坝上游面的源头到下游面的尾水呈线性变化。

随着水库水位的增加，扬压力呈指数变化。在不同的季节热负荷和较高的水库水位下，排水效率和相应的扬压力分布无法以任何置信度来预测。空气和水的季节性温度变化会给混凝土重力坝施加热负荷，导致结构运动转移到基础层面，造成张力的变化。总之，水库负荷和热负荷会可能导致扬压力偏离大坝设计时的预期值。荷载变化对扬压力的影响程度主要取决于坝下形成流道的岩石节理的渗透性和地基处理的类型和程度。

2.3 用于监测扬压力的TDR

TDR脉冲发生器以电压随时间变化快速上升阶跃函数的形式生成脉冲，当脉冲被传输到同轴电缆时，能量会从沿其路径的所有阻抗变化中反射出来。特定点处阻抗变化的量度是反射系数(ρ)，表示为入射阶跃(Vi)上反射脉冲的幅度(Vr)。通过序列采样建立了反射图，以每个数据点上叠加测量值来平均信号，并增加测量时间抑制噪声。

在水位应用中，传感器可以当作空气介质电缆，允许水在内部导体和屏蔽层之间的充气空间上下移动。在空气-水界面处遇到的强反射导致了反射图(如图1所示)中出现一个尖锐的负向弯曲。随着水位变化，反射图沿x轴平行移动与水位变化相等的距离。在本案例中，表观水位是通过对测量特征应用阈值方法来确定的，如图1所示。该方法具有自动化简单、避免噪声影响等优点。在分析中，阈值与x轴平行，计算线与反射图之间的交叉点被作为根据基准采样点校准的表观水位。

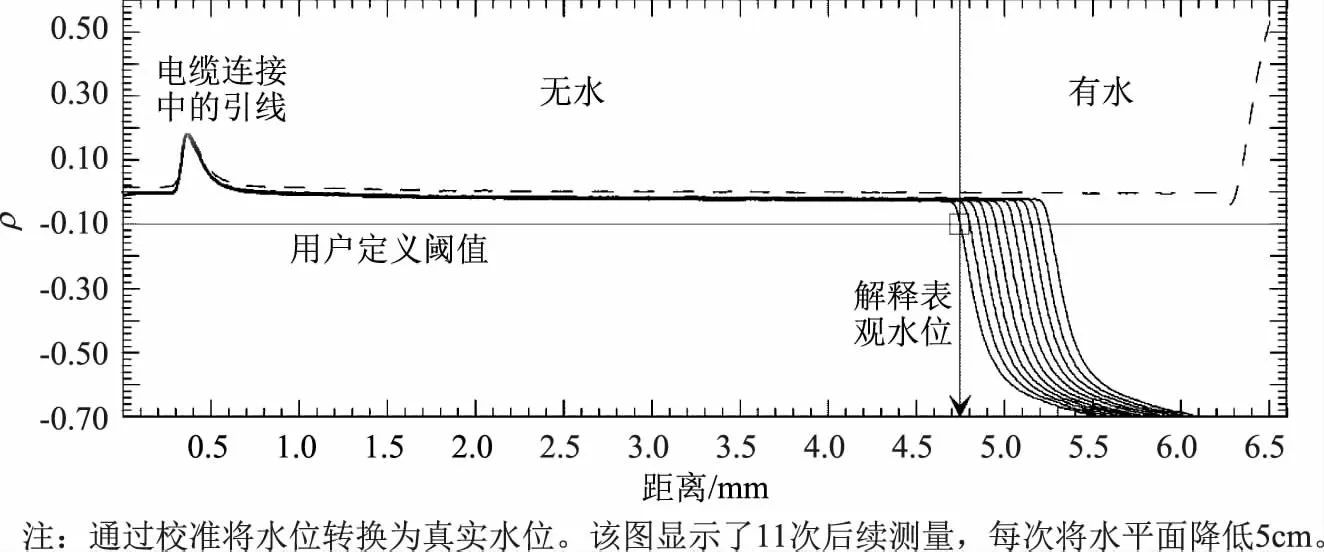
图1 根据TDR数据确定表观水位

为了评估水位传感器是否适合现场安装，并为软件开发提供信息，本文在实验室中模拟了立管中测量的扬压力。一个垂直的有机玻璃管连接到分流供水系统中，建立扬压力模拟设置。刚性21.4mm固体屏蔽空气介质同轴电缆传感器是最适合本研究的传感器。电缆的相对传播速度为0.92，从管的顶部开口端插入，并连接到TDR100。在实验中，先充水至基准面，然后升高，再降低至基准时进行TDR监测。实际水位由手动标尺读数确定。实验结果见表1。

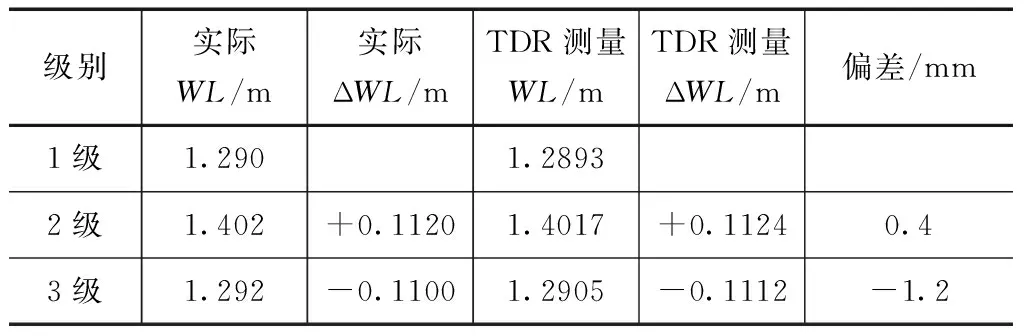
表1 实验中测量水位(WL)的结果

初始水位下的测量结果如图2所示，随后在降低水位下进行测量，然后再次升高至初始水位。每个数据集代表一个由4次重复测量叠加而成的信号，反射系数为-0.1时对应的交点处解释了试验空气-水界面反射的距离。基于112次测量下3种不同水位的变异系数(COV)≤0.0020m。将相对水位变化与标尺读数从基准面到低水位，以及从低水位回到基准面进行比较，结果差值分别为-0.4mm和+1.2mm(见表1)。实验结果表明，该方法适用于水位自动测定，精度<2mm。对于扬压力测量，这种精度是足够的。

图2 基于实验室试验的TDR数据自动解释水位的结果

3 现场试验

本案例研究位于丹江口135m长的重力坝，如图3所示，大坝建在倾斜的花岗岩表面上。在进行混凝土施工前，沿大坝上游面设置2排灌浆帷幕以降低扬压力。调查仅限于15根混凝土柱中的1根，这些混凝土柱都通过泄水闸连接。立柱的上游面高度为6.8m。

扬压力采样点是基于与混凝土结构隔离的开放式立管系统，如图3(b)所示，立管中的水仅代表地基水流量。立管有一个填沙器，从混凝土-岩石界面延伸到岩石中约0.5m。安装的塑料管起到立管(φ30mm)的作用，将取样点与潜在的混凝土水通量隔离，管材和混凝土之间的空隙被胶结。

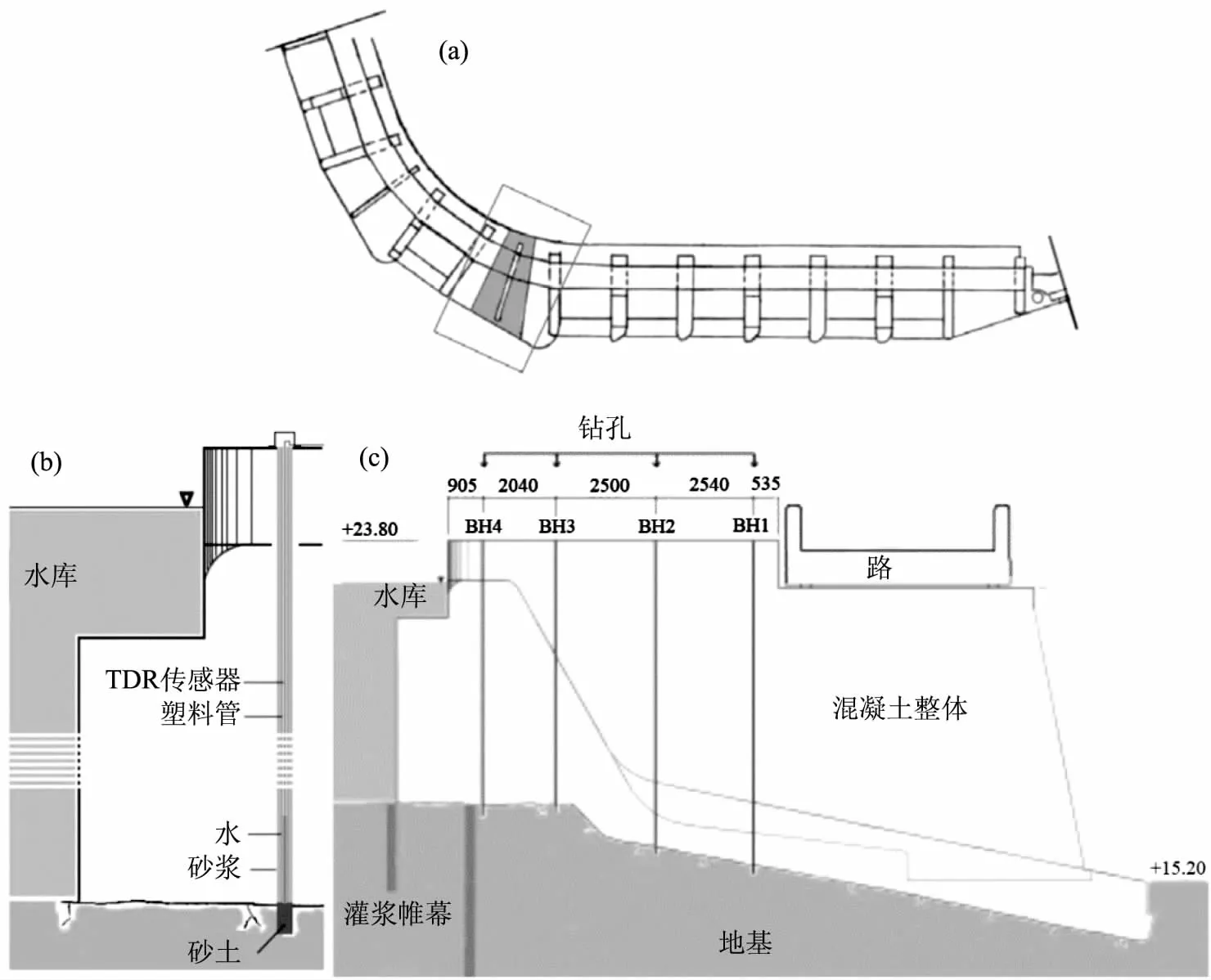
图3 (a)丹江口大坝的总图；(b)扬压力采样点的主要设计；(c)被调查柱的横截面(单位：m)

包括水库水位监测在内，调查共涉及5个采样点。最靠近立柱下游侧的点表示为BH1，其次是BH2、BH3和BH4点，BH4点靠近上游面。第5点是1根立管，直接放入到水库中并固定在柱子上。使用TDR100脉冲发生器每隔15min进行测量(在某些时间段中每30min进行1次)，立管中观测的水位代表某一时刻的扬压力。钻孔垂直于水库(沿着立柱中心线)，钻孔位置设置了2个测点，这2个测点对扬压力分布的影响最大，如图3(c)所示。当岩石表面倾斜时，钻孔深度随着与储层的距离而增加。钻孔显示整体混凝土质量较高。

利用数码相机测井，对所有4个钻孔的混凝土-岩石部分进行了成像测井。钻孔和成像测井均显示岩石破裂，这在上游最为明显。4号孔(BH4)位于灌浆帷幕附近，预计会遇到灌浆。从BH4成像测井可以看出，岩石节理受到了淋滤的影响。在地基的下游，岩石质量及其与混凝土的接触都有改善的趋势。该部分对已有裂缝仍采用水泥浆填充。测井曲线还显示，竣工柱高度与施工图纸不同，这对测量的扬压力有影响。

4 扬压力监测结果

4.1 不同横截面处的扬压力变化

前7个月的扬压力测量结果如图4所示。由于在使用TDR100时遇到的实际问题，某些时期缺乏数据。立管中测得的表观水位(以立柱顶部为基准)已根据电倾角计手动测量的结果进行校准。此后，利用钻孔和钻孔成像的数据将距离转换为水位高程，得到一个代表采样点真实扬压力的值。在图4中，扬压力也考虑了不断变化的上游水位，并以水位的百分比表示。图中未显示BH1的扬压力数据，这是由于测量的扬压力始终为零。

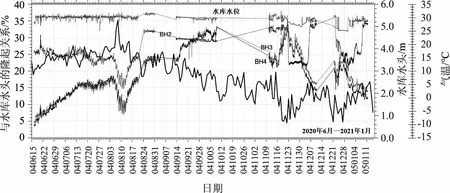
图4 7个月内BH2、BH3和BH4扬压力监测结果

考虑到标准模型假设从上游面到下游侧的扬压力呈线性下降，BH4的扬压力最高，BH3和BH2的扬压力值较低。此设置在10月的几天内是正确的，但在立柱的中心部分(BH2)发现最高扬压力时，则相反。这是因为：①沿倾斜基岩不断增加会产生额外的扬压力。②尽管帷幕深8m，但仍存在与储层接触的岩石裂缝，其影响明显受温度控制。

与BH3和BH4相比，BH2的扬压力相对稳定，BH3和BH4从6月开始出现显著的低扬压力，之后随着气温的降低，在秋季出现稳定增加。8月中旬，在高气温之后，扬压力会出现短暂的下降。在12月和1月，出现了上升波动。观测结果表明，冬季扬压力的COV随着与水库距离的增加而减小。

4.2 水库水头对扬压力的影响

通过在12:00、14:00和16:00打开溢流闸时扬压力的变化如图5所示。在每次事件之后，溢流闸门打开大约30min，水头慢慢稳定在5.4m左右。从图中可以看出，在第1个事件期间，水头下降了0.4m，且测量间隔时间越短，压力峰值可能越大。立柱中部的增幅大于其上游部分，这再次表明水库和立柱的中间部分之间存在连接，而与立柱的上游部分没有这种连接。第2个和第3个分接头处的水头下降较小，相应的扬压力变化幅度也较小。在17:00时，扬压力稳定下来。

图5 3次反复降低和增加水库水头时对扬压力的影响

在采样点之间，扬压力响应没有随时间变化的趋势，即对水库水位变化的响应在所有3个点都是即时的。扬压力数据序列之间的相关分析表明，BH3和BH4的相关系数为96%，BH2和BH4的相关系数为70%。值得注意的是，水库水位与扬压力没有很好的相关性(10～20%)，因为水头降低对扬压力有相反的影响(如图5—6所示)。在秋季和冬季，扬压力变化幅度偶尔会出现快速变化。随着气温的降低，BH3和BH4的扬压力变化稳步增加。在11月22日达到峰值的同时，BH2的扬压力突然从2m降至略低于1.5m，与这种情况相对应的是气温的上升。BH3和BH4的扬压力相对稳定地下降了近1个月，而BH2的扬压力保持不变，直到12月初再次突然跳回较高的扬压力水平。这是因为当应力状态超过阈值时，基岩中节理的温度控制开启和关闭改变了节理的水流状态。

4.3 不同扬压力分布情况

综上所述，使用目前模型估计的扬压力与现场实际测量的压力之间没有相关性。存在差异是出于安全考虑，但不适用于由于灌浆帷幕导致扬压力减少50%的假设。敏感性分析结果表明，扬压力分布对结构的安全性有很大影响。所研究的极限状态分为倾覆状态和滑动状态，并建立了极限状态方程，如下：

MR-MS<0

(1)

(2)

式中，MR—阻力，N；MS—驱动力矩，N/m；tanδg—摩擦系数；H、V—产生的水平力、垂直力，N；θ—滑动面的角度，(°)。滑动的极限状态方程直接取自我国大坝设计要求，由于粘聚力特性存在很大的不确定性，因此不考虑岩石和混凝土之间的粘聚力。

图6 11月中旬至1月中旬期间测量的水库水位和气温变化

5种不同扬压力分布情况的分析比较如图7所示。案例1：在设计中，假设扬压力呈线性递减。但花岗岩的地基不满足这一假设，因为其不是多孔介质。案例2：大坝下游地势陡倾，下游水位低于坝趾约8m。在常规设计中，很少考虑坝趾以下的水位，但此案例假定扬压力从上游水位到下游水位呈线性变化，从而导致混凝土-岩石界面的扬压力在坝下的“零点”等于零，此情况也被称为“下游水的真实位置”。案例3、4：同时考虑坝趾下游水位(3)及其实际位置(4)。案例5：分析了实际测量的扬压力。理想情况下，计算出的安全指数应基于最大年度扬压力的统计分布。由于数据集较短，每个采样点最大实测扬压力的正态分布被用作平均值，假设COV为20%。在案例1-4中假设该不确定性为对数正态分布，平均值为1，COV为0.15，见表2。在案例5(监测结果)中，预计各钻孔之间的扬压力呈线性变化。从安全的角度来看，所有钻孔会同时出现高扬压力。

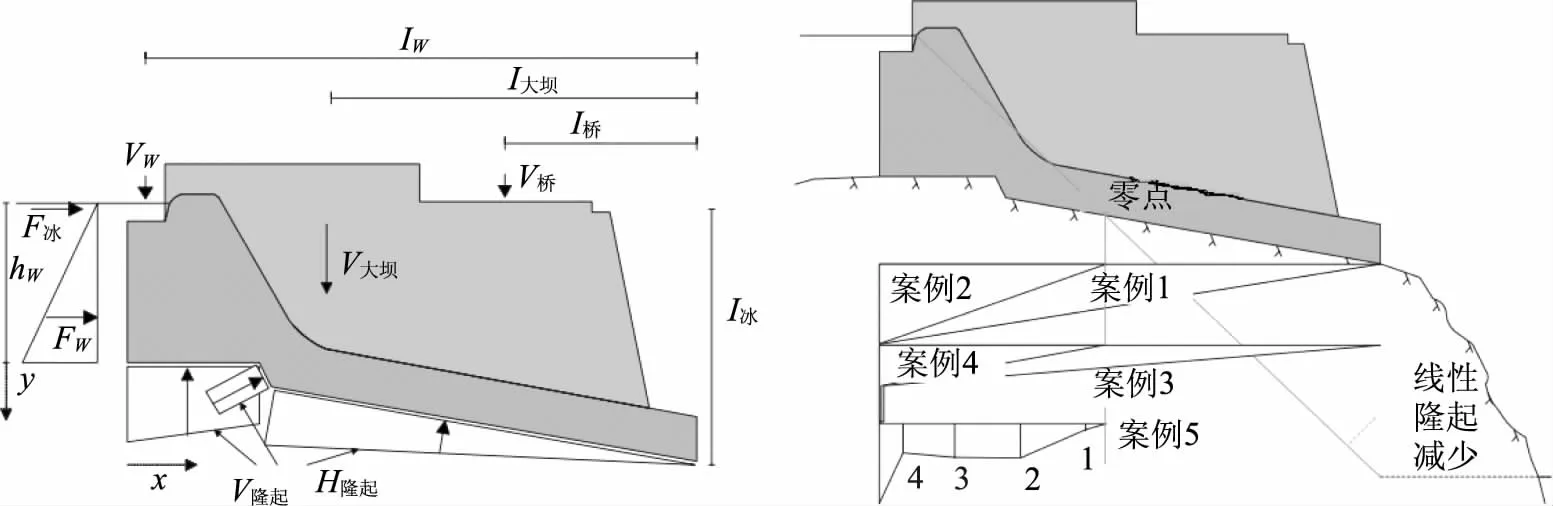
图7 (a)大坝上的作用力；(b)扬压力分布

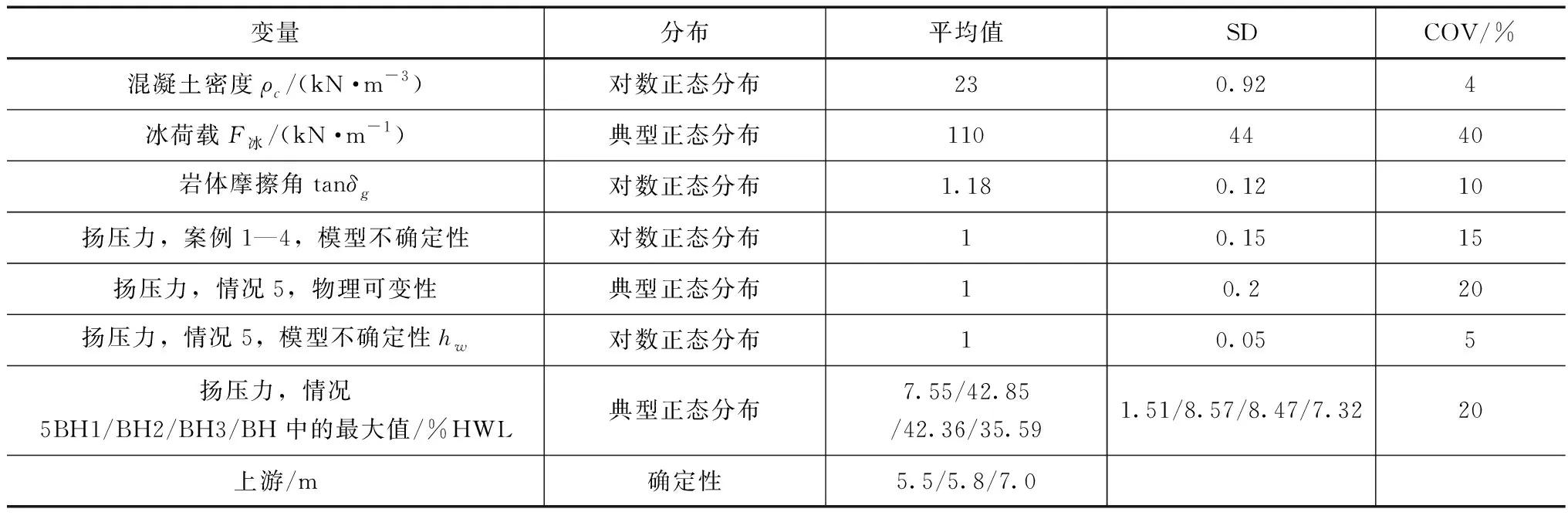
表2 可靠性分析中使用的最大实测扬压力和COV

使用一阶可靠性方法和软件计算安全指数。案例1—5在不同荷载条件下的安全指数见表3。

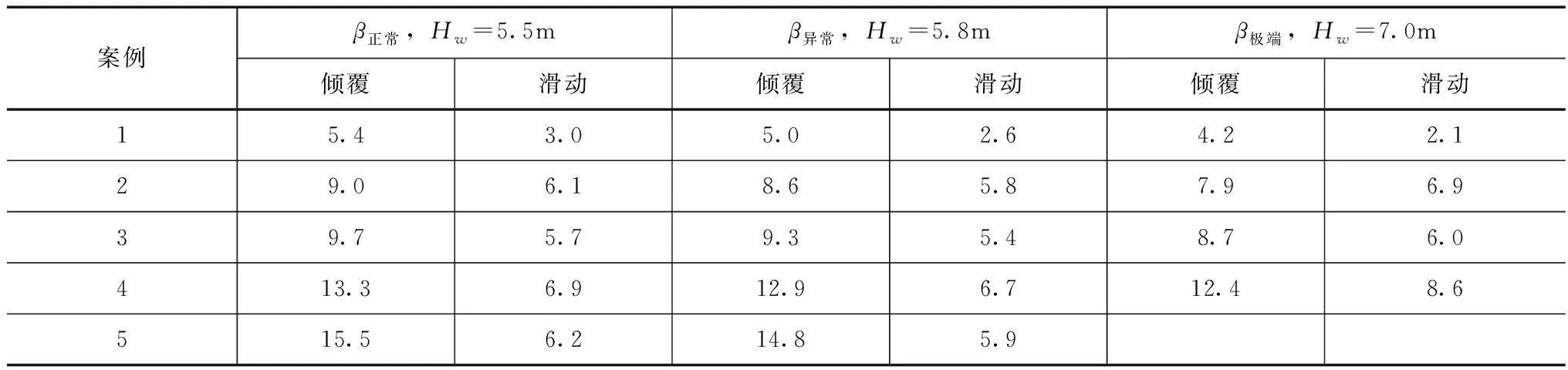
表3 安全指数计算结果

为了达到正确的目标安全指数(β目标)，还需考虑所分析案例的发生概率。1级被认为是“一直”状态。2级可能是雷雨期间发电站机组停运造成的回水，根据运行人员的说法为“每年发生几次”，因此P(2级)≈1/年。3级在20年内发生过2次，因此P(3级)≈0.1/年。因此，得到的目标安全指数为β目标，正常=4.8，β目标，异常=4.8和β目标，极端=4.25。

结果表明，与考虑实测扬压力数据的情况(案例5)相比，常规扬压力分布(案例1)严重低估了稳定性，即监测增加了有价值的信息。此外，分析表明采用常规扬压力处理的竣工立柱在倾覆方面是安全的，但在滑动方面不满足安全要求。考虑尾水位的情况下(案例2)，滑动极限状态计算结果与监测结果较为接近。但本研究结果表明，使用监测结果，该柱仍然满足要求。

显然，扬压力分布的假设对稳定性评估至关重要。为了从结构可靠性分析中获得可靠的输出，需要改进扬压力假设模型的不确定性。对于未满足设计指南稳定性要求的大坝结构，使用特定对象信息进行结构可靠性分析可以表明该结构足够安全。长期监测将提供扬压力值和扬压力变化的重要信息，在结构可靠性分析中可以正确引入该信息。这些信息减少了不确定性，也有助于发现影响稳定性的扬压力变化。

5 总结

本研究从开发自动扬压力分析软件，实验室和现场的方法论证和提升数据集在可靠性安全分析中的应用等3个方面的论证，得出以下结论：

(1)地基上的附加荷载可以在一定程度上封闭浅层裂缝系统，会导致大坝下游扬压力暂时增加。

(2)灌浆填充裂缝的最佳时期应为秋季。

(3)与实测扬压力数据相比，常规的扬压力分布严重低估了稳定性。

(4)长期监测有利于获得扬压力分布和变化的重要数据。

本文开发的基于TDR的扬压力监测，在结构可靠性分析中可正确提供大量的可用数据，为大坝工程决策提供了判断依据。但仍出现异常情况的扬压力值，无法保证完全的准确性。