基于三谐振的副边变补偿感应电能传输充电系统

钦超，杨金明，林学伟，孙杰杉，蒋志杰

(华南理工大学 电力学院，广东 广州 510641)

近年来，由于安全、方便、应用场景广等优点，感应电能传输(inductive power transfer，IPT)技术正在获得越来越多的青睐[1-4]。该技术可实现电气隔离，解决常规插拔系统诸多安全问题，已广泛应用于电动汽车、终端消费电子产品、医疗设备等领域。这些应用场景(尤其是当前“双碳”目标背景下共享电动车的广泛使用)均需要对电池进行充电。电池充电过程为：先以恒流模式充电，当电压达到阈值时转为恒压模式充电，电流降至相应的阈值时，充电过程完成[5]，如图1所示。

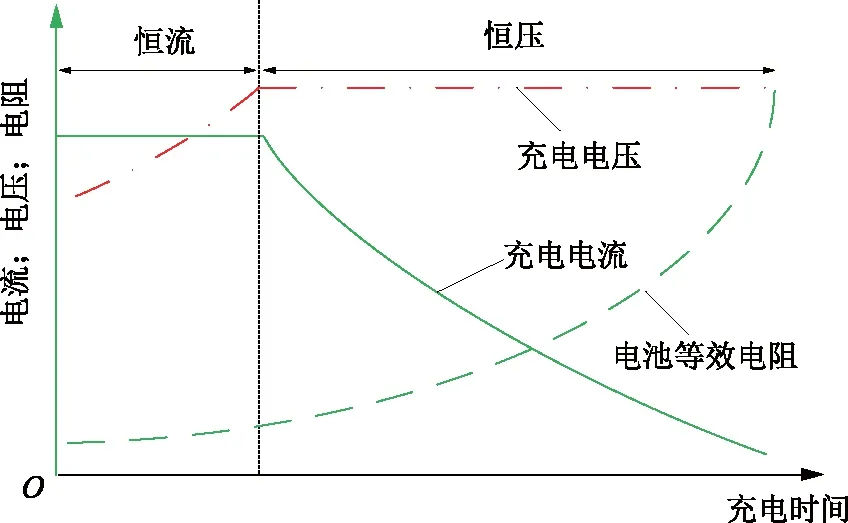
图1 典型铅酸蓄电池充电曲线

IPT系统恒流恒压充电的实现方法目前主要有2种。第一种方法是实时动态反馈控制，借助优化算法[6]或对逆变器进行变频控制[7]，可以实现恒流或恒压输出。这类控制方法增加了IPT系统的控制复杂度，有的系统可能需要原边(发射线圈)副边(接收线圈)相互通信[8]，在涉及频率调节时容易引起频率分裂现象[9-10]。第二种方法是变结构补偿，由电感器、电容器等无源元件组成恒流恒压补偿拓扑电路，在满足条件的时候借助开关进行拓扑切换，也可实现恒流恒压充电[11]。文献[12]提出在蓄电池电压上升到阈值电压时利用2个单刀双掷开关将S-P补偿切换成S-SP补偿，可以实现蓄电池的恒流恒压充电；但不能保证在恒流输出时原边电流和电压同相，且原边状态易受副边工作状态影响。文献[13-14]均提出多种恒流恒压充电副边补偿网络切换方案，并具体研究了LCC-LCC/S变结构拓扑，实现零相位角(zero-phase angle，ZPA)；但所用无源元件都较多，且副边补偿电感器在整个充电过程中都工作，不利于提高系统效率。为实现恒流恒压充电，文献[15]所提方法不仅需要调节逆变器输出频率，而且要在原边投切电容器。文献[16]提出一系列用于IPT变换器的高阶补偿电路，以满足恒流或恒压输出的要求，突破了磁耦合机构参数的约束。文献[17]提出的双LCL变补偿恒流恒压充电系统具有恒流和恒压模式下功率因数为1的特点，但所用的器件较多。文献[18]提出在输入电压恒定时,只使用1个开关切换改变原边补偿电容器从而实现副边恒流恒压切换输出的方法；但该方法需要原副边之间通信，且没有实现ZPA。文献[19]提出在副边电路增加1个开关和1个附加电容器的方法，实现对电池的恒流恒压切换充电；但恒流和恒压模式下不能同时实现ZPA。文献[20]提出在副边电路增加1个开关和1个附加电容器的方法，实现对电池的恒流恒压切换充电；但恒流和恒压模式下均不能实现ZPA。文献[21]提出在副边电路增加2个开关和1个附加电容器的方法，在实现ZPA特性的基础上对电池进行恒流恒压切换充电；但原边线圈电流易受副边电路影响。文献[22]提出在副边电路增加2个开关和1个附加电容器的方法，实现对电池的恒流恒压切换充电，充电电流可配置；但所用无源元件较多。文献[23]提出一种基于发射侧T/F变结构补偿网络的恒流恒压型感应式无线充电系统，该系统同时具备恒流恒压特性以及ZPA特性；但所用无源元件和开关器件较多。文献[24]提出的S-S/P变补偿电路所用器件较少；但逆变部分需要相移调制及变频控制，原边线圈电流不能保持恒定，充电电流不可配置。

本研究提出一种基于三谐振的副边变补偿拓扑：原边采用LCL补偿保证原边线圈电流恒定，副边采用三谐振补偿实现恒流充电，通过副边交流开关切换[21]变为S补偿，恒压模式复用了恒流模式的补偿元件。首先，分析提出拓扑的工作特性，并研究器件寄生参数对恒流恒压输出的影响，以及互感和负载变化对系统输出功率和传输效率的影响。该方法所用器件较少，充电电流可配置，输出功率的提高不受磁耦合机构参数的限制，恒流恒压充电均实现ZPA，且恒流模式充电时可在不影响恒流输出的前提下，通过调整1个电感的值来实现零电压开关(zero-voltage switch，ZVS)或零电流开关(zero-current switch，ZCS)。其次，结合工作特性推导过程，给出基于三谐振的副边变补偿拓扑的整体参数设计过程。最后，根据推导分析(下文第1章)及参数设计流程(下文第2章)设计系统参数，搭建4 A、28 V的样机进行实验，验证该方法的正确性和可行性。

1 基于三谐振的IPT充电系统分析

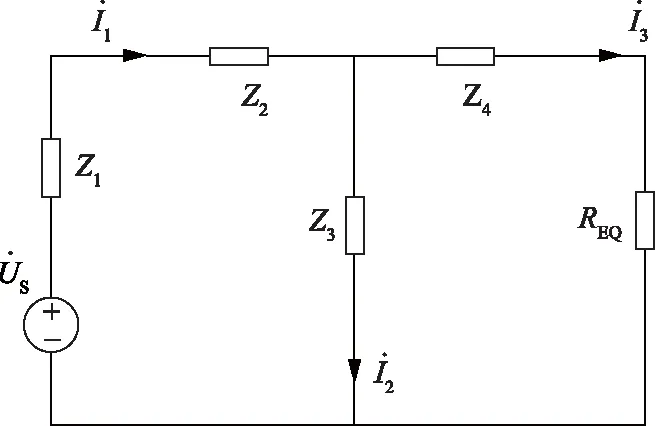
图2 IPT系统副边等效电路

a)当Z3不为无穷大(即不断路)时，由基尔霍夫电压定律和电流定律可得

(1)

当Z1、Z2、Z3满足

Z1+Z2+Z3=0

(2)

时，可得

(3)

由式(2)及Z1为感性阻抗可知，Z2、Z3至少有1个为容性阻抗。多个电感串并联时可简化为1个电感，多个电容串并联时可简化为1个电容。当3个不能再简化的储能元件各自的阻抗之和为0且达到三者共同谐振的状态时，本文定义这种状态为“三谐振”。当Z2也为感性阻抗时，Z1、Z2可简化为1个感性阻抗，此时式(2)相当于1个感性阻抗和1个容性阻抗发生谐振；当Z2为容性阻抗时，Z1、Z2、Z3实现三谐振状态。此时Z3的2种取值对应2种恒流输出电路。

b)当Z3为无穷大(即断路)时，由基尔霍夫电压定律可得

(4)

当Z1、Z2、Z4满足

Z1+Z2+Z4=0

(5)

根据以上分析，可以构造出2种副边变补偿恒流恒压IPT充电系统，分别如图3(a)、3(b)所示，即三谐振CLC/S变补偿网络和三谐振LCC/S变补偿网络，图中：UDC为逆变器的输入直流电压；Q1、Q2、Q3、Q4分别为4个增强型N沟道金属-氧化物半导体场效应晶体管(metal oxide semiconductor field effect transistor，MOSFET)构成单相全桥逆变电路；Iin为全桥逆变电路的输出电流；Uin为全桥逆变电路的输出电压；L1、C1分别为IPT系统原边补偿电感器(电感值L1)、电容器(电容值C1)，与原边线圈LP(自感值LP)一起构成原边LCL补偿拓扑；IP、IS分别为流过原边、副边线圈的电流；M为原副边线圈之间的互感；LS为副边线圈(自感值Ls)；电容器C2(电容值C2)、C3(电容值C3)与LS一起构成三谐振补偿电路；L2为补偿电感器(电感值L2)；S1为交流开关，S2为交流单刀双掷开关；Iout为由二极管D1、D2、D3、D4组成的整流桥的输入电流；Uout为整流桥的输入电压；C5为并在电池等效电阻器两端的滤波电容器(电容值C5)；T1为并在补偿电感器L2两端的双向瞬态电压抑制二极管(TVS)；RB为电池的等效电阻；UB、IB分别为整流后的充电电压、充电电流。

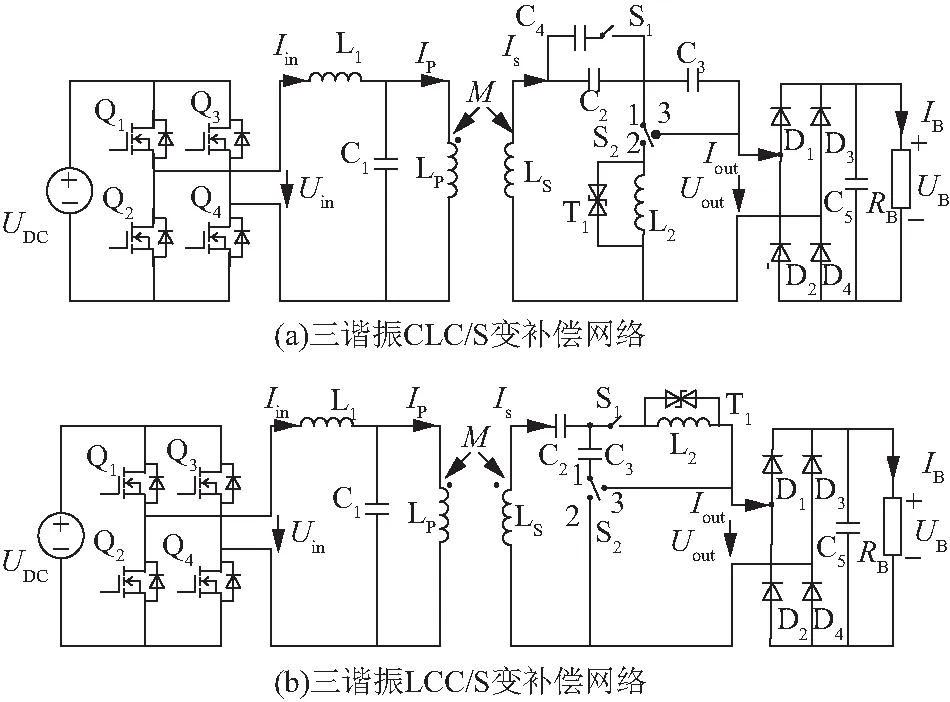
图3 基于三谐振的副边变补偿恒流恒压IPT充电系统

图3(a)所示电路用的无源元件(尤其是由多个电容通过串并联方式得到的补偿电容)数量较多，且补偿电容器C2上的电压应力较高，既提高了成本，增大了体积，又降低了可靠性；而图3(b)所示电路恒压模式复用了恒流模式的补偿元件，利用了三谐振参数约束关系，且补偿电容器C2上的电压应力较低：因此，本文选择图3(b)所示电路来实现系统恒流恒压输出。

(6)

(7)

电池等效电阻RB满足欧姆定律，即

(8)

1.1 恒流充电模式

当开关S1闭合，开关S2的“1”和“2”相连时，此时系统的拓扑为LCL-LCC结构。用受控电压源来表示原边线圈和副边线圈的互感电压[26]，可以得到系统恒流充电模式的等效电路，如图4所示，图中ω为系统的工作角频率，Req为整流桥的等效负载电阻。

图4 恒流模式系统等效电路

由基尔霍夫电压定律可得方程组

(9)

由式(7)、(8)可得

(10)

系统工作角频率ω、电感L1、原边线圈自感LP、副边线圈自感Ls、原边补偿电容C1、副边补偿电感L2、副边补偿电容C2和C3之间满足关系式(11)—(14)﹝其中式(13)即前文所述三谐振方程﹞：

(11)

(12)

(13)

(14)

为保证系统工作频率稳定，系统恒流充电工作角频率

(15)

将式(11)—(15)代入式(9)，可得流过等效负载电流

(16)

(17)

当满足式(14)条件时，式(17)可简化为

(18)

由式(16)—(18)可知，系统工作于恒流模式时，通过选择合适电感值(即副边补偿电感L2的额定值)，可以使系统的输入阻抗为纯阻性(即可以实现ZPA)，理论上没有无功功率的输入，从而将更多的能量传递到负载端，有助于提高系统效率。同时，由式(16)可知，L2的值并不影响恒流输出值，可以在一定范围内通过改变L2的值来调整系统工作于ZVS或ZCS状态。适当减小L2，输入阻抗呈弱感性，利于实现ZVS，相量图如图5(a)所示；适当增大L2，输入阻抗呈弱容性，利于实现ZCS，相量图如图5(b)所示。

图5 输入阻抗呈弱感性和弱容性相量图

由于电容采用多电容并联实现，其内阻很小，可忽略不计。当考虑电感、原边线圈和副边线圈内阻时，由基尔霍夫电压定律可得方程组

(19)

解式(19)可得，考虑器件内阻时恒流模式等效负载电流

(20)

其中：

(21)

B=jωLP+RP，

(22)

(23)

(24)

(25)

(26)

理想情况下和考虑器件内阻时4 A恒流充电电流IB随等效负载电阻Req变化曲线如图6所示。

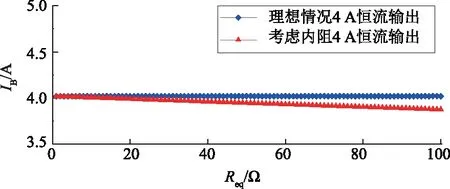
图6 理想情况、考虑内阻时4 A恒流充电电流与负载电阻关系

由图6可以看出，在考虑器件内阻情况下：当Req增大时，实际输出电流会呈现降低趋势；在Req较小时，实际恒流输出和理想恒流输出之间误差很小。在给电池恒流恒压充电的过程中，Req不断增大，这对电池的恒流充电过程是有利的。

此时系统输出功率

(27)

传输网络总损耗

(28)

系统的传输效率

(29)

系统输出功率Pout与等效负载电阻Req、耦合系数k的关系如图7所示。由图7知：k较小时，Pout等级都较低；随着k的增大，Pout等级明显提高，增大k有助于提高IPT系统的Pout等级。

图7 恒流模式下系统输出功率与负载电阻、耦合系数关系

系统传输效率η与等效负载电阻Req、耦合系数k的关系如图8所示。由图8可知：k一定时，η随着Req的增大总体上逐渐降低(这是由于考虑器件内阻时，随着Req的增大，恒流输出电流值呈减小趋势)，且k越大，随着Req的增大，η下降越快；当Req一定时，η并非随着k的增大而一直增大，且Req越大，实现η最大需要的k越小。

图8 恒流模式下系统传输效率与负载电阻、耦合系数关系

图9展示了归一化输出电流与C2、C3、L2的归一化参数之间的关系。根据图9可知：电容C3的参数对恒流输出值的影响比较明显；电容C2的参数向上或向下偏差均会使恒流输出值减小；电感L2的变化不影响恒流输出值。

图9 归一化恒流输出电流与C2、C3、L2归一化参数关系

图10展示了L2归一化参数对输入阻抗相角的影响。根据图10可知：附加电感L2取值比额定值略小时，输入阻抗呈弱感性，利于实现ZVS；取值比额定值略大时，输入阻抗呈弱容性，利于实现ZCS，便于在不影响恒流输出值的前提下实现逆变器软开关的调节。这与图5展示的结论是一致的。

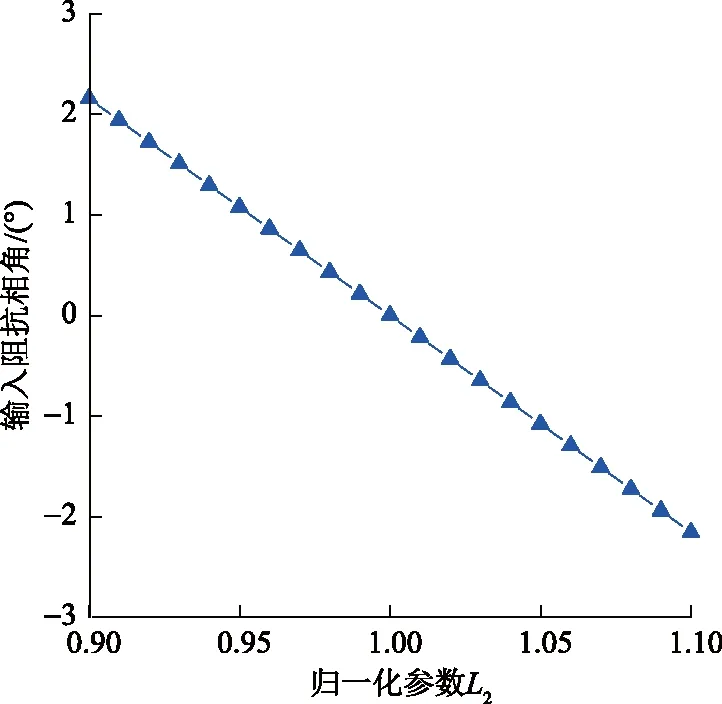
图10 输入阻抗相角与L2归一化参数关系

综上，可以在大于0.1的宽范围内选取耦合系数，以保证恒流充电较高的输出功率等级和传输效率，且最好在Req较小的时候进行恒流充电。同时，要保证副边电容C2、C3的参数偏差尽量小一点，以稳定恒流输出。

1.2 恒压充电模式

当开关S1断开，开关S2的“1”和“3”相连时，此时系统的拓扑变为LCL-S结构。根据互感等效模型，恒压充电电路可等效为图11所示的电路。

图11 恒压模式系统等效电路

图11中的C3也可以通过图12(a)、(b)、(c)3种方式组合获得，但图12(a)、(b)中的方法使得附加电容器及相应的切换开关的电流应力提高了1倍，图12(c)所示方法使得附加电容器及相应的切换开关的电压应力提高了1倍；因此，本文采取的方法相对来说有利于减少无源元件数量，同时降低部分无源元件和开关器件的电压应力和电流应力，从而在一定程度上提高系统可靠性。

图12 补偿电容C3的几种获得方式

由基尔霍夫电压定律可得方程组

(30)

其中，系统工作角频率ω、电感L1、原边线圈自感LP、副边线圈自感LS、原边补偿电容C1、副边补偿电容C2、C3之间同样满足关系式(13)、(15)，这样可以确保整个充电系统频率稳定。于是可得系统的等效负载电压

(31)

(32)

可知，恒压充电模式时的系统输入阻抗也呈纯阻性，也可实现ZPA。

当考虑电感、原边线圈和副边线圈内阻时，由基尔霍夫电压定律可得方程组

(33)

此时恒压输出

(34)

理想情况下和考虑器件内阻时28 V恒压充电电压UB随Req变化曲线如图13所示。由图13可知，考虑器件内阻时，恒压充电电压值会比理想情况下略低，尤其是在Req较小的时候。

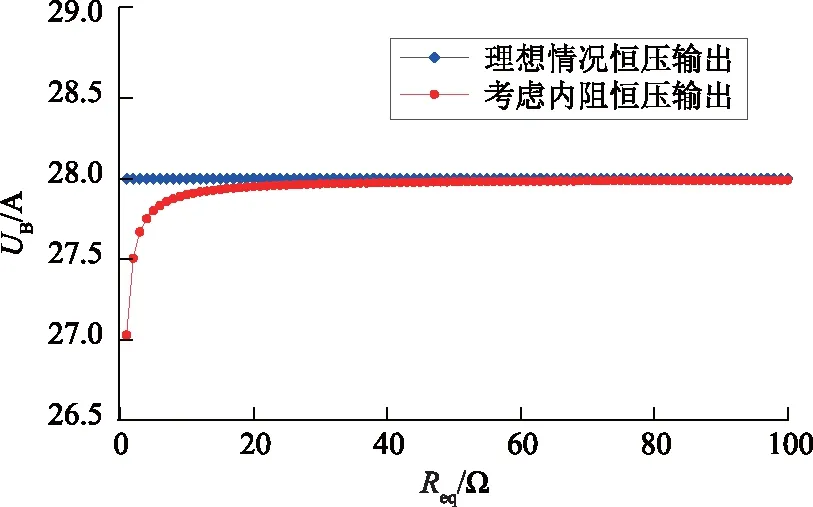
图13 理想情况、考虑内阻时28V恒压充电电压与负载电阻关系

系统输出功率Pout与等效负载电阻Req、耦合系数k的关系如图14所示，可知，恒压充电时，Pout随着Req的增加明显下降，恒压充电后期Pout较低。

图14 恒压模式下系统输出功率与负载、耦合系数关系

系统传输效率η与等效负载电阻Req、耦合系数k的关系如图15所示，可知，k较小时η较低，k大于0.1时，总体上η都很高。

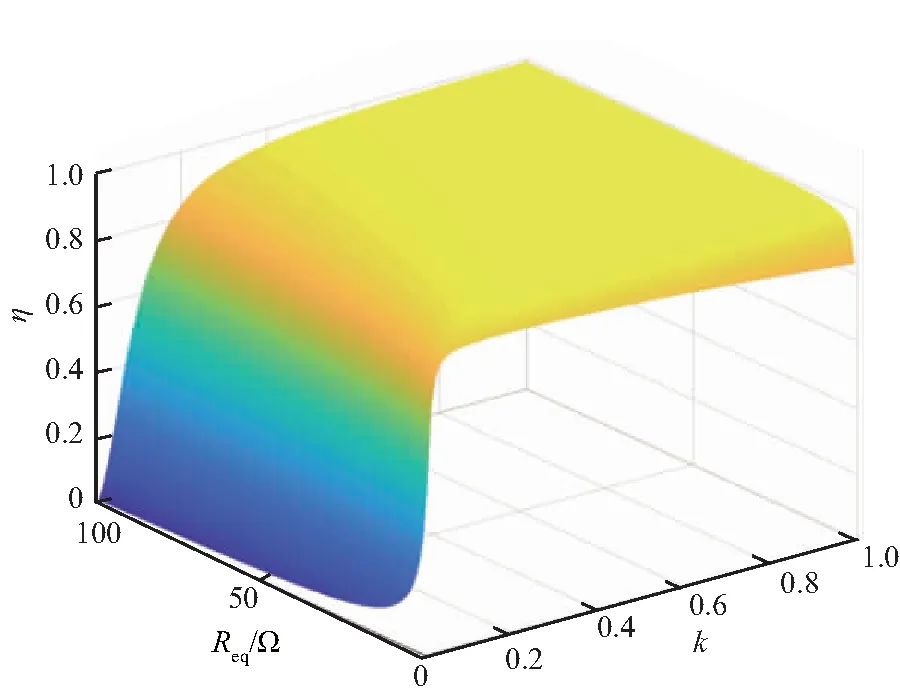
图15 恒压模式下系统传输效率与负载、耦合系数关系

2 系统参数设计

在实际应用场景中，当已知磁耦合机构参数LP、LS、M和系统频率f时，可求出角频率ω、电感L1、补偿电容C1及补偿电容C2、C3串联等效电容。此时，当已知充电电压UB时，可求出系统输入直流电压UDC及逆变器输出高频交流电压的基波有效值Uin。结合需要的充电电流IB，便可求出副边关键器件参数L2、C2、C3。

可结合实际需求，根据图5、图10来调节L2的值，来使系统实现ZPA、ZVS或ZCS。由图6和图13可知，考虑器件内阻时，恒流输出值和恒压输出值都比理想情况下略低；因此，可通过适当增大逆变器输入直流电压UDC及Uin，来适当提高和稳定恒流输出值和恒压输出值。分析充电模式可知，磁耦合机构的耦合系数可以在大于0.1的宽范围内，保证2种工作模式下实现较高的效率和较高的功率等级，本文实验设置在0.4左右。

该方法参数配置灵活，可以根据IPT系统恒流充电实际需要的恒定充电电流值，来配置补偿电容C3的大小，再据此来匹配其他相关参数，从而满足在IPT系统恒压输出值不受影响的前提下，实现多级恒流输出。该方法使得系统输出功率的提高不受磁耦合机构尺寸参数的限制。

2.1 原边参数设计

当磁耦合机构参数LP、LS和M已知时，由式(11)、(12)知，

L1=LP.

(35)

由式(11)可知，

(36)

由式(9)和式(30)可得，原边线圈恒定电流有效值

IP=ωC1Uin.

(37)

由式(37)可知，当系统工作角频率ω、原边补偿电容C1以及逆变器输出电压基波有效值Uin不变时，IPT系统原边线圈电流恒定。此时，副边复杂工作情况(尤其是不同充电电流情况)不会影响原边线圈电流。

2.2 副边参数设计

a)恒压配置。由式(1)、(2)、(31)可得UDC与UB之间关系：

(38)

当UB已知的时候，可求出参数UDC和Uin。由式(30)、(31)可得

(39)

b)恒流配置。由式(1)、(2)、(11)可得UDC与IB之间关系：

(40)

当IB、UDC已知时，由式(40)可求得参数C3，同理，由式(39)可得参数C2值。由式(14)、(40)可得参数L2值，即

(41)

式(35)—(41)给出了基于三谐振的副边变补偿恒流恒压IPT充电系统的具体参数设计方法，系统参数设计流程如图16所示。由已知的系统参数规格，按照该方法配置的IPT充电系统，可以在实现多等级恒流和恒压充电的同时实现ZPA、ZVS或ZCS。

图16 系统参数设计流程

3 实验验证

为验证所提出的基于三谐振的副边变补偿恒流恒压IPT充电系统的正确性和有效性，参照图3(b)所示系统结构搭建了图17所示简化实验样机。原副边线圈采用外径2.97 mm、截面积3.53 mm2的利兹线，原副边线圈尺寸均为10匝300 mm×300 mm，间距为35 mm，且中心轴重合，无横向和纵向偏移。实验中采用MMKP82系列谐振电容器，整流二极管型号为PFR20L45，采用ITECH公司生产的电子负载IT8513C+来模拟电池等效电阻RB的变化[19]。具体的系统电路参数：系统工作频率f=100 kHz；直流源输出电压UDC=64 V；原边补偿电容C1= 45.289 nF；原边补偿电感L1=55.93 μH；原副边线圈之间互感M=26.03 μH；原边线圈电感LP=55.93 μH；副边线圈电感LS=57.23 μH；恒流补偿电容C2= 52.553 nF；恒流补偿电容C3=280.499 nF；恒流补偿电感L2=9.03 μH；原副边线圈之间距离d=35 mm。

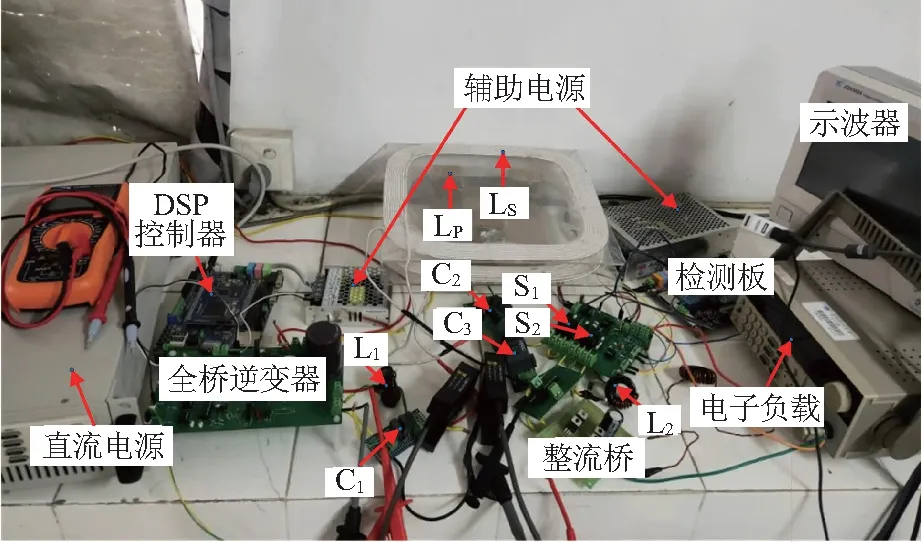
DSP—数字信号处理器，digital signal processor的缩写。

在恒流充电阶段，电池等效电阻RB由5 Ω按0.2 Ω增量依次增加到7 Ω，充电电流IB稳定在4 A左右，充电电压UB从20 V增加到28 V左右；在恒压充电阶段，RB由8 Ω变化到72 Ω，UB稳定在28 V左右，IB逐渐降低至0.4 A左右。

图18所示为恒流模式逆变器输出电压uin、输出电流iin、充电电压UB、充电电流IB的波形。图18(a)中RB=5 Ω，此时Pout=82.51 W，η=84.89%；图18(b)中RB=7 Ω，此时Pout=107.43 W，η=84.79%。这2个工况对应的IB分别为4.062 A和3.917 A，电流变化率为3.57%。图18(c)是恒流充电时RB由5 Ω突变为7 Ω的过渡过程波形。由图18知，在RB发生变化时，uin和iin几乎始终同相位，系统实现ZPA，IB基本稳定。同时，恒流充电时IB随RB的增大而降低，这与理论分析部分结论一致，验证了理论分析的正确性。

图18 恒流模式逆变器输出电压、输出电流、充电电压及充电电流波形

图19所示为恒压模式逆变器输出电压uin、输出电流iin、充电电压UB、充电电流IB的波形。图19(a)中RB=12 Ω，此时Pout=65.57 W，η=90.69%；图19(b)中RB=72 Ω，此时Pout=11.85 W，η=82.87%。这2个工况对应UB分别为28.049 V和29.223 V，电压变化率为4.19%。系统在恒压模式下UB基本保持恒定，uin和iin基本保持同相位。

图19 恒压模式逆变器输出电压、输出电流、充电电压及充电电流波形

图20所示为充电模式切换时，开关S1和S2的驱动信号电压udr、补偿电感器L2的端电压uL2以及流过L2的电流iL2的波形。可见，采用并联双向TVS管的方法可以有效抑制电感产生的感应电动势。

图20 模式切换时电感器L2电压、电流波形

图21所示为充电模式切换时，逆变器输出电压uin、输出电流iin、充电电压UB、充电电流IB的波形。可以看出，切换时刻UB和IB基本保持稳定。

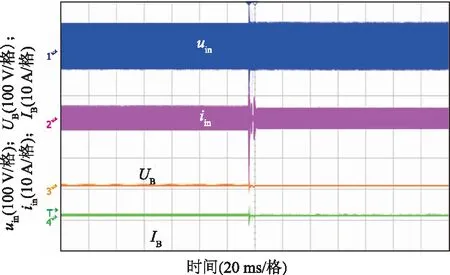
图21 模式切换时逆变器输出电压、输出电流、充电电压、电流波形

图22所示为系统的充电电流IB和充电电压UB随电池等效电阻RB的自然对数变化而变化的曲线。虚线左侧为恒流模式，虚线右侧为恒压模式。

图22 系统充电电流和充电电压随ln(RB/Ω)变化曲线

恒流充电时，IB从4.062 A逐渐下降到3.917 A，此过程中IB几乎保持恒定；恒压充电时，RB从12 Ω增大到72 Ω的过程中，UB从28.049 V逐渐上升到29.223 V，此过程中UB几乎保持恒定输出。

图23所示为系统效率η随着电池等效电阻RB自然对数变化而变化的曲线。恒流充电时，η基本维持在85%；恒压充电时，η由最初的89.67%先上升至91.1%，然后逐渐下降到最后的82.87%。整个充电过程中，η都维持在80%以上，保持ZPA充电，不引入无功功率，可以实现相对较高的充电效率。

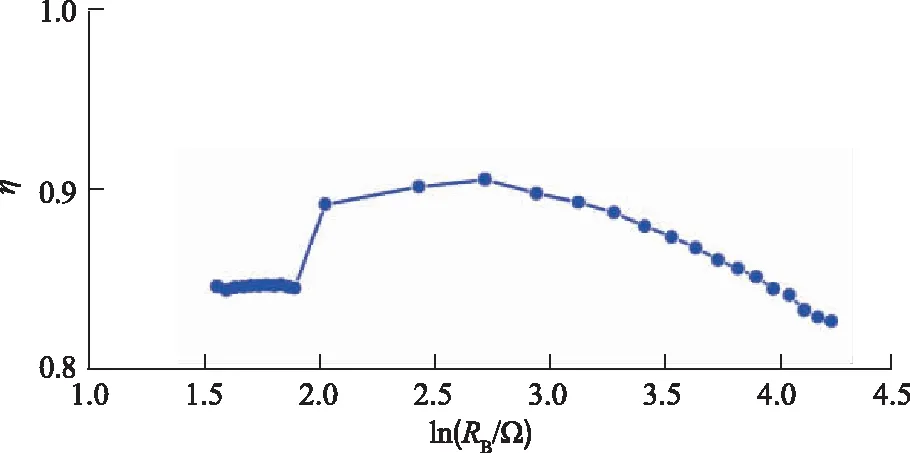
图23 系统效率随ln(RB/Ω)变化曲线

4 结论

本文提出一种基于三谐振的副边变补偿拓扑，实现IPT充电系统恒流和恒压切换输出。恒流模式下电流变化率仅为3.57%，恒压模式下电压变化率仅为4.19%，整体效率维持在80%以上，最高效率达91.1%。该方法恒压模式复用恒流模式的补偿元件，器件利用率较高，可降低部分无源元件和开关器件的电压和电流应力，一定程度上有利于移动设备小型化和降低系统成本；原边线圈电流恒定，可提高IPT系统效率，避免原副边通信，简化系统电路结构和控制复杂性，在“一对多”等需要原边工作稳定而不受副边复杂情况影响的应用场景中优势更明显。恒流模式可通过调节电感灵活设置系统工作于ZPA、ZVS或ZCS状态。在应用中可根据恒流充电需求来配置副边补偿电容，再据此匹配其他相关参数，实现多级恒流充电，提高功率等级，仅通过替换副边几个补偿元件就可以实现多级恒流多级功率输出，不局限于磁耦合机构的尺寸及参数。这种方法比重新设计磁耦合机构在时间和成本上都更具有优势，应用场景广泛。