三轴试样端部约束影响有限元分析
蒯青青,高 峰*,褚福永,孙鹏飞,朱俊高
(1.河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098; 2.丽水学院 工程与设计学院,浙江 丽水 323000;3.融创房地产集团有限公司,江苏 南京 210019)
三轴试验是研究土体强度和变形特性非常重要且广泛使用的试验,该试验操作简单,且能反映土体较复杂应力条件下的力学特性[1]。然而,端部约束效应是三轴试验真实存在且几乎无法避开的问题[2]。三轴试验本质上是单元体试验,理论上应该满足试样内部各处应力应变条件相同。但由于试样帽及试样底座的刚度远大于土体,导致受荷过程中试样与试样帽(及底座)之间存在摩擦力,从而一定程度上约束试样端部的变形,造成三轴试样内部应力和应变不均匀,此即三轴试样端部约束效应。由于端部约束效应,常规的三轴试验得到的试验结果并不能反映土体真实强度和变形特性[3],即试验结果必然存在误差[4-5]。国内外学者提出了多种方法试图弱化甚至消除三轴试验端部约束效应以获得更为准确的试验结果,如在试样端部增加过渡性垫块[6]、润滑试样帽[7]等。Rowe[7]设计了一种新型的试样帽(底座),主要由压力板、润滑剂和橡皮膜组成,因结构简单且能够有效减小端部约束而被广泛使用。陆晓平[2]等通过在三轴试样端部布置涂凡士林的乳胶膜来减轻摩擦力,比较了减摩与不减摩情况下砾石料的应力应变及强度性质。王君雄[8]基于将试样与试样帽间的滑动摩擦转变为滚动摩擦的减摩思路,设计了一种新型的减摩板,开展了粗粒土的常规和减摩三轴试验,分析了端部约束对粗粒土强度和弹性模量的影响。上述这些试验尽管在一定程度上减轻了端部摩擦力引起的约束效应,但无法完全消除。王助贫[9]采用数字图像测量技术,非接触量测了三轴试样的变形,对比传统方法测量的变形结果,定量研究了端部约束对变形的影响。以有限单元法为代表的数值模拟也是研究三轴试验端部约束效应的重要方法,其优点在于它可模拟完全无端部约束效应的情况,这是试验手段无法实现的。李云龙[10]通过有限元法分析了端部约束条件对三轴试样剪切过程应变区域的影响,认为端部约束会导致试样不同区域产生不同的应变,主要表现为中间区域大于两端。陈浩峰[11]利用有限元法研究了端部约束条件对三轴试样孔压和强度的影响,发现端部约束三轴试样加载过程中孔压变化率大,强度高。刘思远[12]曾对软土三轴排水剪试验进行有限元模拟,但没有进行不同状态下的土体试验比较,而且,对有无端部约束情况的应力应变及强度特性的差异缺少定量的比较分析,此法不能研究端部约束对强度性质的影响。
三轴试验可以通过一定方法减轻端部约束的影响,但无法完全消除。数值模拟则能完全消除端部约束,定量研究端部约束效应对三轴试样强度和应力应变性质的影响。目前对端部约束效应的定量研究有一些报道,但对不同状态下土体端部约束效应的相关定量研究仍有待深入,为此,本文针对某压实黏土和软土,进行完全限制端部径向位移和径向自由两种情况下三轴固结排水剪试验的有限元模拟,定量分析了端部约束条件对两种不同软硬程度土料的强度及应力应变性质的影响程度,可为常规三轴试验的力学参数修正提供参考。
1 有限元模型与模拟方案
理想的三轴试样是轴对称的,考虑到计算效率,选取标准中型三轴试样的1/4作为研究对象。图1给出了三维有限元模型网格,试样高200 mm,半径50.5 mm,共划分为480个6面体单元和714个结点,试样尺寸参考常规三轴试验的中型三轴试样(D×H=101 mm×200 mm)。图1中,T表示顶面,S表示扇形弧面,BC1和BC2分别表示两个垂直侧面,B表示底面。
本文针对试样端部有约束效应和端部径向变形自由的无端部约束情况分别进行模拟。两种情况的试样约束为:(1)端部有约束时,完全限制端部径向位移。底面B在X、Y、Z方向均约束,侧面BC1和BC2分别仅在X方向和Y方向约束,顶部T在X、Y方向约束;(2)端部径向自由(以下亦称为无端部约束或径向自由),底部B仅在Z方向约束,侧面BC1和BC2分别仅在X方向和Y方约束,顶部T无任何约束。
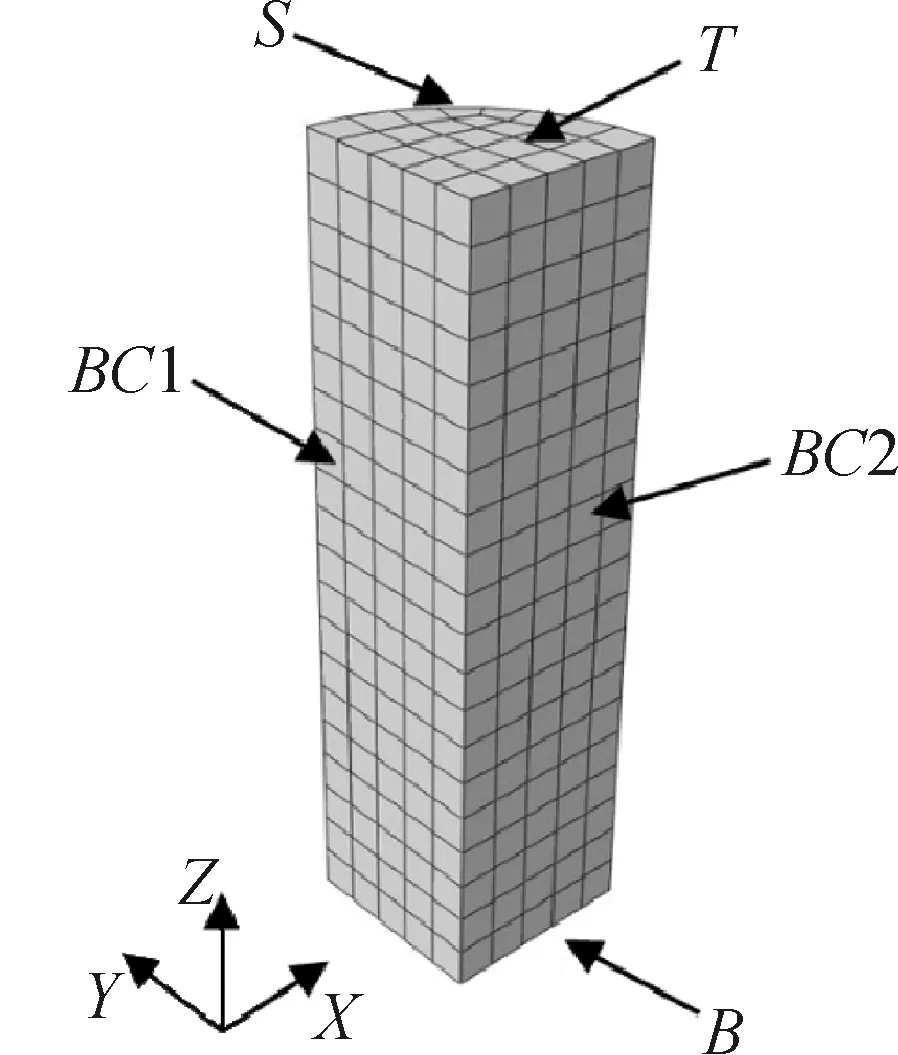
图1 三维有限元计算网格Fig.1 Three-dimensional finite element calculation grid
土体软硬不同,约束效应对应力应变性质影响程度可能存在差异,为此,对两种土料进行有限元模拟,分别是较硬的压实黏土和软土。计算模拟中,土体本构模型采用实际工程中应用较广的邓肯-张模型。两种土料的计算参数如表1所示,其中,压实黏土的参数取值参考某土石坝工程的接触黏土,软土的参数借用于文献[13],土质为上海软土[13]。

表1 邓肯-张模型参数Tab.1 Duncan-Chang model parameters
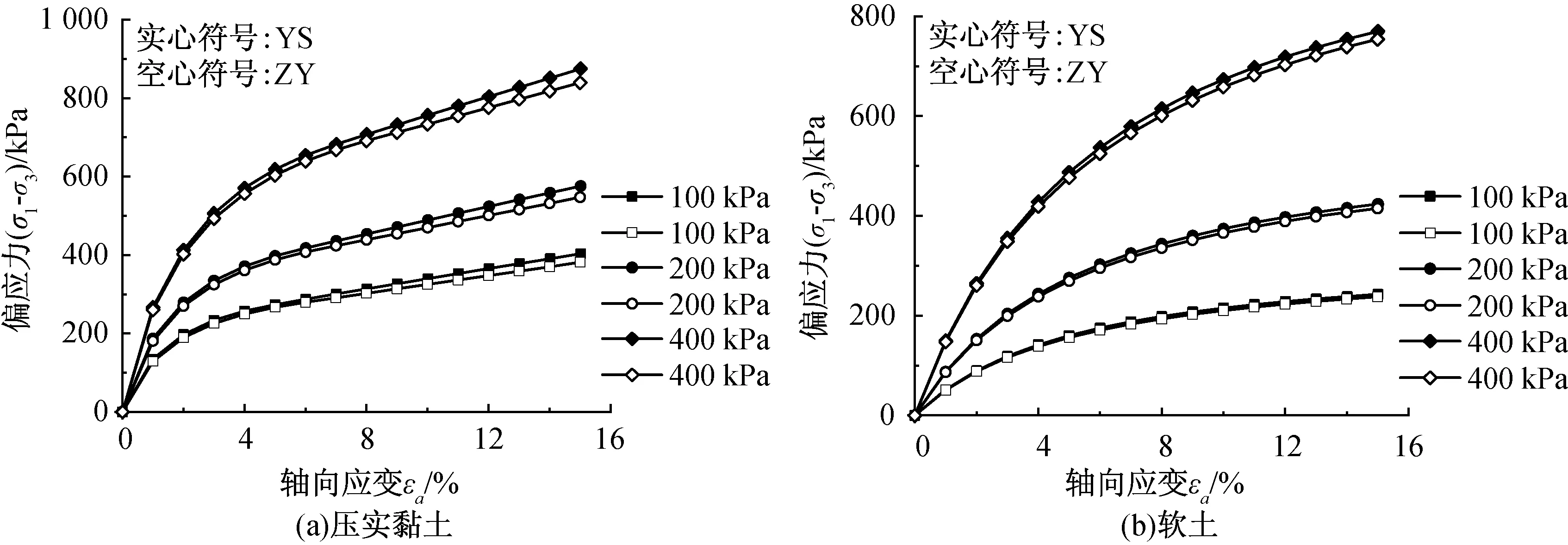
图2 两种土料的(σ1-σ3)-εa关系曲线Fig.2 Relation curves of (σ1-σ3)-εa of two soil materials
对压实黏土和软土分别对完全限制端部径向位移的常规三轴排水剪试验(下文以“YS”表示)和径向自由(无端部约束)的常规三轴排水剪试验(下文以“ZY”表示)进行计算模拟。加载过程参照常规三轴剪切试验,围压取100、200及400 kPa。
试样上的荷载分两步施加。首先,施加围压,即在S面和T面上施加数值等于围压的面力;然后,在T面分15级施加向下(向Z轴负方向)的位移,每级荷载下分了10个时间步;每级荷载时间内会产生1%的轴向应变,即2 mm位移,最后一级荷载时间完成后,试样轴向应变为15%。
2 端部约束影响分析
2.1 强度特性的影响分析
图2给出了压实黏土和软土的轴向偏应力(σ1-σ3)和轴向应变εa的关系曲线。可以看出,无论是压实黏土还是软土,在不同围压下,两种端部约束条件模拟的(σ1-σ3)-εa关系曲线整体规律类似,都呈现一直上升的趋势直至破坏,表现为压硬性。进一步对比(σ1-σ3)-εa关系曲线可以发现,小应变下,两种端部约束条件的应力应变曲线高度吻合,与陈春霖的砂土试验结果一致[14]。当轴向应变较大时,端部约束(YS)试样的曲线都位于无端部约束(ZY)曲线的上方,同一轴向应变εa下,有端部约束的(σ1-σ3)总大于无端部约束。说明受端部约束作用,土体强度有所提高,这与董建军[3]的试验结论相同。
表2列出了在不同围压时,压实黏土和软土在两种端部约束条件下,剪切破坏的峰值(应变15%)偏应力(σ1-σ3)f及端部约束对强度造成的相对误差(以“Rσ”表示),Rσ为端部约束与径向自由的峰值偏应力的差值与径向自由峰值偏应力的比值。可以看出,端部约束对峰值偏应力(σ1-σ3)f有一定的贡献,贡献幅度在2%~6%,不同围压下压实黏土和软土Rσ的平均值分别为5.2%和2.1%。
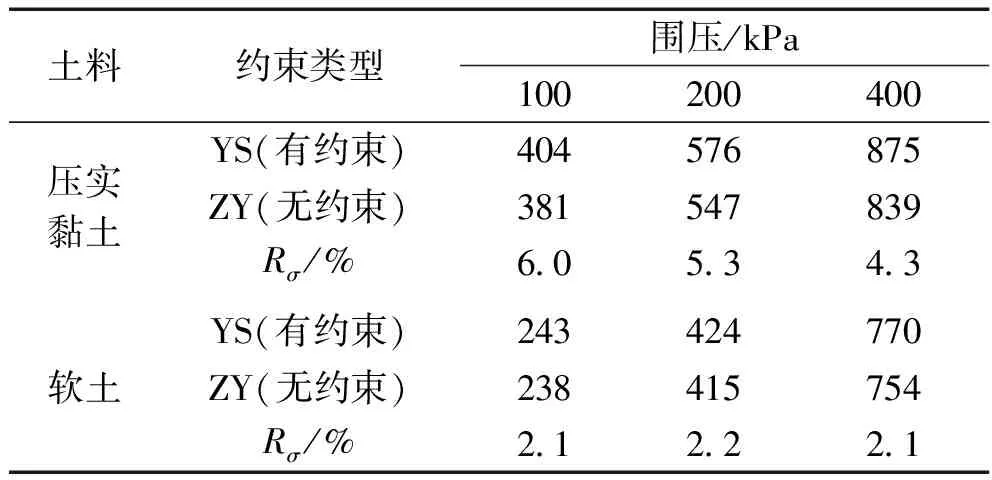
表2 模拟的偏应力(σ1-σ3)f峰值Tab.2 Peak values of (σ1-σ3)f for simulation
从表2还可以看出,有约束与无约束试样(σ1-σ3)f差值随着围压的增大而增大,但是,对压实黏土,相对误差Rσ则随围压增大而减小。由于这里Rσ实际上是描述试样因端部约束而引起的试验结果的误差,因此,应以Rσ来表述约束效应的强弱,而不应用绝对差值来表示。因此,可以认为,对较硬的土,端部约束对强度的影响随围压增大而减弱。对于软土,Rσ几乎不受围压的影响,说明围压对软土端部约束下强度的影响较小。
2.2 变形特性的影响分析
图3(a)、(b)分别为压实黏土数值试样在端部约束和径向自由下轴向应变εa为15%的网格变形图。可以看出,端部约束条件下,试样中间部位有鼓胀,与实际三轴试验变形结果相似;径向自由条件下,试样各处侧向应变相同,为理想三轴试验的试样变形结果。

图3 端部约束对试样侧向变形的影响(εa=15%)Fig.3 Effects of end restraint on lateral deformation of specimen (εa=15%)
图4给出了压实黏土和软土的体积应变(简称体变)εv和轴向应变εa的关系曲线。可以看出,试样在整个剪切过程中表现为剪缩,围压越大,剪缩变形也越大。在相同εa下,端部约束试样的体变εv总体上比径向自由试样大。相同围压下,端部约束试样的体变εv和轴向应变εa关系曲线在小应变下比径向自由试样的曲线略陡。随着轴向应变εa的增大,压实黏土和软土的体变εv受端部约束影响的程度增大,且压实黏土体变εv受端部约束的影响程度远高于软土。说明对于不同物理力学性质的土体,端部约束对体变的影响有显著差异。
为定量研究端部约束对压实黏土和软土体变εv的影响规律,表3列出了不同围压下,压实黏土和软土剪切破坏时的体变εv值及端部约束对体变造成的相对误差(下文以“Rv”表示),Rv表示为土体剪切破坏时,端部约束与径向自由体变的差值与径向自由体变的比值。可以看出,端部约束效应对试样体变影响较大,压实黏土围压100 kPa时,有约束试样的体变比无约束时增大了25%。笔者认为,这种影响已经到了不可忽略的程度。
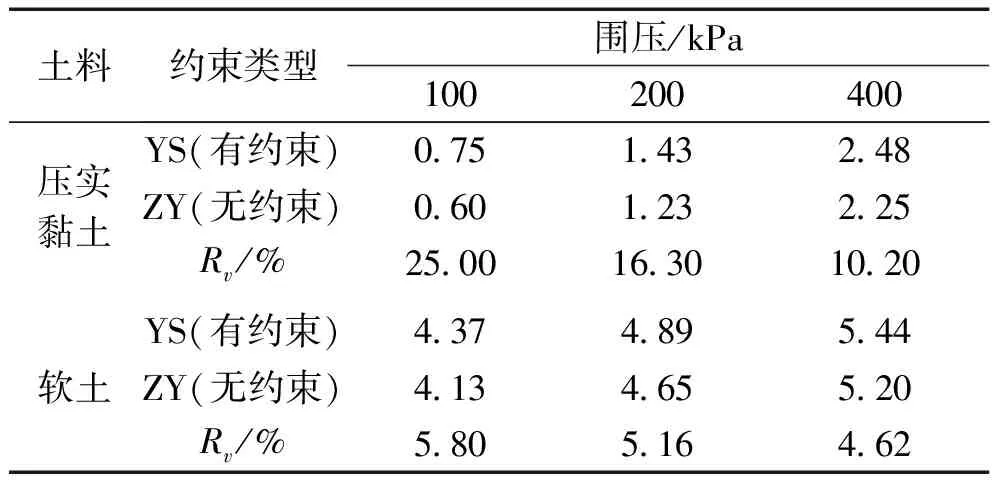
表3 剪切破坏时的体变εv值Tab.3 Volume strain εv value at shear failure
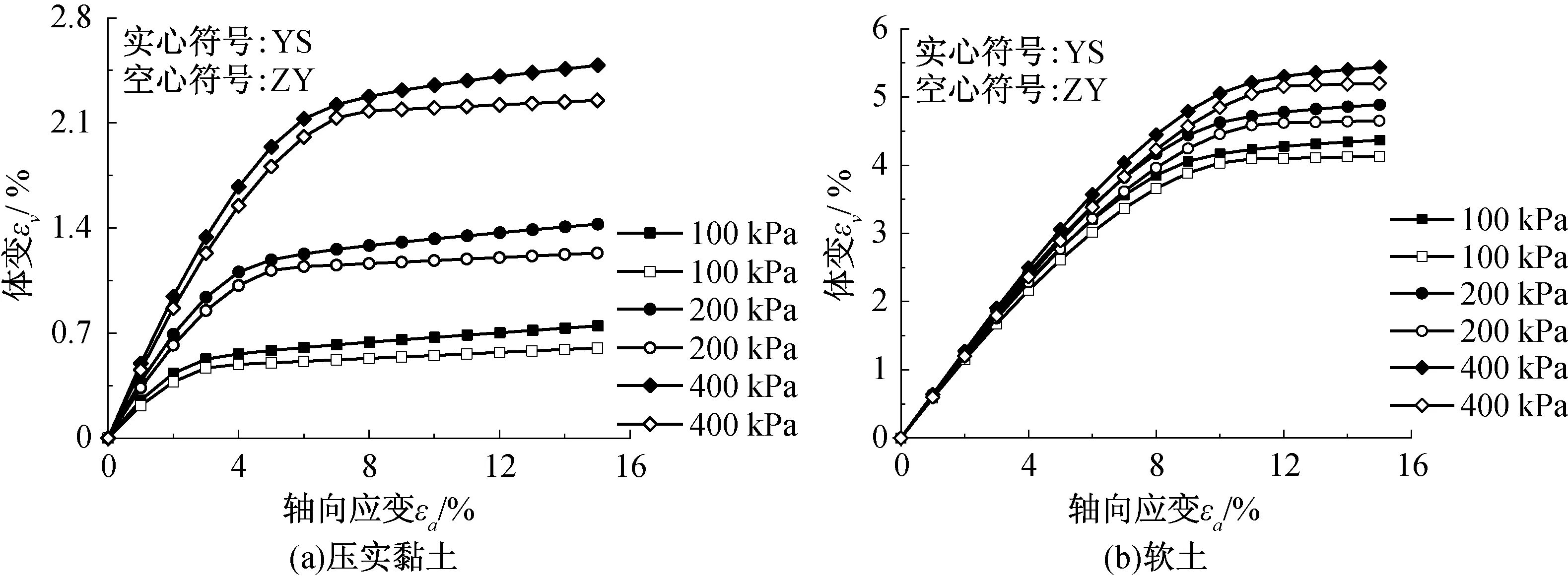
图4 两种土料的εv-εa关系曲线Fig.4 Relation curves of εv-εa of two soil materials
另外,对不同土质,约束效应的影响程度也是不同的。对于压实黏土,端部约束试样剪切破坏时(各单元)平均体变εv比径向自由增大17.2%;对软土该值为5.2%。
2.3 试样内应力状态分析
三轴试验为单元体试验,理想三轴试样内各点的应力状态是相同的,各点的大、小主应力值应该相等。但是,实际三轴试验中,由于端部约束效应,试样内各处应力分布是不均匀的,其不均匀程度到底如何,还未见有相关研究,这里进行详细分析。
图5(a)、(b)分别给出了围压400 kPa情况下,软土剪切破坏时,两种端部约束条件试样中轴线位置和试样边缘处的大、小主应力沿着试样高度方向分布。图5(c)显示了该试样端部一层单元内大、小主应力沿径向的分布。
由图5可以看出,径向自由(ZY,即无端部约束)情况,无论是沿高度还是径向,应力分布均匀,符合理想三轴试验的应力状态。图5(a)显示,对试样端部有约束情况(YS),小主应力σ3沿高度方向呈现中间小,两端大的分布规律,端部约束效应对小主应力影响明显。大主应力σ1沿着试样高度方向的分布也受到端部约束的显著影响,试样1/2高度处及端部σ1值均较小,在1/5和4/5高度处σ1值最大,其值比无端部约束情况大7%。从图5(b)可以看出,在试样边缘处,大小主应力沿高度方向分布的均匀程度明显比试样中轴线处好,仅仅在试样最端部的一层单元内应力稍大。从图5(c)可以看出,有端部约束情况下,试样端部位置处小主应力沿径向分布表现为随着与中轴线距离的增大而逐渐减小,而且其值都大于无端部约束的情况,中轴线处最大,比无约束时大7.2%。
大主应力σ1沿径向分布也不均匀,其值在靠近试样边缘位置处大于无端部约束的情况,靠近中轴线的区域其值反而小于无端部约束的情况。
总之,端部约束会引发试样内部应力分布不均匀,最终导致三轴试验结果与所期望的理想状态出现偏差。压实黏土的大小主应力分布规律类似,不再重复论述。
上节的分析表明,约束效应对试样体变影响较大。为从力学机理上对其解释,整理了围压400 kPa下,压实黏土和软土分别在端部约束和径向自由条件下,试样轴向应变15%时的大主应力、小主应力及平均正应力p,列于表4可以看出,无论是压实黏土还是软土,端部约束试样的大、小主应力及平均正应力均大于径向自由的情况。已有三轴试验的经验表明,围压(小主应力)越大,对应试验得到的试样体变也越大,而且,已有理论及经验均表明,体积应变与p密切相关,因此,端部约束试样体变必然大于无端部约束试样的体变。
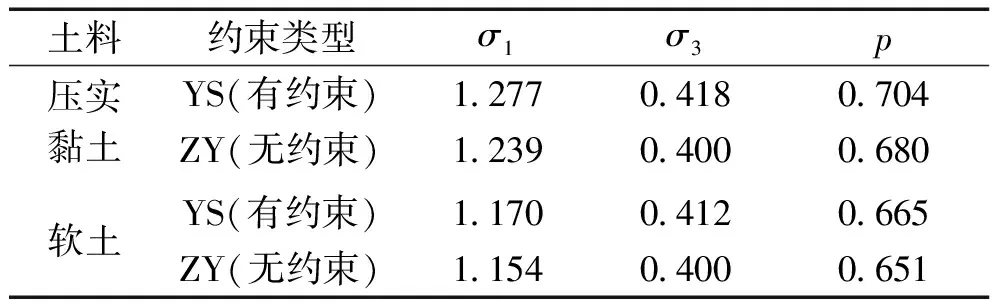
表4 围压400 kPa的试样应力状态(εa=15%)Tab.4 Stress state of specimen with confining pressure of 400 kPa (εa=15%)
3 结论
本文对某压实黏土和软土在完全限制端部径向位移和径向自由(无端部约束)条件下,进行了常规三轴试验的有限元模拟,定量研究了端部约束对强度及应力应变特性的影响,主要结论如下:
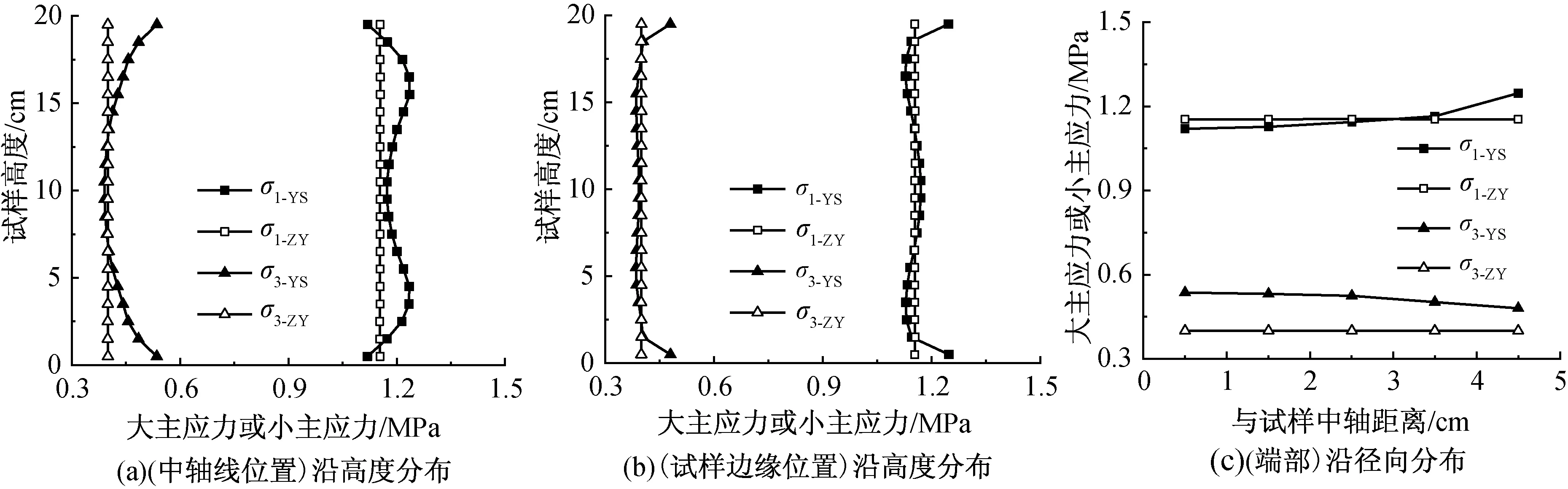
图5 软土大小主应力沿试样高度和径向的关系Fig.5 Relationship between major and minor principal stresses of soft soil along sample height and radial direction
1)端部约束对土体强度有一定提高,对峰值偏应力(σ1-σ3)f有一定的贡献,两种土料的贡献幅度均在2%~6%之间,但不会改变偏应力和轴向应变关系曲线的整体趋势;随着围压的增大,端部约束对强度的影响略有降低,但降低幅度有限。
2)端部约束对体变影响显著,压实黏土100 kPa时,端部约束试样剪切破坏时的平均体变εv比无端部约束试样增大了25%;随着围压增大,这种影响的程度减弱。
3)对不同软硬程度的土料,端部约束对体变的影响程度差异较大;相比径向自由情况,压实黏土剪切破坏时的平均体变εv增大17.2%,软土增大5.2%;土体越硬,端部约束效应越明显。
4)端部约束会引发试样内部单元应力分布不均匀,最终导致试样力学特性差异;端部约束引起试样内部小主应力平均值显著增大是导致端部约束对体变影响显著的重要原因。

