基于最大能量耗散率原理的黄土本构模型参数的研究

付成博，范 文,2,3，邓龙胜,3，马利锋，魏亚妮,3*

(1.长安大学 地质工程与测绘学院，陕西 西安 710054；2.信息产业部电子综合勘察研究院，陕西 西安 710054； 3.西部矿产资源与地质工程教育部重点实验室，陕西 西安 710054；4.西安交通大学 工程力学系，陕西 西安 710049)

在分析黄土应力-应变的关系时，工程上常用到的本构模型一般分为两类[1-7]：第一类是弹性模型，主要是将岩土体视为弹性体，从而建立起线性或者非线性的应力-应变关系，例如Love提出线弹性模型和邓肯等人提出的一些非线性弹性模型[8]，但黄土不能简单地被视为弹性或非线性弹性材料，这些模型在用于单调加载的情况时的结果得到较为准确，但用于复杂加载的情况时，结果往往不能符合工程的要求[9-10]；第二类是弹塑性模型，以Drucker公设和Iliushin塑性公设为理论基础，借由经典塑性力学本构中的屈服条件、流动法则、硬化规律等几个要素，通过数学推导得到其本构模型，例如Lade-Duncan模型、剑桥模型等[11]，但许多学者经过研究和试验后[12-16]，认为塑性力学中的几个要素在岩土体本构中往往都是单独确定的，不够严谨，从而导致在一些应力路径上会出现违反热力学基本定律的情况[17]。西安交通大学马利锋教授认为应该从热力学第一定律和第二定律出发，同时将最大能量耗散率原理视为同等的热力学定律，以此建立起弹塑性增量本构模型，其本构模型遵循热力学基本定律[18]，能很好地描述黄土的应力应变关系。

本文基于前人的研究，选择泾阳南塬为研究区域，设计出一套适用于基于最大能量耗散率原理的黄土本构模型的试验方案，确定其硬化函数的形式，研究在不同含水率下该本构模型参数的取值范围，并验证模型及参数的准确性。

1 基于最大能量耗散率原理的黄土弹塑性本构模型

本文采用西安交通大学马利锋教授提出的基于最大能量耗散率原理的黄土弹塑性本构模型[18]，其本构模型的基础理论是热力学第一定律和第二定律，并将最大能量耗散率原理视为等同的定律。下文将简单介绍其本构模型的主要内容。

(1)

在变形过程中，应满足热力学第一定律和热力学第二定律：

(2)

(3)

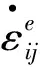
(4)

将应力(应变)分解成体积和偏差分量：

(5)

式中：σm—静水应力；εv—体应变；sij—偏应力；eij—偏应变。

对于各向同性材料的塑性变形，式(4)要求满足最大能量耗散率原理，并且由于sii=0，eii=0，式(4)可以重新写成：

(6)

在塑性变形过程中的任何时候，变形能耗散率与等张变形能耗散率是独立的，但应同时满足最大能量耗散率。即塑性变形方向应与相应的应力方向相同：

(7)

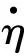
(8)

(9)

结合式(1)和弹性力学相关公式，增量弹塑性本构关系为：

(10)

式中：G—剪切模量，MPa；K—体积模量，MPa。

式(10)即为基于最大能量耗散率原理推导出的增量弹塑性本构模型。

2 针对模型参数的试验设计

2.1 模型参数

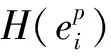
通过不同含水率和围压的三轴试验表明，泾阳南塬Q3马兰重塑黄土体呈现应变硬化型特征，弹性参数参考邓肯-张(Duncan-Chang)模型[8]，通过其剪应力-轴向应变关系的曲线计算获得各工况下的弹性模量Ei和泊松比υ，然后利用弹性力学相关公式计算获得剪切模量G和体积模量K。

参考简布对压缩试验的研究，拟合获得土体弹性模量随围压变化的公式：

(11)

式中：k—拟合参数；n—拟合参数；σ3—围压，kPa；Pa—标准大气压，101.4 kPa。

在室内三轴试验应力条件下σ2=σ3，试样的应力状态可以由下式表示：

(12)

si=σ1-σ3

(13)

对于应力应变的定义，土的应变状态可以分解为纯体积应变εv和剪切应变ei(即偏应变不变量)。在室内三轴试验应力条件下ε2=ε3，试样的体应变εv和剪应变ei可以由下面两式表示：

εv=ε1+2ε3

(14)

(15)

式中：ε1—轴向应变，%；ε3—侧向应变，%。

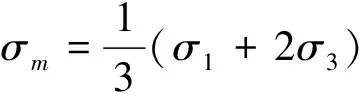
(16)

(17)

(18)

(19)

式中：a—拟合参数；b—拟合参数。

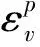
患者的放射治疗情况采用WHO实体瘤临床疗效判定标准进行评价，其中完全缓解（CR）即肿瘤病灶完全消失1个月以上；部分缓解（PR）指的是肿瘤病灶未消失但明显减小50%以上，持续1个月以上，期间未见新病灶形成；稳定（SD）：肿瘤病灶缩小面积不足50%或增大25%以内均判定为稳定；病情进展（PD）：肿瘤病灶增大超过25%，甚至复查时发现新发或转移肿瘤病灶均可定义为病情进展。总有效率为完全缓解与部分缓解患者比例之和。

(20)

式中：m1—拟合参数；m2—拟合参数；m3—拟合参数。

2.2 针对模型参数的试验方案设计

工程上黄土含水率范围通常在5%到20%之间[22]，在此范围内，选定10%、14%、18%三组含水率，通过一次性静压力制样法压制干密度为1.30 g/cm3的重塑土样，使用英国GDS公司生产的非饱和应力路径的三轴仪进行固结不排水试验，具体试验工况见表1。

表1 试验工况Tab.1 Test conditions

3 模型参数取值及验证

3.1 研究区概况

本文试验所用的试样取于泾阳南塬的Q3马兰黄土，其基本的物理力学指标如表2所示。

表2 泾阳南塬的Q3马兰黄土基本物理指标Tab.2 Basic physical indexes of Q3 Malan loess in Southern Jing-Yang plateau

3.2 弹性参数

由试验一，可得不同含水率下的应力-应变曲线，如图1所示，来确定模型的弹性参数。

图1 不同含水率的土体应力-应变曲线Fig.1 Stress-strain curves of soil with different moisture contents

参考土工试验规范，拟合计算其初始弹性模量Ei(MPa)，其结果见表3。

表3 不同围压下不同含水率的初始弹性模量Ei (单位：MPa)Tab.3 Initial elastic modulus Ei of different moisture contents under different confining pressures

通过拟合计算出的初始弹性模量Ei(MPa)，按式(11)进行拟合参数k、n，其拟合结果见图2，其结果见表4。

图2 不同含水率的土体弹性模量拟合结果Fig.2 Fitting results of elastic modulus of soil with different moisture contents

表4 不同含水率的弹性模量Ei的参数k、nTab.4 Parameters k、n of elastic modulus Ei of different moisture contents

试验表明，参数k取值在0.5至1.5之间，随含水率增大而逐渐减小；参数n取值在0.04至0.3之间，随含水率增大而增大。

参考土工试验规范计算得出泾阳南塬Q3马兰黄土在不同固结围压下的泊松比υ值近似相等，结果如表5所示。

通过弹性力学相关公式，计算获得体积模量K、剪切模量G。试验结果表明，泾阳南塬Q3马兰黄土泊松比为0.3，可视为常数；弹性模量Ei取值在50 MPa至150 MPa之间，体积模量K取值在40 MPa至130 MPa之间，剪切模量G取值在20 MPa至60 MPa之间。

表5 不同围压下不同含水率的泊松比υTab.5 Poisson’s ratio υ of different water contents under different confining pressures

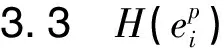
图硬化函数拟合结果Fig.3 Fitting results of hardening function

表硬化函数拟合参数a、b结果Tab.6 Results of hardening function fitting parameters a and b

试验表明，同一围压下在相同的剪应力下，随含水率增大塑性剪应变增大，并且围压越大，塑性剪应变越小。参数a取值范围在0.002至0.02之间，随含水率增大而增大，随围压增大而减小；参数b取值范围在0.01至0.05之间，随含水率增大而增大，随围压增大而减小。

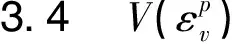
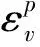
图硬化函拟合曲线Fig.4 Fitting results of hardening function

表硬化函数拟合参数m1、m2、m3结果Tab.7 Results of hardening function fitting parameters m1,m2 and m3

试验表明，相同的静水应力下，塑性体应变随含水率增大而增大，曲线呈躺倒的“反S”型，即在静水应力较小时，未产生大量的塑性体应变，以弹性应变为主，初期塑性体应变值较小，曲线初始斜率较大；随着静水应力增大，开始产生大量塑性体应变，中期塑性体应变增量较大，曲线的中期斜率变小；但随着静水应力进一步增大，试样变形达到极限值，大多数孔隙已经被压缩，试样被进一步压实，没有更多孔隙可以被压缩，塑性体变增加变小，曲线的后期斜率变大，最后趋近于一个极限值。参数m1取值在0.5至1之间，m2取值在0.05至1之间，m3取值在0.001至0.01之间。

3.5 模型参数验证

通过上文试验确定的参数，基于试验一的试验数据，验证在不同工况下基于最大能量耗散率原理的黄土弹塑性本构模型的适用性，其结果如图5所示。

图5 本构参数及模型的验证Fig.5 Validations of constitutive parameters and model

拟合结果表明，基于最大能量耗散率原理的黄土弹塑性本构模型，使用通过本文试验方案确定出的硬化函数形式以及拟合得出的参数，经验证后能够准确地反映常规三轴试验下泾阳南塬的Q3马兰黄土的应力-应变关系。

4 结论

2) 泾阳南塬Q3马兰黄土体积模量K取值在40 MPa至130 MPa之间，剪切模量G取值在20 MPa至60 MPa之间；塑性参数a取值在0.002至0.02之间，参数b在0.01至0.05之间，参数m1取值在0.5至1之间，m2取值在0.05至1之间，m3取值在0.001至0.01之间。

3) 对基于最大能量耗散率原理的黄土弹塑性本构模型进行验证，验证结果表明该本构模型通过本文试验方案取得的模型参数能够准确描述泾阳南Q3马兰黄土在三轴剪切下的应力-应变关系。