基于矢量匹配法的复杂土壤环境下接地棒雷击暂态电路模型研究
周玉娟
(江苏开放大学建筑工程学院,南京 210036)
0 引言
作为电力系统的重要组成部分,防雷接地装置与电气一、二次回路和电气设备密不可分,其是否合理有效,严重影响着电力系统的正常运行。随着高压、超高压、特高压输电网的普及,系统接地短路电流越来越大[1],地网暂态电位抬升也越来越高,对于保障人身、电气设备以及抗干扰能力较弱的电子设备安全防雷接地系统提出了更高的要求。
国内外学者通过现场试验[2]、模型实验[3]、仿真计算[4]等手段对于防雷接地技术进行了大量研究,取得了长足进展。数值仿真方法虽与实际情况存在一定偏差,但因其具备高效、简便等优点,仍然得到最为广泛地应用,通过FEM[5]、FDTD[6]等算法建立电磁场、EMTP[4]等软件建立电路模型,分析接地装置的电流、电压暂态特性是较为常用的仿真手段。
相关学者对接地棒等值电路模型进行了深入研究,考虑了土壤水平双层、水平多层情况[7],分析了土壤反射系数、不同土壤层厚度对接地性能的影响[8],但是目前对于土壤垂直分层情况的研究则相对偏少,海陆交界、滩涂、丘陵等地区土壤复合性较强[9],不仅有水平方向变化,也有垂直方向变化,采用不合适的模型分析导致实际值与设计值大相径庭,也会带来工程隐患,因此有必要进一步研究复杂土壤结构下接地棒暂态电路模型。
本研究以海陆混合环境为例,利用矢量匹配法结合最小二乘法确定电路模型参数,建立接地棒暂态电路模型,通过EMTP软件计算雷电流作用下接地棒电位抬升,分析土壤环境参数对暂态电位抬升的影响。
1 接地棒暂态电路模型
由于雷电流波头陡度较大,相应等值频率很高,在雷电流作用下,接地棒集总参数模型难以体现暂态传输特性,接地体不仅有电阻、电导参数,而且还具有电感、电容参数,目前较为常用的接地棒电路模型是有损长线分布参数模型[4,10],每段导体由电感、电容、电导和电阻组成,沿着接地棒分布。图1给出了均匀土壤下接地棒暂态电路模型[4]。
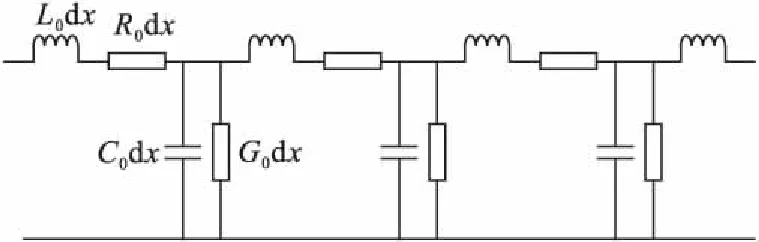
图1 接地棒暂态电路模型Fig.1 Transient circuit model of the grounding electrode
图1中R0和L0分别为水平接地极单位长度传递电阻和电感,C0和G0分别为单位长度对地电容和对地电导。电路模型参数可以根据公式代入接地棒尺寸、接地棒材料电阻率和磁导率、埋深、土壤电阻率等参数求取[4]。
大部分情况下,土壤电阻率分布是不均匀的,土壤分层情况下不能够直接计算出图1中接地棒暂态电路模型参数,为此可以将土壤电阻率进行近似等效,将双层土壤等效为单层均匀土壤,见图2[11]。
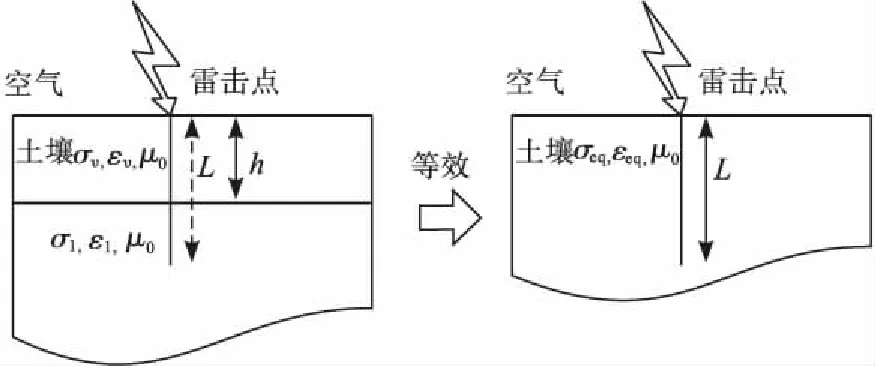
图2 双层土壤等效模型Fig.2 Equivalent model of horizontally two-layered soil
需要指出的是,涉及到复杂边界匹配问题[12],类似图3给出的复杂土壤环境下,接地棒暂态传输线模型已不再适用。
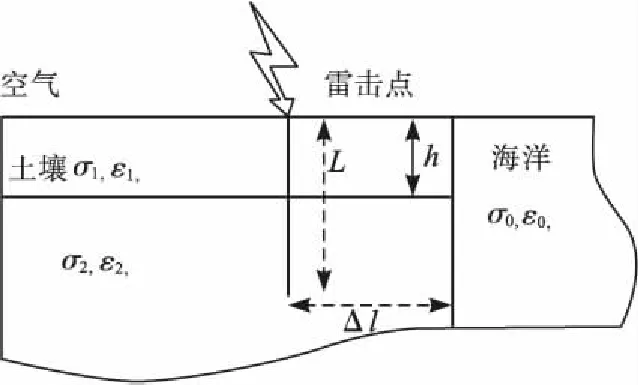
图3 复杂土壤环境土壤模型Fig.3 Equivalent model of soil in ocean-land mixedenvironment
针对这种复杂情况,采用的思路是利用FEM计算接地棒的冲击阻抗,然后采用矢量匹配法[13-14]对接地棒特性导纳参数进行有效拟合,使得新的暂态电路模型仍然具有分布参数电路基本形式。
2 电路参数拟合
2.1 矢量匹配法
接地棒频域响应f(s)拟合采用有理函数,具有如下近似表达形式[15-16]:
(1)
式中,an为未知极点,cn为留数,设an和cn为共轭复数对或实数,d和h为实数。
由于极点an出现在分母中,导致由式(1)确定未知量an、cn、d和h是一个非线性问题,利用矢量匹配法先定位极点an使其变为已知,式(1)便转化成未知量cn、d和h的非线性问题。
用一个N阶未知有理函数θ(s)乘以f(s):
(2)
(3)

将f(s)所得新极点作为初始极点重复迭代计算,直至θ(s)趋近于1为止。
2.2 特性导纳拟合
采用矢量匹配法可得接地棒特性导纳Yc(ω)的近似有理式表达[16]:
(4)
由于式(4)中an、cn为共轭复数,因此进行分式合并后有:
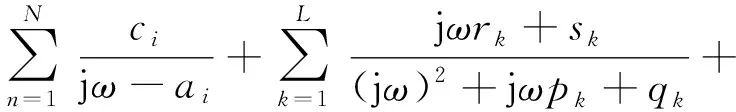
d+jωh
(5)
式中,N=M+2L。
式(5)中d+jωh类似电导G0和电容C0并联支路的导纳G0+jωC0;ci/(jω-ai)类似电阻Rr和电感Lr串联支路的导纳1/(Rr+jωLr)或电阻Rr和电容Cr串联支路的导纳为Rr/(Rr+jωCr);(jωrk+sk)/[(jω)2+jωpk+qk]类似于电导、电容并联和电阻、电感串联后形成的复杂支路的导纳(Gc+jωCc)/[(Rc+jωLc)(Gc+jωCc)+1]。因此,接地棒特性导纳Yc(ω)可用图4所示的暂态电路进行等效[17]。
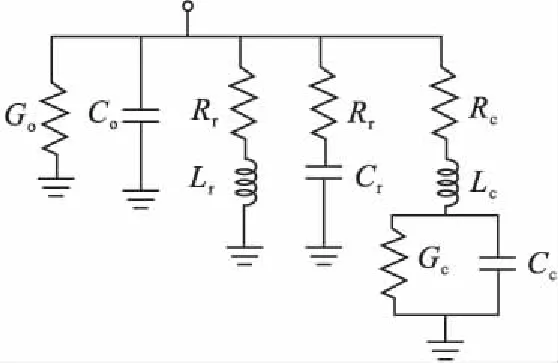
图4 基于矢量匹配法的接地棒等值电路Fig.4 Equivalent circuit of the grounding electrode based on VFM
图4中电路参数与式(5)中参数存在如下对应关系:G0=d,C0=h;Rr=-ai/ci,Lr=1/ci或Cr=-ci/ai2;Lc=1/rk,Rc=(pk-skLc)Lc,Cc=1/[(qk-skRc)Lc],Gc=skCcLc。
3 仿真分析
3.1 雷电流波形
雷电主放电电流波形采用目前应用最为广泛的Heidler函数[18],具体表达式为
(6)
式中,I0主放电电流峰值;τ1和τ2分别为波形上升沿和下降沿时间常数,η为峰值修正因子,n为电流陡度常数。
CIGRE[19]推荐雷电流波形为:波头时间3.83 μs,波尾时间77. 5 μs,幅值31.1 kA。
3.2 接地棒电路
表1给出了接地棒参数和两种不同土壤分层情况下土壤和海洋环境参数,分别是上层土壤电阻率低于下层和下层土壤电阻率低于上层。
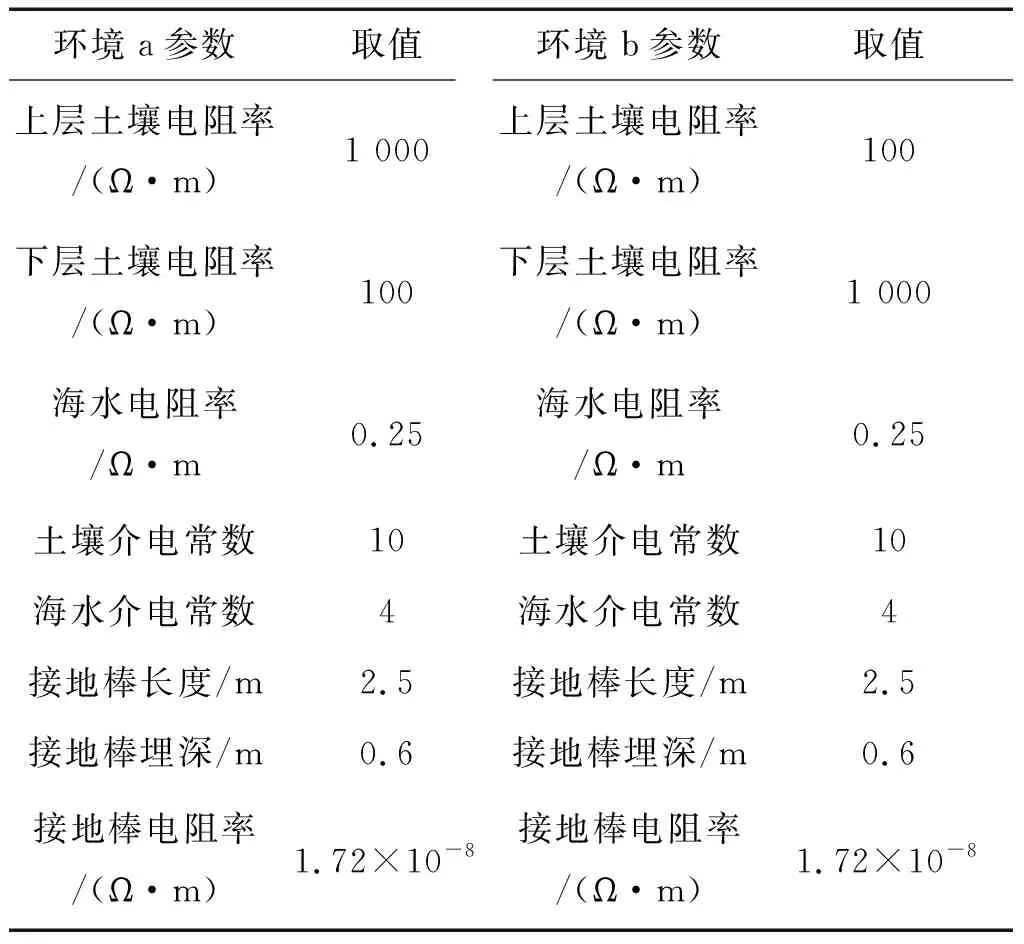
表1 接地棒和环境参数Table1 Parameters of the horizontal grounding electrode and the ocean-land mixed environment
图5给出了通过矢量匹配法计算获得的环境a中接地棒阻抗特性曲线,包括幅频特性与相频特性。接地棒距海陆交界处水平距离为5 m。

图5 基于矢量匹配法的双层土壤环境中接地棒冲击阻抗特性曲线Fig.5 Input characteristicimpedance of the grounding electrode buried in horizontally two-layered soil using VFM
由图5可知,接地棒低频阻抗幅频和相频变化不明显,随着频率的增加,高频阻抗的变化相对较大,因此在计算雷击暂态电位抬升时必须考虑高频阻抗部分产生的影响。
根据矢量匹配法求取的最终极点和留数,拟合环境a中接地棒暂态电路模型,见图6。

图6 考虑海洋环境影响前后环境a中接地棒暂态电路模型Fig.6 Equivalent circuit of the grounding electrode buried in horizontally two-layered soil for the environment a without and with ocean effect
图6可以看出,考虑海洋环境影响与否对接地棒暂态电路模型影响明显,尤其是电路模型中电容参数变化较大。
同理,图7给出了考虑海洋环境影响前后环境b中接地棒暂态电路模型。
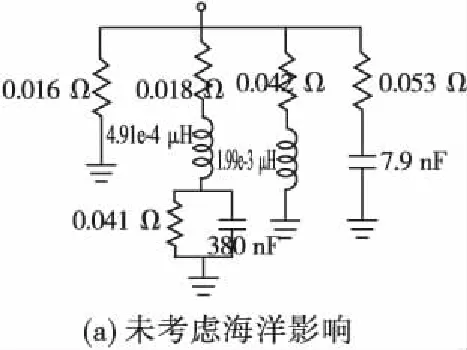
图7 考虑海洋环境影响前后环境b中接地棒暂态电路模型Fig.7 Equivalent circuit of the grounding electrode buried in horizontally two-layered soil for the environment bwithout and with ocean effect
3.3 暂态过电压
图8给出了环境a中,距海洋不同水平距离情况下接地棒暂态电位抬升。

图8 距海洋不同水平距离下环境a中接地棒暂态电位抬升Fig.8 Grounding potential rise of the grounding electrode buried in horizontally two-layered soil for the environment a with different distance from the neighboring ocean
由图8可以看出,上层土壤电阻率高于下层土壤电阻率环境中,雷电流注入点接地棒暂态过电压波形较为类似,均是上升沿较为陡峭,下降较为缓慢,但是暂态电位抬升幅值变化差异较大,越远离海洋,接地棒暂态电位抬升幅值越高。但是当接地棒距海洋距离超过15 m后,暂态电位抬升幅值增加趋势明显趋缓,增幅低于5%。
图9给出了环境b中不同情况下接地棒暂态电位抬升。

图9 距海洋不同水平距离下环境b中接地棒暂态电位抬升Fig.9 Grounding potential rise of the grounding electrode buried in horizontally two-layered soil for the environment b with different distance from the neighboring ocean
由图9可以看出,上层土壤电阻率低于下层土壤电阻率环境中,接地棒暂态过电压波形也较为接近。明显不同于上层土壤电阻率高于下层土壤电阻率环境的是,接地棒越接近海洋,暂态电位抬升幅值越高。但是同样当接地棒距海洋距离超过15 m 后,暂态电位抬升幅值降低趋势明显减缓,减幅也低于5%。因此,当接地棒距邻近海洋环境距离超过15 m时,海洋环境的影响大为减小,可以近似忽略不计。
3.4 土壤分层厚度影响
图10给出了两种不同环境下,上层土壤厚度对接地棒暂态电位抬升的影响。
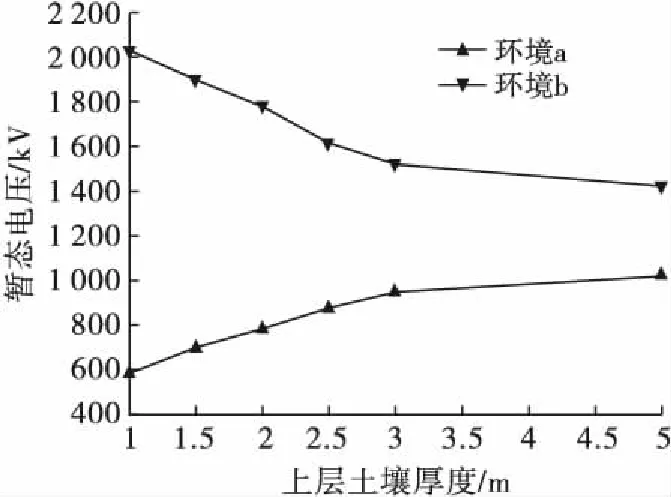
图10 上层土壤厚度对接地棒暂态电位抬升影响Fig.10 Influence of thickness of the first layer on grounding potential rise of the grounding electrode
图10可以看出,随着上层土壤厚度的不断增加,上层土壤电阻率高于下层土壤电阻率环境中接地棒暂态电位抬升逐渐增大,上层土壤电阻率低于下层土壤电阻率环境中接地棒暂态电位抬升逐渐降低,这表明暂态电位抬升受上层土壤的影响不断增大,最终暂态电位抬升趋于稳定值,这个稳定值是由上层土壤电阻率所决定的[20]。
3.5 雷电流波头时间影响
为进一步确定海洋环境对接地棒模型的临界影响距离,图11给出了不同雷电流波头时间下接地棒暂态电位抬升减幅恰好小于5%时对应的距离。
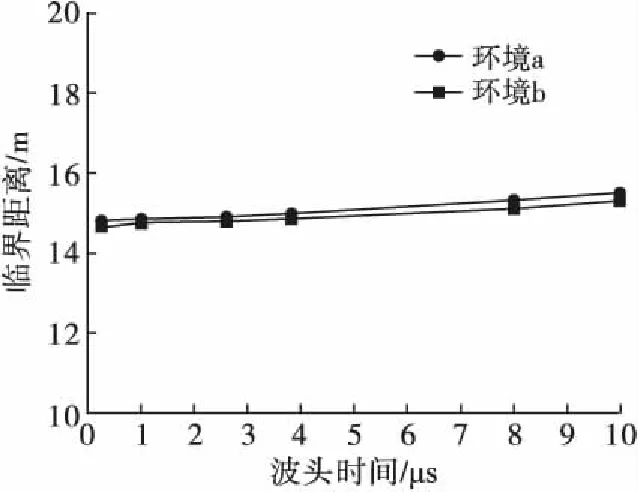
图11 波头时间对临界距离的影响Fig.11 Influence of wave front time on the critical distance
图11可以看出,随着雷电流波头时间的增大,海洋环境对接地棒模型的临界影响距离有所增大,但是增加幅度不明显,说明临界影响距离受波头时间和雷电流陡度影响不大。
4 结论
通过矢量匹配法拟合复杂土壤环境下接地棒暂态电路模型参数,利用EMTP软件分析接地棒雷击暂态过程,得到结论如下:
1)上层土壤电阻率高于下层土壤电阻率环境中,接地棒雷击暂态电位抬升随着距海洋距离的增大而升高,但上层土壤电阻率低于下层土壤电阻率时变化趋势相反。
2)海陆混合环境中,海洋对接地棒暂态电路模型建立存在一定影响,当海洋环境距接地棒距离超过15 m时,可以近似忽略这种影响,且这个临界距离受雷电流波头时间影响不大。
3)随着上层土壤厚度的增加,接地棒暂态电位抬升受上层土壤影响不断增大。

