一种参考节点不确定的无线传感器网络定位方法

代天成

(成都文理学院 信息工程学院，四川 成都 610401)

0 引言

近年来，随着物联网的快速发展，无线通信技术得到了广泛关注。其中，微型低功耗电子设备的无线通信以其优异的性能得到了广泛应用[1-2]。在未来的社会生活及生产中，无论是家庭、办公室、仓库，还是购物中心的每一个设备，都将通过无线传感器网络(Wireless Sensor Network，WSN)连接到互联网[3-4]。在实际应用场景中，WSN面临的一个主要问题是定位问题，如目标跟踪、广域监测和搜索救援等领域，都需要设备的详细及准确的位置信息[5]。

目前，GPS作为以人造地球卫星为基础的高精度无线电导航定位方法，可在全球任何地方以及近地空间为设备提供准确的地理位置及精确的时间信息，是当前应用最广泛、最普遍的设备定位方法之一[6-7]。但GPS信号容易受建筑物、隧道和地形等影响，导致定位精度差、定位不准确等问题，不适用于GPS信号受阻的室内空间或高层建筑[8]。同时，给每台设备都装上GPS系统成本较高，且整体能耗较大，不符合当前节能减排的目标要求。因此，当前迫切需要探索一种新的低能耗的定位方法，以提高设备定位的可靠性、适应性，并提高定位系统的整体性能[9-10]。

随着定位技术的不断发展，围绕WSN定位技术，已逐渐形成了以集中式算法和分布式算法为主的2种核心方法[11]。其中，集中式算法由一个或多个中心设备收集整个网络元素的所有信息，并通过信息处理获取设备位置，但该方法中心设备需要较高的计算能力，能源消耗较大[6]。在分布式算法中，每个设备通过邻近设备的信息计算获取自己的定位信息，传感器网络由若干计算能力较低的处理器和有限容量电池组成，可有效降低系统能耗[12]。

在实际应用中，系统通常由接收到的信号强度(Received Signal Strength， RSS)值或到达时间(Time of Arrival， TOA)测量值计算设备间的距离信息。但实际情况下，由于测量误差，系统往往无法实现准确的距离测量[13]。此外，由于位置估计误差和误差累积现象，所估算的设备位置也不准确。因此，众多专家学者针对当前WSN定位技术存在的问题开展了大量研究。文献[14]提出了一种改进的DV-hop定位方法，可有效提高未知节点的定位精度。文献[15]提出了一种基于交替修正牛顿法的分布式定位算法，可应用于较大规模的WSN。文献[16]提出了一种基于模糊逻辑和向量粒子群优化的混合定位方法，使用极限学习机优化技术实现节点精准定位。文献[17]提出了一种基于压缩感知的融合定位方法，可有效地减少终端异质性带来的误差。文献[18]提出了一种基于果蝇优化算法的WSN节点定位方法，该方法具有收敛速度快、定位精度高等特点，且具有良好的抗误差能力。上述方法大多集中在仅给出距离误差的情况下，获取目标设备的最小位置误差，而实际测量中涉及的相邻设备的位置误差通常被忽略，容易导致误差累积。文献[19]针对节点不确定的WSN定位问题，提出了一种基于参考节点选择模型的蒙特卡罗定位算法，该算法可在节点移动情况下有效实现节点定位，且定位精度和覆盖率较高，但是由于节点的不确定性导致算法时间复杂度较高。文献[20]在WSN定位算法中引入了质点弹簧模型，但是该模型仅针对非测距定位，且传感器网络中各节点的位置均为已知，因此不适用于移动节点的定位。

针对上述WSN定位技术存在的问题，本文提出了一种参考节点不确定的WSN定位方法。该算法利用改进的弹簧质点法(Spring Mass Method，SMM)估计修正的邻近设备位置和目标设备位置，给出了距离误差和位置误差的平衡点，具有良好的噪声鲁棒性；另外，采用精度稀释(Dilution of Precision， DOP)来量化节点位置的不确定性，提高定位精度。

1 问题定义

1.1 条件假设

为便于分析和研究，假设存在一个由多个通信设备组成的分布式网络，并把这些设备称为一个节点。根据节点自身获取位置信息的能力，可将节点分为锚节点和普通节点2类。其中，锚节点可以通过机载GPS或其他方法获得位置信息，普通节点可通过与附近节点交换特定信息来获得位置信息。此外，根据节点在定位过程中所扮演的角色，节点又可以分为参考节点和目标节点。其中，目标节点是在计算过程中待定位的节点。同时，参考节点的位置是已知的，可以支持目标节点的位置定位。

在分布式网络中，若2个节点可以直接或在其他节点协助下交换消息，则称之为连接。此处考虑一个完全连通的网络，且网络中任意2个节点是连接的。此外，若每个节点至少有K个单跳邻居节点，则称之为K连通网络。

所提方法为迭代分布式定位方法，通过位于锚节点附近的节点到位于网络边缘节点的不断迭代估计节点位置，利用每个相邻节点自身的位置信息进行位置估计。

1.2 不确定性分析

由于距离测量误差和算法本身的缺陷，每种定位方法都存在一定的位置估计误差。将量化估计误差称为不确定性。通常，距离不确定性是由测量设备误差和周围环境引起的，而位置的不确定性又取决于距离的不确定性、定位算法的性能和参考节点的空间布局。因此，在大多数定位算法中，都考虑了距离不确定性和目标节点的位置不确定性。但大多数定位方法都假设参考节点的位置是绝对正确的，从而使得参考节点位置的不确定性经常被忽略。因此，分布式定位算法普遍存在参考节点位置误差，如果忽略参考节点位置的不确定性，再通过一个迭代过程进行传播，误差将不会衰减，并持续积累在目标节点位置处。因此，提出了一种考虑参考节点位置不确定性的算法。

本文使用DOP概念来量化位置的不确定性。由于距离误差与位置估计误差之比随参考节点的几何形状变化而变化,因此，位置估计误差可以通过数学建模进行处理。理论上，估计的目标节点位置由3个圆的交点确定，其半径与实测距离相同，中心点为参考节点位置。若没有测量误差，则交点始终存在。然而，在实际应用中由于距离测量误差，交点并不存在。3个圆的其中一条线的粗细是由测量误差的数量决定的，使得3个圆形成一个相交区域，而不是一个相交点，相交区域面积的大小取决于线的粗细和参考节点的几何布局。参考点几何形状、距离测量误差和位置估计误差之间的数学关系如下：

Δx=H-1Δρ，

(1)

式中，Δx∈RND为与二维坐标系中目标节点位置误差ND有关的向量；Δρ为与距离测量误差有关的向量；H为包含Δx和Δρ关系的变换矩阵。若Δx和Δρ的大小不同，则用式(2)代替式(1)：

Δx=(HTH)-1HTΔρ，

(2)

式中，矩阵H由hij组成，hij为：

H=[hij]NRT×ND，

(3)

(4)

式中，NRT为参与目标节点DT定位的引用节点数；矩阵H的元素将根据目标定位中使用的定位算法变化而变化。

根据式(2)可推导出位置误差矢量σp的标准差与测距误差矢量σr的关系：

E[(HTH)-1HTΔρΔρTH(HTH)-1]=

(5)

假设忽略每个测量值之间的相关性。因此，(HTH)-1仅反映几何效应，并成为一个对角矩阵。此时，参考节点位置不确定性经过DOP后如下：

(6)

式中，tr{*}表示求解矩阵的迹。可通过计算DOP来估计目标节点位置的不确定性，该不确定性由参与目标节点定位的参考节点的几何部署决定。DOP的2种分布方式如图1所示。

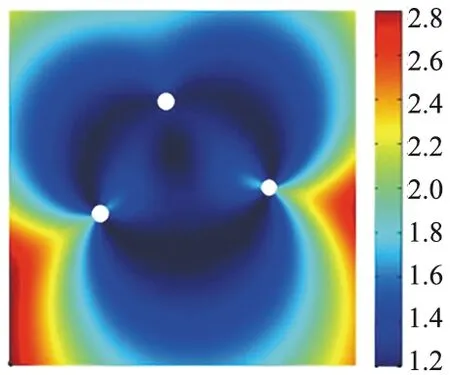
(a) 误差阻性几何形状

2 系统模型构建

2.1 建模方案

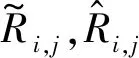
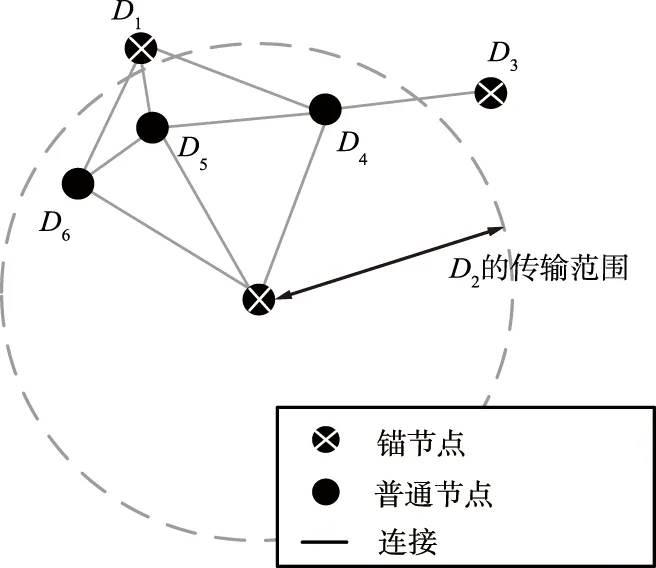
图2 目标系统示例Fig.2 Example of scenario

2.2 弹簧质点法

在节点位置估计过程中，采用了具有简单性和容错性的改进SMM。SMM的逻辑架构如图3所示。由图3可以看出，目标节点和每个参考节点连接在逻辑弹簧上，同时在每个参考节点的目标节点方向上施加逻辑力Fi，该力由弹簧系数和变形长度决定。通过逻辑力Fi的施加，可有效减小测量距离和估计距离之间的差异。其中，估计距离是指估计的目标节点位置和参考节点位置之间的距离。随后，目标节点沿合力方向移动，最终的目标节点位置是逻辑力之和为零的位置，此时每个逻辑弹簧都处于平衡状态。

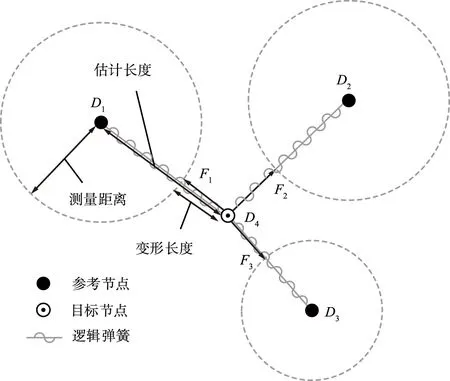
图3 SMM的逻辑架构Fig.3 The conceptual framework of SMM

3 基于位置不确定性的定位方法

3.1 改进的SMM

由上述分析可知，通过使用SMM，可以从粗略估计的初始位置细化目标节点位置。所提方法可以同时处理参考节点的位置不确定性和距离不确定性，还可同时估计更新后的参考节点位置和目标节点的位置。

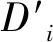
3.2 基于位置不确定性的定位方法

基于位置不确定性的定位方法示意如图4所示。由图4可以看出，每个参考节点和目标节点均朝其作用力方向移动。当所有组件达到平衡状态后，可确定目标节点的位置XDT，且参考节点将其位置更新为平衡点XDi。最后，通过算法的持续递归运行，直到每个节点都计算出其最终位置。

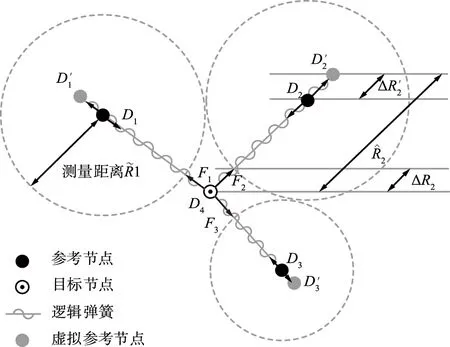
图4 基于位置不确定性的定位方法示意Fig.4 Positioning method based on uncertain positions

所提方法中，平衡状态的数学表达式如下：

(7)

由于作用在参考节点上的2个力的大小是相同的，可得：

ki,jΔRi=ki′,jΔR′i，

(8)

式中，ΔRi为连接目标和参考节点Di之间的逻辑弹簧的扩展长度；ΔR′i为连接Di和D′i之间的逻辑弹簧的扩展长度。

由于弹簧系数ki,j和ki′,j与不确定度成反比，低不确定度值表示测量值或估计值接近实际值，即弹簧的延伸长度较短。因此，将弹簧系数和不确定性之间的关系定义为：

(9)

式中，ωr(σr)，ωp(σp)均为通过位置估计算法改变的权函数，且ωr(σr) =σr，ωp(σp)=σr。定义ΔRi，ΔR′i和估计范围的数学方程：

(10)

通过求解式(8)～式(10)构成的方程组，可将式(7)变换为：

(11)

式中，ui为作用在目标节点上的力的单位向量。在有噪声的情况下，更合理的解决方案是实现最小化的成本函数CT(XDT)：

(12)

式(12)的三维结构示意如图5所示。由图5可以看出，目标节点的位置固定在图的最低点。找到目标节点位置XDT后，参考节点XDi的更新位置可由下式计算：

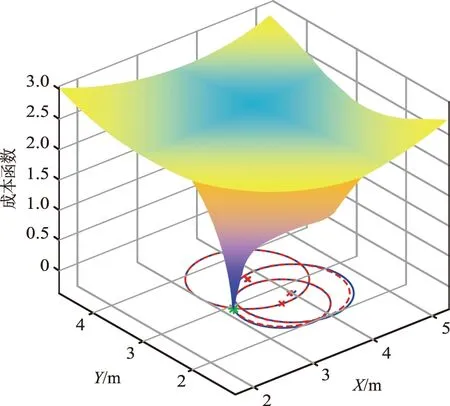
图5 成本函数的三维结构Fig.5 Three-dimensional plot of a cost function

(13)

所提算法的估计结果如图6所示。图6中每个圆的半径表示从参考节点到目标节点的测量距离。结果表明，当估计距离大于测量距离时，参考节点向目标节点移动，反之亦然。

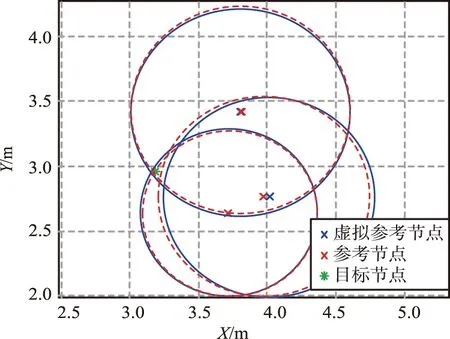
图6 所提算法的估计结果Fig.6 Estimation result of the proposed algorithm

4 仿真分析与实验验证

为了对所提方法的性能进行评估，在Lkm×Lkm的场地内对所提方法进行了仿真分析与实验验证，其中整个节点的数量和锚节点的数量用N和M表示，传输范围用RT表示，每个节点在其传输范围内至少有K个相邻节点。锚节点的数量M由锚节点比例α(0 <α≤1)确定，传输距离RT根据传输距离比β=RT/L确定。将所有与误差有关的参数都根据传输距离RT进行归一化处理，并将路径损耗指数设置为3.5。最后，通过梯度下降法获取成本函数的最小值。

4.1 仿真结果

在4 km×4 km的二维区域进行了仿真分析，令设备总数为N=100，假设给定的网络是三连通网络，并假设整个节点具有相同的传输范围，并且保证了良好的信道互易性，从而使测量误差是正态分布的形式。

将所提算法与不考虑参考节点位置不确定性的SMM进行对比。在Matlab平台上，通过改变噪声比、锚节点比和传输距离比等变量，验证了2种算法的定位性能，仿真结果如下：

① 测量距离噪声比的影响：仿真中将噪声比Ne/RT从5%变化到30%。将锚节点比固定为α=0.1，且传输距离比β为0.2。距离噪声比变化引起的平均位置误差结果如图7所示。由图7可以看出，所提方法的噪声比与位置误差成正相关，且所提方法与SMM的位置误差相比，还能显示相对位置误差。此外，在噪声比变化的情况下，所提方法的平均位置误差比传统SMM降低了76.43%～90.02%。当噪声比降低时，所提算法更加有效，主要是因为噪声比值较低，表明由参考节点位置误差引起的误差比由距离测量误差引起的误差更为严重。因此，在位置误差较大的情况下，所提方法具有更好的性能。

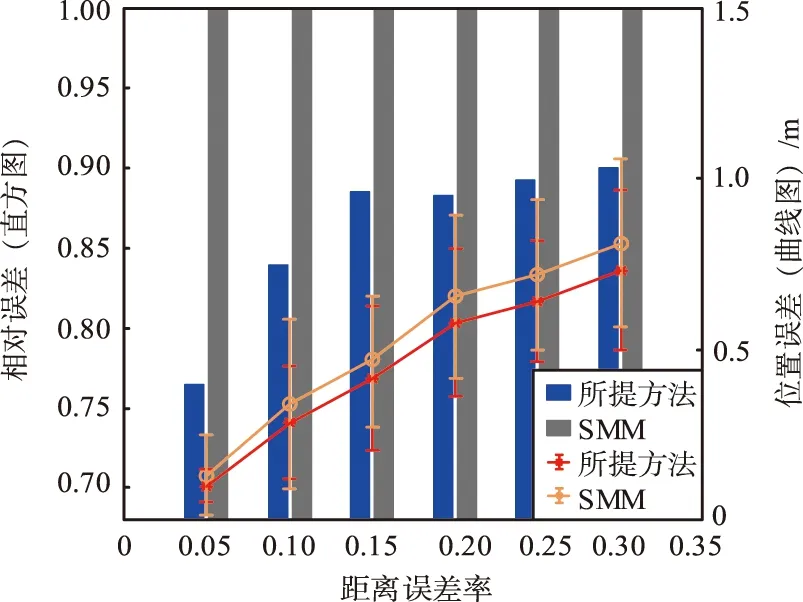
图7 距离噪声比变化引起的平均位置误差结果Fig.7 The average position error caused by the change of the distance-to-noise ratio

② 锚节点比例的影响：仿真实验验证了锚节点比例的影响。将噪声比固定为Ne/RT= 0.4，传输距离固定为β=0.2。锚节点比变化引起的平均位置误差结果如图8所示。由图8可以看出，当锚节点比例α由0.1调整为0.25后，平均位置误差随锚节点比的增大而减小。当锚节点比例较低时，所提方法的性能也能获得明显增益，也就是说即使少量的锚节点在整个网络中引起较大的位置不确定性，所提方法仍能够很好地处理数量稀少的锚节点。在锚节点比例变化的情况下，所提方法的平均位置误差比传统SMM降低了86.79%。

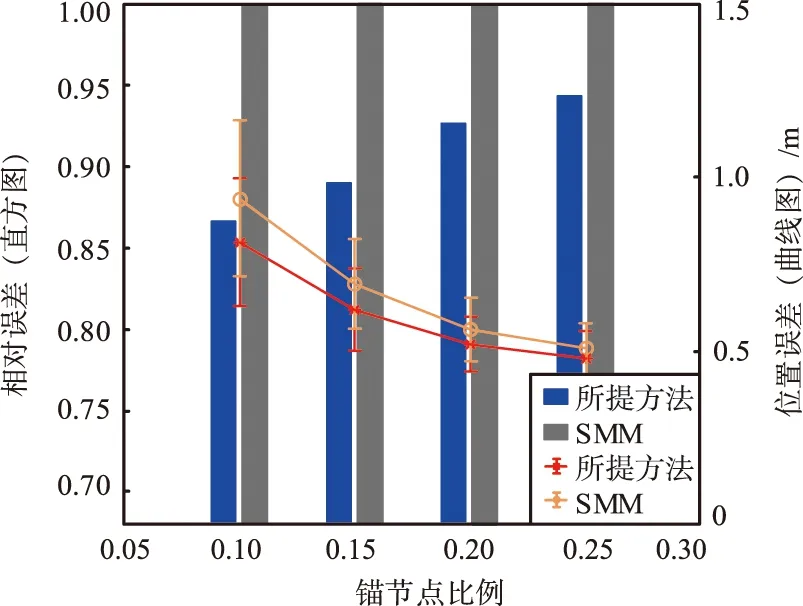
图8 锚节点比变化引起的平均位置误差结果Fig.8 The average position error caused by the change of anchor node ratio

③ 传输距离的影响：通过将传输距离比β从0.2改变至0.35来评估所提方法的性能。锚节点比α设置为0.06，距离噪声比Ne/RT设置为0.2。传输距离比与一次跳跃距离内的节点数有关，即传输距离越远，节点密度就越大。传输距离比变化产生的评估结果如图9所示。由图9可以看出，传输距离的变化不会导致平均位置误差的减小，表明如果存在超过最小数量的节点，则所提方法具有良好的运行性能。

图9 传输距离比变化产生的评估结果Fig.9 Evaluation results produced by changes in the transmission distance ratio

4.2 实验结果

本节将搭建物理实验平台，通过实验验证所提方法的实用性。所搭建的实际环境中使用了基于ZigBee的传输设备，实验在10 m×10 m区域的体育馆内进行，如图10所示。实验区域共布设80个节点，从80个节点中随机选择N个节点，并在不同的节点部署中进行验证。通过测量节点之间的信号强度值，再应用室内路径损耗模型，即可将测量的信号强度值转换为相应的距离。同时，在实验之前，为保障所提方法的可靠性和精度，还需要对每个设备的接收信号功率和辐射模式偏差进行补偿。

图10 实验区域Fig.10 Experiment area

N=60的情况下，所提方法和传统SMM位置估计结果如图11所示。由图11可以看出，所提方法中连接2个点的蓝线的总长度明显短于SMM，这是因为所提方法考虑了参考节点位置的不确定性，因此比SMM具有更好的性能。

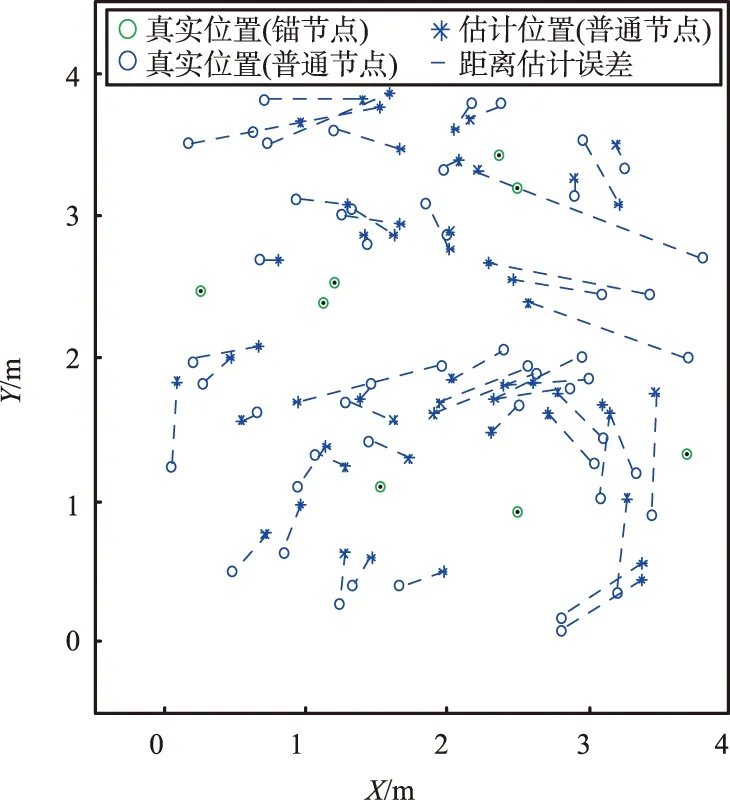
(a) SMM

具体分析如下：

① 锚节点比例的影响：实验在不同锚节点比例的情况下，对所提方法的性能进行了验证。锚节点比例α在0.1～0.25变化，间隔为0.05。锚节点比例变化产生的影响如图12所示。由图12可以看出，实验结果与上文的仿真结果类似，即所提方法可在较高的锚节点比例下产生较低的平均位置误差。仿真结果表明，较低的锚节点比提高所提方法的性能增益，且与传统SMM相比，所提方法的平均位置误差降低了74.57%～93.18%。

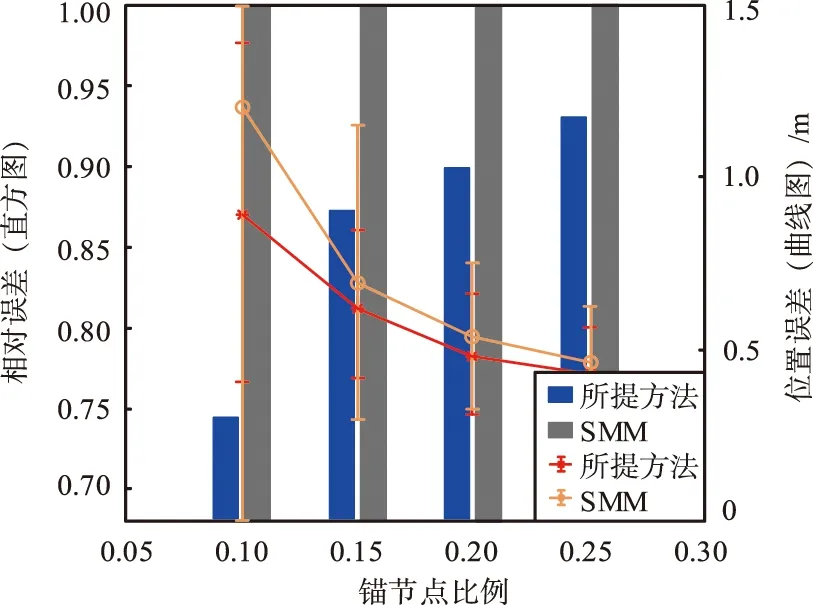
图12 锚节点比变化引起的平均位置误差结果Fig.12 The average position error caused by the change of anchor node ratio

② 传输距离的影响：将传输距离比β由0.25改变至0.31。同时，随着传输距离比的增加，单跳邻居的平均数从9.72增加到15.76。令总节点数N=70，锚节点比例α为0.13。传输距离变化产生的评估结果如图13所示。由图13可以看出，与仿真情况相比，所提方法可通过增加传输距离比来减小平均位置误差。主要因为仿真分析中假定的固定距离噪声比不适用于实际实验，且当用于测量的设备确定后，发生的定位误差是固定的。

由于图13中的平均误差被归一化为传输距离RT，因此平均误差随传输距离比的增加而反向减小。通过消除这种现象并分析非归一化平均误差，即使传输距离比发生变化，平均误差也可保持不变。也就是说，即使功率消耗越大，为了扩展传输范围和收集更多的单跳邻居，平均误差的数量几乎保持不变。实验结果表明，在满足最小准则的情况下，所提方法具有良好的性能，且该性能与传输距离没有直接关系。

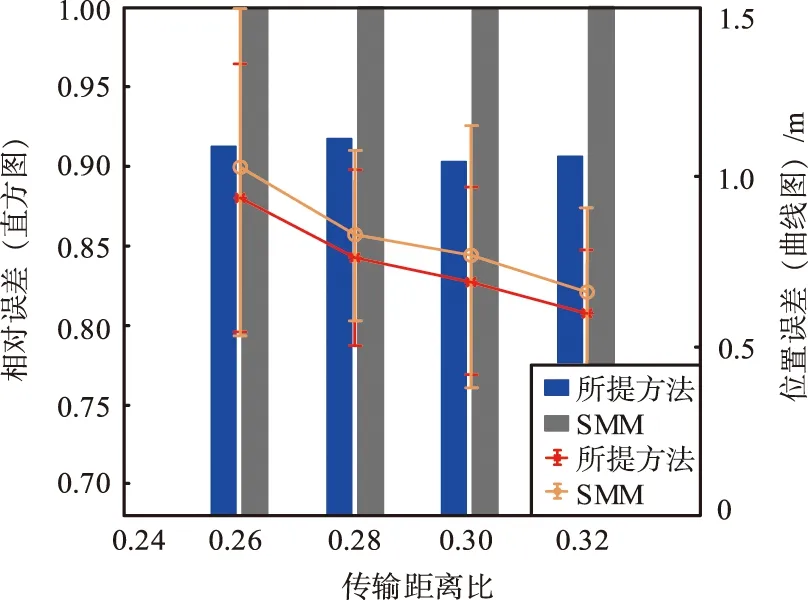
图13 传输距离比变化产生的评估结果Fig.13 Evaluation results produced by changes in the transmission distance ratio

③ 节点部署模式的影响：实验在C形、O形和随机节点部署3种方式下进行。其中，节点数N为60，锚节点比为0.15，单跳相邻节点的平均数分别为13.56，13.47和13.57。在上述3种情况下，与传统SMM相比所提方法的平均位置误差分别为92.9%，94.8%和86.5%。所提方法的相对位置误差结果如图14所示。由图14可以看出，所提方法在C形和O形部署情况下具有相似的定位性能，但在随机部署情况下的性能最佳。

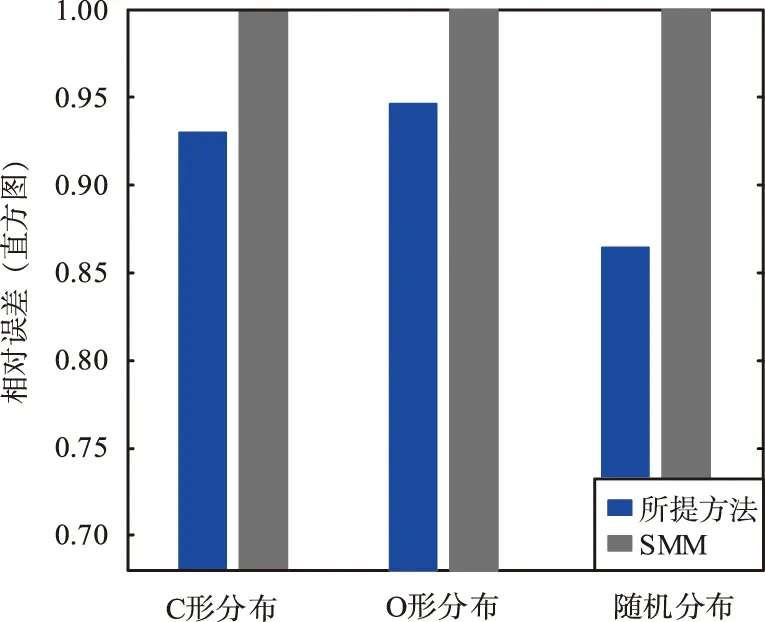
图14 不同节点部署方式的相对位置误差Fig.14 Relative position error under various node deployment modes

不同节点部署方式的位置定位结果如图15所示。节点的初始部署方式如图15(a)和图15(d)所示。所提方法的估计结果如图15(c)和图15(f)所示，传统SMM的估计结果如图15(b)和图15(e)所示。通常，若节点分布不规则，会降低定位精度，此时定位算法无法按预期方式运行。由图15可以看出，即使节点为不规则部署方式，所提方法也具有良好性能，表示位置误差量的蓝线总长度仍小于SMM。此外，在所提算法下，节点连接状态的失真明显降低，总体性能均优于弹簧质点算法。

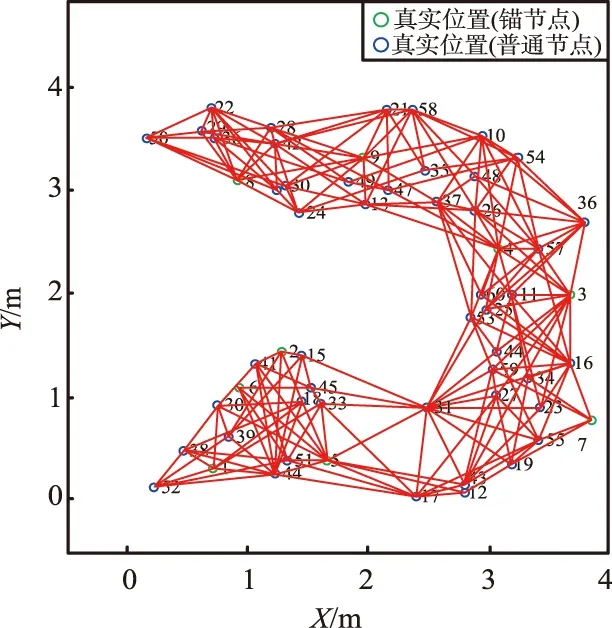
(a) 初始C形部署方式估计结果

5 结束语

针对WSN室内定位问题，提出了一种参考节点不确定的WSN定位方法，并通过仿真分析与实验验证得出以下结论：

① 所提方法可以同时处理参考节点的位置不确定性和距离不确定性，实现了距离误差和位置误差之间的平衡，可有效提高位置估计的精度。

② 所提方法在不同节点部署方式下均具有优越性能，且所提方法的性能与传输距离没有直接关系，并具有良好的噪声鲁棒性。

③ 与传统的SMM相比，所提方法具有明显的性能优势，其平均定位误差相比SMM可降低约75%以上。

此传感器节点的定位实验主要是在室内环境下进行，未考虑其他干扰因素的影响，后续将重点研究该方法的抗干扰性。