基于改进蚁群算法的自动驾驶路径规划研究
绳红强,黄海英,石小锐,崔毅刚
(1. 中国重汽集团济南动力有限公司,山东 济南 250101;2. 武汉大学 数学与统计院,湖北 武汉 430072;3. 山东圣翰财贸职业学院,山东 济南 250316)
0 引言
路径规划是自动驾驶车辆运动控制的关键技术,通常被描述为自动驾驶车辆在空间环境约束下寻找一条从起始点通往目标点的最优无碰撞路径[1]。自动驾驶车辆又称为轮式移动机器人,其路径规划算法的研究源自机器人技术。迄今为止,国内外学者提出了诸多经典的路径规划算法[2-4],如蚁群算法、Dijastra算法、A*算法、粒子群算法、快速探索随机树算法(RRT)、人工势场法、禁忌搜索算法、神经网络法、动态窗口算法等。目前大多数算法针对具体问题需要进行优化整合,自动驾驶车辆安全行驶要求延时必须控制在毫秒甚至微秒级别,对算法效率、规划路径质量提出了较高的要求。
蚁群算法由意大利学者DORIGO M等于1996年首先提出[5],它源于对蚂蚁群体觅食机制的研究。蚁群算法具有自组织、分布式、正反馈、鲁棒性强等优点,易于与其他优化算法相结合,已经广泛用于求解车辆路径规划、机器人路径规划、无人机飞行路径规划等问题[6-13]。但是,蚁群算法理论模型缺乏坚实的数学基础,其关键参数的选择多依靠试验和经验来确定,易出现路径拐点多、转弯角度大、收敛速度慢、局部收敛、搜索停滞等典型问题[14]。
针对蚁群算法的不足,本文提出一种适用于自动驾驶路径规划的改进蚁群算法,以提高规划路径的质量和算法性能,对实现自动驾驶车辆安全行驶具有重要价值。
1 蚁群算法的基本模型
由于蚁群算法原理在DORIGO M等的著作已有详尽的描述,在此不做赘述。下面简要说明蚁群算法的基本数学模型和实现过程的关键步骤。蚁群算法的核心是利用状态转移概率和遗留的信息素浓度实现路径选择。
1.1 状态转移概率
定义蚂蚁在t时刻由节点i转移至节点j的状态转移概率为
(1)
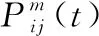
启发函数ηij(t)表达式为
ηij(t)=1/dij
(2)
式中dij为节点i和j的距离,即
1.2 信息素更新规则
当M只蚂蚁完成一次循环后,需对路径信息素更新,其更新公式为
τij(t)=(1-ρ)·τij(t-1)+Δτij
(3)
(4)
式中:τij(t)为t时刻节点i到相邻节点j的路径之间信息素浓度;τij(t-1)为在t-1时刻节点i到相邻节点j的路径之间信息素浓度;ρ为信息素挥发系数,ρ∈(0,1);Δτij为在t-1时刻到t时刻节点i到相邻节点j的路径之间信息素浓度的增量。
1.3 信息素增量更新模型
根据信息素浓度的增量更新方式的不同,DORIGO M等提出3种不同的基本更新模型,分别称之为Ant-Density System(ADS)、Ant-Quantity System (AQS)和Ant-Cycle System (ACS)模型。
若第m只蚂蚁当前循环经过路径(i,j)节点的集合为X{(i,j)|i=1,2,…,n;j=1,2,…,n},则:
ADS模型:
(5)
AQS模型:
(6)
ACS模型:
(7)
式中:Q为信息素强度,影响算法求解速度,为>0的常数;Lm为第m只蚂蚁在本次循环中所走路径的总距离。
上述3个模型的差别:ADS模型和AQS模型采用的是局部更新策略,即蚂蚁每走一步都要更新残留信息素的浓度;ACS模型采用的是全局更新策略,即蚂蚁完成一个循环后再更新残留信息素的浓度,在求解路径规划问题中最为常用,因此ACS模型通常作为信息素更新的基本模型。
2 蚁群算法设计改进
2.1 全局启发函数设计
式(2)中启发函数ηij(t)仅利用了相邻节点的信息,启发性不足,缺乏全局性,易出现规划路径拐点多、角度大、盲目搜索、收敛速度慢[14-15]等问题。本文利用相邻节点和目标点的信息引入贝塞耳平滑曲线函数,构造了一种全局启发函数。
n+1个顶点的n次贝塞耳曲线表达式为
(8)
式中:Pi(i=0,1,2,…,n)为各顶点的位置向量;Bi,n(t)为伯恩斯坦基函数。
(9)
令ηij(t)=P(t),P0=1/dij和P1=1/djE,按贝塞耳曲线函数一阶展开,即取n=1,则
全局启发函数ηij(t)表达式为
(10)
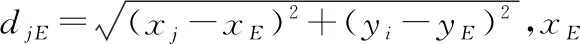
t的大小取决于车速、相邻节点之间的距离。当车辆均速行驶时,t≈dij/(dij+djE)。当djE≫dij时,t→0,则全局启发函数ηij(t)表达式可近似为
(11)
2.2 信息素更新策略
本文提出利用蚂蚁当前路径、最优路径、最差路径和理想路径,构建一种动态调整的信息素增量模型。该信息素增量模型表达式如下:
(12)
式中:n为第n次迭代;Ln,m为当前路径距离,即第m只蚂蚁产生的路径的距离;Lmin为最优路径距离,即第n次迭代产生的最短路径距离;Lmax为最差路径距离,即第n次迭代产生的最长路径距离;Lidv为理想路径距离,即起始点与目标点的直线距离;δ为最优路径距离与最差路径的差值,即δ=Lmax-Ln,m;ε为第n次迭代可接受路径误差,ε值为一常数。
在迭代过程中,新的信息素增量机制可以自适应动态调整信息素的强度,使优化过程加速向全局最优路径收敛。当δ>ε时,Lmax与Ln,m差值越大,信息素强度越大,全局收敛时间缩短,算法求解效率得到提升;当δ≤ε时,Ln,m与Lmin越接近,信息素浓度蒸发越快,使算法避免出现过早收敛陷入局部最优。Lidv在迭代过程中起到参照作用,可作为最佳路径决策依据。
2.3 算法过程
根据上述理论,按照本文提出的全局启发函数和信息素更新策略,自动驾驶车辆路径规划算法流程如图1所示,步骤如下所述。

图1 本文算法流程图
步骤1:获取环境地图数据。定位起始点S和目标点E;获取空间所有节点信息,计算邻接矩阵D和计算启发式信息矩阵。
步骤2:参数初始化。初始化迭代次数N,蚂蚁规模M,信息启发式因子α,期望启发式因子β,信息素挥发系数ρ,信息素浓度ε、t,当前路径列表RT,禁忌表TS。将起始点S置于禁忌表RT和当前路径列表TS。

步骤4:蚂蚁序号更新。若第m只蚂蚁的当前路径列表包含了目标点或无路径且m≥M,则转入步骤5,否则返回步骤3。
步骤5:信息素更新。计算当前迭代最优路径并按式(3)和式(12)更新信息素矩阵。
步骤6:迭代或停止。若n≥N,则输出最优路径并停止迭代,否则返回步骤3。
3 仿真实验与分析
3.1 仿真环境搭建
经典的环境地图建模方法有栅格法、几何法、可视图法等[16-17]。
栅格法是将自动驾驶车辆行驶的空间分解成一系列具有二值信息的网格单元。栅格法表达简单,易于实现,在路径规划中最为常用。
下面以10×10二维栅格地图为例,简要说明栅格地图数学模型和表示形式,如图2所示。
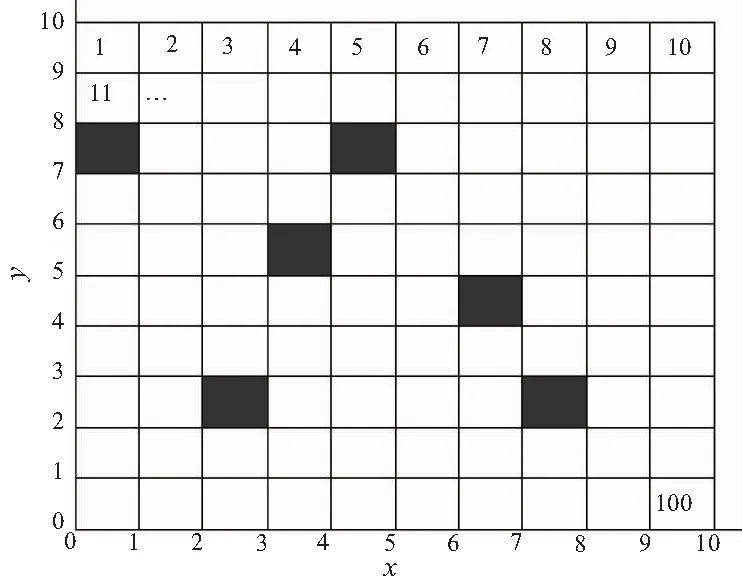
图2 10×10二维栅格地图
图2中黑色栅格表示障碍物,白色栅格是自由栅格。设每个栅格的中心坐标为栅格的直角坐标,每个栅格编号与直角坐标一一对应,则栅格地图中任意一点的坐标(xi,yi)与栅格编号i的映射关系如下所示。
xi=a·[mod(i,MM)-0.5]
(13)
yi=a·[MM+0.5-ceil(i/MM)]
(14)
式中:a为每个栅格边长;MM为横坐标的最大栅格数值;mod(a,b)为(a/b)取余结果;ceil函数为朝正无穷大方向取整。
在栅格地图中,在当前节点i位置路径决策可选方向有“十”字型或“米”字型[18]。本文采用“米”字型方向选择规则,如图3所示。
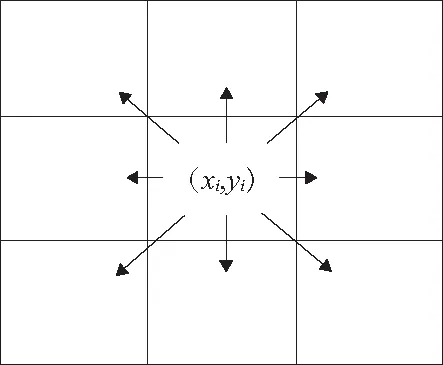
图3 可行路径方向图
3.2 结果与分析
通过仿真程序,下面对本文算法的有效性在栅格地图环境下进行试验验证。仿真环境如图4所示的20×20二维栅格地图。
仿真试验参数设置详见表1,仿真试验结果如图4、图5和表2所示。

表1 仿真实验参数设置

图4 算法路径规划图
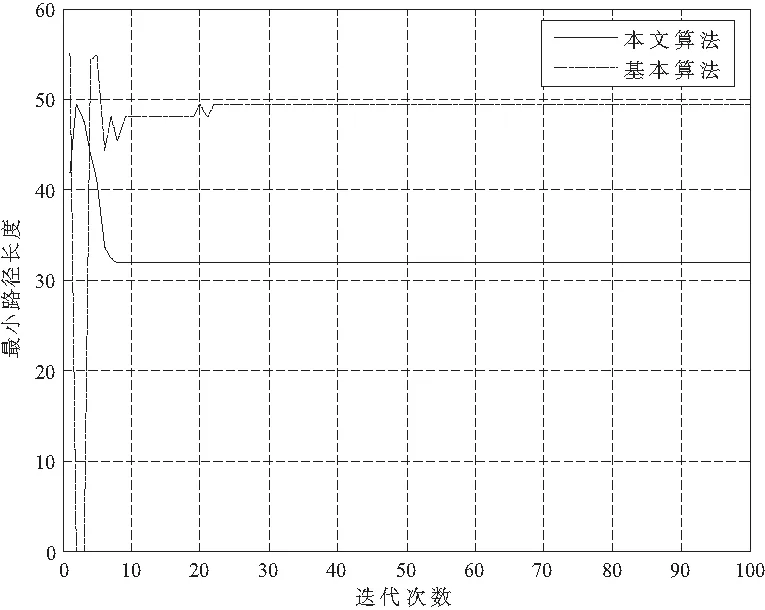
图5 算法收敛变化曲线

表2 仿真实验结果
由图4可见,本文改进算法可以实现自动驾驶车辆在复杂的障碍环境中寻找到一条从起始节点出发到达目标点的无碰撞最优路径。
由图5和表2结果显示,本文算法迭代8次达到收敛,规划路径距离为31.799,明显优于基本算法。本文算法全路径拐点有19个,拐角之和为900°,其中45°拐角18次、90°拐角1次;而基本算法的拐点数为27次,拐角之和为2 170°,其中直角拐角有21次,45°拐角6次,显然本文算法规划路径更平滑。
4 结语
本文提出一种用于自动驾驶路径规划的改进蚁群算法。仿真实验结果表明:本文构造的全局启发函数,在引导蚂蚁对目标节点的感知、消除路径搜索的盲目性和改善规划路径的平滑性方面效果显著;提出的基于动态调整的信息素更新策略,使算法优化过程自适应调整信息素的强度,全局收敛速度得到明显提升。
未来进一步探索建立基于自动驾驶车辆完整约束条件的精确算法模型,提高算法的效率和稳健性,满足复杂环境下实时规避碰撞风险将是自动驾驶路径规划研究的重点问题。

