基于Weibull分布函数的厨余垃圾干燥过程模拟研究

鲍安红， 豆玉婷， 彭和， 刘柯伶

西南大学 工程技术学院， 重庆 400715

厨余垃圾来源于家庭、 学校食堂、 餐饮行业等， 全国每年产生量约为9 000万t， 在人口密集的一线城市， 厨余垃圾的增长速率约为10%[1]， 其含有大量的水分， 易腐烂变质、 滋生细菌， 若不处理会影响人体健康和造成环境污染． 厨余垃圾的主要成分包括淀粉、 蛋白质、 纤维素、 油脂等， 其成分复杂， 如何实现厨余垃圾的无害化、 减量化和资源化处理已经成为社会广泛关注的热点问题[2]．

已有研究利用厨余垃圾的发酵功能和好氧堆肥技术将其制作成有机肥， 这种技术简单、 易推广， 但同时存在着堆肥品质难控制、 成本高、 占地面积大等缺点[3]． 而采用厌氧消化处理厨余垃圾是一种环境友好的方式， 但单独对厨余垃圾进行厌氧消化处理， 会出现脂肪酸堆积现象， 降低系统pH值， 导致厌氧消化产气量降低， 即使利用粪便、 污泥或其他生物质与其进行联合厌氧消化处理可以得到改善， 但仍需精准控制厌氧消化过程中的温度、 pH值、 TS(总固体)体积分数等影响因素， 技术含量高[4]． 相比之下， 干燥厨余垃圾蒸发其水分， 降低微生物存活的可能性， 既能减少滋生细菌污染环境和危害人体健康[5]， 又便于后续对其进行有效处理和再利用， 如对厨余垃圾干燥预处理后， 可以通过热解手段生产焦炭、 焦油和燃气等能源材料[6]． 可见， 开展厨余垃圾干燥处理研究， 对推动厨余垃圾的资源化再利用有重要的经济、 社会效益．

Weibull分布函数可以很容易地推导出数值分布参数， 适用性广、 具有很好的兼容性， 常应用于物料干燥水分比曲线拟合， 以表征物料的干燥动力学行为[7]． 薛广等[8]在罗非鱼片真空微波干燥试验时比较多种数学模型， 得出Weibull模型相比Page等其他模型拟合度更高． 物料的干燥方式有喷雾干燥、 红外干燥等， 食品干燥多采用热风干燥技术[9]， 而利用Weibull模型模拟研究厨余垃圾热风干燥过程及其适用性鲜有报道．

为此， 本文对厨余垃圾在不同干燥温度和不同铺设厚度下的干燥过程进行分析， 并采用Weibull分布函数模拟厨余垃圾干燥过程预测模型， 验证模型对厨余垃圾干燥过程的拟合度， 探究和阐述模型中各参数的影响因素以及物理意义， 以期为探索更优的厨余垃圾干燥处理工艺提供试验依据．

1 材料与方法

1.1 试验材料

试验中所用的厨余垃圾取自西南大学竹园学生食堂， 为学生饭后余下的剩菜、 剩饭， 其组成部分有米饭、 蛋类、 蔬菜和肉类， 去除骨头等杂物， 采用烘干法测得厨余垃圾的初始湿基含水率为60%～69%．

1.2 试验方法

将1.1中收取的厨余垃圾均匀地铺设于3个相同的标准筛中(均为60目)， 标准筛高度均为4.2 cm． 对于食品、 药材类的干燥， 物料的厚度一般为1～10 mm， 考虑到大规模处理厨余垃圾的实际情况， 需要增加物料的铺设厚度以提高处理效率， 参考荞麦干燥过程并结合标准筛的高度， 试验时筛内物料厚度分别取1.4，2.8，4.2 cm[10-12]． 选用DHG-9245A型电热鼓风干燥箱(上海一恒科学仪器有限公司)对样品进行干燥， 干燥温度分别设定为75 ℃，90 ℃和105 ℃， 风速恒定为1 m/s． 干燥箱预热至指定温度， 对样品称质量后放入干燥箱进行干燥， 此后每隔30 min称质量1次． 根据《油料 水分及挥发物含量测定》(GB/T 14489.1-2008)， 直到相邻两次质量的差值与初始质量之比小于0.1%时则认为物料完全干燥[13]， 即停止试验．

1.3 Weibull分布函数模型

水分比表示物料在一定干燥条件下干燥时物料所含水分的变化， 用MR表示， 干燥过程中不同时刻的厨余垃圾的水分比计算公式如公式(1)所示[14]：

(1)

式中，M0，Mt和Me分别表示厨余垃圾在干燥起始、 任意时刻t以及达到平衡时的干基含水率， g/g．

干燥速率表示物料干燥时水分含量变化的快慢， 用DR表示， 计算公式如公式(2)所示[15]：

(2)

式中，Mt1和Mt2分别表示厨余垃圾在干燥过程中t1和t2时刻的干基含水率， g/g．

Weibull分布函数由公式(3)表示[16]：

(3)

式中，t为干燥时间， min； 尺度参数α表示干燥的速率常数， min， 其值大约等于干燥过程完成63%时所用的时间； 形状参数β与干燥初期物料的传质速率有关， 无量纲数，β值越小， 说明干燥初期的干燥速率越大．

Weibull分布函数对厨余垃圾干燥试验的数据进行拟合时， 采用非线性回归分析． 模型拟合的优劣程度由相关系数R2、 均方根误差RMSE(用RMSE表示)以及离差平方和x2来评价，R2值越大、RMSE和x2值越小， 模型拟合得越好． 这3个指标的计算公式如式(4)-式(6)所示[17]． 模型的拟合过程在软件Origin 2017上完成．

(4)

(5)

(6)

式中，MRexp，i为试验实测的第i个水分比，MRpre，i为模型预测的第i个水分比；N为试验测得的数据个数；z为常数的个数．

1.4 有效水分扩散系数

有效水分扩散系数是表示干燥过程中水分扩散速度的动态量， 是衡量物料水分在分子扩散、 毛细管流、 收缩变形和吸水动力学流等因素共同作用下的迁移特点的物理参数[18-19]． 其计算公式根据Fick第二定律简化所得， 如式(7)所示[20]：

(7)

式中，Deff为有效水分扩散系数， m2/s；L为物料厚度的一半， m；t为时间， s．

Weibull分布函数可以不被物料水分迁移方式所制约， 能够近似地估算Dcal， 即估算水分有效扩散系数， 其计算如式(8)所示[19]：

(8)

式中，r为物料体积等效半径， m．

Deff与Dcal之间的数学表达式如式(9) 所示[19]：

(9)

式中，Rg为物料的几何参数．

1.5 干燥活化能(Ea)

干燥活化能(Ea)表示干燥物料时脱去单位水分所需要消耗的能量， 它的值越大， 表示物料干燥越困难， 干燥消耗的能量越大[20-21]． 干燥活化能Ea按式(10)计算[22]：

(10)

式中，Ea为干燥活化能， kJ/mol；D0为物料的扩散基数， 定值， m2/s；T为物料的干燥温度， ℃；R为气体摩尔常数， 其值为8.314×10-3kJ/(mol·K)．

将式(9)带入式(10)并取对数得：

(11)

2 试验结果

2.1 干燥动力曲线

2.1.1 厚度对厨余垃圾干燥动力曲线的影响

以温度为90 ℃时的试验结果为例， 得到不同铺设厚度物料的干燥曲线如图1所示．

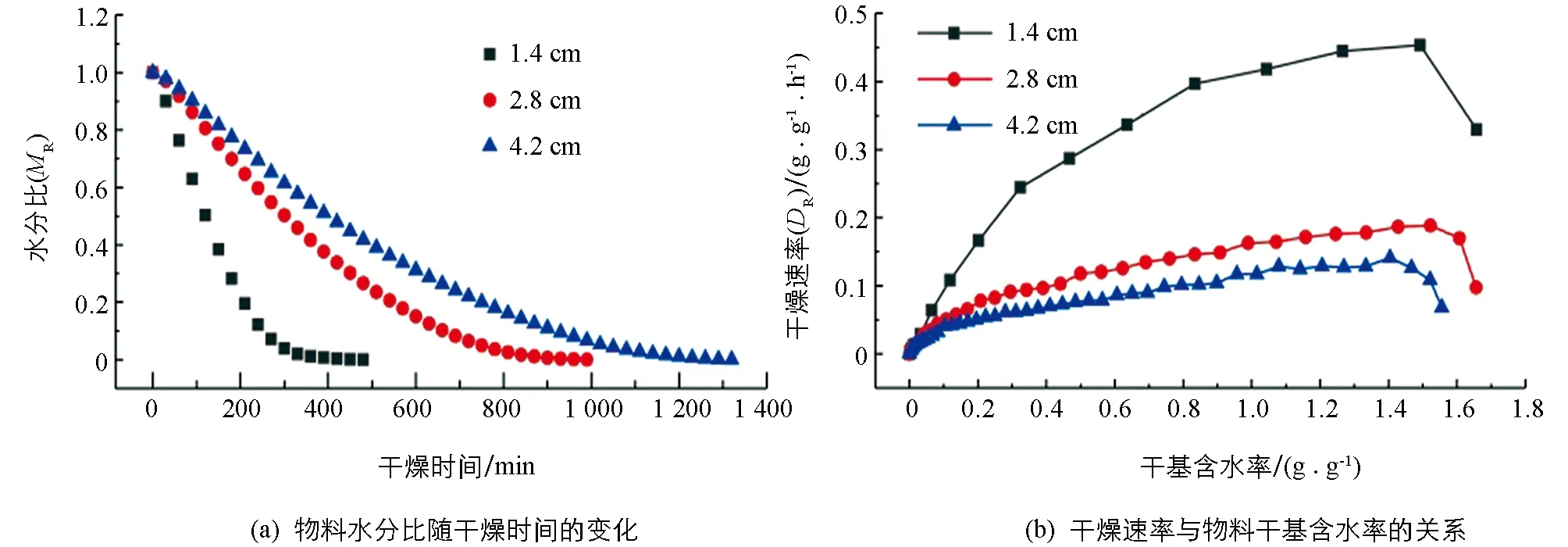
图1 90 ℃下不同铺设厚度物料干燥过程

由图1(a)可知， 1.4，2.8，4.2 cm厚的厨余垃圾干燥完成所用的时间分别为480，990，1 320 min． 1.4 cm厚物料干燥耗时比2.8 cm厚物料缩短了106.3%， 2.8 cm厚物料干燥耗时比4.2 cm厚物料缩短了33.3%． 相同干燥温度下厨余垃圾完全干燥所需的时间随着厚度的增加而增加， 原因在于物料越薄其单位体积的分子接受到的能量越多， 水分子汽化速率越大， 完全干燥所需时间越短． 且物料干燥后体积收缩， 物料间间隙扩张， 最终形成贯通通道， 使得厚度薄的物料与热空气的相对接触面积更大， 便于水分蒸出， 干燥时间缩短． 对于干燥速率， 由图1(b)可知， 不同厚度的厨余垃圾都存在先升速再降速的干燥过程， 但厚度越小， 在干燥全过程中的干燥速率就越大， 干燥速率变化也越明显． 由此可知， 减小物料铺设厚度可以有效缩短干燥时间， 提高效率． 3种不同铺设厚度的物料干燥速率最大时的干基含水率皆处于1.4～1.6 g/g之间， 在此之前整体处于干燥速率上升状态， 而后发生陡降． 此外， 铺设厚度为1.4 cm的物料干燥速率显著大于厚度为2.8 cm和4.2 cm的物料干燥速率， 而后两者的干燥速率相对接近．

2.1.2 干燥温度对厨余垃圾干燥动力曲线的影响

对2.8 cm厚度的厨余垃圾的烘干结果进行分析， 得到不同温度下干燥特征曲线如图2所示． 结果表明， 物料的干燥速率随着干燥温度的升高而升高， 厨余垃圾所需的干燥时间随着温度升高而缩短． 如图2(a)所示， 干燥温度为75 ℃，90 ℃和105 ℃时， 物料完全干燥的耗时分别为1 200，990，840 min， 105 ℃下的干燥时间分别比在75 ℃和90 ℃下缩短了42.9%和15.2%． 由图2(b)可知， 各温度下试样的干燥过程均呈现出先升速干燥后降速干燥的特点． 3种温度下干燥速率最大时的干基含水率皆处于1.4～1.7 g/g之间， 在此之前整体处于干燥速率上升状态， 而后发生陡降． 在干燥初期， 厨余垃圾的水分转化为水蒸汽排到外界需要时间， 干燥速率较低， 但烘箱内干燥升温很快， 厨余垃圾的干燥速率上升很快． 在干燥中期， 厨余垃圾吸收烘箱加热带来的热量， 流失了绝大部分的水分， 干燥速率趋于稳定． 在干燥后期， 厨余垃圾排出的水分散失到烘箱外， 物料的含水率降到一定程度， 自由水挥发减少， 剩下难以挥发的结合水， 干燥速率逐渐减小， 这与陈梅倩等[23]的结论相似．

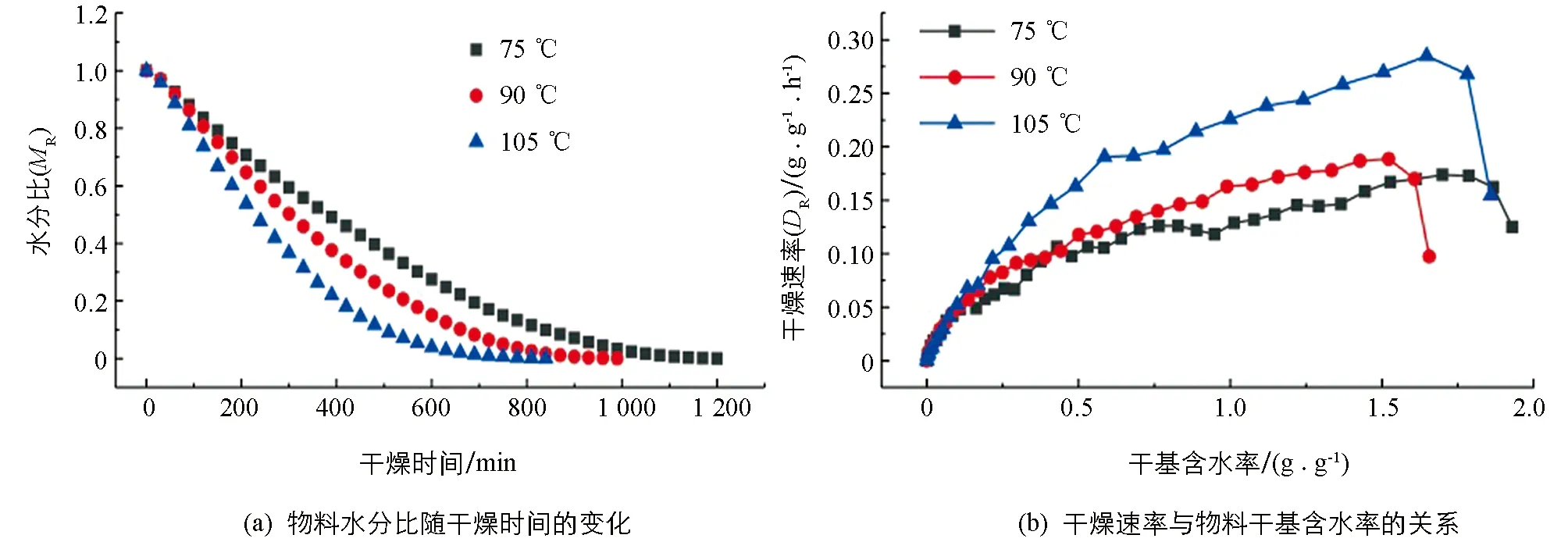
图2 铺设厚度为2.8 cm的物料在不同干燥温度下的干燥过程

2.2 干燥曲线的Weibull分布函数模型

2.2.1 尺度参数α的物理意义及影响因素

运用Weibull分布函数对厨余垃圾的干燥曲线进行拟合， 拟合结果见表1． 由表可见， 相关系数R2在0.995～0.999区间内， 离差平方和x2在1.54×10-4～5.16×10-4之间， 均方根误差RMSE在1.17×10-2～2.21×10-2之间． 从这3个评价指标结果可看出， Weibull分布函数对厨余垃圾的热风干燥曲线的拟合程度较高， 为后续分析厨余垃圾的干燥过程提供了基础条件．

尺度参数α表示干燥过程的速率常数， 其值大约为干燥过程完成63%所需要的时间． 从表1可见， 相同铺设厚度的厨余垃圾随着干燥温度(75 ℃，90 ℃，105 ℃)的提升， 厨余垃圾的尺度参数α分别由247.381减小到139.941， 480.096减小到288.484， 716.061减小到402.215； 同一温度的厨余垃圾随着厚度的增加(1.4，2.8，4.2 cm)， 厨余垃圾的尺度参数α分别由247.381增大到716.061， 150.223增大到515.796， 139.941增大到402.215．

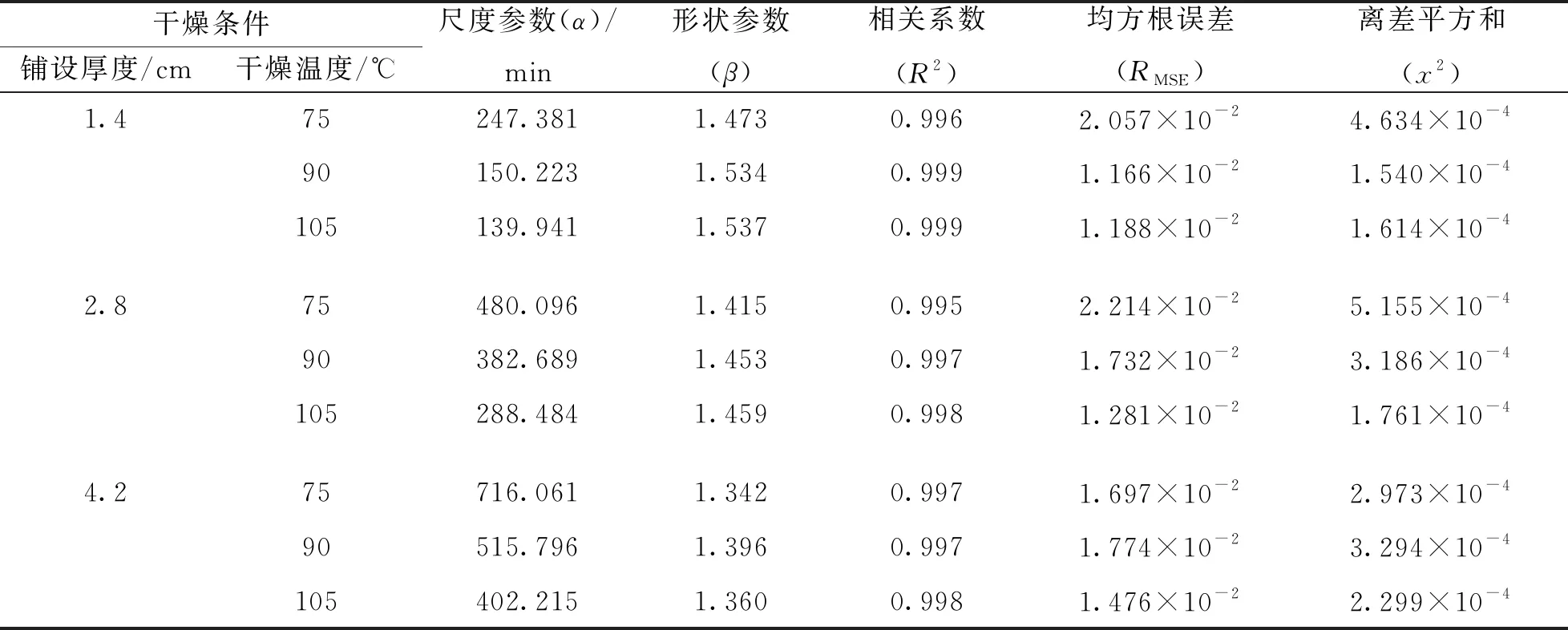
表1 Weibull分布函数对厨余垃圾干燥过程中物料水分比随干燥时间变化曲线的拟合结果

由此可见， 对同一干燥物料来说， 干燥温度和铺设厚度显著影响尺度参数α． 影响特征表现为： 在相同厚度下， 尺度参数α随着干燥温度的升高而减小， 在相同温度下， 尺度参数α随着干燥厚度的增加而增加．

2.2.2 形状参数β的物理意义以及影响因素

形状参数β与干燥过程中水分的迁移机理有关． 由表1可知，β的取值范围为1.342～1.537， 理论上干燥过程存在短暂的升速干燥阶段， 而后为内部水分控制下的降速干燥过程． 在干燥开始初期， 由于外部水尚未完全干燥， 外部水分随干燥进行而减少， 则单位质量水所接受到的热量越高， 干燥就加快， 表现为升速干燥阶段． 而当外部水完全干燥后， 后续水分损失为蕴藏在物料内部水的干燥引起， 内部水的蒸发干燥相比外部水显然更加困难， 需要更高的能量和蒸发时间， 故干燥速率减小， 表现为降速干燥． 由于升速阶段短暂以及忽略试验中称量物料产生的误差影响， 干燥速率曲线主要呈现降速干燥过程， 不同干燥条件下的β无明显区别． 类似的结论在罗非鱼、 猕猴桃片和香菇的干燥中也有出现[8-10，24]．

2.3 有效水分扩散系数

厨余垃圾的整个干燥过程先升速干燥再降速干燥， 不满足Fick第二定律即要求物料在干燥时要全程处于降速干燥阶段的限制条件． 而Weibull分布函数不受该条件的影响， 可利用该函数有效估算厨余垃圾的水分扩散系数． 根据公式(7)可知厨余垃圾的水分比(MR)的自然对数lnMR与干燥时间t呈线性关系， 由线性回归计算得出厨余垃圾的有效水分扩散系数(Deff)， 结合公式(8)和公式(9)求得不同干燥条件下厨余垃圾的估算水分扩散系数和几何参数， 计算结果如表2所示．

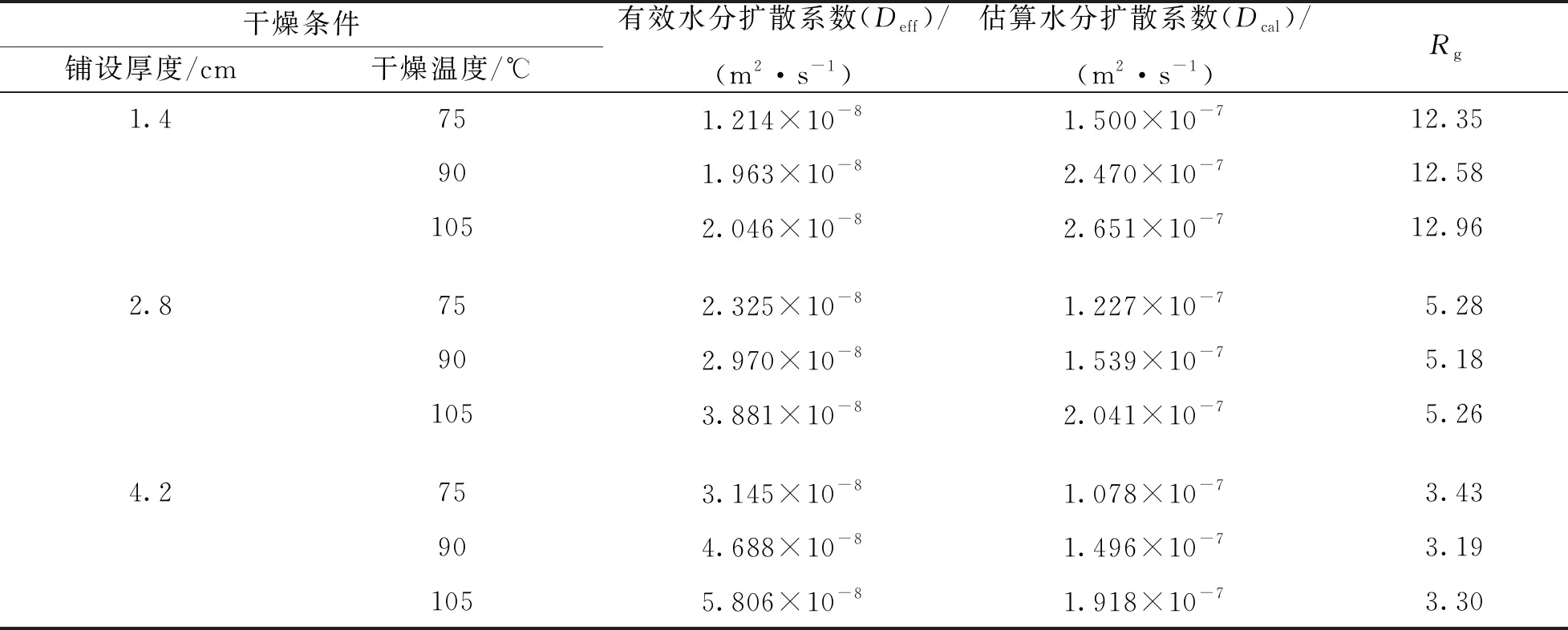
表2 不同干燥条件下厨余垃圾的有效水分扩散系数

由表2可知， 相同物料铺设厚度下的几何参数(Rg)波动很小， 而不同铺设厚度下的几何参数差异明显． 这是由于厨余垃圾在干燥过程中持续脱水， 物料整体出现了收缩变形导致Rg发生变化， 这也证实了物料干燥时的几何尺度对Rg影响显著． 有效水分扩散系数(Deff)和估算有效水分扩散系数(Dcal)均与干燥温度正相关， 这是因为提高干燥温度可以使物料水分子能量增加， 加剧物料分子运动速度， 从而增大物料的分子扩散速率． 表中数据还显示Dcal随着物料厚度的增加而减小， 与业内研究学者所得结论基本一致[25]． 而Deff随着物料厚度的增加而增加， 有违一般规律， 这可能是由于采用Fick第二定律对其进行计算时没有考虑物料收缩．

2.4 干燥活化能

公式(11)显示， lnDcal与1/(T+273.15)呈线性关系， 线性拟合计算结果如图3所示． 通过对拟合结果进行计算得到物料的干燥活化能． 1.4 cm厚厨余垃圾的干燥活化能为20.99 kJ/mol， 2.8 cm厚厨余垃圾的干燥活化能为18.55 kJ/mol， 4.2 cm厚厨余垃圾的干燥活化能为21.07 kJ/mol． 2.8 cm厚物料组的数值比其他两组的结果小， 说明适中的厨余垃圾厚度干燥较为容易．

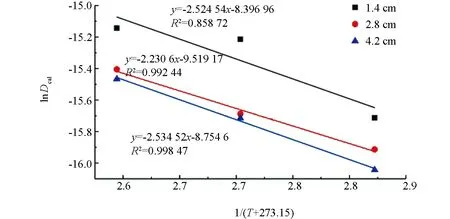
图3 不同铺设厚度下估算有效水分扩散系数Dcal与干燥温度T的相关关系， R2为相关系数

3 结论

1) 可能存在使物料干燥速率发生较大变化的临界铺设厚度(1.4～2.8 cm)和临界干燥温度(90 ℃～105 ℃)， 物料干燥温度越高、 铺设厚度越小， 完全干燥所需时间越短， 干燥效率越高．

2) Weibull分布函数能够很好地模拟厨余垃圾的干燥过程， 对厨余垃圾干燥过程的预测、 调控和工艺优化具有重要意义： 干燥温度越高、 铺设厚度越小， α越小， 表明完全干燥所需时间越短， 干燥效率越高；β受物料铺设厚度、 干燥温度等因素影响较小， 反映出干燥前期存在短暂升速干燥阶段， 而整体呈现降速干燥特征．

3) 估算水分扩散系数Dcal在1.078×10-7～2.651×10-7m2/s之间， 随干燥温度升高、 物料厚度减小而增大； 1.4，2.8，4.2 cm厚厨余垃圾的干燥活化能分别为19.24，18.68，22.45 kJ/mol， 表明适中厚度的厨余垃圾干燥更为容易； 2.8 cm左右的物料铺设厚度较适合干燥， 较优干燥温度可根据进一步测试耗能情况后进行选择．