过渡态理论速率系数与标准态和热力学函数*
郭思宇,孙 如,徐敏敏,李淑瑾
(苏州大学材料与化学化工学部,江苏 苏州 215123)
在20 世纪前叶,简单碰撞理论和过渡态理论这两个反应速率理论是化学动力学发展史上的重要里程碑。在统计力学和量子力学的基础上建立的反应速率理论,英国化学家波兰尼(Michanel Poanyi)称之为过渡态理论,而美国化学家艾林(Henry Eyring)将其称为活化络合物理论。过渡态或活化络合物是反应系统势能面上的马鞍点,可借助于量子力学理论计算出。只要知道过渡态的结构,可以根据光谱数据用统计力学的方法,不需要通过化学动力学实验就能计算出反应速率系数的理论值, 所以又称为绝对反应速率理论[1-2]。
化学动力学过渡态理论中有一基本假设 “由反应物分子变成生成物分子,中间要经过一个过渡态, 而形成这个过渡态需要一定的活化能,过渡态与反应物之间建立化学平衡”[1]。用热力学方法推导过渡态速率系数时,涉及过渡态与反应物之间化学平衡的热力学平衡常数,而热力学平衡常数与热力学标准状态有关。各种物理化学教材在化学热力学部分都有较详细热力学标准态的叙述。用热力学方法推导过渡态理论的化学反应速率系数时选择标准浓度c(1 mol/dm3)为热力学标准态得到准平衡常数[1,3]。在化学动力学中,常用反应物质的浓度(mol/dm3)随时间的变化率来表示化学反应的速率,而在气相化学反应中,压力比浓度容易测定,所以经常用反应物质的压力(Pa或者kPa)随时间的变化率来表示化学反应的速率,同一化学反应,由于化学反应速率的表示不同,则会带来反应速率系数的不同。
随着量子化学计算在化学反应动力学中的应用,过渡态理论使化学动力学研究进入一个崭新的阶段。用量子化学方法可计算反应系统的势能面,得到摩尔活化热力学函数值是以标准压力p(105pa)为标准状态的,用过渡态理论计算速率系数,如取标准浓度c(1 mol/dm3)为标准态,则两种标准状态下的摩尔活化热力学函数则不尽相同,需要换算。本文选以理想气体反应为例用热力学方法推导了两种标准态下(标准浓度c和标准压力p)过渡态理论反应速率系数及摩尔活化热力学函数(如摩尔活化吉布斯自由能、摩尔活化化熵等)相互之间的关系,并用量子化学计算研究案例讨论了两种标准态下结果之间的转换。这些结果对常见物理化学教材过渡态理论部分忽略之处给予了补充,有利于物理化学过渡态理论的教学和加深其应用的理解。
1 两种热力学标准态下的过渡态理论速率系数
过渡态理论认为化学反应中反应物通过形成过渡态(TS≠)而成为生成物,过渡态与反应物之间很快达成并保持热力学平衡,这为认识化学反应奠定了理论基础。过渡态也称活化络合物,它是反应系统势能面反应坐标上的马鞍点。过渡态的寿命是极短的,目前研究过渡态物种的实验手段有吸收与发射光谱、激光光电子能谱和实时飞秒检测等。量子化学计算可获得过渡态的谐振动频率、几何构型和反应的热力学函数值等。用统计热力学方法可以根据过渡态理论的基本假设推导出两种热力学标准态下反应的速率系数。
1.1 标准浓度c(1 mol/dm3)为热力学标准态的过渡态理论速率系数
在物理化学教材中,用标准浓度c(1 mol/dm3)为热力学标准态的速率系数与活化热力学函数的关系式为式(1)或式(2)[1]:
(1)
(2)
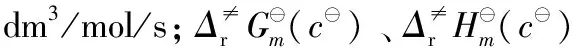
1.2 标准压力p(105 Pa)为热力学标准状态的过渡态理论速率系数
用热力学方法推导过渡态理论速率常数,根据过渡态理论的基本假设之一,活化络合物和反应物之间存在快平衡,该反应的准热力学平衡常数与反应物质热力学标准态的化学势有关。
1.2.1 两种热力学标准状态下标准化学势之间的关系
设理想气体混合物中任意一组分B,其浓度为cB(mol/dm3),压力为pBPa。
在温度T时,选标准浓度c(1 mol/dm3)为热力学标准态,则该组分B的化学势μB表示为式(3):
(3)
若选标准压力p(105pa)为热力学标准态,则该组分B的化学势μB表示为式(4):
(4)
对于理想气体,用SI制单位,则pB与cB的关系为式(5):
pB=cBRT×103
(5)
将式(5)代入式(4)整理后得式(6):
(6)
化学势μB是状态函数,与热力学标准态的选择无关,比较式(3)和式(6)可得式(7):
(7)
式(7)为在温度T时标准浓度c(1 mol/dm3)为热力学标准态的化学势和标准压力p(105pa)为热力学标准态之间的关系。物理化学教材[1]中也给出了两种标准态化学势之间的关系式,但忽略了物理量之间单位的换算,式(7)则考虑了物理量之间单位的换算。
1.2.2 两种热力学标准状态下标准摩尔活化Gibbs自由能之间的关系
根据热力学标准吉布斯自由能变化值与标准化学势之间的关系,在过渡态理论中,化学反应体系过渡态与反应物之间在两种热力学标准状态下标准活化Gibbs自由能分别可表示为式(8)和式(9):
(8)
(9)
对于单分子气相化学反应ABC → AB+C 或者双分子气相化学反应A+BC → AB+C,根据过渡态理论基本假定,它们的机理分别为(i)或(ii):
(i)
或
(ii)
在反应机理(i)中,∑vB=0;而在反应机理(ii)中∑vB=-1。用n代表反应物的分子数,则机理(i)和机理(ii)的∑vB=1-n。
整理式(7)、(8)和(9)三式,得式(10):
(10)
1.2.3 标准压力p(105Pa)为热力学标准状态的过渡态理论速率系数
式(1)为大家熟知的标准浓度c(1 mol/dm3)为热力学标准态的速率系数,将式(10)代入式(1),则有:
(11)
在化学反应动力学中,用压力表示的速率系数kp[(Pa)1-n/s1]与浓度表示的速率系数k[(mol·dm-3)1-n/s]之间的关系为:
kp=k(RT×103)1-n
(12)
将式(12)代入式(11),则有:
(13)
式(13)是选择标准压力p为热力学标准态时过渡态理论速率系数的计算公式,与文献[4]的结论一致。
2 两种热力学标准态下标准摩尔活化焓、标准摩尔活化熵之间的关系
2.1 两种热力学标准态下标准摩尔活化焓
在式(10)两边除T后 对T偏微分,则有:
(14)
根据吉布斯-亥姆霍兹(Gibbs-Helmholtz)方程,则得到两种热力学标准态下标准摩尔活化焓的关系式(15):
(15)
2.2 两种热力学标准态下标准摩尔活化熵
在式(10)两边对T偏微分,则有式(16):
(16)
由热力学基本方程式可得式(17):
(17)
3 过渡态理论速率系数研究案例
以我们课题组研究反式白藜芦醇(ROH)修复2′-脱氧鸟苷自由基[10]中的部分结果为案例,说明过渡态理论在研究反应体系动力学方面的应用。在研究修复反应系统时运用量子化学密度泛函理论(DFT) 计算获得了修复反应系统中反应物、过渡态的优化构型、各反应机理的吉布斯自由能垒,在此基础上运用过渡态理论计算了各反应的速率系数,揭示主要反应机理,确定了主要修复位点。用过渡态理论计算得到的修复反应速率常数与实验上多酚化合物修复脱氧鸟苷自由基的速率常数(108~109dm3/mol/s)一致。
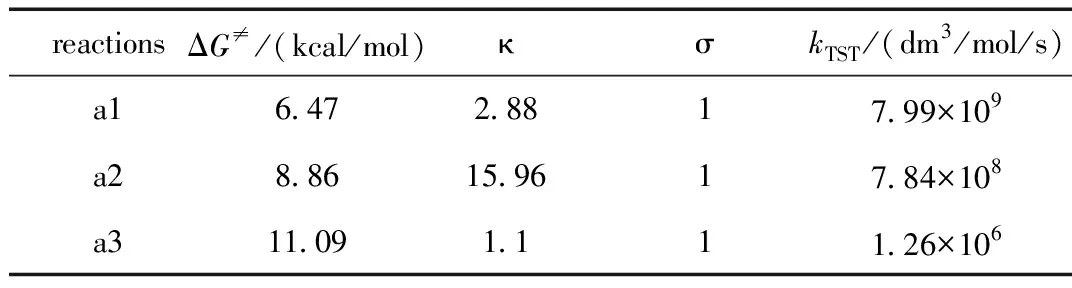
表1 反应吉布斯自由能垒ΔG≠, 隧道校正因子κ,反应路径简并度σ和在1 mol/dm3标准状态下的速率系数kTSTTable 1 Gibbs Free Energy Barriers ΔG≠,the tunneling correction κ, the reaction path degeneracy σ and the rate constants kTST at 1 mol/dm3 standard state
在用过渡态理论计算速率系数时,涉及到了两种热力学标准状态下反应吉布斯自由能垒ΔG≠之间的换算关系式(10)。在298.15 K时,以苯为非极性溶剂模型中ROH通过氢转移(HT)机理修复2′-脱氧鸟苷碱基脱氢自由基的主要修复反应在文献[10]中标记为a1、a2和a3。表1归纳了文献[10]中a1~a3反应吉布斯自由能垒(ΔG≠)、隧道效应校正因子(κ)、反应路径简并度(σ)和在1 mol/dm3标准状态下过渡态理论的速率系数kTST。
在实际应用过渡态理论计算反应的速率系数时,考虑了反应的隧道效应校正因子(κ)和反应路径简并度(σ), 则式(1)修正为式(18):
(18)
在式(18)中,吉布斯自由能垒ΔG≠的热力学标准态为标准浓度c(1 mol/dm3),而用量子化学计算得到的表1中反应吉布斯自由能垒ΔG≠的热力学标准态为标准压力p,因此不能用表1中的ΔG≠代入式(18)计算速率系数。
标准浓度c和标准压力p的两热力学标准态的反应吉布斯自由能垒斯需根据式(10)进行换算。以表1中反应a1为例, 两者之间的换算为:ΔG≠(c)=ΔG≠(p) -1.90=4.57 kcal/mol,将ΔG≠(c)代入式(18),则可计算得到kTST=7.99×109dm3/mol/s。依次类推根据式(18)可以计算出反应a2和a3的kTST。
过渡态速率理论在化学动力学研究中有很广泛的应用,理解两种热力学标准状态下过渡态理论的速率系数及标准摩尔活化热力学函数之间的关系显得尤为重要。
4 结 语
通过上述讨论可知,标准摩尔活化吉布斯自由能、标准摩尔活化焓和标准摩尔活化熵是与热力学标准态有关的物理量,基于过渡态理论的基本假定,我们较为详细地用热力学方法导出了两种热力学标准态下过渡态理论速率系数公式、标准摩尔活化吉布斯自由能、标准摩尔活化焓和标准摩尔活化熵之间的关系。本文是对物理化学教材中热力学方法处理过渡态理论内容的补充,有助于对过渡态理论的理解和应用。

