基于循环谱和深度神经网络的调制识别算法

葛 战，伍 警，李 兵，蒋鸿宇，周 劼

(中国工程物理研究院 电子工程研究所，四川 绵阳 621900)

0 引言

通信信号经过周期变换(如采样、调制及编码等)处理后，会呈现周期平稳特性[1]。不同调制信号会在循环谱上表现出不同的特性，可以此进行调制样式分类[2]。传统基于循环谱的调制识别方法包含循环谱图生成、人工选取特征以及分类器设计等步骤[3]。实际中，由于通信信号循环谱数据量较大，一般需要采取降维方法对数据进行降维。然而，不同的降维方法以及特征的选取和门限的划分均会影响分类器的分类性能[4]。

与传统识别方法不同，近年来，深度学习(Deep Learning,DL)技术由于其在图像识别等领域中表现出的优异性能被引入至调制识别研究当中[5-7]。该技术直接以数据作为输入，能够学习到更加丰富的特征信息,自动完成特征提取及信号分类,显著提高了识别率[8-10]。文献[11-13]采用卷积神经网络(Convolutional Neural Network,CNN)以及自编码器(Auto-Encoder,AE)等深度网络通过对信号的循环谱进行学习实现调制识别。然而,以上工作未考虑信号循环谱数据量较大这一问题，直接导致训练时间过长。

针对该问题，本文首先分析了采用CNN直接对未降维的谱数据学习分类，以及采用主成分分析(Principal Component Analysis,PCA)和AE方法对谱数据降维，再采用CNN实现调制分类的3种方法。然后，在此基础上提出了基于AE和CNN相互联合的网络结构——AE-CNN，同时完成数据降维和调制识别工作。网络以循环谱的循环频率轴投影(α-profile)作为AE的输入输出，实现对输入数据的压缩，同时将AE的隐层输出，即压缩后的数据，送入至CNN实现学习分类。2个网络通过联合训练最终实现调制识别。实验结果表明，该网络结构无需人工选取特征，直接以信号的循环谱作为输入，与基于PCA和AE降维的方法相比，能够充分地利用输入数据的特征信息，获得较高的识别性能；与基于CNN的方法相比，能够大幅地减少训练时间，并在识别性能上有一定的提升。

1 问题分析

1.1 循环谱分析

通信信号在经过周期变换后会表现出二阶周期特性，是一种广义循环平稳信号[1]。其自相关函数Rx(t;τ)=Rx(t+τ/2,t-τ/2)本质上是对信号的瞬时谱在频率轴上下移动一定的值后做相关，通过相关可以得到不同循环频率上的谱累计，进而产生冗余谱峰。由于不同样式的通信信号会产生不同类型的谱峰，因此可以用此区分通信信号类型。

Rx(t;τ)可展开成傅里叶级数的形式[14]：

(1)

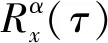
对于循环平稳信号可使用统计平均代替时间平均，得到：

(2)

信号的循环谱可表示为循环自相关函数的傅里叶变换，即：

(3)

实际中，计算循环谱的算法一般是通过对循环周期图做平滑处理后得到，主要包括离散频率平滑算法和离散时间平滑算法[1]。由于高精度谱相关计算复杂度较高，因此常采用快速计算方法[1]。基于离散时间平滑的快速算法主要有：FFT累积算法(FFT Accumulation Method，FAM)和比特谱相关算法等[1]。本文采用FAM算法计算调制信号的循环谱，然后对循环谱α轴进行投影，提取到用于信号调制识别的数据样本：

(4)

α轴投影包含了信号的特征信息，相比较循环谱图本身能够有效地降低数据量，常用于频带调制信号识别。6种调制信号在信噪比为6 dB时的循环谱图及α轴投影如图1所示。

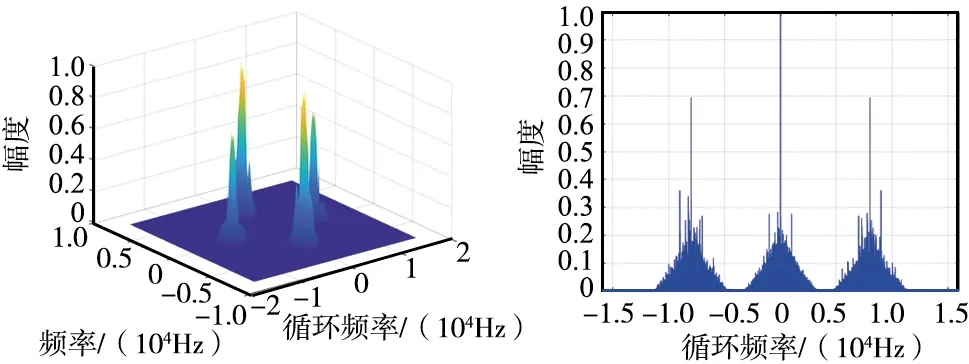
(a) BPSK

由图1可以看出，各调制信号在不同的循环频率上会呈现出不同的谱峰，因此可以根据谱峰数量实现对其分类。传统方法通过设定门限找出α轴投影上的谱峰数量，然后通过比较谱峰数量实现调制识别。本文采用深度神经网络直接提取循环谱α轴上的特征信息，无需再设定门限寻找谱峰。该方法能够更充分地挖掘有益于分类的特征信息，实现识别率的提升。

1.2 数据降维

由于采用FAM算法计算出的循环谱数据量较大且含有冗余信息，如果直接采用神经网络训练会造成训练时间过长。因此，在送入神经网络训练之前一般需要进行降维，使数据能够更容易使用，并一定程度地去除噪声，同时降低计算开销。常见的降维方法有PCA、局部线性嵌入(Locally Linear Embedding，LLE)、线性判别分析(Linear Discriminant Analysis,LDA)、T-SNE以及AE等[15]。由于PCA计算复杂度较低而被广泛使用，但是该方法需要选取合适的主成分数才能取得最佳性能。本文采用AE实现对循环谱数据的降维操作，相比较PCA方法，AE是一种非线性变换方法，能够学习更深层次的特征信息。经实验，其他方法，如LLE，LDA和T-SNE，在对本文的循环谱数据进行降维时耗时非常大，暂不考虑。

2 算法设计

2.1 CNN

对于规模较大的数据，全连接网络由于参数众多，会造成训练时间过长，而CNN则能够有效降低训练复杂度，并且采用多卷积核能够提取到更为丰富的特征信息，因此本文采用CNN实现对输入数据的学习与分类。

CNN本质上是一种具有更深层次的前馈神经网络，通过采用局部连接和权值共享使网络学习参数大幅降低，能够在大规模数据上进行学习训练。通常由卷积层、池化层和全连接层组成[16-17]。

卷积层采用卷积核提取输入数据的隐含特征，即特征图。卷积操作过程如下：

(5)

池化层主要是用于对卷积后的数据执行下采样操作，用于数据的降维：

(6)

全连接层则用于分类，常用Softmax分类器。训练过程会将分类器的输出与样本对应的标签信息进行比较，采用反向传播法迭代更新网络参数使损失函数最小，损失函数由交叉熵确定：

(7)

式中，m，j，k分别为样本数量、样本标签以及调制种类；q(·)为指示函数；lnp(·)为样本zi的概率。

考虑CNN在未降维循环谱数据上的分类性能(方法1)。所采用的CNN结构如图2所示，由输入模块、特征提取模块和分类模块组成，其中输入根据不同的方法，分别为循环谱数据、PCA降维后的数据或AE的隐层输出。特征提取模块由3个卷积层和3个池化层串联组成，卷积层采用一维CNN，相比二维CNN，一维CNN参数更少，训练速度更快,能够有效减少训练时间。卷积块1～3中，卷积核大小均为1×3，通道数依次为64，32和24，激活函数采用ReLU。池化层采用1×2的平均池化，进一步缩减网络参数。文中所提出的方法均采用该CNN结构。

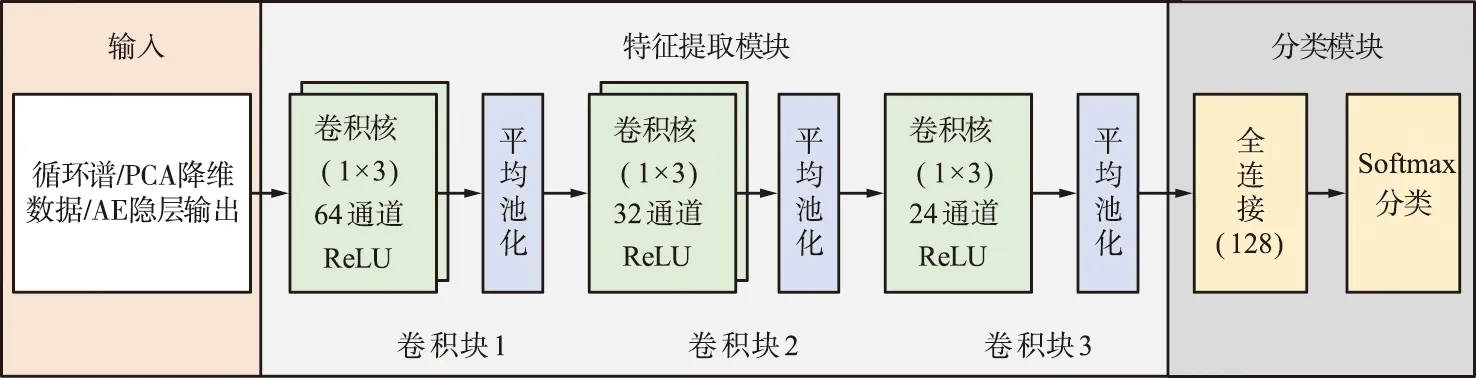
图2 CNN方法结构Fig.2 Structure diagram of CNN method

2.2 PCA

针对循环谱降维问题，首先采用PCA方法实现。PCA常用于高维数据的降维，是一种线性变换，通过将原始数据投影到若干维度得到不相关的线性表示，进而提取数据的主要特征分量[18-19]。这些主成分保留了数据的主要信息，能够表征原始数据。常用的PCA算法包括基于特征值分解和奇异值分解(Singular Value Decomposition,SVD)2种方法。

本文采用基于SVD的PCA方法对训练集进行降维，然后把降维后的数据送入CNN实现分类(方法2)，基于PCA方法的识别框图如图3所示。降维后的数据规模大幅减小，神经网络训练时间也能够大幅降低。同时，本节通过选取不同的主成分数量，验证了其对调制识别性能的影响。

图3 PCA方法结构Fig.3 Structure diagram of PCA method

2.3 AE

AE是一种无监督深度学习方法，能够实现对循环谱数据的降维。与PCA不同，既能对输入数据进行线性变换也能进行非线性变换。其主要目的是通过模型的学习使得输出能够重构出输入，主要由编码器和解码器组成[6,12]，其网络结构如图4所示。

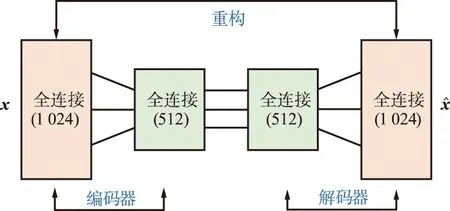
图4 AE网络结构Fig.4 Structure diagram of AE network

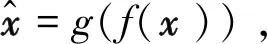
(8)

本文采用全连接网络实现AE，其中编码器和解码器成对称结构，分别由2层全连接网络构成，具体参数如图4所示。实验中AE的输入和输出为各信号的循环谱。经过学习，AE能够实现对输入数据的降维，其隐层能够提取到输入数据的特征信息，然后将这些特征信息送入到CNN即可实现分类(方法3)。

2.4 AE-CNN

方法3首先采用AE对输入数据降维，然后采用CNN进行分类，类似于2.2节基于PCA的方法，这2个学习过程彼此独立。需要注意的是，该方法会把数据降维时的误差引入至后续的分类学习当中，造成分类性能下降。本节在方法1和3的基础上，提出了将AE数据降维和CNN信号分类进行相互联合学习的网络结构(方法4)，如图5所示。

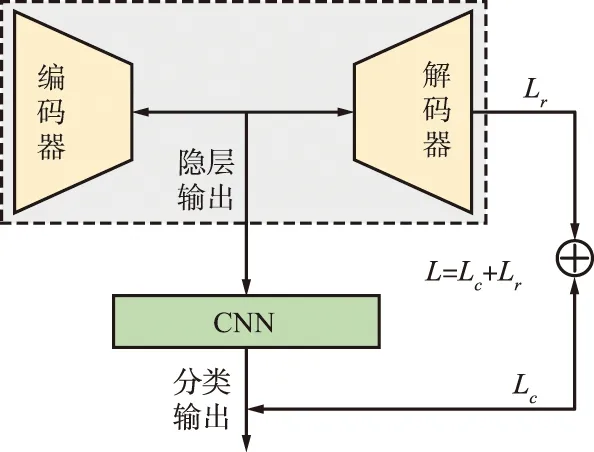
图5 AE-CNN网络结构Fig.5 Structure diagram of AE-CNN network

该网络结构采用AE对数据降维，同时将其隐层输出至CNN，然后将2个网络的损失函数相加，通过反向传播算法更新误差使得2个网络能够联合训练。网络中AE有助于对输入数据的重构精度分类，同时CNN的分类准确性又有助于重构误差的减小，因此通过联合训练有助于提升分类准确率。该网络的损失函数如下：

L=Lc+Lr。

(9)

2.5 识别方法步骤

本文采用AE和CNN相互联合的方法，对循环谱进行降维的同时实现调制识别。具体步骤可概括为：

① 生成6种通信调制信号，该信号为具有载波频率的频带信号；

② 采用FAM算法计算各调制信号的循环谱；

③ 获取各调制信号循环谱α轴的投影，产生训练集、验证集以及测试集；

④ 方法1实现：采用CNN直接对循环谱训练集进行训练，实现分类；

⑤ 方法2实现：采用PCA对训练集降维，然后送入CNN实现学习分类；

⑥ 方法3实现：采用AE进行降维，然后采用CNN对AE的隐层输出学习分类，2个步骤独立；

⑦ 方法4实现：采用AE进行降维的同时将其隐层输出至CNN，将2个网络的损失函数相加，进行联合训练分类；

⑧ 训练完成后，在测试集上分别验证不同方法的性能，完成信号的调制分类。

3 算法仿真及分析

3.1 数据集构建及训练设置

产生训练所需的训练样本、验证样本和测试样本。本次仿真共产生6种经过标注的信号(BPSK，QPSK，2FSK，4FSK，MSK和OQPSK)。载波频率为4 kHz，符号率为1 kHz，采样率为16 kHz，符号长度为1 000，成型滤波器为升余弦滤波器，过渡带宽为0.35。数据首先由Matlab 2017a产生，然后采用FAM算法计算出每种信号的循环谱图。每种信号的信噪比为-6～10 dB，每隔1 dB产生1 000个数据，其中900个用于训练，100个用于验证。测试集则按照上述参数单独生成，每信噪比下样本数量为200。样本标签采用one-hot编码格式。

实验中网络结构由TensorFlow深度学习框架搭建，采用ADAM作为优化器。初始学习率、批处理大小以及训练次数分别设置为lr=0.001，batchsize=100及epoch=50。训练中采取变更学习率策略，当网络模型在验证集上的损失变化连续5个epoch小于0.001时，学习率缩减10倍，有助于训练精度的提升。

3.2 CNN方法性能分析

方法1：将6种调制信号的循环谱训练数据直接送入CNN。在测试集上6种调制信号的平均识别率如图6所示。由图6可以看出，随着信噪比的增加信号识别率也在增加。通过计算，信噪比在-6～10 dB不同样式的总体平均识别率为86.5%。

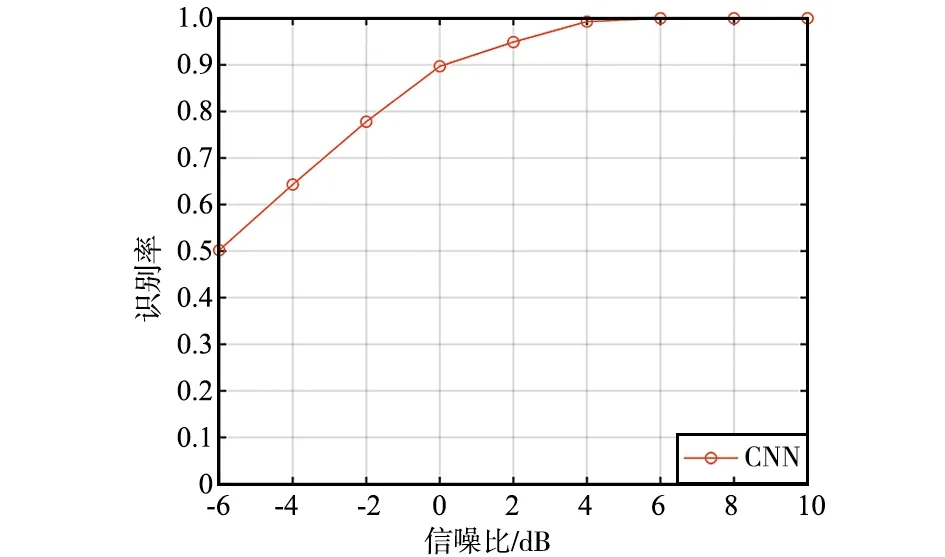
图6 不同信噪比下6种信号的平均识别率Fig.6 Average correct recognition probability of six signals under different SNR

每种信号的识别率如图7所示。由图7可以看出，2FSK，4FSK和MSK的性能较优，BPSK和QPSK的次之，OQPSK的性能最差。识别结果与图1所表现的一致，图1中2FSK，4FSK和MSK所包含的特征信息相比较更多，更容易区分；而OQPSK与QPSK较为相似，增加了区分难度。

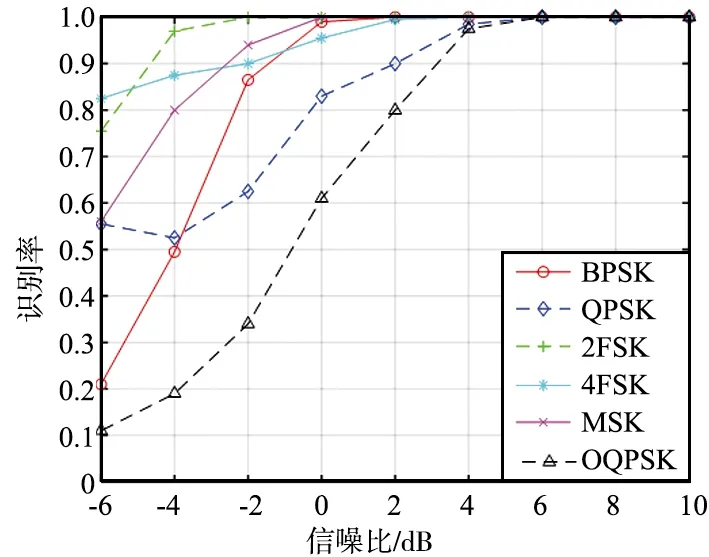
图7 不同信噪比下各信号的识别率Fig.7 Correct recognition probability of each signal under different SNR

3.3 PCA方法性能分析

方法2：首先采用PCA对训练数据进行降维，然后使用CNN分类，以达到减少训练时间的目的。实验中PCA主成分数分别选取16，24，48，192及512。不同主成分数的分类性能如图8所示。图8中不同主成分数(16～512)对应的总体平均识别率为85.9%，86.1%，85.8%，84.6%和83.0%。由此看出，随着主成分数的增加，分类性能呈下降趋势。

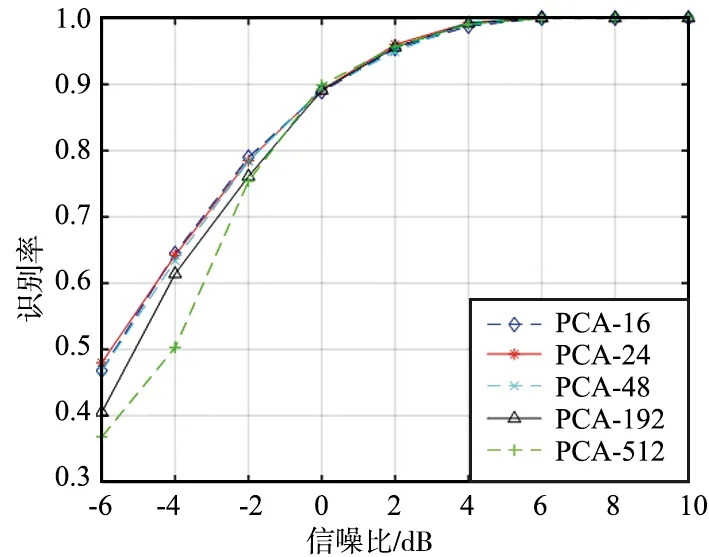
图8 PCA方法不同主成分的识别率Fig.8 Correct recognition probability of PCA method with different principal components

主成分数为24和192时，模型在训练集和验证集上的训练过程如图9所示。由图9可以看出，随着主成分数的增加，训练集上的识别率在增加，但验证集上的识别率却在减小。主要是由于当主成分数增加时，在训练集上能够提取到更多的特征信息，然而当该PCA参数应用到测试集时提取的特征信息与训练集会存在更多的差异，造成测试集性能下降。因此在实际中采用PCA降维时，主成分数会影响识别性能，需要多次实验寻找最优数值。经验证，在主成分数为24时性能较优，接近方法1中的分类性能。由此可见，该方法在经过数据降维后仍能得到较优的性能，表明原始数据中含有较多的冗余信息，合适的数据降维对分类性能影响较小。

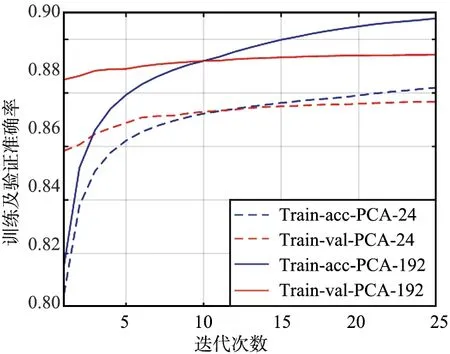
图9 不同主成分训练性能对比Fig.9 Training performance comparison with different principal components

3.4 AE&CNN独立训练性能分析

方法3：采取AE和CNN独立训练的方式。同PCA方法，首先采用AE对训练集降维，其编码器的输入和解码器的输出采用相同的数据。AE训练完成后把训练集送入该网络，其隐层即可提取出降维后的特征信息。然后，将这些特征信息送入至CNN网络即可实现分类，2个网络单独训练。

AE中4个全连接网络选取4组不同的参数，分别为“1 024-512-512-1 024”“512-256-256-512”“96-48-48-96”“48-24-24-48”。不同参数下该方法的识别结果如图10所示，对应的总体平均识别率分别为85.6%，85.1%，84.8%，83.4%。可以看出，AE模型中随着参数数量的减少，识别性能会有所下降。主要是由于当全连接神经元减少时，AE提取的信息不足所造成。因此，在实际中需要选择合适的网络参数才能达到理想的识别性能。

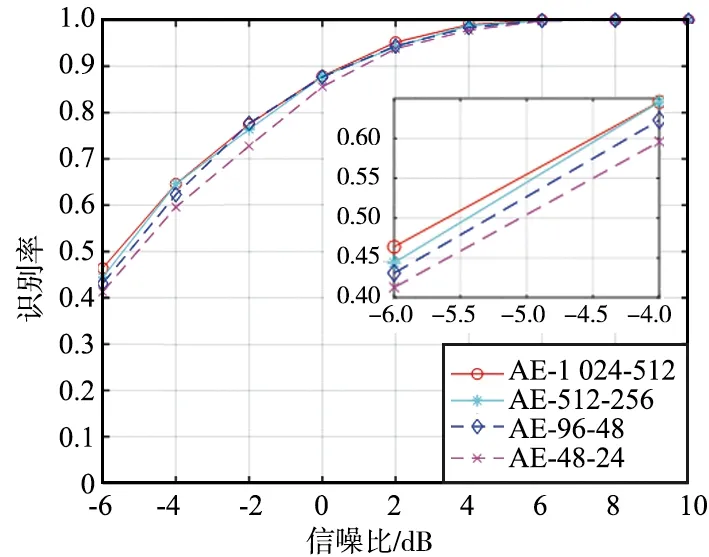
图10 不同网络参数时AE&CNN的识别率Fig.10 Correct recognition probability of AE&CNN with different network parameters

方法3在全连接参数为“1 024-512-512-1 024”时，-6～10 dB信噪比范围内6种不同信号的总体识别率为85.6%，与方法1和方法2相比分别下降0.9%和0.5%。该方法面临的问题同方法2，即在采用AE降维时会引入误差信息，送入随后的分类网络时，造成识别性能的下降。

3.5 AE-CNN联合训练性能分析

方法4：提出的AE-CNN模型通过将负责数据降维的AE和负责调制分类的CNN两个深度网络联合训练实现信号的调制识别。同方法3，网络中AE的参数设定为“1 024-512-512-1 024”，方法1～4在不同信噪比下的平均识别率如图11所示。由图11可以看出，基于AE-CNN联合的方法相比其他3种方法性能有明显的提高。通过计算，AE-CNN方法在-6～10 dB的总体识别率为87.7%，与方法1～3相比分别提升了1.2%，1.6%和2.1%。

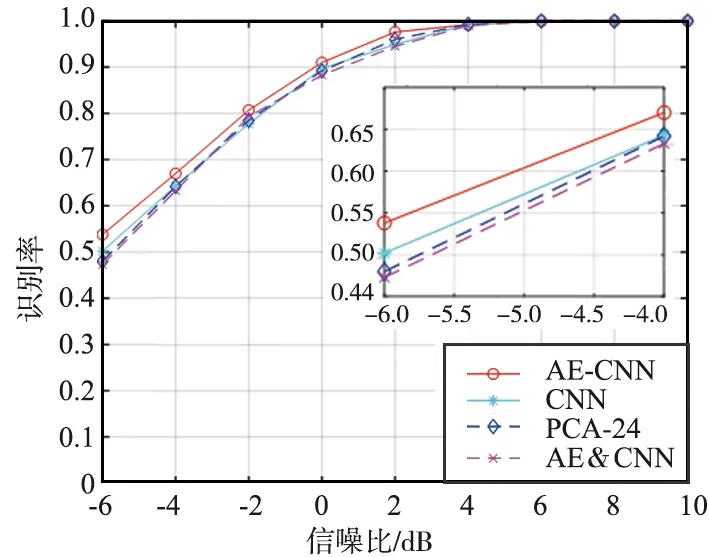
图11 方法1～4识别性能对比Fig.11 Recognition performance comparison of method 1～4

每种信号在不同信噪比下的识别率如表1所示。与图7相比较，该方法在低信噪比时对BPSK的识别性能较优，而对MSK的识别性能有所下降，对于OQPSK的识别性能则优于方法1，其余几种样式的识别性能较为相似。

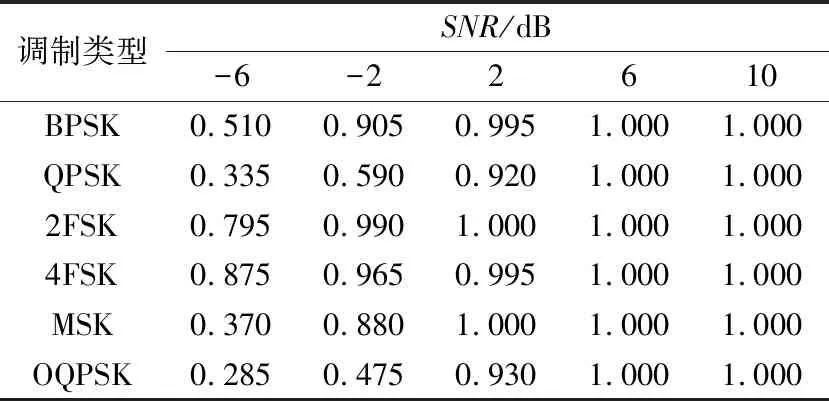
表1 不同信噪比下各信号的识别率Tab.1 Correct recognition probability of each signal under different SNR

测试AE-CNN中4个全连接网络选取不同参数时的性能。AE的参数设置同3.4节，不同参数下AE-CNN网络的识别性能如表2所示。由表2可以看出，与AE&CNN方法不同，AE-CNN选取不同的参数时对识别性能影响不大。由于联合训练时2个网络起到相互促进作用，有助于减少误差累积。

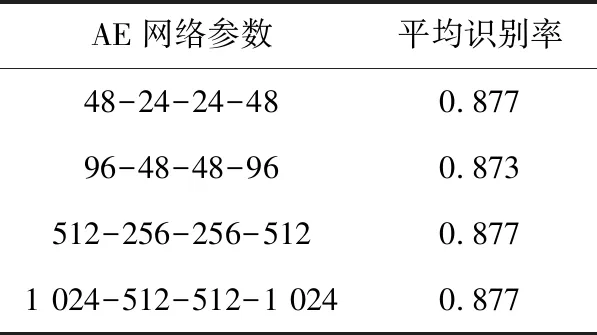
表2 不同网络参数时AE-CNN的识别率Tab.2 Correct recognition probability of AE-CNN method with different network parameters

3.6 训练时间分析

本文采用软硬件平台的主要参数为Intel CPU主频2.4 GHz，显卡为NVIDIA GTX3090，深度学习框架为TensorFlow2.4。采用方法1～4在相同的训练集上进行训练，统计训练过程中每epoch所消耗的时间如图12所示。

由图12可以看出，采用CNN单独训练时，所消耗时间较多，约66.5 s。采用PCA降维时所消耗时间最少。在选取3种不同主成分(文中设定为24，192和512)时每epoch训练耗时几乎一致，约11 s。AE&CNN方法在3组不同的参数(如表2前3组参数)下迭代时间约为22 s。AE-CNN方法在相同的参数下迭代时间约为18 s。可以发现，方法2～4在3组不同的参数下每epoch训练时间几乎一致。其中AE-CNN方法在提高了识别率的同时相对于CNN方法的训练时间也大幅地减少。

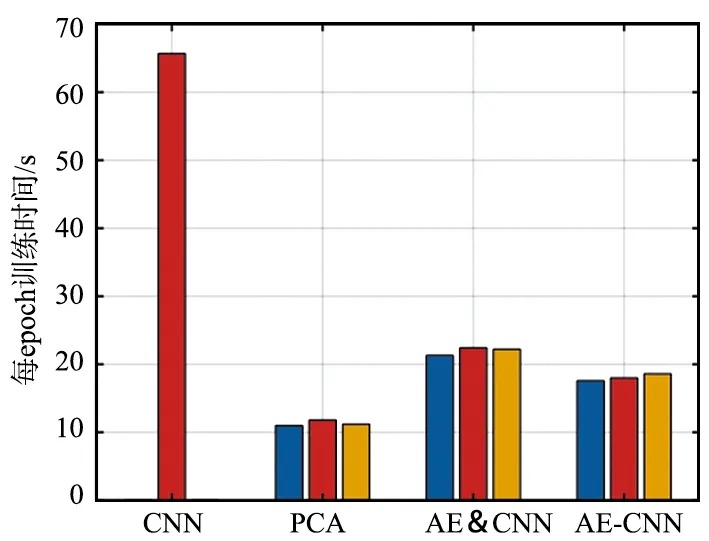
图12 方法1～4每epoch训练耗时Fig.12 Training time per epoch of method 1～4

4 结束语

本文采用深度神经网络针对通信信号的循环谱开展调制识别问题研究。在分析了基于CNN，PCA以及AE三种方法的基础上，提出了一种基于AE和CNN相互联合的网络结构同时完成数据降维和调制识别的算法。该方法在对循环谱数据压缩的同时采用CNN实现调制分类。2种网络在训练过程中相互促进，其中AE的重构精度能够促进分类性能的提升，而CNN的分类精度又有助于减小重构误差。实验结果表明，该方法能够获得更优的识别性能，并且在训练时间上相对于单独采用CNN也大幅减少。后续工作会考虑采用卷积AE和稀疏AE等方法进一步提升识别性能。