基于混合扰动的差分隐私贝叶斯神经网络
张攀峰,杨智威,张文勇,敬 超*
(1.桂林理工大学 信息科学与工程学院,广西 桂林 541006;2.广西嵌入式技术与智能系统重点实验室,广西 桂林 541006)
0 引言
基于人工智能的大数据技术已逐步成为大数据分析的主流技术,相关应用也逐步渗入到国防、教育、科学、生产和生活等方方面面。但基于深度学习理论的人工智能技术,因其泛化能力不足,导致训练数据面临信息泄露的风险。差分隐私技术是保护数据隐私的有效途径,通过对深度学习加入差分隐私技术,能够为模型提供一种无需加密的隐私保护能力,这种隐私保护方式使模型在被攻击时无法完全还原训练数据,从而防止隐私数据的泄露。
差分隐私的提出,首先应用到数据发布上。这种基于输入扰动 (Input Perturbation,ITPN)[1-5]的差分隐私,能够在一定程度上保护数据隐私,但使用这种数据去训练深度学习模型,得到的训练模型可用性不高。而保留原始数据仅扰动模型拟合数据的方法被逐渐提出。
输出扰动(Output Perturbation,OTPN)[6]是一种直接把噪声加到模型最优值上的方式。这种方式最大的问题是,噪声分布是固定的,攻击者可以反复对模型输入,去推断模型的真实输出结果。而在反向传播过程中的扰动方式,无法通过反复输入,推断出训练集。
目标扰动 (Objective Perturbation,OEPN)[6]是通过对算法的目标函数添加噪声,去干扰模型对数据的拟合。目标扰动本质上是一种随机正则化。梯度扰动(Gradient Perturbation,GTPN)[7-8]是直接把噪声加到梯度上,使模型在求解最优梯度时产生偏移。这2种扰动方式都是在模型的反向传播过程中干扰模型对数据的拟合。但以上这些扰动方法对模型进行隐私保护时,都不可避免地造成模型的可用性降低。
Moments Accountant[7,9-10]的提出,量化了反向传播的隐私保护效果。但Moments Accountant在选择高斯分布计算雷尼散度上,只选择了高斯噪声分布和混合高斯分布,且混合高斯分布与训练集无关。而差分隐私的定义中,对比的是相邻数据集的分布,不是噪声分布与数据集无关的混合高斯分布。这会使隐私评估出现不够精确的问题。
针对以上问题,提出了一种综合应用输出扰动和目标扰动的差分隐私贝叶斯神经网络——基于混合扰动的差分隐私贝叶斯神经网络(Differential Privacy Bayesian Neural Networks Based on Mixed Perturbation,DPBNNMP),且主要做了如下几点工作:
① 对于差分隐私加入神经网络导致模型可用性下降的问题,采取分割网络权重方法,确保模型的学习能力;
② 使神经网络在前向传播过程和反向传播过程都满足差分隐私;
③ 对于①中产生的前向传播隐私开销进行推导。
1 相关知识
1.1 贝叶斯神经网络
贝叶斯神经网络(Bayesian Neural Networks,BNNs)[11-13]与传统神经网络的主要区别在于目标函数。
对于一个参数为w,数据集为D的BNNs,其w的最大后验概率(Maximum a Posteriori,MAP)为:
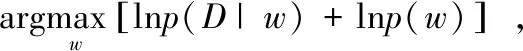
(1)
式中,wMAP为BNNs权重w的MAP;D为训练数据;p(w|D)为权重w在数据集D上的后验概率分布。
为了获得权重w的MAP估计,采用变分学习的方式找到一个概率q(w|θw)近似权重w的后验概率。为此利用KL散度来最小化概率q(w|θw)和p(w|D)的距离,有:
(2)
式中,p(D|w)为给定神经网络权重w关于数据集D的似然函数;p(w)是w的先验概率。BNNs的损失函数为:
F(D,θw)=KL[q(w|θw)=p(w)]-Eq(w|θw)[lnp(D|w)]。
(3)
在最小化目标函数之前,必须对后验概率抽样权重的标准差σ进行参数化,即σw=ln(1+eρw),ρw是标准差σw的参数。目标函数F(D,θw)的参数θw=(μw,ρw),μw是对应分布的数学期望值。而神经网络的权重w=μw+ln(1+eρw)·ζ,ζ~N(0,I),I为示限函数。模型参数θw决定了神经网络的权重w。使用随机梯度下降算法来求解最优参数θw=(μw,ρw),从而优化神经网络的权重w。
由无偏蒙特卡罗抽样可以把F(D,θw)转化成如下形式:
(4)
BNNs提供了一种崭新求解最优化网络权重的方式,认识不确定性的引入也为当前网络泛化能力提供了一个置信度,为神经网络提供另一种角度来思考参数优化问题。
BNNs的目标函数本身带有正则化项,即q(wi|θw),该项的作用相当于正则化。
1.2 差分隐私
Dwork等[5]于2006年提出的一种严格数学定义的隐私保护算法,即差分隐私[7,11-12,14],主要应用于相邻数据集隐私保护。
Triastcyn等[10]推导了贝叶斯方式下的隐私核算计算过程,着重在相邻数据集各自分布在雷尼散度上的值。
定义1ε-差分隐私[4-7]。对任意的相邻数据集d和d′,d,d′∈D,任意算法M:D→R和输出结果S⊆R,若不等式
Pr[M(d)∈S]≤eεPr[M(d′)∈S],
(5)
成立,则满足ε-差分隐私。式中Pr[M(d)∈S]指算法M在d数据集上输出属于实数集R子集S的概率,ε≥0。
定义2强贝叶斯差分隐私[10,15-17]。对任意的相邻数据集d和d′,d,d′∈D,任意算法M:D→R和输出结果S⊆R,算法参数w1=M(·),若不等式
Pr[LM(w,d,d′)≥ε]≤δ,
(6)
成立,则满足(ε,δ)-差分隐私[4-7]。式中,Pr[·]是概率,LM(w1,d,d′)定义如下:
(7)
一般称LM(w,d,d′)为隐私损失,p(w|d)是神经网络权重w在数据集d上的条件概率,0≤δ≤1,ε≥0。
定义3(ε,δ)-差分隐私[4-7]。对任意的相邻数据集d和d′,d,d′∈D,任意算法M:D→R和输出结果S⊆R,若不等式
Pr[M(d)∈S]≤eεPr[M(d′)∈S]+δ,
(8)
成立,则满足(ε,δ)-差分隐私。式(8)中Pr[M(d)∈S]指算法M在d数据集上输出属于实数集R子集S的概率,0≤δ≤1,ε≥0。
(ε,δ)-差分隐私[4-7]的提出,放宽了对以往ε-差分隐私的定义。通过添加σ,对隐私保护的条件放宽,(ε,δ)-差分隐私[4-7]指以一定概率δ使ε-差分隐私失效。
敏感度用来衡量2个相邻数据集各自训练的算法的差别,差别越大,隐私保护能力也就越好。
定义4敏感度[7]。对于函数f:D→R,d和d′是2个相邻数据集,d,d′∈D,则|f(d)-f(d′)|的最大值为该函数的敏感度S(·),定义为:
S(f)=max|f(d)-f(d′)|。
(9)
差分隐私机制,通常使用噪声干扰的方式来完成,高斯机制是主要方式之一。高斯机制是通过添加高斯噪声的方式,来扰动算法对数据的拟合,以此达到隐私保护效果的机制。
定义5高斯机制[1]。对于函数f:D→R,任意算法M:D→R,数据集d,d′∈D,高斯机制定义为:
M(d)=f(d)+N(μ,σ2),
(10)
式中,N(μ,σ2)为噪声的高斯分布。
高斯机制目前主要有4种应用:ITPN[6],OTPN[6],OEPN[6]和GTPN[6]。
定义6目标扰动。设Q(wn|θw)=lnq(w|θw),w′=w+N(μ,σ2),w为人工神经网络权重,有如下定义:
Q(w′|θw)=lnq(w+N(μ,σ2)|θw),
(11)
式中,N(μ,σ2)为噪声的高斯分布;θw为算法参数;q(w+N(μ,σ2)|θw)为权重w被扰动后的概率分布。
OEPN通常选择目标函数进行扰动,使神经网络在反向传播中出现干扰。
为了衡量算法加入差分隐私的隐私保护效果,Abadi等[7]提出Moments Accountant去追踪隐私开销。而隐私核算主要通过雷尼散度来衡量相邻数据集各自分布的差别,以追踪应用高斯机制前后的数据集分布的差异。
定义7雷尼散度[9,14]。对于2个定义在实数集R上的P概率分布和Q概率分布,λ>1,雷尼散度被定义为:
(12)
式中,Ex~Q(·)为分布Q上的数学期望;λ为雷尼散度的秩。
2 混合扰动的差分隐私贝叶斯神经网络
2.1 输出扰动
DPBNNMP是在BNNs[11,13,18-19]的基础上增加了训练数据隐私保护的部分。它的改进一方面体现在网络结构上,如图1所示,对神经元线性变换做了如下改变:
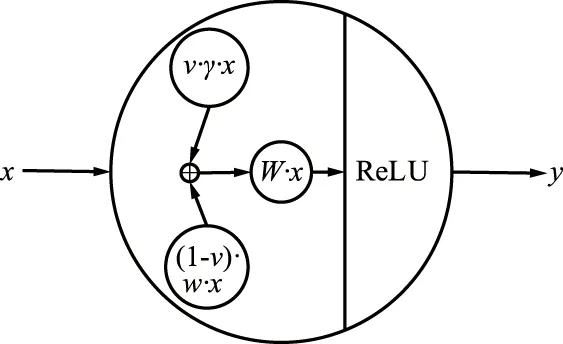
图1 基于混合扰动的神经元Fig.1 Neuron based on mixed perturbation
h(x)=x·W,
(13)
式中,W为DPBNNMP的权重,且W=(1-v)·w+v·γ,w是网络权重,γ是噪声权重,v为噪声贡献度,0≤v≤1;x为模型输入值;“·”表示相乘操作。
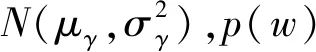
p[(1-v)·w+v·γ]≤eεp(w)。
(14)
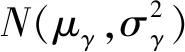
(15)
式中,W=(1-v)·w+v·γ。对式(15)左右取对数,有:
(16)
当v=0时,有0≤ε。
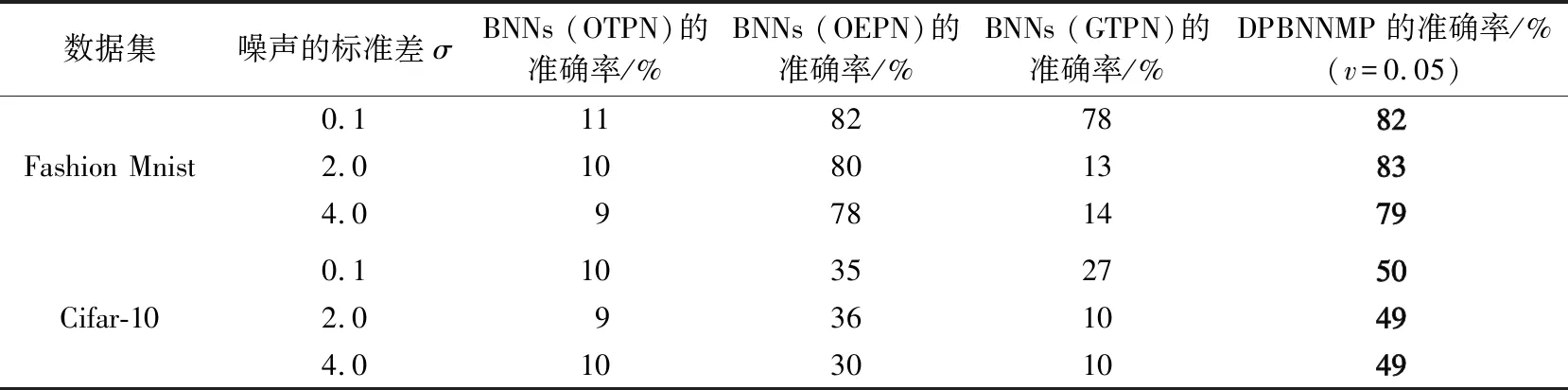
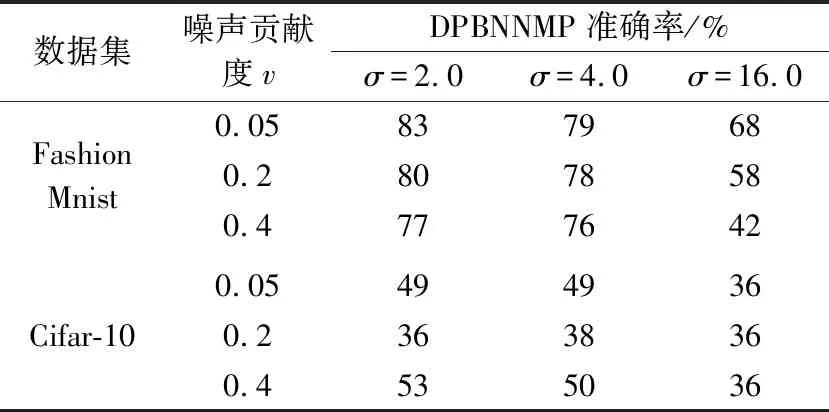
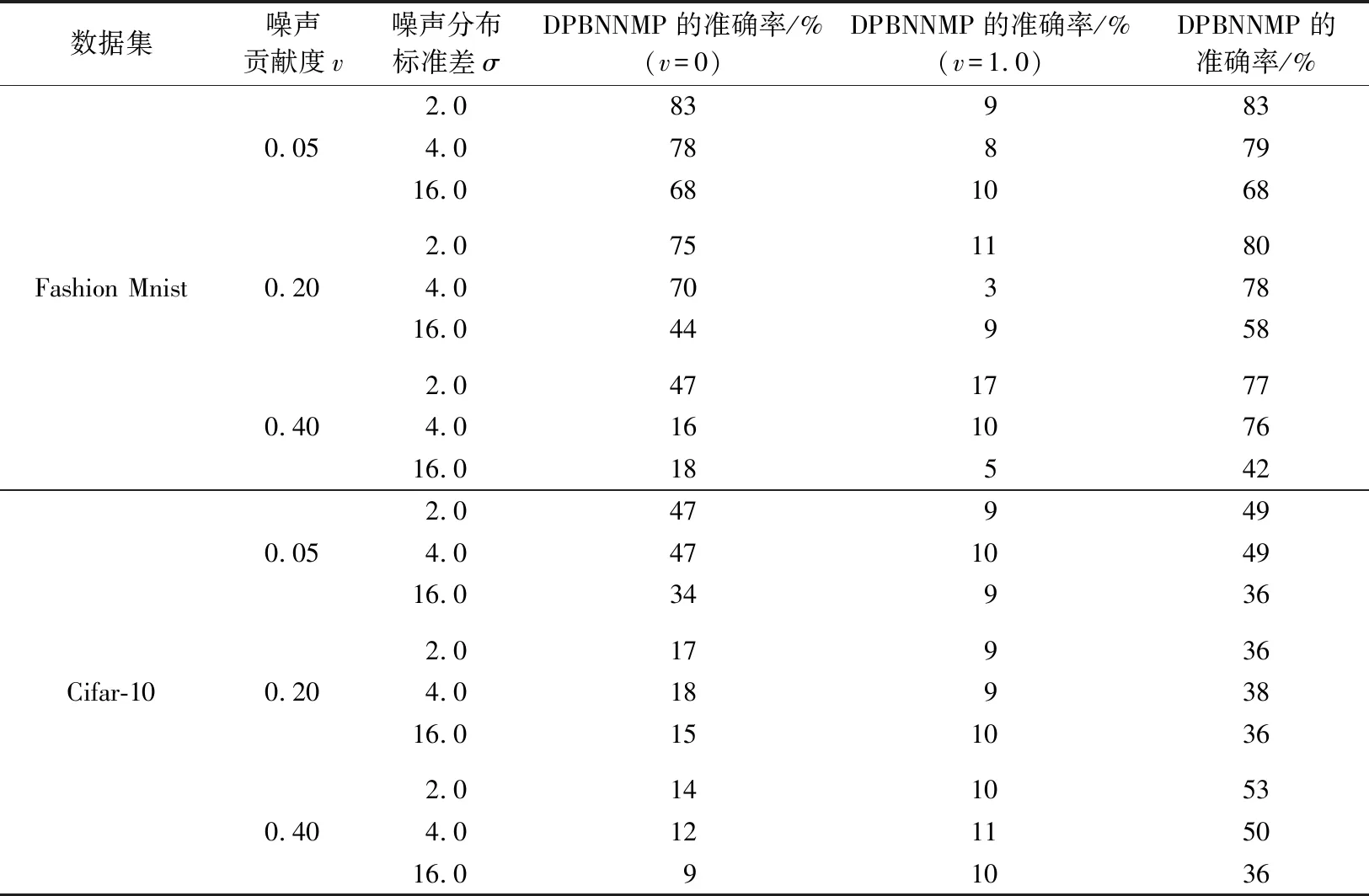
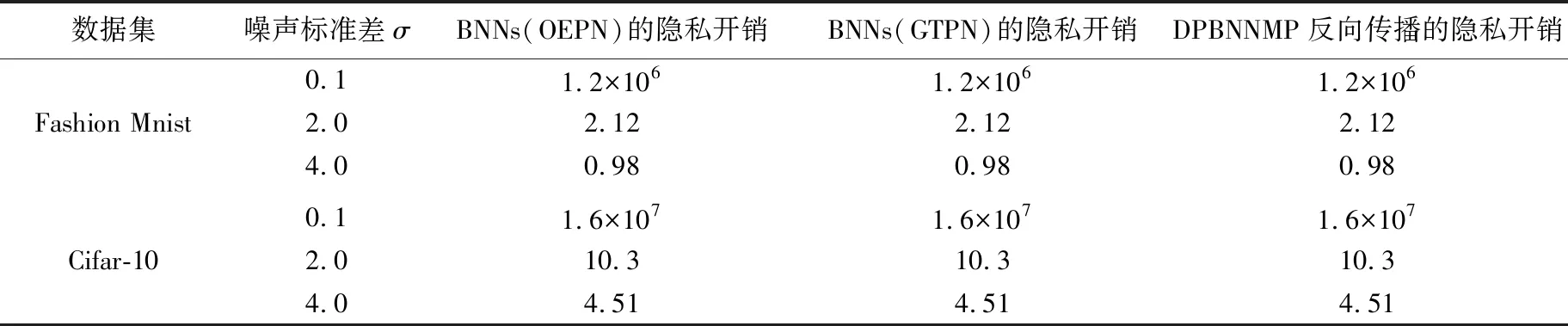
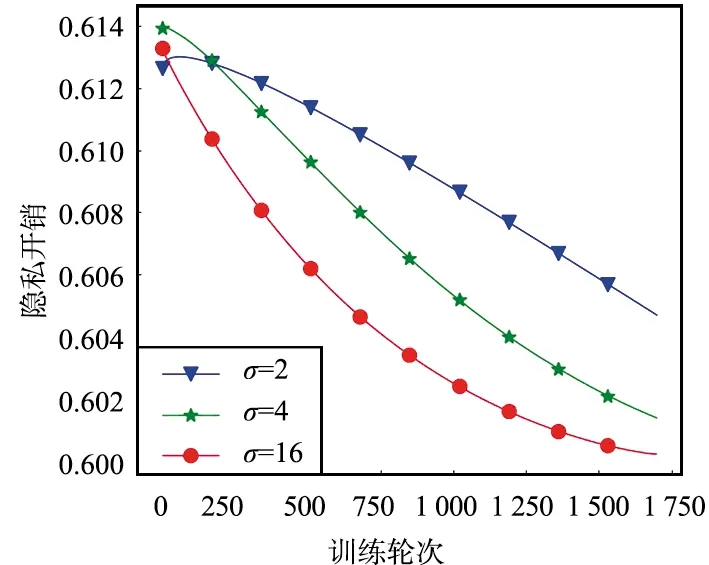
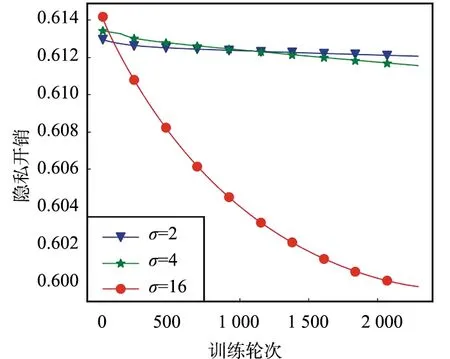
当0 (17) 当v=1时,有: (18) 当OTPN满足如上条件时,网络权重满足ε-差分隐私。 OTPN示意如图2所示。A代表v·γ·x,B代表(1-v)·w·x,C代表W·x。主体结构仍然和普通神经网络一样,不同点是把传统的神经网络的权重分割成网络权重w和噪声权重γ,相应的偏差也分为神经元偏差和噪声偏差。其中,v决定噪声权重对W的贡献度,(1-v)决定网络权重对W的贡献度,一般v<0.5。ReLU是ReLU激活函数,y是神经元的输出。 图2 DPBNNMPFig.2 Diagram of OTPN 当m个神经元都满足ε-差分隐私,根据文献[9],由这m个神经元组成的神经网络满足如下关系: (19) 且该神经网络满足(ε′,δ)-差分隐私。 为了保证噪声权重完成扰动的任务,就需要采取2.2节的方式混合扰动神经网络。 由于除了网络权重,DPBNNMP内部还有噪声权重,在没有任何扰动时,噪声权重并不能完成扰动的任务,所以本文将OEPN作用到神经网络的目标函数上,再利用优化算法,把噪声传递给噪声权重,使DPBNNMP在反向传播过程中满足差分隐私保护。 通过贝叶斯公式对噪声权重建模,得到以下概率模型。 一个被随机高斯噪声干扰后的噪声权重γ,通过前向传播,添加到DPBNNMP的网络权重w上,获得一个干扰后DPBNNMP的权重W,算法输入的数据集为D。γ的后验分布,由贝叶斯公式有: (20) 式中,p(γ|D,w)为γ的后验概率;p(γ)为γ的先验概率;p(D|γ,w)为关于噪声权重γ和网络权重w的似然函数;p(D|w)为给定网络权重w后D出现的概率。 用MAP得到γMAP: (21) 式中,γMAP为DPBNNMP噪声权重γ的最大后验概率;D为训练数据;p(γ|D,w)为噪声权重γ在数据集D和网络权重w上的后验概率分布。 为了得到p(γ|D,w)的近似,引入一个概率q(γ|θγ)去近似p(γ|D,w),所以有: Eq(γ|θγ)[lnp(D|γ,w)], (22) 式中,p(D|γ,w)为给定DPBNNMP的网络权重w和噪声权重γ关于数据集D的似然函数;p(γ)为γ的先验概率。 因此,得到噪声后验概率形式的目标函数为: G(D,θγ)=KL[q(γ|θγ)=p(γ)]- Eq(γ|θγ)[lnp(D|γ,w)], (23) 式中,KL[q=p]是KL散度,度量q概率到p概率的距离。在最小化G(D,θγ)之前,需要将θγ参数化为θγ=(μγ,ργ),ργ是重参数化后标准差的参数[11],μγ是对应θγ的数学期望值。 由无偏蒙特卡罗抽样把噪声后验分布的目标函数转化成如下形式: (24) 式中,q(γi|θγ)概率相当于普通神经网络目标函数中的正则化部分。在求解最优值时,用来惩罚第i个噪声权重γ。 根据定义6,式(24)要满足差分隐私,可以向式(24)中q(γi|θγ)部分引入任意高斯噪声,使其满足差分隐私保护,所以有: lnp(γi)-lnp(D|γi,wi), (25) 式中,N(μ,σ2)为任意高斯分布。根据定义1,任意高斯噪声N(μ,σ2)必须满足如下关系,才能使噪声权重满足差分隐私: p(γ+n)≤eεp(γ), (26) (27) 当输入的任意噪声满足式(27)时,神经元的噪声权重满足ε-差分隐私。根据式(19),整个神经网络的噪声权重满足(ε′,δ)-差分隐私。 为了更新DPBNNMP的参数,由式(4)和式(25)可以得到DPBNNMP的目标函数: lnp(γi)+lnq(wi|θw)- lnp(wi)-2lnp(D|γi,wi), (28) 式中,N(μ,σ2)为任意噪声的分布;θγ和θw为算法F(D,θw,θγ)待学习的参数;w为网络权重;γ为噪声权重;D为数据集;q(γi+N(μ,σ2)|θγ)为第i个噪声权重OEPN的后验概率估计;q(wi|θw)为第i个网络权重的后验概率估计;p(γi)为第i个噪声权重的先验概率;p(wi)为第i个网络权重的先验概率;p(D|γi,wi)是参数为γi和wi关于数据集D的似然函数。 2.4.1 算法思想 DPBNNMP算法的隐私保护方式是在目标函数上引入一个高斯噪声分布抽样,干扰噪声权重对数据的拟合,即OEPN,又在前向传播过程中把噪声权重加到网络权重上,即OTPN,具体算法如下。这样就使得前向传播和反向传播都满足差分隐私。 算法1 DPBNNMP算法输入 数据{(x1,y1),(x2,y2),(x3,y3),…,(xN,yN)},学习率η,批次大小B,噪声贡献度v,OEPN的数学期望μ和标准差σ。输出 训练好的DPBNNMP模型 ① θw=(μw,ρw),θγ=(μγ,ργ)∥用高斯分布N(0,0.12)[18]初始化网络权重和噪声权重的μw和μγ,用高斯分布N(-3.0,0.12)[18]初始化网络权重和噪声权重的ρw和ργ。② for t in range(T):∥进行T次训练。③ 抽样|Bt|个数据,Bt∈{(x1,y1),(x2,y2),…,(xN,yN)}。④ ζ~N(0,I) ∥以高斯分布N(0,I)抽样出ζ,这里I=1.0。⑤ w=μw+ln(1+eρw)·ζ∥计算当前网络权重的值。⑥ γ=μγ+ ln(1+eργ)·ζ∥计算当前噪声权重的值。⑦ W=(1-v)∙w+v∙γ∥进行OTPN,得到DPBNNMP的权重。⑧ 以W为神经网络的权重,同时W和|Bt|个数据进行前向传播。⑨ f(Bt,θw,θγ)=lnq(γt+N(μ,σ2)|θγ)-lnp(γt)+lnq(wt|θw)-lnp(wt)-2lnp(xBt,yBt|γt,wt)∥进行OEPN。⑩ ∇μγ←∂f(Bt,θw,θγ)∂γ+∂f(Bt,θw,θγ)∂μ∥计算噪声权重的μ参数梯度。 ∇ργ←∂f(Bt,θw,θγ)∂γ 1+exp(-ρ)+∂f(Bt,θw,θγ)∂ρ∥计算噪声权重的ρ参数梯度。 ∇μw←∂f(Bt,θw,θγ)∂w+∂f(Bt,θw,θγ)∂μ∥计算网络权重的μ参数梯度。 ∇ρw←∂f(Bt,θw,θγ)∂w 1+exp(-ρ)+∂f(Bt,θw,θγ)∂ρ∥计算网络权重的ρ参数梯度。 μγ←μγ-η∇μγ,ργ←ργ-η∇ργ∥更新模型参数。 μw←μw-η∇μw,ρw←ρw-η∇ρw∥更新模型参数。end for 2.4.2 算法描述 首先,对DPBNNMP进行建模,分别定义模型参数θw=(μw,ρw)和θγ=(μγ,ργ),再输入数据集D,学习率η和噪声贡献度v,OEPN的数学期望μ和标准差σ。然后,每次抽取|Bt|份数据去训练模型。最后,开始训练模型参数。 (1) 步骤③~④都是抽样操作,步骤③是抽取训练样本,步骤④为参数化后的标准差提供随机性。 (2) 步骤⑤~⑥把标准差σ参数化为ln(1+eρ)。后验分布的参数为θw=(μw,ρw)和θγ=(μγ,ργ)。使用重参数化技巧[11]有γ=μγ+ ln(1+eργ)·ζ,w=μw+ln(1+eρw)·ζ,“·”操作是相乘。重参数化是为了能够用梯度下降更新后验分布。步骤⑦是OTPN,使DPBNNMP的网络权重满足差分隐私,通过上一步得到的噪声权重γ与噪声贡献度v的乘积,与缩放(1-v)倍的网络权重w相加,得到扰动后的神经元结点权重。 噪声贡献度v使算法具备退化成没有隐私保护的BNNs的能力。由于网络权重在反向传播过程中并没有受到扰动,所以网络权重会尽可能地拟合数据集,得到一个与训练集呈高相关性的权重分布。在训练完毕后,使v=0,DPBNNMP就会失去隐私保护能力。而没有扰动的网络权重也奠定了前向传播隐私开销计算的基础。相比之下,深度学习差分隐私[7]训练的网络只能得到扰动后的权重分布。 2.4.3 前向传播的隐私核算(隐私保护效果评估) 本小节对隐私保护效果进行详细分析和公式推导。隐私保护效果可以通过隐私核算(Privacy Accounting)[7]来评价。 在(ε,δ)-差分隐私[5-7]中,δ一定时,ε越小说明隐私保护越好。 隐私核算能够追踪到ε的上确界,这个上确界称为隐私开销。隐私核算主要通过雷尼散度来衡量相邻数据集各自分布的差别,以追踪应用高斯机制前后的数据集分布的差异。 由于DPBNNMP分割了神经元的权重,区别于传统方式[6-8,10]。所以对于神经网络前向传播的隐私开销计算需要重新考虑。 神经网络当前隐藏层的每个神经元相互独立,当前隐藏层的隐私开销由当前隐藏层的每个神经元隐私开销的线性组合而成。假设当前隐藏层是一个整体,当前隐藏层的输出结果作为下一层隐藏层的输入,根据组合理论[9],这2层的隐私开销为当前隐藏层和下一层隐藏层的隐私开销的线性相加。 加入差分隐私保护后,计算神经网络相邻数据集分布的雷尼散度是一件困难的事。因为高斯噪声干扰模型后,这个模型对应的数据集分布是无法观测的,而知道的分布只有干扰前训练集的分布。在只知道一个数据集分布的情况下无法计算相邻数据集的雷尼散度。但是,神经网络在相邻数据集上,各自训练后得到的神经网络权重分布与各自训练神经网络的数据集正相关,也就是说,相邻数据集上的雷尼散度[9]与相邻数据集分别训练神经网络后,得到各自神经网络权重分布之间的雷尼散度,呈正相关。所以,直接计算神经网络权重之间的雷尼散度来评价隐私保护的效果反而是一件较为简单的事。这也是把神经网络权重分割为噪声权重和网络权重的原因之一。计算雷尼散度之前,必须先计算隐私损失。所以,对于相邻数据集各自第t次训练DPBNNMP对应的权重值Wt,根据马尔可夫链,Wt只与Wt-1和数据集有关,所以隐私损失L可以写成如下形式: (29) 式中,W=(1-v)·w+v·γ;d和d′是2个相邻数据集;λ是雷尼散度[9]的阶。 隐私损失是计算隐私核算过程的重要一步。根据定义2和定义7[7,9-10],对于迭代T次的算法,雷尼散度数学期望部分呈如下形式: 设迭代算法迭代T次,W1,W2,…,WT为对应迭代次数1,2,…,T的DPBNNMP权重,L为迭代算法的隐私损失,λ为雷尼散度[9]的阶,d和d′是2个相邻数据集,有: (30) 式中,EW(·)为求解数学期望。 证明:对于迭代算法有: 由赫尔德不等式有: 证毕。 通过上述计算,只是得到雷尼散度中的数学期望部分,还需要再进一步计算雷尼散度。 根据常用的一元连续分布函数的雷尼散度[9,14],有如下引理: 引理1[9,14]设N1为高斯分布N(μ1,σ12),N2为高斯分布N(μ2,σ22),T为迭代算法M的迭代次数,则雷尼散度为: (31) 通过引理1,可以计算到2个分布的雷尼散度。但ε无法直接计算得到,所以需要求得ε的取值范围,才能计算出隐私开销。根据式(30)和式(31)得到如下形式的重尾约束。 定理1 重尾约束(Tail Bound)[7,10],设DPBNNMP随迭代次数T变化的参数为W1,W2,…,WT,2个相邻数据集d和d′的后验分布p(Wt|Wt-1,d)和p(Wt|Wt-1,d′),对于一个常数δ,隐私开销有如下约束: (32) (33) (34) 式中,E1是在W服从N2高斯分布上求解数学期望;E2是在参数W服从N1高斯分布上求解数学期望。 在DPBNNMP前向传播过程中,网络权重的分布与噪声权重的分布是独立分布。所以式(30)和式(31)中的N1(N2)取噪声贡献度v=0(v<5.0)时,神经网络权重分布等于网络权重分布与噪声权重分布相加的分布,即W~N((1-v)·μw+v·μγ,(1-v)2·ln2(1+eρw)+v2·ln2(1+eργ))。 仿真实验是在2块Intel(R) Xeon(R) Gold 6234 CPU 3.3 GHz,128 GB内存,2块NVIDIA GeForce RTX3090上完成。 BNNs采用了表1中LetNet-5结构的卷积神经网络[13,18]结构,该结构由2层卷积层、2层池化层、2层全连接层,外加1层分类层softmax组成。 表1 LetNet-5模型结构Tab.1 LetNet-5 model structure 在实验评估过程中使用2份数据集:一份是Fashion Mnist;另一份是Cifar-10。Fashion Mnist是一份意在替代Mnist数据集的灰度图像数据集。数据集详情如表2所示,Fashion Mnist单张图像大小为28 pixel×28 pixel,通道数为1,一共有70 000张图片,60 000张是训练集,10 000张是测试集。Fashion Mnist包括T恤、套衫、裤子、裙子、凉鞋、外套、汗衫、运动鞋、靴和包等10种标签。Cifar-10数据集包含60 000张图片,每张图都有3个通道,每个通道的大小为32 pixel×32 pixel。训练集为50 000张图片,测试集为10 000张图片,一共有10种标签,分别为飞机、小汽车、鸟、猫、鹿、狗、蛙、马、船和货车。 表2 数据集详情Tab.2 Dataset details 部分超参数如表3所示,BNNs的学习率η=10-3,批次大小为250,雷尼散度δ=10-5,噪声高斯分布的数学期望为0,神经网络在Fashion Mnist数据集上训练150轮次,在Cifar-10上训练2 500轮次。 表3 部分超参数Tab.3 Part of hyperparameters 不同扰动方式的准备率如表4所示。Fashion Mnist数据集下,σ=0.1时,DPBNNMP(v=0.05)的准确率与OEPN的BNNs的准确率相等,DPBNNMP(v=0.05)的准确率比GTPN的BNNs准确率高出4%。σ=2.0时,DPBNNMP(v=0.05)准确率比OEPN的BNNs的准确率高出3%,比GTPN的BNNs的准确率高出70%。σ=4.0时,DPBNNMP(v=0.2)的准确率比OEPN的BNNs的准确率高出1%,比GTPN的BNNs准确率高出65%。 在Cifar-10数据集下,σ=0.1时,DPBNNMP(v=0.05)准确率比OEPN的BNNs的准确率高出15%,比GTPN的BNNs准确率高出23%。σ=2.0时,DPBNNMP(v=0.05)准确率比OEPN的BNNs的准确率高出13%,比GTPN的BNNs的准确率高出39%。σ=4.0时,DPBNNMP(v=0.05)的准确率比OEPN的BNNs的准确率高出19%,比GTPN的BNNs准确率高出39%。 不同扰动方式在不同的高斯噪声分布下对BNNs的可用性影响不同。表4中,OTPN通过对神经网络的最优权重值加入扰动,导致收敛困难。OEPN通过对BNNs的正则化部分加入高斯噪声,进行随机扰动,能够有效地收敛。GTPN在梯度下降优化过程中,对梯度直接加入高斯噪声,导致优化困难,所以难以收敛。DPBNNMP(v=0.05)在表4情况下都有较好的收敛。 表4 不同扰动方式的准确率Tab.4 Accuracy of different perturbations DPBNNMP在不同的高斯噪声分布和不同的噪声贡献度可以得到不同的可用性。噪声贡献度v与目标扰动σ对DPBNNMP的影响如表5所示,在噪声贡献度一定时,随着噪声高斯分布的标准差越大,模型的准确率就越低。不同的噪声贡献度对模型整体的准确率影响有限。 表5 噪声贡献度v与目标扰动σ对DPBNNMP的影响Tab.5 Influence of different values of v and σ on accuracy of DPBNNMP 网络权重的可用性和噪声权重的可用性如表6所示,训练完毕的DPBNNMP,在预测阶段,使噪声贡献度等于0时,模型可用性由网络权重完全贡献;使噪声贡献度等于1.0时,模型可用性由噪声权重完全贡献。越低的噪声贡献度,网络权重完全贡献的准确率与DPBNNMP权重的准确率就越接近,这是由于网络权重对神经网络权重的贡献更高。越高的噪声贡献度,导致噪声权重在整个DPBNNMP权重中占比过大,需要更大的高斯噪声才能保证噪声权重不去拟合数据,而更大的高斯噪声很难让DPBNNMP权重去拟合数据。表6中也显示出,在相同的噪声贡献度下,更大的高斯噪声标准差,DPBNNMP的准确率也就越低,网络权重的可用性也由于更大的高斯噪声标准差变得更低。噪声权重贡献的准确率并不高,表明噪声权重没有拟合数据集,完成了OTPN的任务。 表6 网络权重的可用性和噪声权重的可用性Tab.6 Availability of noise weights and networks weights Moment Accountant的提出是用来计算在反向传播扰动的隐私开销的,所以反向传播的隐私核算使用Moment Accountant对比OEPN,GTPN和混合扰动的隐私开销。而Moment Accountant主要是通过噪声高斯分布的雷尼散度来评估隐私开销。反向传播的隐私开销如表7所示。在相同σ下,OEPN,GTPN和混合扰动(σ=0.05)都是相同的隐私开销。在Fashion Mnist数据集实验中,σ=0.1时,3种方式都产生1.2×106的隐私开销;σ=2.0时,3种方式都产生2.12的隐私开销;σ=4.0时,3种方式都产生0.98的隐私开销;在Cifar-10数据集实验中,σ=0.1时,3种方式都产生1.6×107的隐私开销;σ=2.0时,3种方式都产生10.3的隐私开销;σ=4.0时,3种方式都产生4.51的隐私开销。由表4和表7可以看出,在相同的反向传播隐私开销下,DPBNNMP得到更高的准确率。 表7 反向传播的隐私开销Tab.7 Privacy overhead of back propagation 前向传播的隐私开销通过神经网络权重分布与神经网络的网络权重分布的雷尼散度计算而来。 Fashion Mnist数据集上的前向传播隐私开销如图3所示。在Fashion Mnist数据集下,v=0.2时,随着噪声的标准差的增加,隐私开销不断地下降,且高噪声标准差比低噪声标准差得到更低的隐私开销;v=0.4时,隐私开销随着噪声的标准差的增加,隐私开销也在下降,且高噪声标准差比低噪声标准差得到更低的隐私开销。 (a) v=0.2 Cifar-10数据集下的前向传播隐私开销如图4所示。在Cifar-10数据集下,v=0.2时,随着噪声的标准差的增加,隐私开销不断地下降,且高噪声标准差比低噪声标准差得到更低的隐私开销;v=0.4时,隐私开销随着噪声的标准差的增加,隐私开销也在下降,且高噪声标准差比低噪声标准差得到更低的隐私开销。 在相同的噪声贡献度下,隐私开销会随着高斯噪声标准差的增加而更快地下降,表明更高的高斯噪声标准差,能够得到更好的隐私保护效果。而噪声贡献度决定着整个隐私开销的大小,这是由于在计算雷尼散度时,更大的噪声贡献度,得到更小的网络权重贡献度,更小的网络权重贡献度导致网络权重更差的数据拟合能力,而神经网络权重整体的可用性不会因为噪声贡献度的大小变差,也就导致网络权重的分布和神经网络权重分布之间的雷尼散度更大。隐私开销和雷尼散度成正比,所以隐私开销更大。 (a) v=0.2 数据隐私保护关系国家安全,其研究一直是信息安全领域的重要内容。DPBNNMP主要对深度学习中训练数据集提供隐私保护。它采用分割神经网络权重的方式,把神经网络权重分为网络权重和噪声权重分布。这种方式将输出扰动结合到优化过程中,且目标扰动只干扰噪声权重的目标函数,不会干扰网络权重的目标函数,所以在训练过程中,优化算法能够朝着更好的方向前进,使得DPBNNMP在相同的反向传播隐私开销上,比加入单一目标扰动和梯度扰动的BNNs得到更好的模型准确率和泛化能力。网络权重与噪声权重的和是扰动后的数据集对应的神经网络权重分布,网络权重本身是训练集对应的神经网络权重分布。通过这2个分布能够计算一个与相邻数据集高度相关的隐私开销;并且这个与相邻数据集相关的前向传播隐私开销会随着噪声方差的增大而下降,并在更大的噪声标准差上得到更好的隐私保护效果。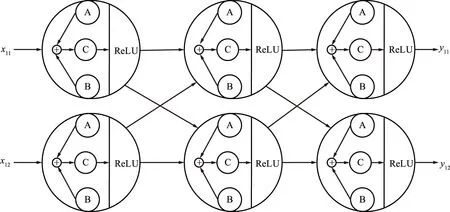
2.2 目标扰动
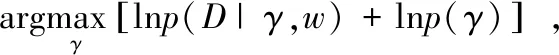
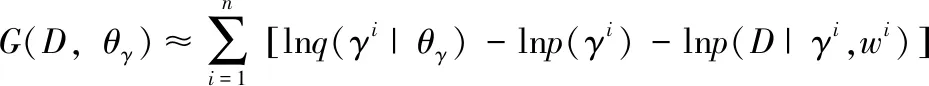
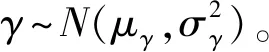
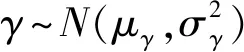
2.3 DPBNNMP目标函数
2.4 DPBNNMP算法

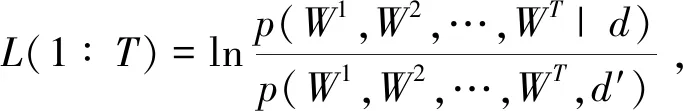
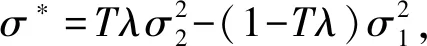
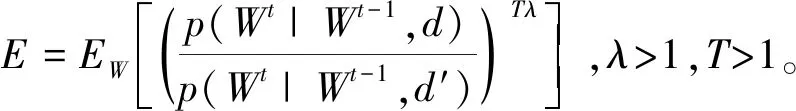
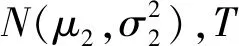
3 实验评估
3.1 实验设置



3.2 可用性分析
3.3 反向传播的隐私核算分析
3.4 前向传播的隐私核算分析
4 结束语

