PV-reduction of sunset topology with auxiliary vector

Bo Feng and Tingfei Li

1 Beijing Computational Science Research Center,Beijing 100084,China

2 Zhejiang Institute of Modern Physics,Zhejiang University,Hangzhou,310027,China

3 Center of Mathematical Science,Zhejiang University,Hangzhou,310027,China

4 Peng Huanwu Center for Fundamental Theory,Hefei,Anhui,230026,China

Abstract The Passarino—Veltman(PV)reduction method has proven to be very useful for the computation of general one-loop integrals.However,not much progress has been made when it is applied to higher loops.Recently,we have improved the PV-reduction method by introducing an auxiliary vector.In this paper,we apply our new method to the simplest two-loop integrals,i.e.,the sunset topology.We show how to use differential operators to establish algebraic recursion relations for reduction coefficients.Our algorithm can be easily applied to the reduction of integrals with arbitrary high-rank tensor structures.We demonstrate the efficiency of our algorithm by computing the reduction with the total tensor rank up to four.

Keywords: PV-reduction,sunset topology,loop

1.Introduction

Calculation of Feynman integrals at the multi-loop level is of great importance for both perturbation quantum field theory and particle experiments.The general strategy is to expand arbitrary integrals to finite simpler integrals (called Master Integrals)and then do the integration of master integrals only.Thus,tensor reduction of Feynman integrals is one of the critical steps for various realistic calculations in the Standard Model.There is a large body of research on one-loop reduction [1—25].For reducing multi-loop integrals,various ideas and methods have been developed.There are some works on two-loop tensor reduction for some special integrals[26—31],while an algorithm for the reduction of general Feynman integrals was proposed in [32—37].Among these methods,the Integration-By-Parts (IBP) method [36,37]is widely used and has been implemented by some powerful programs such as FIRE,LITERED,KIRA,etc [38—45].Although its popularity,the number of IBP identities grows very fast with the increasing number of mass scalars and higher rank of tensor structure,it will become a bottleneck when dealing with complicated physical processes.Even at the one-loop level,reducing a general tensor massive pentagon with the IBP method is difficult.Thus it is always welcome to find a more efficient reduction method.

PV-reduction [3]for one-loop integrals has played a significant role in general one-loop computations in history.However,when trying to generalize the method to higher loops,it becomes hard,and there are not many works in the literature.In [26,46],the tensor two-loop integrals with only two external legs are reduced to scalar integrals with the PVreduction method.However,an extra massless propagator appears.Integrals with new topologies have been introduced as master integrals to address the problem.This results against the intuitive picture: Reduction is achieved by removing one or more propagators from the original topology.Thus the reduction and master integrals should be constrained to the original topology and its sub-topologies.

Recently,we have generalized the original PV-reduction method for one-loop integrals by introducing an auxiliary vector R in[47,48].Our improved PV-reduction method can be easily carried out and compute reduction coefficients analytically by employing algebraic recursion relations.With these analytical expressions,one can do many things.For example,by taking limits properly,we can solve the reduction with propagators having general higher powers [49].When external momenta are not general,i.e.,the Gram determinant becomes zero,master integrals in the basis will not be independent anymore.We can systematically study their degeneration [50].

Encouraged by the results in [47,48],we want to see if such an improved PV-reduction method can be transplanted to higher loops.When moving to two loops,some complexities arise.The first is that we need to determine the master integrals.For one-loop,the master integrals are trivially known.For higher loops,the choice of master integrals becomes an art.With proper choice,one can reduce the computation greatly[51].The second is that when intuitively generalizing our method to two loops,we will meet the irreducible scalar products,which cannot be reduced.In fact,these two complexities are related to each other.To avoid unnecessary complexity,we will focus on the simplest nontrivial two-loop integrals,i.e.,the sunset topology in this paper.With this example,we will show how to generalize our new PV-reduction method to two loops.

This paper is structured as follows.In section 2,we briefly review our previous work on one-loop tensor reduction and discuss the main idea for the reduction of sunset integrals.In section 3,we derive recursion relations for sunset integrals using differential operators and the proper choice of the master integrals in our algorithm.In section 4,we demonstrate our algorithm successfully to sunset integrals with the total rank from one to four.In section 5,we give some discussions and the plan for further studying.Technical details are collected in the appendix.

2.Brief discussion of tensor reduction with auxiliary vector

In this section,we will give a brief discussion of the general idea of using the auxiliary vector R to do tensor reduction.We first review the method presented in[47,48]and then move to the two-loop sunset integrals.For the tensor reduction of a general one-loop integral (to avoid confusion,we denote Pjas propagators for one-loop integrals while Djfor two-loop integrals)

one can recover its tensor structure by multiplying each index with an auxiliary vectorRi,μi.Furthermore,we can combine these RitoR=xi Rito simplify the expression (2.1) to

The good point of using (2.2) instead of (2.1) is that we have avoided the complicated Lorentz tensor structure in the reduction process,while they can easily be retained using the expansion of R and taking corresponding coefficients of xi's.Since we are using dimensional regularization,we like to keep the D as a general parameter.For D=d-2∈,the master basis is the scalar integrals with n≤d+1 propagators,i.e.,the reduction results can be written as

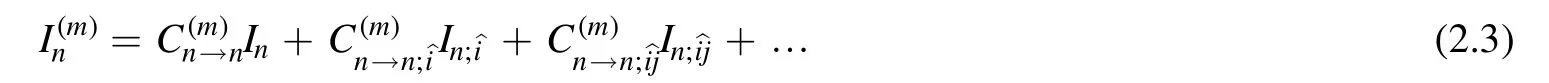
where we denoteas the integrals got by removing propagatorsPi1,Pi2,…,Piafrom In.For simplicity,we denote

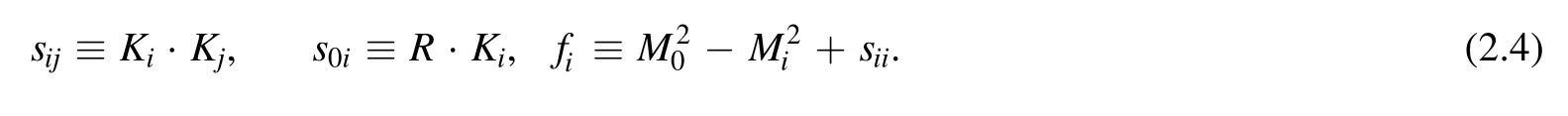
By the explicit permutation symmetry in (2.1),we only need to calculatewhile other reduction coefficients can be got by proper replacements and momentum shifting.With the introduction of auxiliary vector R in (2.2),one can expand the reduction coefficients according to their tensor structure

By acting two types of differential operatorson (2.2),we get the recursion relations for the expansion coeffciients

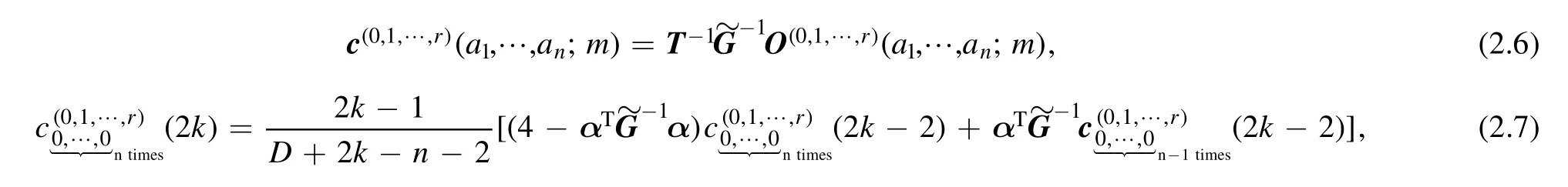
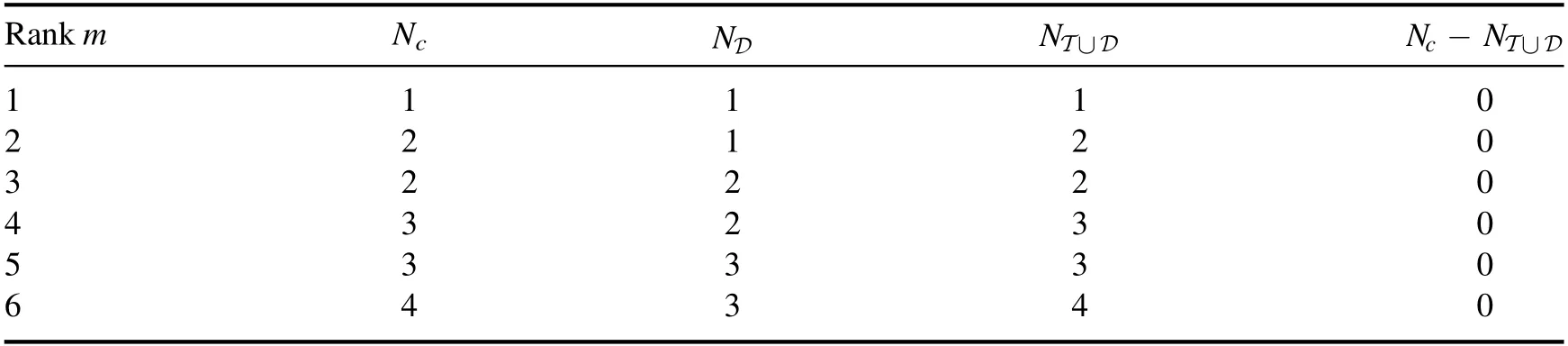
Table 1.Number of expansion coefficients and independent equations for tensor bubble.

is the n×n rescaled Gram matrix and T=diag(a1+1,a2+1,…,an+1)is a diagonal matrix.The vectors in the equations (2.6) and (2.7) are defined as

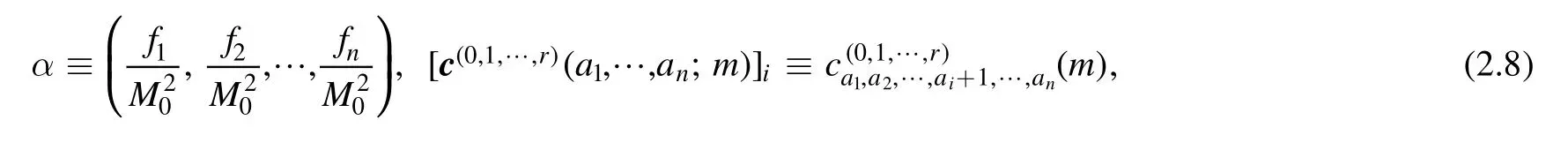
and

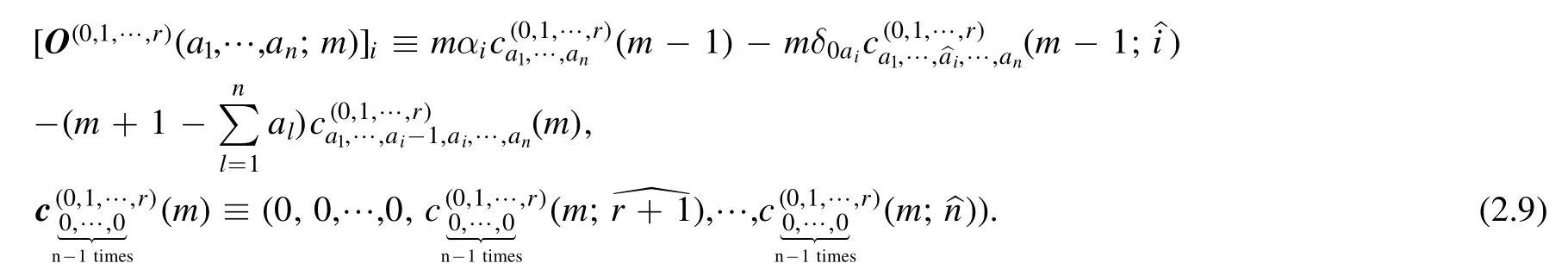
whereindicates to drop the index ai.With the known boundary conditions,one can obtain all reduction coefficients by applying the recursions (2.6) and (2.7) iteratively.

One important point of the above reduction method is that we need to use bothDiandT operators to completely fix unknown coefficients in (2.5).One simple explanation is that in (2.5) coefficients there are (n+1) indices (ai,i=1,…,n and rank m),so naively(n+1)relations are needed.A more accurate explanation is a little tricky.Let us take the bubble,i.e.,n=1 as an example.As shown in table 1,for rank m,there areunknown coefficients while the number of independentD-type equations isThus,only using theD-type operators we can fix all coefficients with odd rank m=(2k+1) by these known terms with lower rank m≤2k.However,for m=2k+2,Nc-ND=1,thus just usingD-type relations is not enough and we need to adopt theT operator to provide one extra independent relation.In fact,T provides more than just one relation,but other relations are not independent to these coming fromD and can be taken as the consistent check of the reduction method.

In this paper,we want to generalize our reduction method from one-loop to two-loop integrals.Again,with a simplified tensor structure,we define the general tensor integrals of sunset topology as5For simplicity,we denote the scalar integral Ia1,a 2, a3 ≡ .

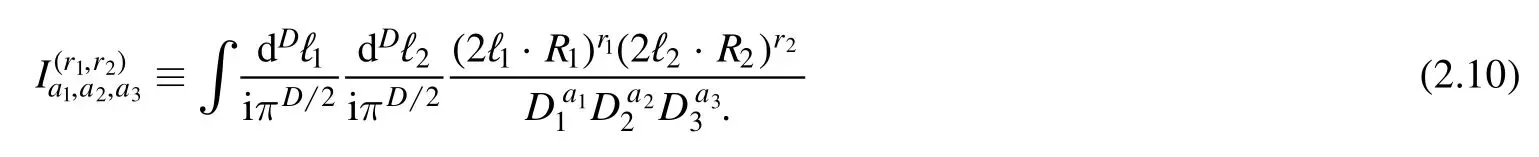
where the propagators are

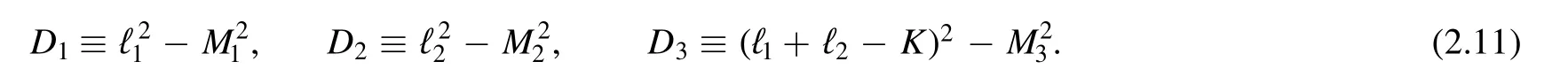
In this paper,we consider only the reduction with all ai=1.For ai≥2,one can use the same strategy presented in[49].For simplicity,we denote

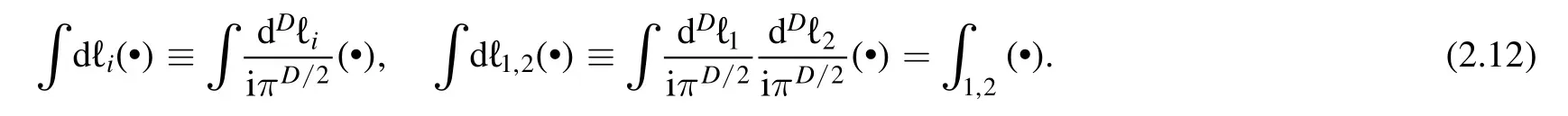
Similar to what we do for one-loop case,we can expand reduction coefficients according to their tensor structure6We will discuss the choice of master integrals J in section 3.3.

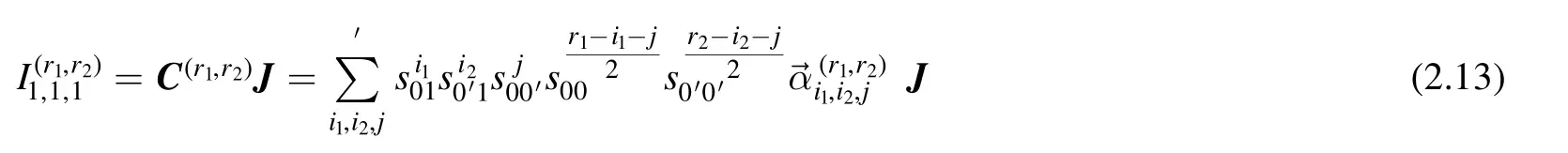
where we have written C,J to emphasize they are vector,while other kinematic variables are

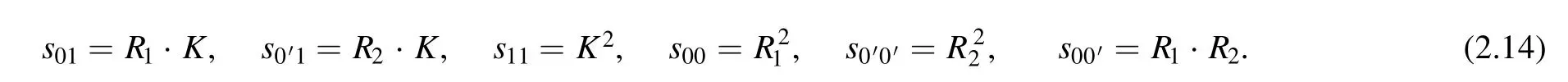
In(2.13),the expansion coefficientsare actually vectors with components corresponding to different master integrals Ji.The summation over indices{i1,i2,j}≥0 admits to the restriction 0≤(rl-il-j)/2 ∈N,l=1,2.We make the indices free by setting all=0for inappropriate indices throughout the paper,so we will drop the prime in other summations.Similar to the strategy for one-loop case,we solve expansion coefficients from lower rank levels to higher rank levels iteratively,where the rank level is defined as the total rank (r1+r2).

When we do the tensor reduction,we will reach the sub-topologies where one of the propagators in(2.11)is removed.For these cases,the integrals are reduced to the product of two one-loop tadpoles.Their tensor reduction has been solved in appendix B.To simplify notation,we denote

and their reductions are written as

In (2.13),there are five indices for the expansion coefficients,i.e.,i1,i2,j,r1,r2.With the experience from one-loop integrals,every index needs a recursion relation,so in total five kinds of differential operators are needed to give sufficient recursion relations.From the form of (2.2),we can construct threeT-type operators

By applying these operators on the tensor integrals (2.2),we produce combinationsℓ12,ℓ22,ℓ1·ℓ2in the numerator,respectively.Using the following algebraic decomposition

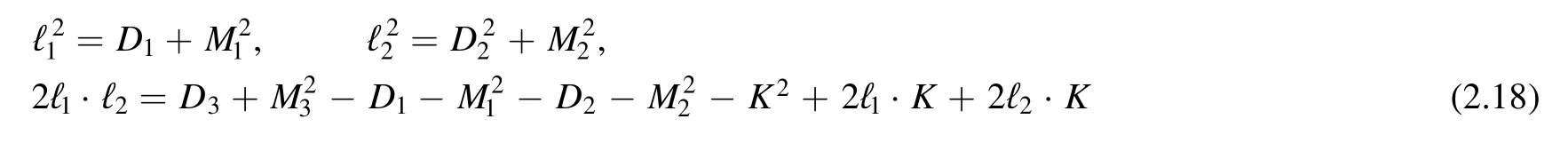
we can write the result as a sum of terms with one-lower or two-lower rank levels and terms for lower topologies,thus we can establish three recursion relations for these operators with expansion (2.13).

Having discussed the operatorsTi,it is natural to think about following twoD-type operatorsKμ·andKμ·.However,when acting on (2.2),it gives the combinations ℓ1·K and ℓ2·K.These two factors do not have simple algebraic decompositions like(2.18).Thus it is not so easy to find corresponding recursion relations.One key input in our paper is that the recursion relation ofD-type operators can be established if we consider the reduction of the sub-one-loop integrals first.As we will show,such a recursion relation is highly nontrivial and more discussions will be given later.

3.Recursion relations for tensor integrals of sunset topology

In this section,we first derive the recursion relations for expansion coefficients of threeT-type operators.Then we establish another two recursion relations ofD-type operators by reducing the left/right sub-one-loop first.As we will see,in the process,one needs to use a highly nontrivial relation of the reduction coefficients of tensor bubbles.Combining the recursion relations fromT-type andD-type operators,we get five relations.When using them to solve expansion coefficients,we find that not all coefficients can be fixed.It indicates that some integrals with nontrivial numerators should be recognized as master integrals.

After introducing two auxiliary vectors R1,R2,we can define differential operators(where we use the shorthand ∂A=)

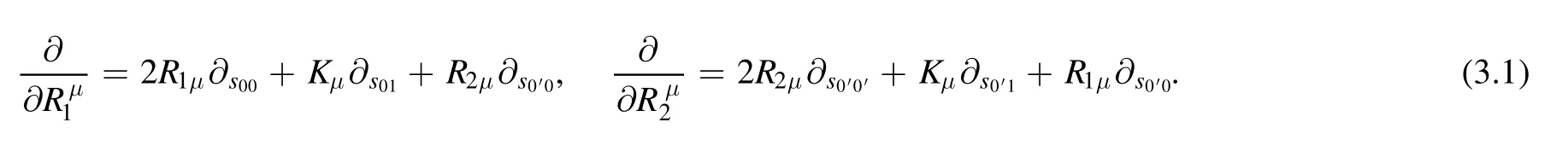
Using the two expressions and external Lorentz vectors,we can get the following Lorentz invariant combinations,i.e.,threeT-type operatorsT00,T00′,T0′0′defined in (2.17) and sixD-type operators

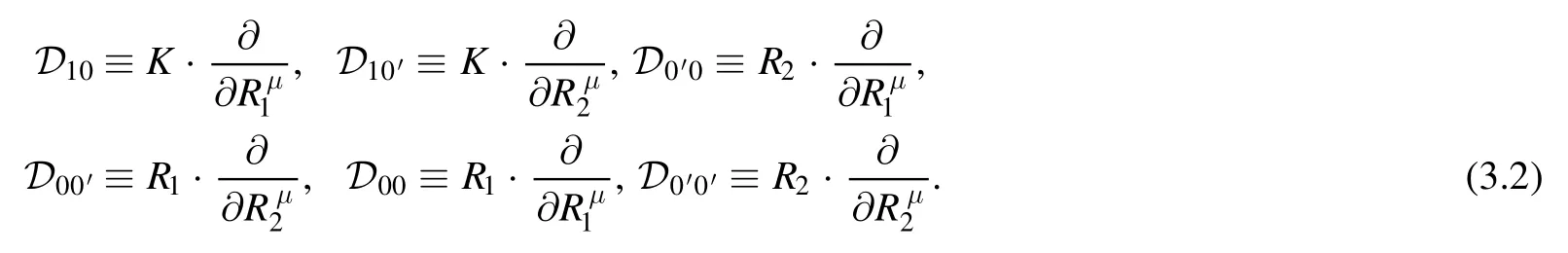
It is easy to use the definition (3.1) to find their action on reduction coefficients,for example,

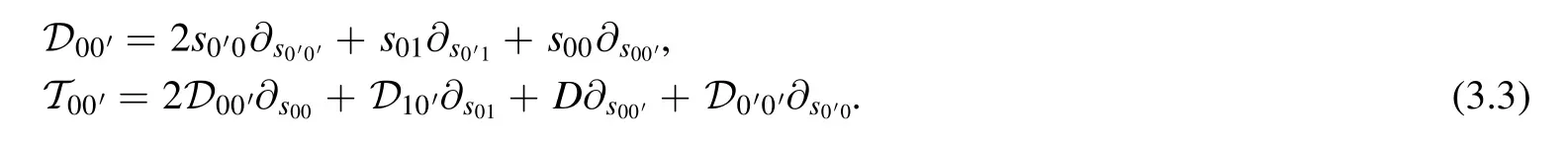
Employing them,we can write down recursion relations for expansion coefficients.

3.1.Recursion relations from T-type operators

Here,we derive the recursion relations for threeT-type operators.Let us start with the action ofT00.It is easy to check

by using the algebraic relation (2.18).Plugging the expansion (2.13) into both sides,we find the LHS of the equation is

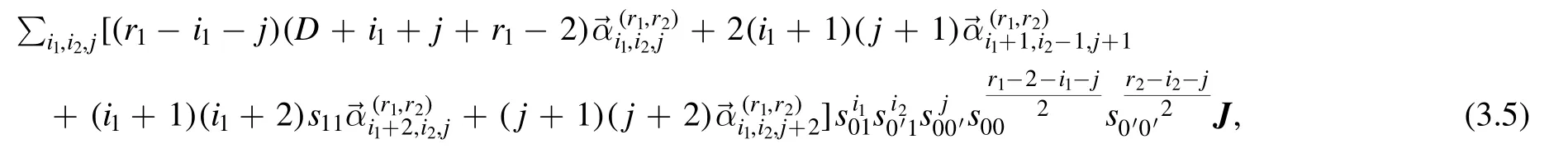
and the RHS is

where the definition ofhas been given in(2.16).Comparing both sides,we obtain the recursion relation for operator T00with r1≥2

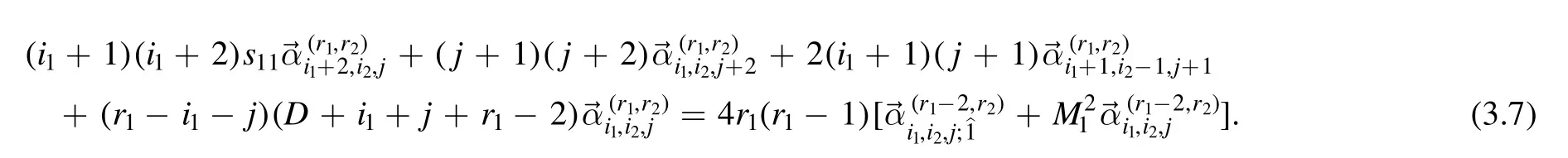
Similarly,one can derive the recursion relations for operatorT0′0′with r2≥2

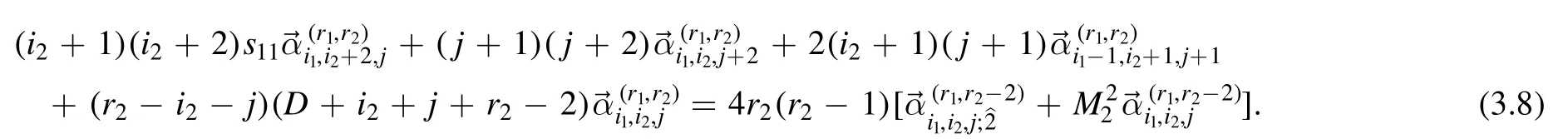
Finally,using the algebraic relation

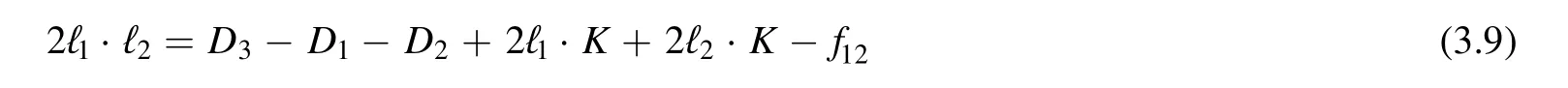
with

we derive recursion relations of operatorT00′for r1≥1,r2≥1 as

where we have used the shorthand

Employing the expansion (2.13),we find the LHS of (3.11) is

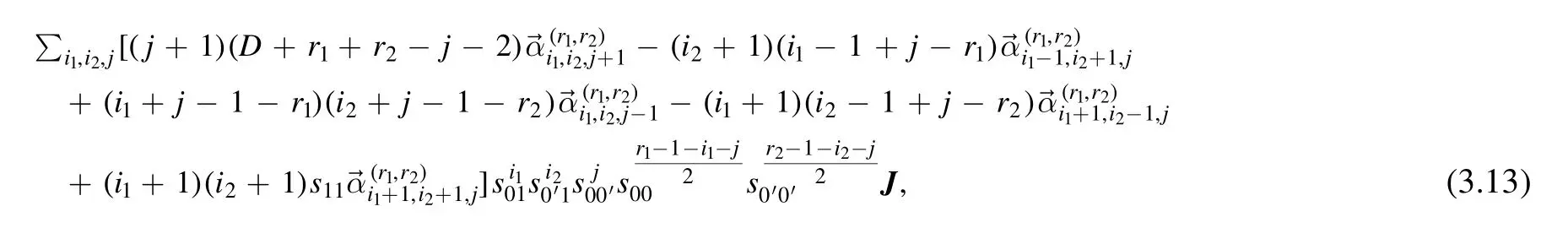
and the RHS is

Comparing both sides of equation (3.11),we have

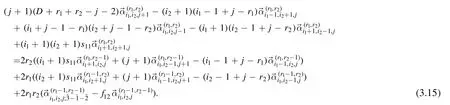
By now,we have obtained threeT-type relations(3.7),(3.8)and(3.15).As discussed in the introduction,these relations are not sufficient to solve all expansion coefficients iteratively.In table 2,we list the number of expansion coefficients (each vector→is counted as one coefficient)and the independent equations given by threeT-type recursions.Comparing two tables,we find the number of reminding unknown terms is universal:Nα-NT=1.So for each rank level r ≡(r1+r2)there reminds(r+1) unknown expansion coefficients.We need to find more relations to determine them.

3.2.Recursions relation from D-type operators

Having used theT-type operators,from the experience of one-loop integrals,it is obvious that we need to consider theD-type operators.Naively actingD10andD10′defined in(3.2)globally to(2.2),we get K·ℓiin numerator,which are irreducible scalar products and cannot be reduced further algebraically.How to get out of the deadlock?Let us look back to the two-loop integrals.Instead of doing the loop integration together,one can think it as two times integration:first,we integrate the ℓ1,then we carry out the integration of ℓ2.Using this idea,we can first do the tensor reduction of sub-one-loop integrals.Let us see what we can get.Let us start with the sub-one-loop integrals.From appendix A,the r-rank tensor reduction of one-loop bubbles

can be written as a summation of (r-1)-rank and (r-2)-rank bubbles as well as the contribution of tadpoles,whereP0≡ℓ2-M02,P1≡ (ℓ-K)2-M12.The striking point is that the Gram determinant K2only appears once in the denominator,i.e.,

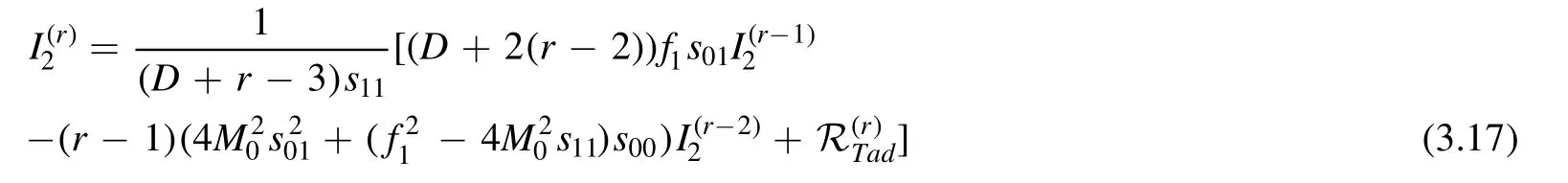
where we have defined

For example

where the pole of s11only appears in the overall factor.Now we insert(3.17)to the two loop integration by regarding propagator D1,D3as the propagators P0,P1,respectively,i.e.,we reduce ℓ1first

where we have defined

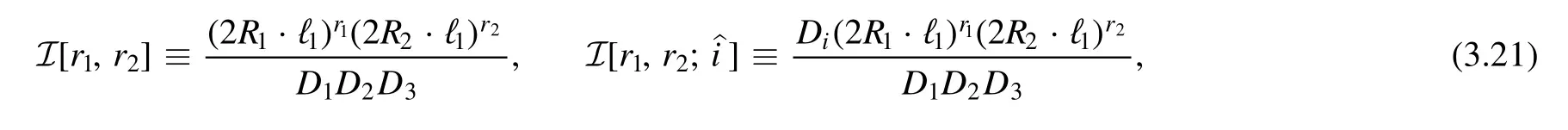
and

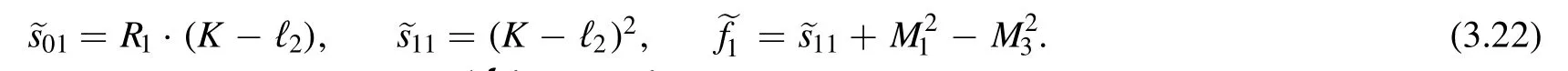
thus in (3.19) we have

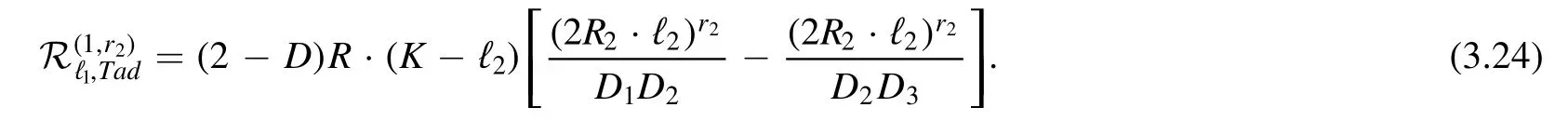
The appearancein the denominator in(3.19)causes some trouble since it depends on ℓ2,while the original sunset integrals do not have such a denominator.In the paper[46],they keep this factor and regard the two-loop integrals within the denominator as a new master integral.However,according to the reduction idea,such a solution is somewhat surprising since we expect that the reduction is achieved by removing original propagators.Thus,we should reach the original topology and its sub-topologies at last.

Since we want to keep the original reduction picture,we will try to get rid ofin (3.19).The idea is simple: one can multiply both sides with(D+r1-3)before integrating ℓ2and get

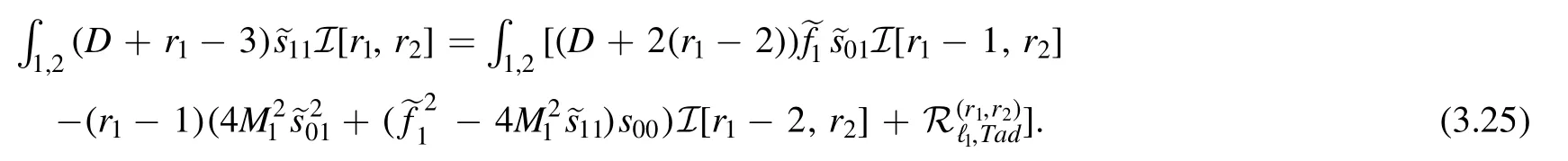
Writing

the LHS of the equation becomes (where we have suppressed the integral sign ∫1,2for simplicity)

where in the last term we replace the new tensor structure 2K·ℓ2by the action of differential operatorD10′on the basic form I [r1,r2+1](see(3.21)).One important point in(3.26)is that we have theD-type action on I [r1,r2+1],which is what we are looking for.

Now we consider the RHS of (3.25).There are three terms:For the frist term,using the expression ofin(3.22)and the rewriting in(3.26),we can write it as

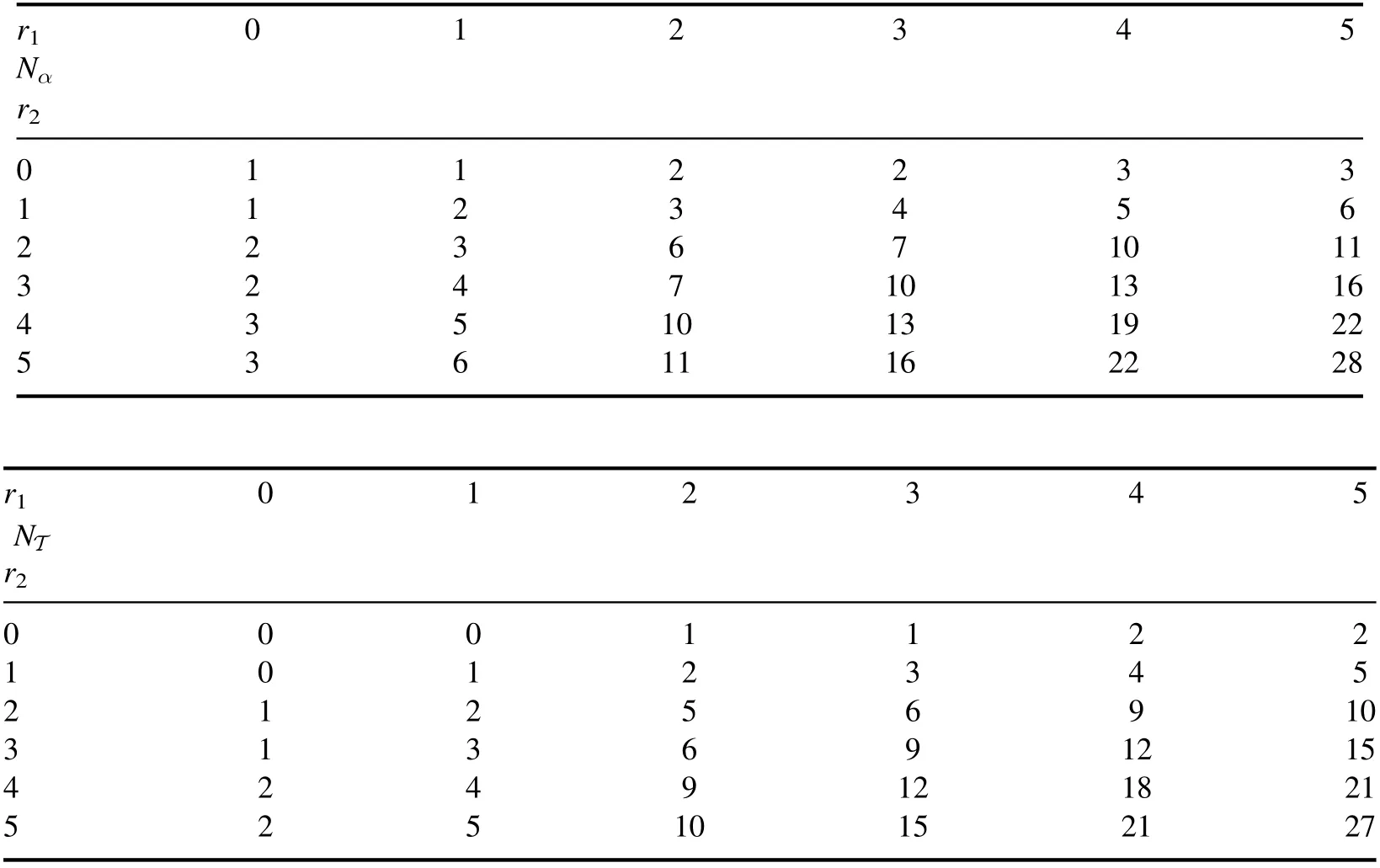
Table 2.Number of expansion coefficients (left) and independentT-type equations (right).

From the last equation in(3.28)one can see that the rank level of all terms will be less than(r1+r2+1),except the last term with rank level(r1+r2+1).For example,the termhas rank r1+r2.Similar analysis can be done for the other two terms in the RHS of(3.25),it is easy to see that they can be written as a combination of terms with rank level lower than (r1+r2+1).

Collecting all terms together,the RHS of (3.25) is

Rearranging (3.25),we arrive

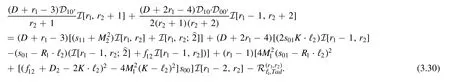
The recursion relation(3.30)is the wantedD-type recursion relation.The LHS of the equation can be written as a summation of expansion coefficients with rank (r1,r2+1),(r1-1,r2+2) of rank level (r1+r2+1) while the RHS can be written as a sum of expansion coefficients with rank level less than (r1+r2+1) and lower topologies.Thus,it is a recursion relation for rank level,instead of the explicit rank configuration (r1,r2).The reason is that under theD-type action,different rank configurations are mixed as at the LHS of (3.30).

By our recursion assumption,the RHS is considered to be known,and we can just write it as

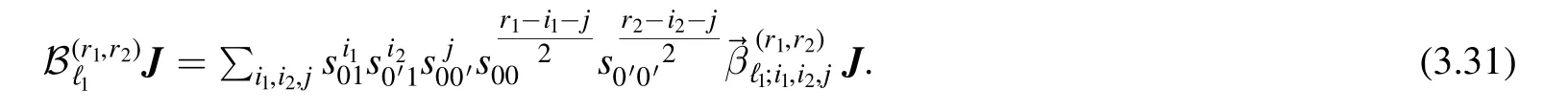
The expression of (3.31) for explicit r1,r2can be found in appendix C.Putting the expansion (2.13) into the LHS and after

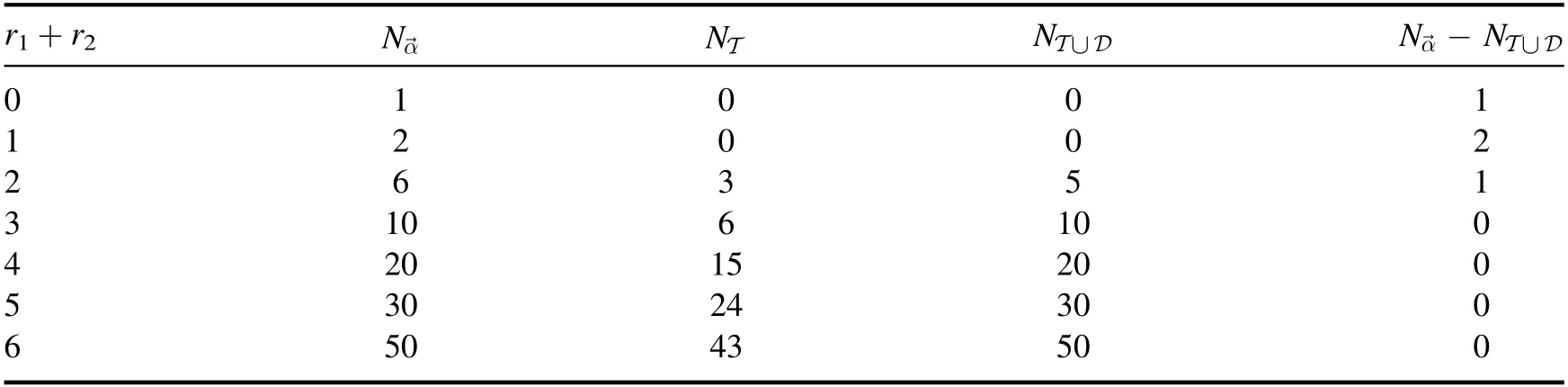
Table 3.Number of expansion coefficients and independent equations for several rank levels.

some algebra,finally we arrive at the algebraic recursion relation for unknown coefficients→

Similarly,if we reduce ℓ2first,we have

which is the dual expression of (3.30).Similarly,the lower-topology termin the equation can be got fromby regarding P0,P1as D2,D3,respectively,and multiplying withAgain,after plugging expansion(2.13)into the LHS of (3.33) and writing the RHS as

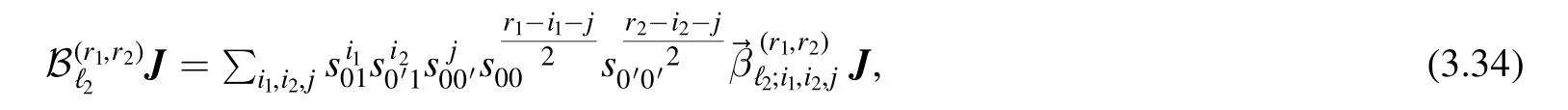
we will get another algebraic recursion equation for expansion coefficients which is dual to (3.32).

By now,we have derived twoD-type relations (3.30) and (3.33).Unlike theT-type relations which give a recursion relation for a particular rank configuration,D-type7will mix them: oneD-type relation (3.30) mixes ranks (r1,r2+1) and(r1-1,r2+2)while the otherD-type relation(3.33)mixes ranks(r1+1,r2)and(r1+2,r2-1).When using both types,one must do reduction level by level.As shown in table 3,one can solve all expansion coefficients for r1+r2＞2 by combining T-type andD-type relations while there are still four expansion coefficients to be determined,which indicates we need more relations for r1+r2≤2 level.As will be discussed later,this observation gives us a hint of the choice of master integrals.

3.3.Master integrals choice

Up to now,we have avoided giving the explicit choice of master basis in (2.13),since all recursion relations ofT-type and D-type are independent of the choice.The only constraint is that they cannot contain auxiliary vectors.However,as pointed out in table 3,the reduction for some lower-rank tensor integrals is not completely clear.

Let us consider them one by one.For rank level zero,it is the scalar sunset I1,1,1with no auxiliary vectors,so there are no differential operators that can act on it with nonzero results.Then we must regard it as a master integral,i.e.,J1≡I1,1,1.Next,we consider integrals with rank level one,for example,the integration

According to its tensor structure,we should have

The logic of the PV-reduction method is to solve B by multiplying K on both sides

Now a key point appears.Unlike the one-loop case,the contraction ℓ1·K cannot be written as the combinations of Di.Thus,we cannot solve B as a function of external momentum K,masses,and space-time dimension D only.This observation is well known,and it is related to the concept of the irreducible scalar product(ISP).For a given L-loop integrals with E+1 external legs,there areindependent scalar products involving at least one loop momentum.If there are N propagators Di,N scalar products can be written as the linear combination of Di's,which leadsirreducible scalar products.For one-loop integrals,we have L=1 and N=E+1,so there is no ISP,and every tensor integral can be decomposed to the scalar basis.But for two-loop integrals,there are nontrivial ISPs.Thus there are multiple master integrals for a given topology.For our sunset topology,we have L=2,E=1,N=3 and NISP=2,which are given by (ℓ1·K) and(ℓ2·K).With the above analysis and the irreducibility of the LHS of(3.37),it is natural to take the LHS to be a master integral

Similarly,we get another master integral

In table 3,there are two undetermined expansion coefficients for rank level ne.After taking J2,J3above to be master integrals,they can be solved easily as shown in the next section.

Then we consider the rank level two integrals,for example,

According to its tensor structure,we have

The only differential operator that can reduce the integral isT00′,which gives just one equation while there are two unknown expansion coefficients.As pointed out in table 3,there is only one undetermined expansion coefficient for rank level two.When combining the information of ISP,it is natural to take the integral obtained by acting withD10D10′,i.e.,

to be another master integral.In fact,another two choices,i.e.,

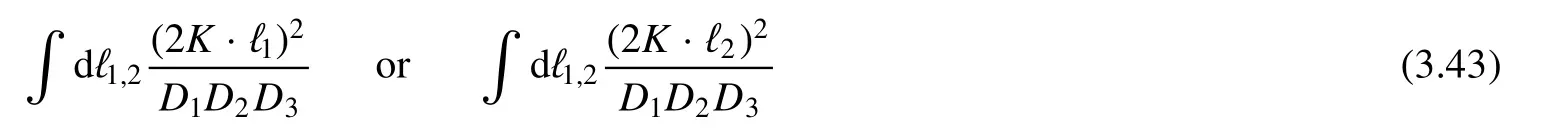
should be equivalently fine.

Having chosen master integrals for sunset topology,we discuss the master integrals for lower topologies.These lower topologies are obtained by removing one of the sunset’s propagators,and the resulted topology is the product of two one-loop tadpole integrations.For one-loop integrals,we know the basis is the scalar integrals,thus it is easy to see that we have the following three master integrals

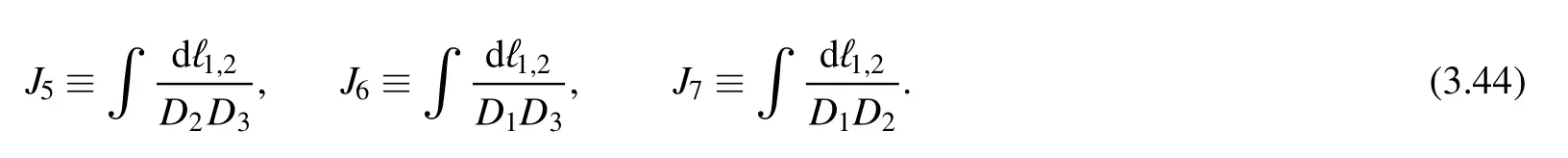
One technical point is that the standard form of J5,J6should be written with the proper momentum shifting.For example,

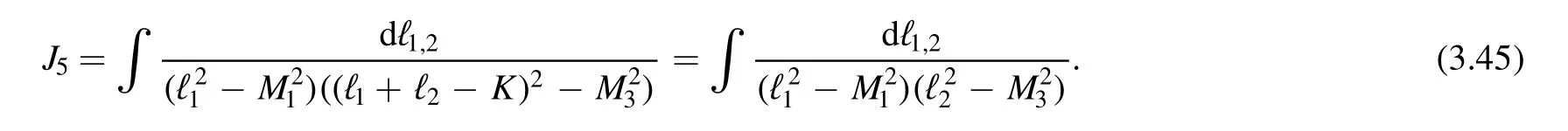
Our discussion on ISP and the choice of basis hints that the number N of master integrals is related to the number Nispof ISP when the masses and momenta are general.Another point is that when using the FIRE to do the reduction,it will take a different master basis.In appendix D we will present the non-degenerate transformation matrix between these two basis,thus our choice of basis is legitimate.

Before ending this subsection,let us discuss briefly the number of master integrals when the kinematics and masses are not general,for example K2=0 or M1=M2.For K2=0,but M1,M2,M3are different,there are only four master integrals J1,J5,J6,J7and J2,J3,J4will be decomposed to a linear combination of them.We can get the proper reduction coefficients by taking the limit carefully,as discussed in[50].If M1=M2≠M3,but K2≠0,we will have J5=J6and J2=J3,i.e.,there are only five master integrals.If the reduction coefficients are not singular under the limit M1→M2,we just add reduction coefficients together,i.e.,c2J2+c3J3→(c2+c3)J2.If the reduction coefficients are singular under the limit,we need to expand J3by other master integrals with expansion coefficients as the Taylor series of (M1-M2) as presented in [50].

4.Examples

Having laid out the general reduction frame in the previous sections,we present examples to demonstrate our algorithm.In this section,we will give the exact reduction process for the rank levels from one to four.The full expansion of coefficients is collected in appendix E and an attached Mathematica file.

4.1.Rank level one

Having chosen seven master integrals Ji,we start the reduction for tensor sunset with rank level one.There are two integrals

Due to the total rank being less than 2,bothT-type andD-type recursions(3.30)and(3.33)cannot be used.However,we can apply operatorsD10andD10′on the two integrals,respectively.For example,the action ofD10on the integralgives

where we have defined a constant vector

The reason one can obtain the relation is that we choose J2as a master integral.

For this case,the expansion (2.13) is

Plugging it into the LHS of (4.2),we have the relation

Comparing both sides,we can easily solve

Similarly,we have

4.2.Rank level two

There are three integrals.By the expansion (2.13),we have

Let us start from the rank (1,1).The onlyT-type recursion relation is given byT00′.Using (3.15),we have

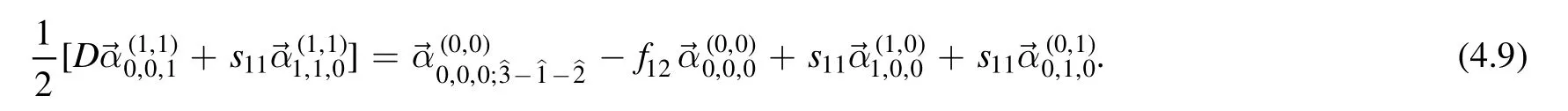
Then we consider the action ofD10D10′

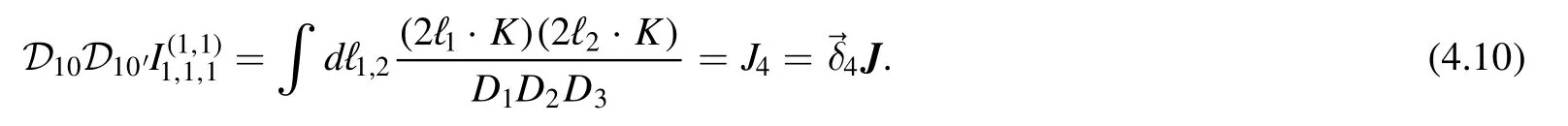
where={0,0,0,1,0,0,0}.Using the expansion (4.8),we find the LHS is

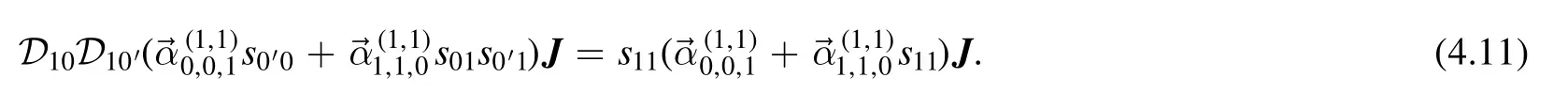
Plugging it into (4.10),we have

Combining (4.9) and (4.12) we can solve out

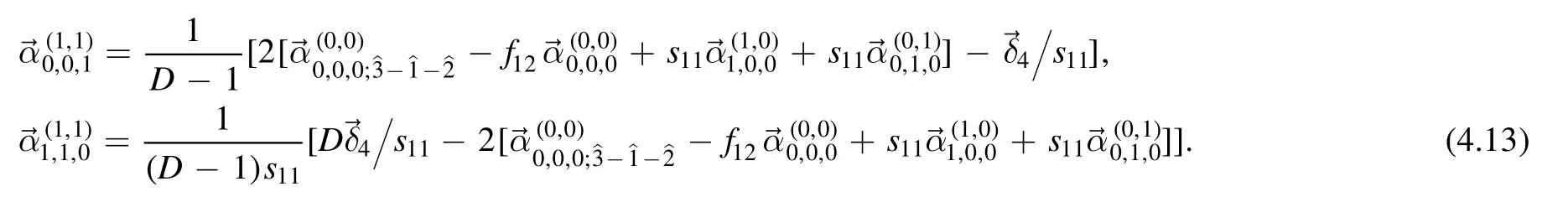
Using the results of lower rank levels and lower topologies,we get

From the above analysis,one can see the reason for taking master integral J4as discussed in the previous section.

Next,we consider the rank (2,0).The onlyT-type relation is given byT00.Using (3.7) we have

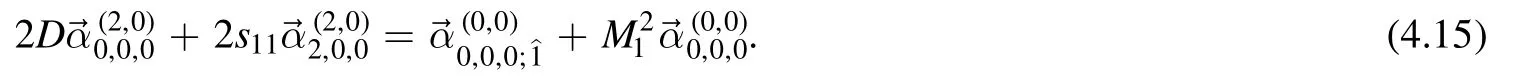
TheD-type relation (3.33) mix the rank (2,0) and the (1,1) and give

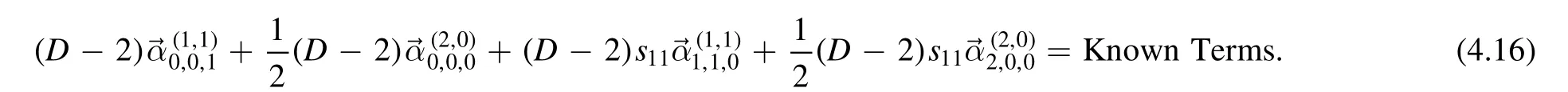
Combining (4.16) and (4.15) and using (4.14),we can solve

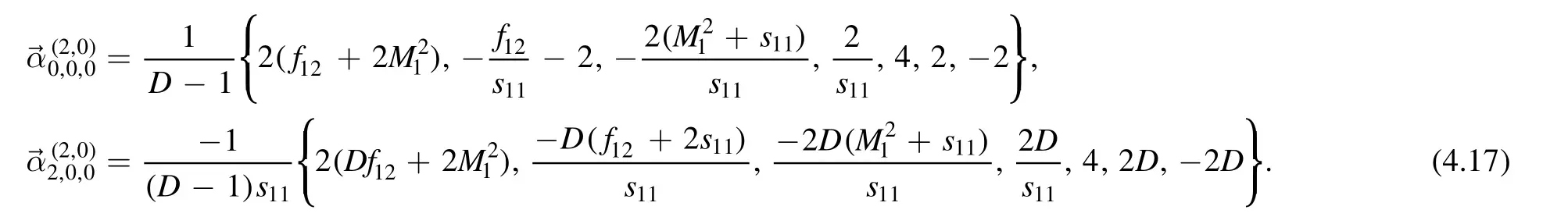
By proper replacement,we have

4.3.Rank level three

There are four rank configurations and the expansion (2.13) is

We list 14 linear equations ofT-type andD-type relations for these ten expansion coefficients.There are only ten of them are linearly independent and the other four extra can be used as the self-consistence check.We listT-type equations first,

·T-type relations

— rank (3,0)

— rank (2,1)

— rank (1,2)

— rank (0,3)

These six independent equations restrict the number of unknown expansion coefficients to 4.For every rank configuration,the number ofT equations is always one less than the number of expansion coefficients,which agrees with our discussion.

Now we consider theD relations for rank level three,which are represented by four arcs in figure 1,where two red arcs for reducing ℓ1first and the other two orange arcs for reducing ℓ2first.We list them below:

·D-type relations by reducing ℓ1first

— Mix rank (0,3) and (1,2)

The reason for having two equations is that even with the removal of one R2byD operator,we are still left two different tensor structures,i.e.,s0′0′and.

— Mix rank (1,2) and (2,1)

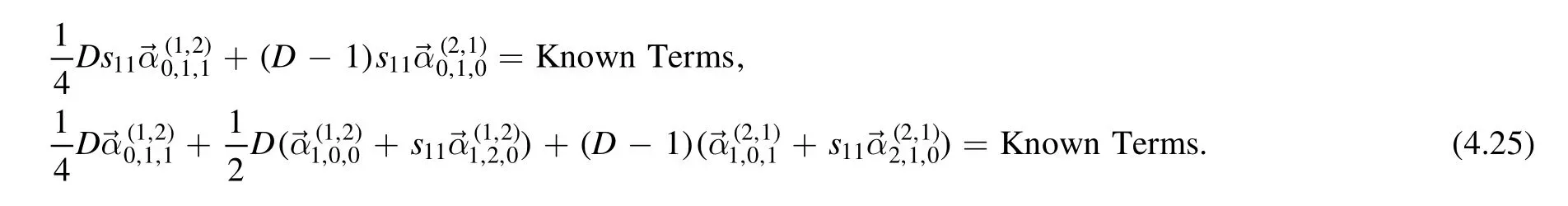
·D-type relations by reducing ℓ2first

— Mix rank (3,0) and (2,1)

— Mix rank (1,2) and (2,1)

One can pick ten independent equations from the relations above and solve all expansion coefficients.Denoting

we have linear equations=bwith matrix W

and the known vector b which corresponds to lower rank level and lower topologies.We solve these linear equations and present the final results in appendix E.

4.4.Rank level four

There are five rank configurations and the expansion (2.13) is

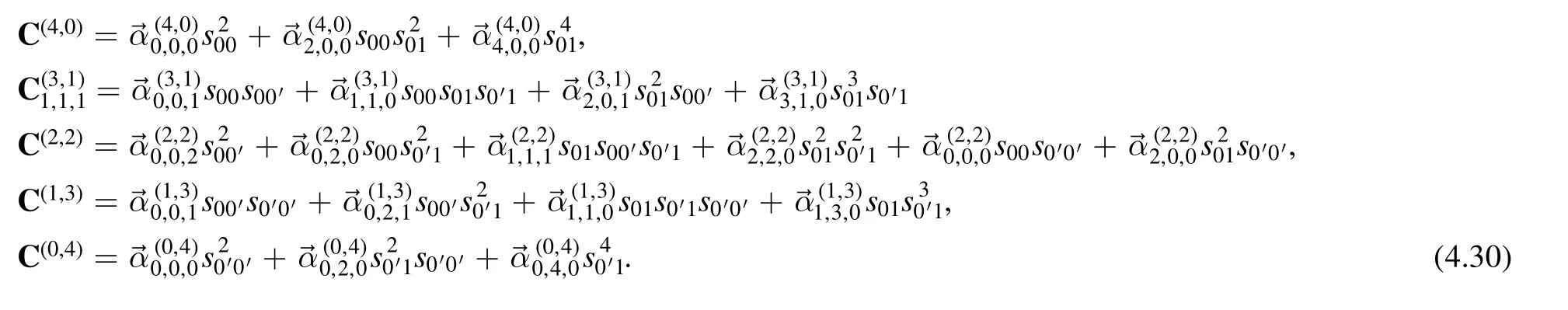
One can get 34 linear equations fromT-type andD-type relations for these 20 expansion coefficients.We can pick 20 independent equations among them.There are 18T-type equations

For 16D-type equations,we have

· reducing ℓ1first

· reducing ℓ2first

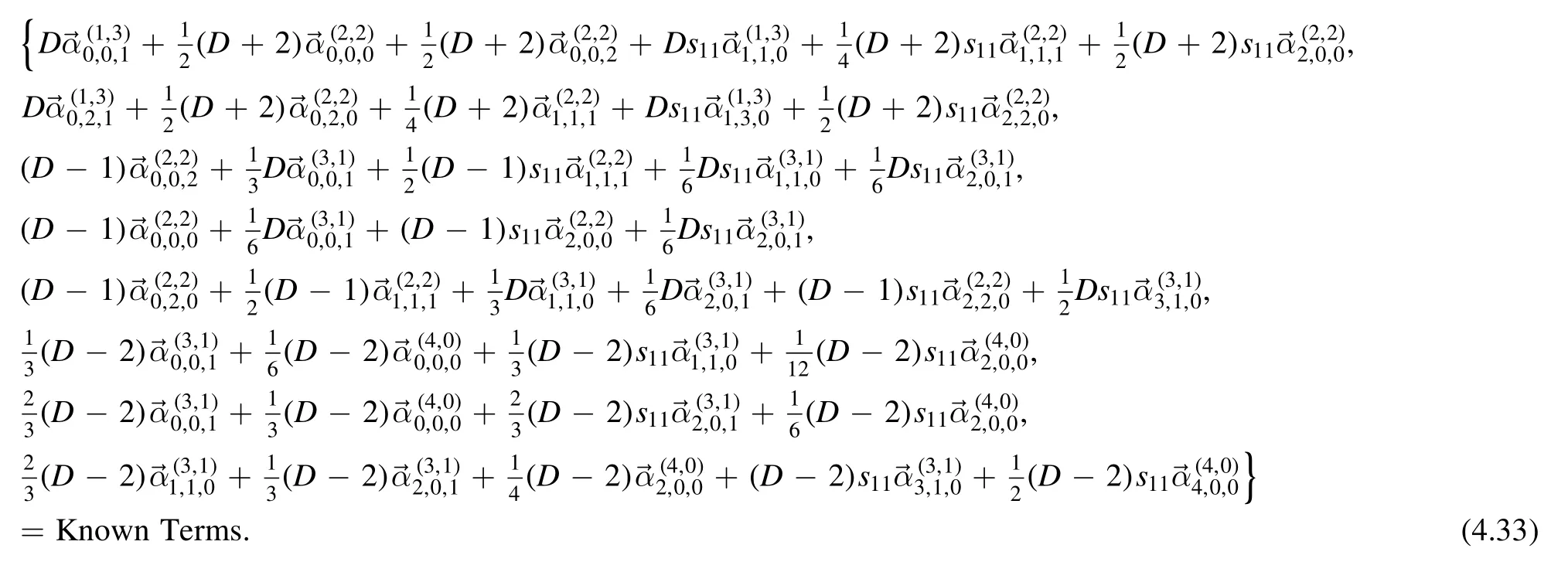
Picking 20 independent equations,we can solve all expansion coefficients of rank level four.Since its expression is long,we present them in an attached Mathematica file.All coefficients have been checked with the analytic output of FIRE[38,39,41].

Before ending this section,let us summarize the algorithm to reduce tensor integrals of sunset topology to the master basis.The number of expansion coefficients for a particular rank level r is given by

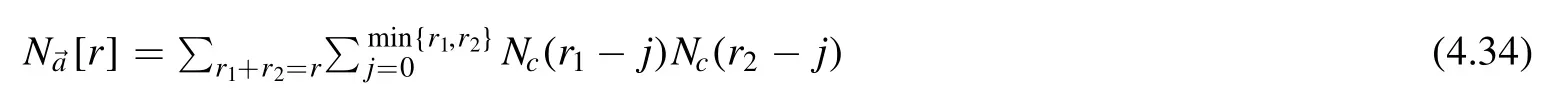
whereNc(m)=+1is the number of expansion coefficients for a one-loop rank-m tensor bubble.The recursion procedure can be nicely represented in figure 1.

5.Conclusion and outlook

In this paper,we have taken the first step in generalizing our improved PV-reduction method with auxiliary vector R to twoloop integrals,i.e.,we have carried out the tensor reduction for the simplest sunset topology.For two-loop integrals,theT-type relations can be established straightforwardly,while theD-type relations are rather nontrivial.We need to consider the reduction of its sub-one-loop integrals first.Combining the two types of relations,one can solve all expansion coefficients with the proper choice of master basis.

One of our motivations for the paper is to find an alternative method for higher loop tensor reduction other than the IBP method.Comparing these two methods,one can find some similarities.All IBP relations are generated by following six primary relations·Kjwith i=1,2 and Kj=(ℓ1,ℓ2,K).Similarly,in our algorithm,there are also six operatorswith i=1,2 and=(R1,R2,K).The one-to-one mapping between these two types of manipulations seems to hint at a deep connection between these two methods although we are not clear at this moment.As pointed out in the paper,in our algorithm we have avoided the appearance of higher power propagators,thus the number of equations one needs to solve is much fewer than that using the standard IBP method.However,in[52]an idea has been suggested to avoid the higher power of propagators in the IBP method.It will be interesting to see if such an idea can be used in our algorithm.

There are several interesting questions coming from this work.The first one is that,in section 3,we have discussed the choice of master integrals to be evaluating the ISP.We hope that for arbitrary two-loop or higher loop integrals with general masses and momenta K,one can determine the master basis from this perspective.

The second question is the following.As emphasized several times,the nontrivialD-type relations depend crucially on the reduction relation (3.17) of one-loop integrals.We have tested the reduction of triangles and found similar reduction relation also holds for several examples.We find such a reduction relation holds for general one-loop integrals with the proof being presented in [50].

The third problem is obvious.In this paper,we focus on the sunset topology.There are other topologies for two-loop integrals.One needs to check if the algorithm present in this paper can be generalized to these cases.With results from higher topologies,we can reduce sunset with propagators having higher power using the idea given in[49].We hope to give a positive answer to these interesting questions in our future work.

Acknowledgments

This work is supported by Chinese NSF funding under Grant Nos.11935013,11947301,and 12047502 (Peng Huanwu Center).

Appendix A.The reduction of one-loop tadpoles and bubbles

In this part,we will collect the reduction of one-loop tensor tadpoles and bubbles,which have been extensively used in this paper.

For the one-loop rank r tensor tadpole

the reduction result is given by

where

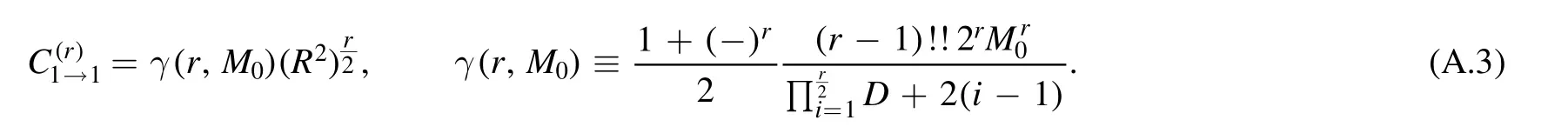
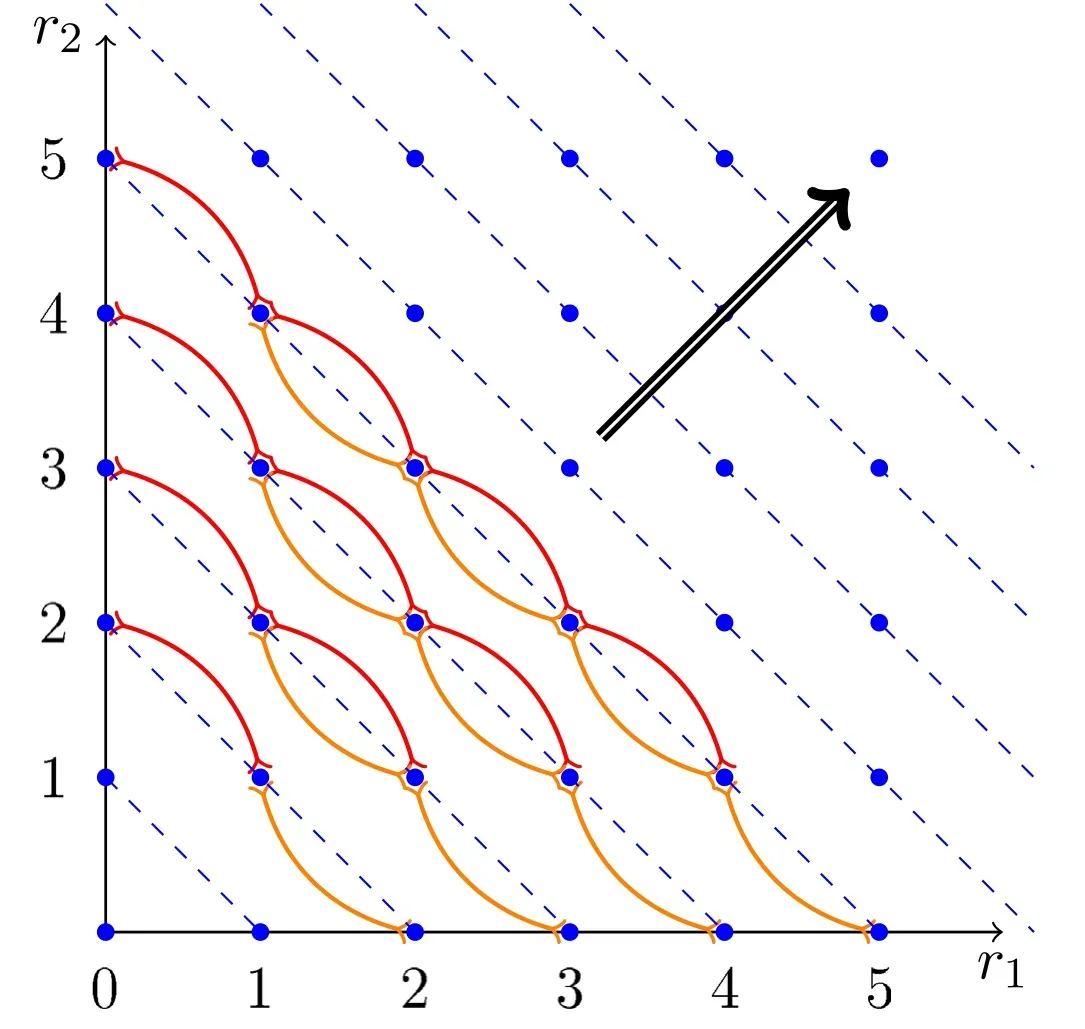
Figure 1.Algorithm for tensor reduction of sunset topology,where every point represents a particular tensor configuration (r1,r2).After using theT-type relations,only one unknown coefficient is left for each point.To determine the last unknown piece,we need to useD-type relations to relate different tensor configurations with the same rank level.We have used the red lines to represent relations coming from D-type relations for ℓ1,and orange lines,for ℓ2 respectively(here we drawD-type relations for r1+r2≤5).Each line provides a nontrivial relation among unknown coefficients.One can see that for rank level r≥3,the number of lines is equal or larger than the number of unknown coefficients,thus they will give enough equations.

For the one-loop rank r tensor bubble

the reduction result is given by

where

If we collect these coefficients into a listusing the notations

we will have the following results:

· For the rank r=1:

· For the rank r=2:

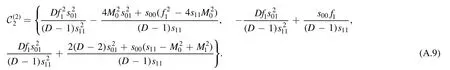
For our application,we have separated terms according to the power of pole s11.One crucial point is that we can writeC(22)as the combination of lower-rank coefficients and the contributions from lower topologies (tadpoles)

· For the rank r=3:The three reduction coefficients are

By matching the terms with different powers of pole s11,we can expandC(23)as

One technical point of expansion (A.12) is that there are other different expansions,for example

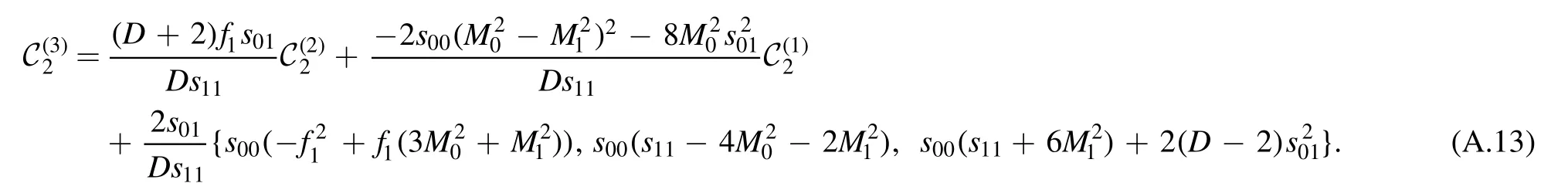
The difference between (A.13) and (A.12) is whether the coefficient of the bubble in the last term is zero or not.For simplicity of application,we prefer the form of(A.12).The choice of bubble coefficient to be zero for the remaining term has fixed the expansion uniquely.

· For the rank r=4:After some algebra,we have

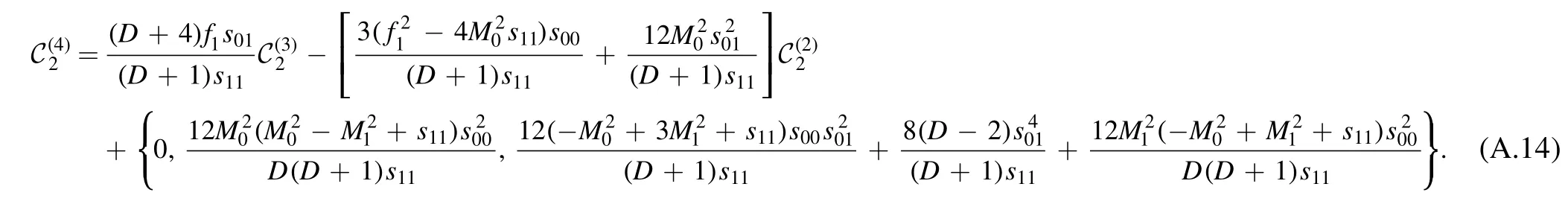
· For the rank r=5:

From these examples,one can observe the general expansion for any rank r ＞0 to be

Let us start fromD-type recursion relations,i.e.,the differential equation generated byD1for the bubble.Acting with K∂Ron both sides of (A.12) and using 2K·ℓ=D0-D1+f1.The LHS is

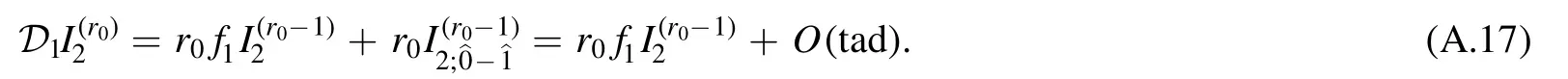
The termcan be reduced to scalar tadpole without any poles from Gram determent s11,and for simplicity,we just denote the contribution of tadpole topology as O(tad).The RHS becomes

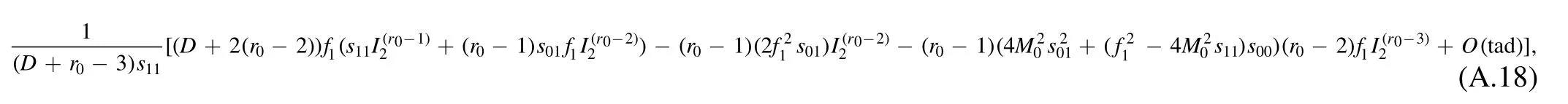
To require (A.18) to be equal to (A.17),one needs the following equation

which is just (A.16) with r=r0-1.

Then we consider theT-type recursion.Acting withT on the LHS of (A.16),we get

while acting on the RHS we get

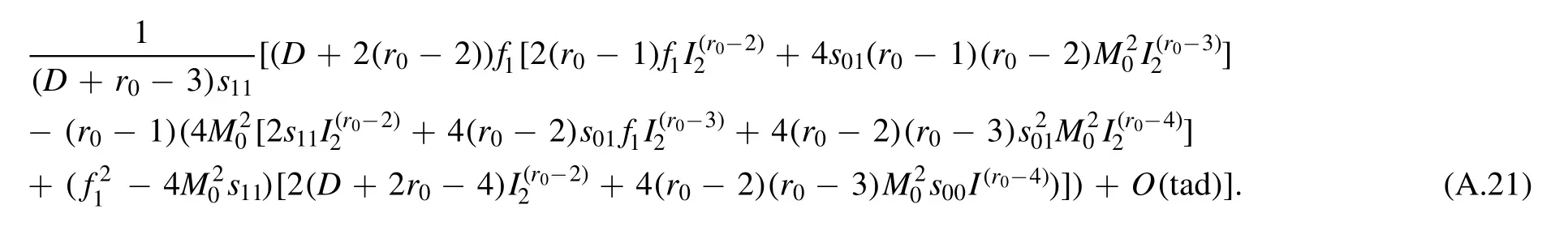
One can prove (A.20) is equal to (A.21) by employing the recursion relation (A.16) for rank r0-2.

One crucial point of the above proof is that,in principle,one can establish recursion relations offor general r.Thus we can solve it and get the complete relation (A.16) with explicit expression for.This result will give another recursive way to analytically compute reduction coefficients,which may be more efficient than the one given in [48].Furthermore,knowing,one may write down the analytic expression ofin(3.32)and its dual form.Then we can get the algebraic recursion relation for all coefficients for any rank level,just like what has been done in[47,48].It is obvious that with higher and higher rank levels,all available programs,like FIRE,Kira,Reduce [40—43]will become harder and harder to handle analytically.However,the method proposed in this paper can still work with fewer efforts.

Appendix B.Reduction of lower topologies

Here we give the reduction results for integrals got by removing the ith propagator in the tensor sunsets,i.e.,.We denote

from which we can easily read outin(B.1).Forbecause the subtlety discussed in(3.45),we need to shift ℓ1in the numerator.The computation details are:

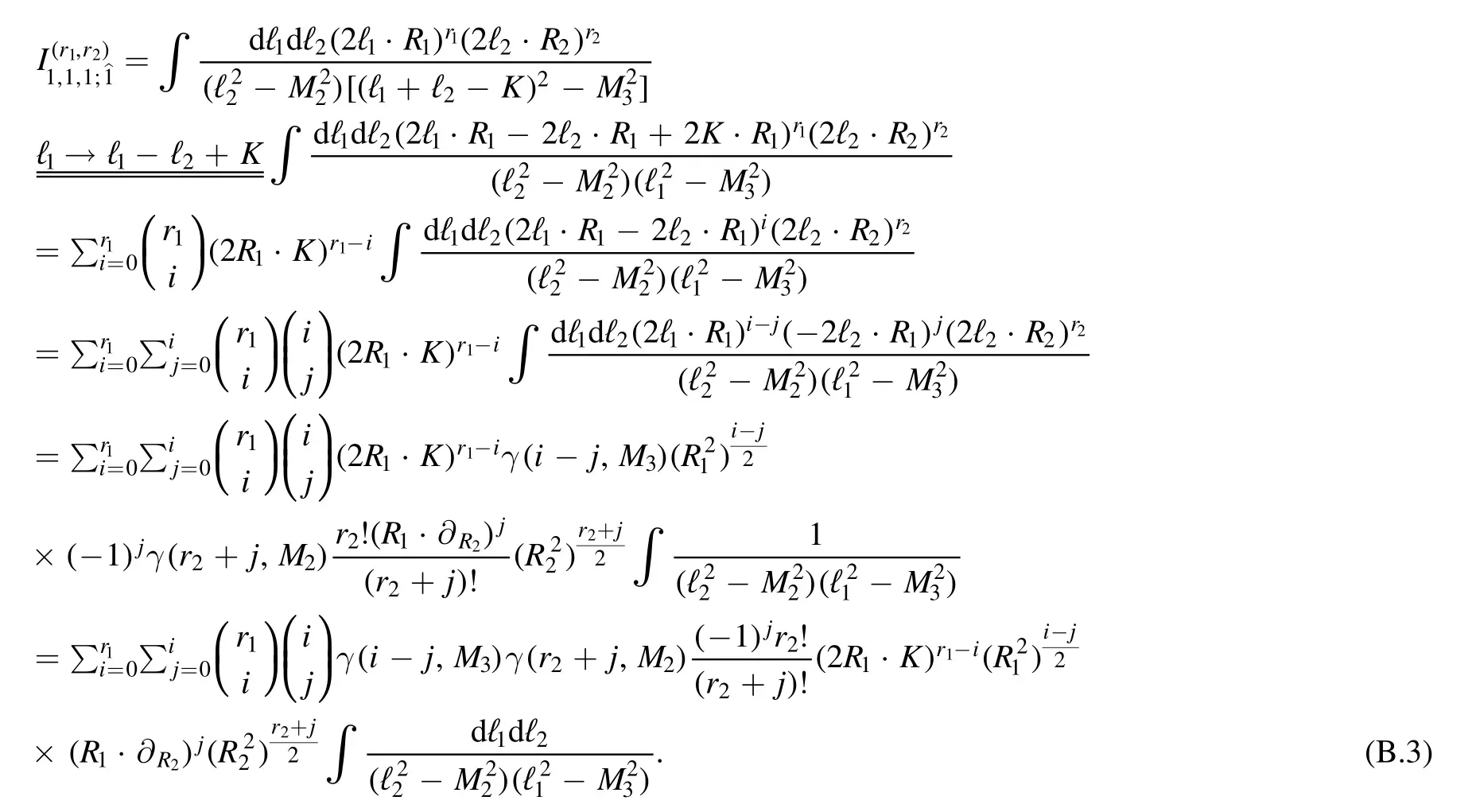
Similarly,we have

Appendix C.Lower rank/topology terms in D-type relation

To write downD-type recursion relation for given r1,r2,we need calculatedefined in(3.31).Here we list some results.For the rank (1,r2) and (r1,1),the general forms are

One can also write down expressions for(2,r2),(3,r2)etc.The expression will become longer and longer.Since in examples the rank level is up to four,we just list the terms we used in the examples

Appendix D.Transfer matrix between tensor MIs and scalar MIs

In section 3.3,we have discussed the choice of master basis.The basis chosen by FIRE6 is

and the basis used in this paper is

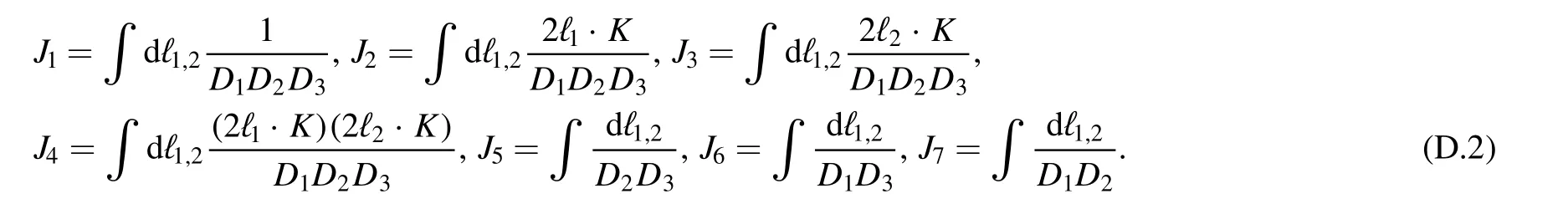
The transform matrix J=TF is

One can check that with general masses and K,it is non-degenerate.

Appendix E.Results

Here we collect the reduction results from rank levels one to three for reference.It is too long to write in text form for rank level four,so we collect them in an attached Mathematica file.

· rank r1+r2=1

· rank r1+r2=2

· rank r1+r2=3

There are ten expansion coefficients for rank-3 level.