Driving potential and fission-fragment charge distributions
Yuan Su,Min Liu,2 and Ning Wang,2
1 Department of Physics,Guangxi Normal University,Guilin 541004,China
2 Guangxi Key Laboratory of Nuclear Physics and Technology,Guilin 541004,China
Abstract We propose an efficient approach to describe the fission-fragment charge yields for actinides based on the driving potential of the fissioning system.Considering the properties of primary fission fragments at their ground states,the driving potential,which represents the potential energies of the system around scission configuration and closely relates to the yields of fragments,can be unambiguously and quickly obtained from the Skyrme energy-density functional together with the Weizsäcker–Skyrme mass model.The fission-fragment charge distributions for thermal-neutron-induced fission and spontaneous fission of a series of actinides,especially the odd–even staggering in the charge distributions,can be well reproduced.Nuclear dynamical deformations and pairing corrections of fragments play an important role in the
Keywords: nuclear fission,fragment charge distribution,driving potential,nuclear deformation,energy density functional
1.Introduction
Nuclear fission is a field of very intense studies for more than half a century[1–7].One of the most interesting characteristics of neutron or heavy-ion induced fission is the huge difference in the mass and charge distribution of the fission fragments for different nuclei.The investigation of the fission fragment yields is of great importance not only for nuclear engineering but also for understanding the fission process,testing nuclear models and exploring the role of fission recycling as well as the structure of extremely neutron-rich nuclei for the study of r-process in nuclear astrophysics[8–10].It is yet not very clear,until now,how the original compound nucleus is transformed into a variety of different fragments.It is qualitatively thought that the shell effect plays a role in the double-humped distribution for the fission of some actinides.Accurate predictions for the fission fragment distribution especially the charge distribution of actinides including the odd–even staggering [11]are still urgently required.
To describe fission dynamics and fission barrier,some microscopic or semi-empirical approaches,such as the Skyrme Hartree–Fock models[12,13],the covariant density functional theory [14,15]and the macroscopic–mircoscopic models[1,5,16,17],were established for calculating the potential energy surface(PES) of a fissioning system from ground state deformation to scission configurations.With the aid of modern computers,the fission barriers of nuclei can be successfully reproduced with a deviation of about one MeV[1,14,15],and the fission fragment distributions can be roughly reproduced based on the five-dimensional PES from the macroscopic–microscopic model [5].The calculations of multi-dimensional PES are time-consuming since millions of wave equations for strongly (triaxial) deformed nuclear potentials need to be solved for obtaining the single-particle levels of the system at different deformation configurations.Furthermore,the determination of the model parameters especially the strength of the spin–orbit interaction and that of the pairing force from the saddle to scission is difficult in the traditional PES calculations,which could reduce the predictive power of the models for describing the yields of fission fragments.It is therefore necessary to develop an alternative more efficient method for studying fission around scission and post-scission movements.
To describe the competition between quasi-fission and complete fusion of super-heavy systems,the di-nuclear system(DNS)concept was successfully proposed[18–22].In fact,the microscopic shell structure and even–odd effect can be involved in the potential energy surface of DNS.According to the DNS concept,each fission fragment around the scission point retains its individuality in the evolution of the DNS.In [23],it was found that the valley of the driving potential for the mass number of heavy fragments locates at 140 for neutron-induced fission of235U,which is in good agreement with the peak of measured mass distribution.It is therefore interesting to investigate the charge yields for the fission of actinides based on the corresponding driving potentials.
In this work,we attempt to study the yields of fission fragments based on the DNS concept.Different from the traditional studies based on the whole potential energy surface of a fissioning system from the ground state to the scission point,we focus on the potential energy surface around scission configuration.We would like to study the influence of nuclear structure effect on the yields of primary fission fragments especially the odd–even staggering in the charge distribution for binary fission of actinides at low excitation energies.
2.Driving potential of a fissioning system
The total potential energy of a fissioning system around scission is written as

where E1and E2denote the potential energies of the light and heavy fission fragments respectively,which are functions of nuclear deformations.V(β→,R) denotes the interaction potential between two fragments with the center-to-center distance R,which is obtained with the Skyrme energy-density functional plus the extended Thomas–Fermi (ETF) approximation [24].In the Skyrme energy-density functional approach,the total binding energy of a nucleus can be expressed as the integral of the energy density functional which is a function of nuclear densities of protons and neutrons under the ETF2 approximation[25].In our calculations,the nuclear central densities and surface diffuseness for a certain nucleus (or fragment) are firstly determined by using the restricted density variational method and taking the neutron and proton density distributions as spherical symmetric Fermi functions [24].Then,we introduce nuclear deformationsβ→in the radius parameter,remaining the central densities and surface diffuseness of the nucleus (or fragment)unchanged,to consider the influence of nuclear deformations on the interaction potential between two fragments.
Assuming that a compound nucleus separates into a certain pair of fission fragments,(ACN,ZCN)→(A1,Z1)+(A2,Z2),with a mass numberACN=A1+A2and charge numberZCN=Z1+Z2in the fission process,we define the driving potential of the fissioning system as,
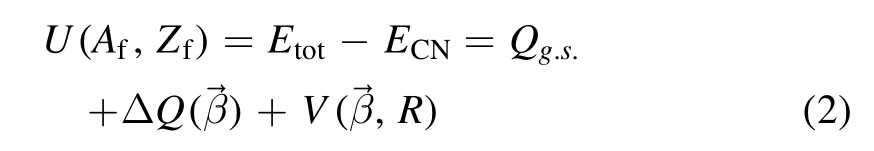
with mass number Afand charge number Zffor one fragment.The driving potential describes the potential energy of the fissioning system around scission configuration.ECNand Qg.s.denote the energy of the compound nucleus at its ground stat e and the Q value of the reaction system,respectively.denotes the deformations of fission fragments around scission configuration.In this work,the static deformations for each fission fragment,i.e.,the deformations for nuclei at their ground states,are determined by Weizsäcker–Skyrme(WS) mass model [26].Simultaneously,the dynamical deformations βDof fragments are also considered.ΔQ=[E1(βD)-E1g.s.]+[E2(βD)-E2g.s.]denotes the change of the potential energies for the fission fragments with respect to the individual energies at their ground states due to the dynamical deformations.
For a description of the elongated tip–tip structure of a fissioning system around the scission point,nuclear prolate shapes and the octupole deformations should play a dominant role.In this work,we take the absolute value |β2| for nuclei with oblate deformations and set the values of dynamical octupole deformationβD3for a pair of fission fragments to be the same but in reverse for simplicity.By varying the value ofβD3for a certain pair of fission fragments at the position of the potential barrier where the two fragments are slightly separated and searching for the minimal value of the driving potential U,one can obtain the optimal value forβD3which is about 0.1–0.2(one can find the similar result from figure 10 in[27]).For fragments with spherical shapes at their ground states,the dynamical quadrupole deformationsβD2are also considered,and the values ofβD2are obtained like those forβD3.
From equation (2),one can see that in addition to the interaction potential,both the properties of fragments at their ground state and the dynamic deformations around scission configuration influence the potential energy surface of a fissioning system.The microscopic shell effect and pairing effect are effectively involved in the calculations of Qg.s.and the residual part ΔQ.The values of Qg.s.are mainly taken from the measured masses with high accuracy in AME2016[28,29].For the masses of unmeasured nuclei and the value of ΔQ,we use the predictions of the WS mass models[26,30].We would like to emphasize that the driving potential U for a certain fissioning system can be unambiguously obtained from the Skyrme energy-density functional and the WS mass models,without introducing any new model parameters.
3.Results and discussions
Considering that the mass and charge number of fission fragments are distributed at a wide range,the driving potential U(Af,Zf) of a certain compound nucleus separating into different pairs of fission fragments is investigated.For example,the driving potential for fission of236U with about five hundred different pairs of fission fragments is calculated and the results are shown in figure 1(a).Figure 1(b)shows the data for the charge distribution of primary fission fragments in thermal-neutron-induced fission of235U(nth,f)[31].One sees from the driving potential that there exists two deep valleys located around (Af=140,Zf=54) and (Af=96,Zf=38)which exactly respond to the peaks of the mass and charge distributions of fission fragments.It indicates that the yields of fission fragments of236U at low excitation energies are closely related to the corresponding driving potential.
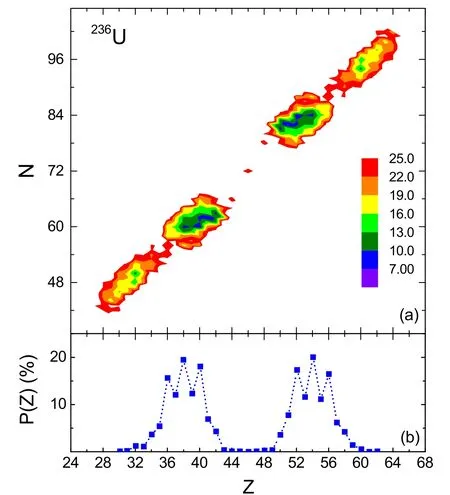
Figure 1.(a) Calculated driving potential (in MeV) for fission of 236U.(b) Charge yields of fission fragments for 235U(nth,f) [31].
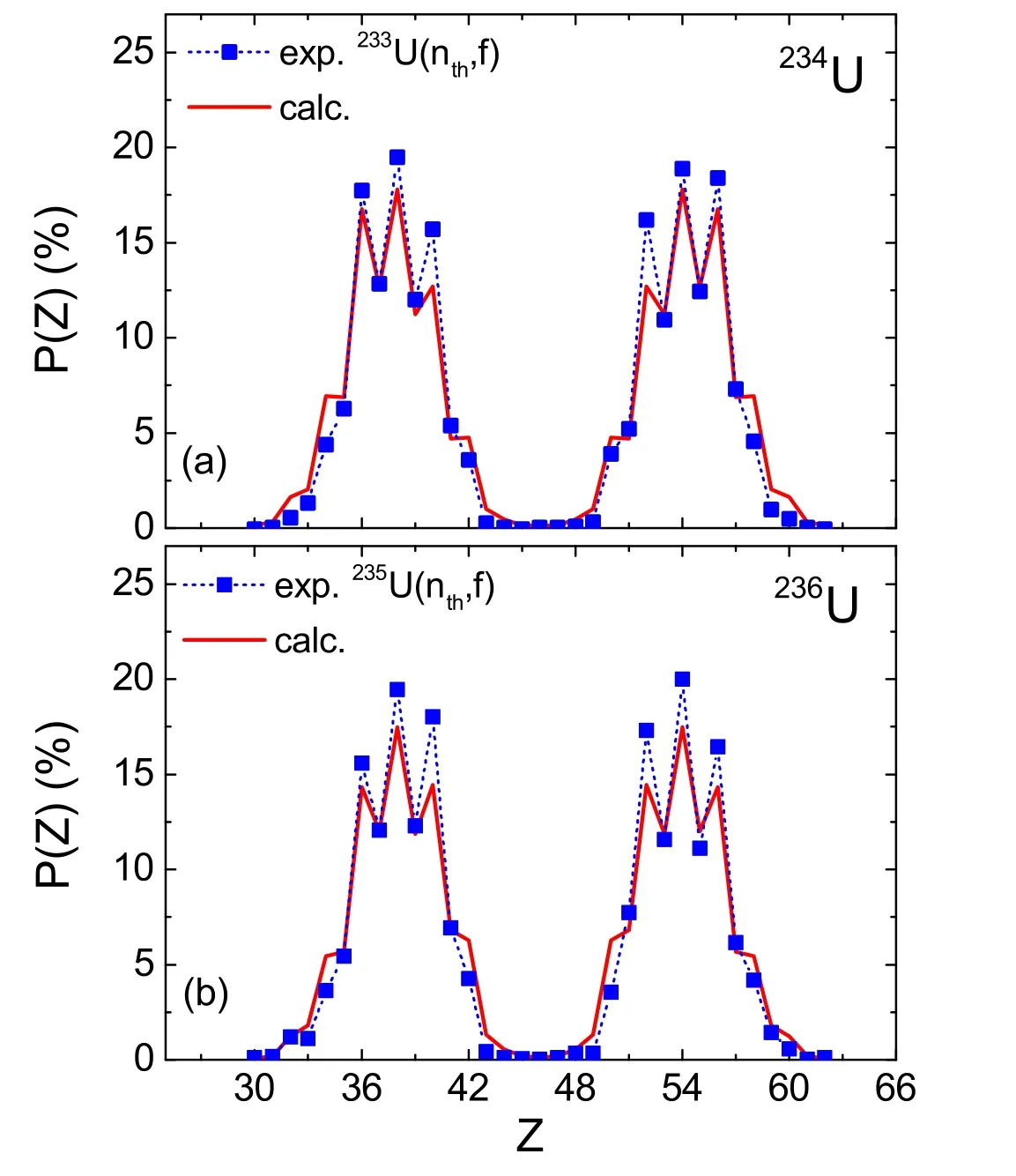
Figure 2.Calculated and measured charge yields for fission of 234U and 236U.The squares denote the experimental data for thermalneutron-induced fission of 233U(nth,f) and 235U(nth,f)[31].The red curves denote the calculated results with equation (3).
Based on the calculated driving potential,the corresponding fragment charge distributions for a fissioning system are further predicted.In this work,the yields of fission fragments for a fissioning system is expressed as,

K is a model parameter,which relates to the temperature of the system around the scission point.Here,we empirically setK=0.38ACN-83.35(in MeV) for describing the fragment yields in the fsision of actinides at low excitation energies.The corresponding coeffciients in K are determined by the measured fsision-fragment charge distributions for a series of actinides.The normalization factorC(Af)=P(Af)/∑Zfexp[-U/K]can be uniquely determined by a given fragment mass distribution P(Af).In the present calculations,we use the measured fragment mass distribution for the determination of the normalization factor C.If P(Af) is not available,one could use the empirical fission potential[32]for calculating the mass distributions.With the driving potential and mass distribution,the charge distributions of the primary fsision fragmentsP(Zf)=∑AfY(Af,Zf)can be directly calculated with equation(3).Here,we wouldlike to emphasize that equation (3) is only applicable for describing the thermal-induced and spontaneous fission of actinides.If one would like to extend this model to describe the distributions of fission fragments and yields at high excitation energies,the temperature dependence for the driving potential U,the normalization factor C and the model parameter K should be considered.
Figure 2 shows the calculated charge distribution of primary fragments for fission of234U and236U.The experimental data for thermal-neutron-induced fission of233U(nth,f)and235U(nth,f),especially the odd–even staggering can be well reproduced.From equation (2),one can see that nuclear deformations influence the value of ΔQ and the interaction potential V in the calculations of the driving potential.To see the influence of nuclear deformations on the charge distributions,we compare the calculated results with nuclear ground state deformations from the WS model[26]and those from the finite range droplet model(FRDM)[33].In figure 3,we show the calculated charge distribution of primary fragments for thermal-neutron-induced fission of234U,236U,240Pu and spontaneous fission of252Cf.The red curves and the green circles denote the calculated results from the WS model and the FRDM model,respectively.Here,the data for the mass distributions of233U(nth,f) [34],235U(nth,f) [35],239Pu(nth,f) [36]and spontaneous fission of252Cf [37]are adopted for the determination of the normalization factors C,respectively.One sees that with nuclear deformations from both mass models,the fragment charge distributions for fission of234U,236U,240Pu and252Cf can be reasonably well reproduced.The difference due to the predicted nuclear deformations from the two models can also be obviously observed for light fragments with Z=42.The yields for fragments with Z=42 and the corresponding partners based on the deformations from the FRDM model is much higher than those from the WS model,especially for the fission of U and Pu.According to the driving potential shown in figure 1,the most probable neutron number is around N=60 for fragments with Z=42.We note that the predicted quadrupole deformation (β2=0.329)from the FRDM model is much larger than that from the WS model (β2=0.210) for102Mo.The quadrupole deformation of nuclei can significantly affect the interaction potentialV(β→,R)between fragments.With larger quadrupole deformation,one obtains a lower potential barrier and thus lower driving potential which results in higher yields in the charge distributions.
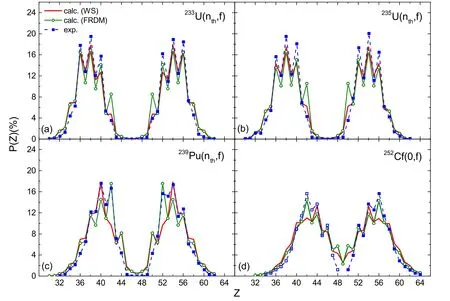
Figure 3.Calculated and measured charge yields for thermal-neutron-induced fission of 234U,236U,240Pu and spontaneous fission of 252Cf.The squares denote the experimental data taken from[31,38].The red curves and the green circles denote the calculated results with nuclear ground state deformations from the WS model and the FRDM model,respectively.The open squares in (d) denote the charge distributions obtained from the mirror of the measured heavy fragments.
In [5],Randrup and Möller calculated the charge yields for fission of234,236U and240Pu based on Brownian motion on the five-dimensional potential-energy surfaces (5D-PES).We note that the odd–even staggering in the experimental data is not reproduced at all with their approach.To understand the physics behind the odd–even staggering in charge distribution,we explore the influence of the pairing effect on the charge distribution.In the calculations of Qg.s.in equation (2),we remove the contribution of the pairing term which is expressed as apairA-1/3δnpin the WS model [26],with

The corresponding calculation results for the fission of236U are shown in figure 4.One sees that the odd–even staggering disappears,which clearly indicates that the pairing effect in fragments at their ground state plays a key role in the odd–even staggering in the charge distribution.
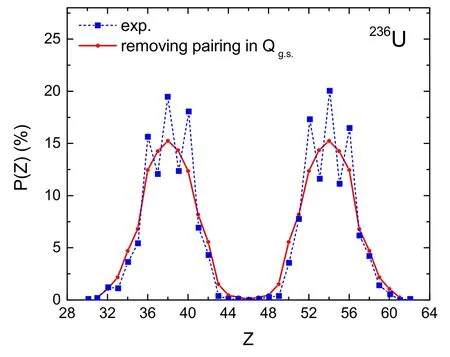
Figure 4.The same as figure 2(b) but removing the pairing term in the calculations of Qg.s..

Figure 5.Comparison of the model parameter K and the change of Q value from asymmetric fission to the symmetric one.
To understand the physics behind the model parameter K in equation(3),we investigate the change of the Q values for eight actinides,230Th,234,236U,240,242Pu,246Cm and250,252Cf,from asymmetric fission to the corresponding symmetric ones.Considering that one peak of the fission-fragment mass distribution is usually located at about Af=140 and the corresponding peak of charge distribution is about Zf=54 for these actinides at low excitation energies,we calculate the corresponding ground-state Q value,defined as,with one fragment being140Xe.In figure 5,we show the difference between the Q value for the asymmetric fission and that for the symmetric oneQgs.ys.m.One can see that the increasing trend of-with mass number is very close to that of K.-in figure 5,which relates to the degree-of-One could note that there exists a shift of 4.4 MeV to freedoms,e.g.the diffuseness and deformations of fission fragments,adopted in the calculations of the driving potential.We also note that if takingK=-+4.4in the calculations,the obtained fragment charge distributions are comparable to those withK=0.38ACN-83.35.It seems that the value of K may have a relationship with the difference in the Q value.
4.Summary
In summary,the description of the fission-fragment charge distribution of actinides can be significantly improved with the driving potential of the fissioning system which creates a bridge between the mass distribution and the charge distribution.Since a number of fission-fragment charge yields have not yet been measured while the corresponding mass distributions are available,the predictions for charge distributions based on the driving potential are quite useful and interesting.Considering the properties of primary fission fragments at their ground states,the potential energies of systems around scission configuration can be unambiguously and quickly obtained from the Skyrme energy-density functional and the WS mass models.The odd–even effect in the charge distributions which links nucleon transfer through the neck in the regime of strong pairing correlations is much better reproduced,compared with the traditional potential energy-surface approach in which the determination of the model parameters,especially the strength of pairing force,becomes difficult for the extremely deformed shapes.There are two advantages to the proposed approach: (1) The CPU time is significantly shortened because only thousands(in the calculations of ΔQ) rather than millions of wave equations need to be solved to obtain the potential energies of the system in the calculation of the fission-fragment yields.(2)The microscopic shell and pairing effects are more accurately taken into account via the measured Q value and the residual term ΔQ,which are calculated by using the WS mass models with high accuracy for describing the known masses[39].We find that the structure effect of fragments at their ground state,such as the deformations and the odd–even staggering,play a crucial role in the fission of actinides around scission at low excitation energies.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Nos U1867212,11 875 323,12 147 211) and Guangxi Natural Science Foundation (No.2017GXNSFGA198001).
 Communications in Theoretical Physics2022年9期
Communications in Theoretical Physics2022年9期
- Communications in Theoretical Physics的其它文章
- Preface
- Phase behaviors of ionic liquids attributed to the dual ionic and organic nature
- Chaotic shadows of black holes: a short review
- QCD at finite temperature and density within the fRG approach: an overview
- The Gamow shell model with realistic interactions: a theoretical framework for ab initio nuclear structure at drip-lines
- Effects of the tensor force on low-energy heavy-ion fusion reactions: a mini review
