Effects of the tensor force on low-energy heavy-ion fusion reactions: a mini review

Xiang-Xiang Sun (孙向向)and Lu Guo (璐郭),∗

1 School of Nuclear Science and Technology,University of Chinese Academy of Sciences,Beijing 100049,China

2 CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

Abstract In recent several years,the tensor force,one of the most important components of the nucleon—nucleon force,has been implemented in time-dependent density functional theories and it has been found to influence many aspects of low-energy heavy-ion reactions,such as dissipation dynamics,sub-barrier fusions,and low-lying vibration states of colliding partners.Especially,the effects of tensor force on fusion reactions have been investigated from the internuclear potential to fusion crosssections systematically.In this work,we present a mini review on the recent progress on this topic.Considering the recent progress of low-energy reaction theories,we will also mention more possible effects of the tensor force on reaction dynamics.

Keywords: low-energy heavy-ion collision,time-dependent density functional theory,ion—ion potential,fusion cross sections,tensor force

1.Introduction

The tensor force is one of the important components of the nucleon—nucleon forces and is of great interest in nuclear physics.The most typical example to show the significance of the tensor force is that it provides a strong central attraction in the isospin zero channel which is responsible for the deuteron binding.With the development of radioactive-ion-beam facilities,many exotic phenomena,such as the existence of nuclear halos and skins [1,2],clustering effects [3],shape coexistence [4],the changes of shell closures [5],the pygmy resonances in electric dipole transitions [6]have been observed in the region far away from the β-stability valley.The studies of these exotic nuclear structures are at the forefront of nuclear research nowadays and many experimental and theoretical efforts have been made in recent years[4,7—16].The tensor force plays a particularly important role in the shell evolution in exotic nuclei[17].This has motivated many studies of the effect of the tensor force on the shell structure of exotic nuclei,spin—orbital splitting,single-particle states,and deformations by using nuclear density functional theories or shell models.Encouraging progress has been made,see [16,18]for recent reviews.More interesting and complicated topics are to explore the relationship between nuclear structure and reaction mechanism [19,20],especially via low-energy heavy-ion reactions of exotic nuclei,such as weakly bound or halo nuclei and nuclei with a large neutron excess,and to understand the role of the tensor force in these processes.

The microscopic description for the low-energy heavyion collisions should originate from the underlying interaction,the interaction between the nucleons.The understanding of reaction dynamics is still one of the most challenging topics in nuclear physics nowadays.The study of the heavyion reactions with microscopic models and the comparison between results from model calculations and experimental data[21,22]are helpful to test some properties of the nuclear force and revealing the influence of nuclear structures on reactions.At present,the microscopic description of the reaction process can be achieved by using the time-dependent density functional theories,in which the adopted effective interactions between nucleons are constructed from basic symmetries of the nuclear force and the involved parameters are determined by fitting to characteristic experimental data of finite nuclei and nuclear matter.These effective interactions include non-relativistic and relativistic ones and the timedependent calculations based on both [23—27]have been achieved.It should be mentioned that in the time-dependent covariant density functional theory developed in recent years[23—25,28],the tensor force is not included.Therefore in this work,we focus on the time-dependent calculations by using the non-relativistic effective interactions,i.e.the Skyrme force,to show the effect of tensor force on low-energy heavyion reactions.

In heavy-ion reactions,various couplings between the relative motion and the excitation in the internal degrees of freedom of colliding systems should be considered in principle and thus make the description of the reaction mechanisms more complicated.The internal excitations of reactants include collective ones and non-collective ones,such as low-lying vibrations [29—31],nucleon(s) transfer [32—34],rotations [35],and high-lying giant resonances [36].The coupling between the relation motion and internal excitation can be usually treated by using the coupled-channels approaches [37]and it has been shown that the reaction dynamics and,subsequently,the outcome of the reaction can be affected by these couplings.

The effects of tensor force on these couplings in heavyion reaction dynamics are still open questions.It has been mentioned that the low-energy heavy-ion reactions are affected by different couplings between relative motion and the excitation of collision partners.Among these couplings,those from low-lying collective motion and nucleons transfer,which strongly influence near-barrier fusion,are very sensitive to the underlying shell structure,which can be affected by the tensor force.Another effect of the tensor force is that it modifies the dynamic dissipation in heavy-ion collisions[38].The latter has been the subject of theoretical studies at energies well above the Coulomb barrier[38—40].In recent years,several heavy-ion fusion reactions between medium or heavy nuclei have been studied by the time-dependent density functional theory considering the tensor force,and how the tensor force influences the fusion cross section has been investigated[39,41—45].Therefore,in this work,we focus on the recent progress in the study of fusion reactions with considering the contributions from the tensor force.

To study fusion reactions at both above and below-barrier energies,the starting point of most theoretical approaches is the nucleus—nucleus potential.There are mainly two kinds of models to determine the nucleus—nucleus potential: phenomenological potentials [46—56]and (semi)microscopic ones [22,57—68].The phenomenological models have been widely applied to study many aspects of reactions,but their predictive power is limited due to several adjustable parameters,such as the Bass model [46],the proximity potential [47,69],the doublefolding potential [48],and driven potential from dinuclear system model[49].The fusion process is particularly complex and the cross section is affected by many effects.The predictions from a microscopic model in the nucleonic degrees of freedom are more reliable and particularly a microscopic description can be connected with the underlying nuclear shell structure and dynamic effects of the reaction system rely on the adopted density functionals.In such a way,it is also possible to check and analyze how the underlying effective interaction and its components,such as tensor force,affect the dynamic process and fusion cross sections.After obtaining the internuclear potential based on microscopic effective interactions with or without tensor components,one can calculate the fusion cross sections by using the standard coupled-channels method[70].In this way,the effect of tensor force on fusion reactions can be analyzed.To this end,this review is organized as follows.We introduce the theoretical framework to determine the internuclear potential with the Skyrme effective interaction with or without tensor force and fusion cross sections in section 2.Sections 3 and 4 present the influences of the tensor force on the internuclear potentials and fusion cross sections,respectively.The summary and perspective are shown in section 5.

2.Theoretical framework

In this section,we firstly show the tensor component in the Skyrme effective interactions.Then a brief introduction of the time-dependent Hartree—Fock (TDHF) is given.Three approaches to obtaining the internuclear potentials and the method used to calculate the fusion cross section are also presented.

2.1.Tensor force in Skyrme effective interaction

Although the TDHF approach has been widely applied to low-energy heavy-ion reactions,various assumptions and approximations that might affect the TDHF results and lead to the incorrect reproduction of measurements have been employed in the past.To remedy these problems considerable theoretical and computational efforts have been taken to improve numerical treatments and density functionals.An early discrepancy between TDHF predictions and measurements[71,72]had been solved by including the contributions from spin—orbit interactions,which turned out to play an important role in reaction dynamics [73,74].In recent years with the developments of high-performance computing equipment,TDHF calculations on a three-dimensional Cartesian grid without any symmetry restrictions have been achieved.Additionally,the time-odd interactions,which have non-negligible contributions to heavy-ion collisions,have also been included [26].Recently the tensor force is also implemented in the state-of-art TDHF calculations and it can also affect the reaction dynamics [39,41].

In this paper,we focus on the effects of tensor force on heavy-ion reactions.The tensor terms in the Skyrme effective interaction [75]read

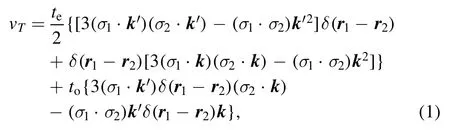
where teand toare the strengths of triplet-even and triplet-odd tensor interactions,respectively.

In TDHF theory,the energy of a nucleus is a functional of various densities and reads

where ρ,τ,j,s,T,F,and J are the number density,kinetic density,current density,spin density,spin-kinetic density,tensor-kinetic density,and spin-current pseudotensor density,respectively [39].Thus the full version of Skyrme energy density functional can be expressed as

where H0is the simplified functional used in the TDHF code Sky3D[27]and most TDHF calculations.Those terms with the coupling constants A come from the central and spin—orbit interactions and those with B from the tensor force.The details of A and B can be found in[76,77].It should be mentioned that up to now all the time-even and time-odd terms in equation(3)have been included in the static Hartree—Fock(HF),TDHF,and density-constrained (DC) TDHF calculations.

Two ways have been applied to determine the parameterization of the tensor components in Skyrme density functionals.The first one is to include the tensor force perturbatively to the existing density functionals,for instance,the effective interaction SLy5 [78]plus tensor force,labeled as SLy5t [79].Therefore,by making the comparison between calculations with SLy5 and those with SLy5t,one can know the changes caused by the tensor force itself.By readjusting the full set of Skyrme parameters self-consistently,the strength of the tensor force can also be determined.This strategy has been used in[76]and led to dozens of parameter sets of tensor interactions,denoted as TIJ.Due to its fitting strategy,the contributions from the tensor force and the rearrangement of all other terms are physically entangled.

2.2.TDHF approach

The action corresponding to a given Hamiltonian can be constructed as

where Φ(r,t) is the time-dependent wave function for the many-body system with N nucleons.Under the mean-field approximation,the many-body wave function Φ(r,t) is the single time-dependent Slater determinant constructed by the single-particle wave functions φλ(r,t) and reads

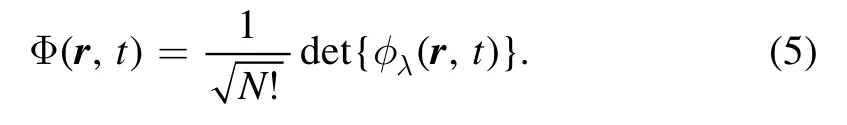
With the variation principle,i.e.taking the variation of the action with respect to the single-particle states,the equations of motion of the N nucleons are

with the single-particle Hamiltonian h.These nonlinear TDHF equations have been solved accurately on threedimensional coordinate space without any symmetry restrictions [26,27].The TDHF approach can provide a microscopic description of nuclear dynamics,as seen in recent applications to fusion reactions [67,68,80—90],quasifission process [91—95],transfer reactions [32—34,96—100],fission[101—109],and deep inelastic collisions [38—40,73,74,110—114].More applications of the TDHF can be found in recent reviews [115—119].

2.3.Microscopic internuclear potentials and fusion cross sections

The TDHF simulation,based on the mean-field approximation,provides the most probable trajectory of the collision system and the quantum fluctuation is not included.The quantum tunneling of the many-body wave function cannot be treated with the TDHF approach.As a consequence,the TDHF approach cannot be directly applied to study subbarrier fusion reactions.It should be noted that an imaginarytime mean-field method might be the answer to this problem[120].The fusion cross section can be estimated by the quantum sharp-cutoff formula [26,44,121,122]based on a mass of TDHF simulations with different incident parameters or angular momenta,but which may underestimate the cross sections especially for sub-barrier collisions.Currently,all approaches to studying sub-barrier fusions assume that there is an internuclear potential that depends on the internuclear distance and the fusion reaction is usually treated as a quantum tunneling through this potential in the center-ofmass frame.The internuclear potential can also be calculated microscopically with the TDHF approach by applying frozen Hartree—Fock (FHF) [83,123],density-constrained FHF(DCFHF)[68,124],DC-TDHF[62],or dissipative-dynamics TDHF [66]approach.The obtained potential can be used to calculate penetration probabilities with the incoming wave boundary condition (IWBC) method [70].In this section,we will introduce the FHF,DCFHF,and DC-TDHF methods and how to calculate the cross section with those internuclear potentials.

Based on the TDHF dynamic evolution of the collision system,the internuclear potential can be extracted by using the density constraint technique.As a consequence,the obtained potential contains all dynamic effects,such as neck formation,dynamic deformation effects,and particle transfer.In this approach,at a certain moment during the TDHF evolution,the instantaneous TDHF density is used to perform a static HF energy minimization

by constraining the proton and neutron densities to be the same as the instantaneous TDHF densities.Since the total density is constrained to be unchanged,all mass moments are simultaneously constrained.λ is the Lagrange parameter at each point of space.|ΨDC〉 is the many-body wave function under the density constraint.The energy corresponding to the|ΨDC〉,i.e.the DC energy,reads

This energy still includes the binding energies of two colliding nuclei,which should be subtracted.Then the internuclear potential is given by

where EPand ETare the binding energies of the projectile(P)and target(T),respectively.It should be noted that the density constraint procedure does not influence the TDHF evolution and does not contain any free parameters or normalization.In this approach,all the single-particle levels are allowed to reorganize during minimizing the total energy,thus the Pauli exclusion principle is included dynamically.

Compared with the internuclear potentials from DCTDHF,those from the DCFHF method do not include any dynamic factors and the contribution from the Pauli exclusion principle is still included.The Pauli exclusion principle is included by allowing the single-particle states to reorganize to attain minimum energy in the static HF calculations with the density constraint and to be properly antisymmetrized,as the many-body state is a Slater determinant of all the occupied single-particle wave functions.The HF calculations are preformed by constraining the total proton p and neutron n densities to be the same as those at the ground state

where ρPand ρTare the densities of the projectile and target in their ground states.This variation procedure results in a unique Slater determinant Φ(R).Similar to the case of DCTDHF,the internuclear potential from DCFHF is given by

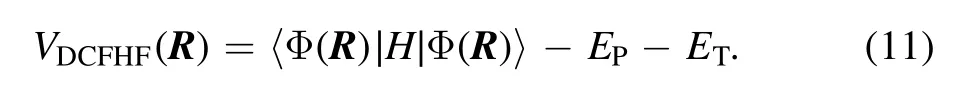
From above,the DC-TDHF has been introduced to compute the nucleus—nucleus potential in a dynamical microscopic way.All of the dynamical effects included in TDHF and the Pauli exclusion principle are then directly incorporated.For the one from DCFHF,the dynamic effects are not included while the Pauli exclusion principle is still kept.There is also a potential which includes neither dynamical effects nor the contributions of the Pauli exclusion principle.This nucleus—nucleus potential is defined as the potential between the nuclei in their ground states.This is achieved with the FHF technique [31],assuming that the densities of the target and projectile are unchanged and equal to their ground state densities.The potential can then be expressed as

When the internuclear distance is large,i.e.the overlap between the densities of the projectile and target is small,the Pauli principle almost has no influence on the internuclear potential.However,when two nuclei are close to each other and the density overlaps are large,the Pauli principle is expected to play an important role.Therefore the FHF approximation cannot properly describe the inner part of the potential [68].

After obtaining internuclear potentials,the fusion cross section can be calculated.It has been mentioned that including the couplings between the collective excitation of the target and projectile plays a significant role to describe the fusion excitation function.As mentioned above,the internuclear potentials from FHF and DCFHF do not include any dynamic information and can be directly applied to the coupled-channels approach [70]to calculate the fusion cross sections[68].It should be noted that the combination of FHF method with the coupled-channels calculation can provide a reasonable description of fusions at near-barrier regions [31],but cannot be used to study fusion reactions well below the barrier or in systems with large ZPZT[124,125]because the Pauli repulsion is not included.When calculating the fusion cross sections by using the potentials from DCFHF together with the coupled-channels method,it has been shown that calculated results are more consistent with the measurements than those from FHF potential [68],especially in sub-barrier region.

The DC-TDHF approach provides a microscopic way to obtain internuclear potentials,which already contain all the dynamic factors and is connected with the coordinatedependent mass M(R).Therefore,the fusion cross sections can be directly calculated by solving the one dimensional Schrödinger equation with the potential extracted from DCTDHF.The procedure to obtain transmission probabilities Tl(Ec.m.) (and thus cross sections) from an arbitrary onedimensional potential V(R) can be calculated by solving the Schrödinger equation

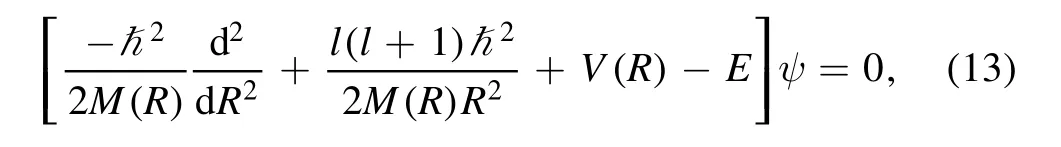
where l is the angular momentum of each partial wave.Generally,the IWBCs method is used to calculate Tl(Ec.m.)with the assumption that fusion occurs once the minimum of V(R) is reached.After obtaining Tl(Ec.m.),fusion cross sections are given by

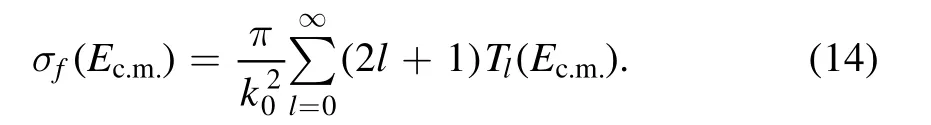
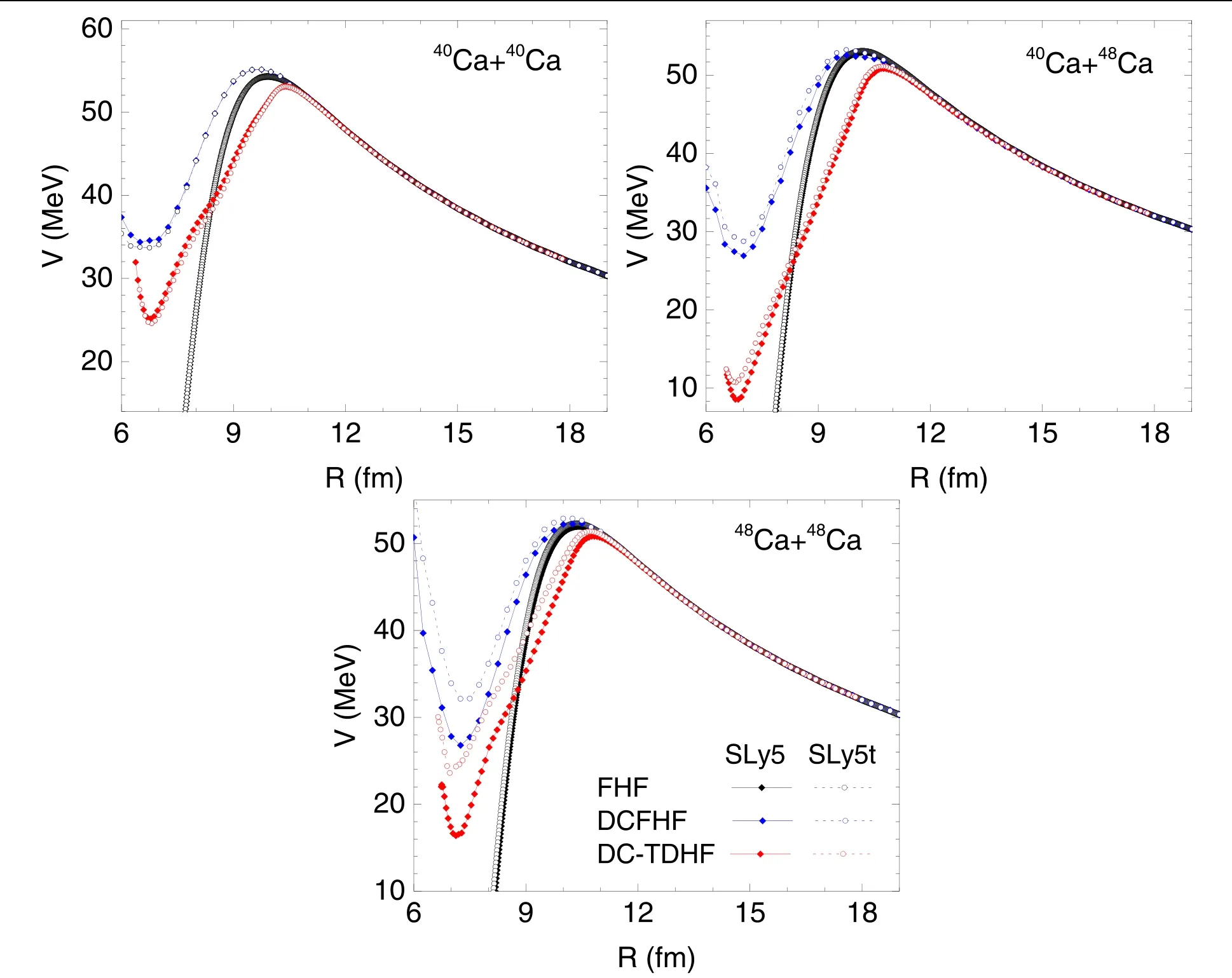
Figure 1.Internuclear potentials for 40Ca+40Ca,40Ca+48Ca,and 48Ca+48Ca by using FHF,DCFHF,and DC-TDHF methods with the effective interactions SLy5 and SLy5t.The results from FHF and DC-TDHF calculations are taken from [42].

Since DC-TDHF potentials are the results of the TDHF evolution,the coordinate-dependent mass M(R) can be calculated with the energy conversation condition [81,126]

This coordinate-dependent mass mainly influences the inner part of the potential,leading to a broader barrier width thus further suppressing the fusion cross sections at the sub-barrier region.The potentials from DC-TDHF are dependent on the incident energy Ec.m.and the energy-dependence behavior is also affected by the coordinate-dependent mass [86].Instead of solving the Schrödinger equation using the coordinatedependent mass M(R),one can also calculate the fusion cross sections by using a transformed potential [126,127]and the scale transformation reads

After this transformation,the coordinate-dependence of M(R)is replaced by the reduced mass μ in equation (13) and the Schrödinger equation is solved by using the modified Numerov method with the transformed potential.The details have been introduced in the coupled-channels code CCFULL[70].With the internuclear potentials from DC-TDHF approach,the fusion cross sections at below and above-barrier energies of many systems are studied and good agreements between calculations and experimental data are achieved[41—43,45,62,67,81,82,84—86,94,126,128—133].

3.Effects of tensor force on internuclear potentials

The internuclear potentials from FHF,DCFHF,and DCTDHF methods only rely on the adopted effective interactions and there are no additionally readjusted parameters.The influence of tensor force can be examined by making a comparison between the calculated potentials with the tensor force and those without the tensor force.In figure 1,we show the internuclear potentials between40Ca+40Ca,40Ca+48Ca,and48Ca+48Ca by using FHF,DCFHF,and DC-TDHF methods with the effective interactions SLy5 and SLy5t.Before discussing the effects of the tensor force,we make a comparison among these three types of potential.It is found that for a reaction system with given effective interaction,the internuclear potentials from DC-FHF have the highest capture barriers while barriers corresponding to the DC-TDHF method are the lowest.Due to the absence of the Pauli repulsion,the internuclear potentials from the FHF method do not have a strong repulsion core.The inclusion of the Pauli repulsion increases the height of the Coulomb barrier,leads to the appearance of the potential pocket in the inner part,and changes the shape of the barrier.When including dynamic effects,i.e.for the potentials from DC-TDHF calculations,both the minimum potential pocket and the capture barriers become lower because of the inclusion of dynamic factors.

Figure 2.Internuclear potentials for 48Ca+48Ca by using DC-TDHF(left panel)and DCFHF(right panel)with effective interactions SLy5,SLy5t,T22,T24,T44,and T62.

In[42],different combinations of projectile and target with proton and neutron numbers being the magic numbers 8,20,28,50,and 82 have been chosen to investigate how the tensor force affects the nucleus—nucleus potential from FHF and DCTDHF calculations.Among these magic numbers,the spinsaturated shells are 8 and 20.It is found that for light systems or reactants with spin-saturated shells the tensor force slightly affects the barrier height and inner part of the barrier by a fraction of a MeV and for medium and heavy spin-unsaturated reactions the effect is much more obvious,with changes from a fraction of a MeV to almost 2 MeV.Figure 1 shows the comparison of the internuclear potentials obtained from the three methods mentioned-above with density functionals SLy5 and SLy5t.It is found that for40Ca+40Ca,the tensor almost has no influence on internuclear potential because the shell closure at N(Z)=20 is spin-saturated.For40Ca+48Ca and48Ca+48Ca,it is found that the tensor force increases the capture barriers and minimum of potential pockets.Additionally,for the internuclear potentials for40,48Ca+78Ni with SIII(T) [134,135]and SLy5(t) shown in [45],it is found that the tensor can influence the shape of the barrier.

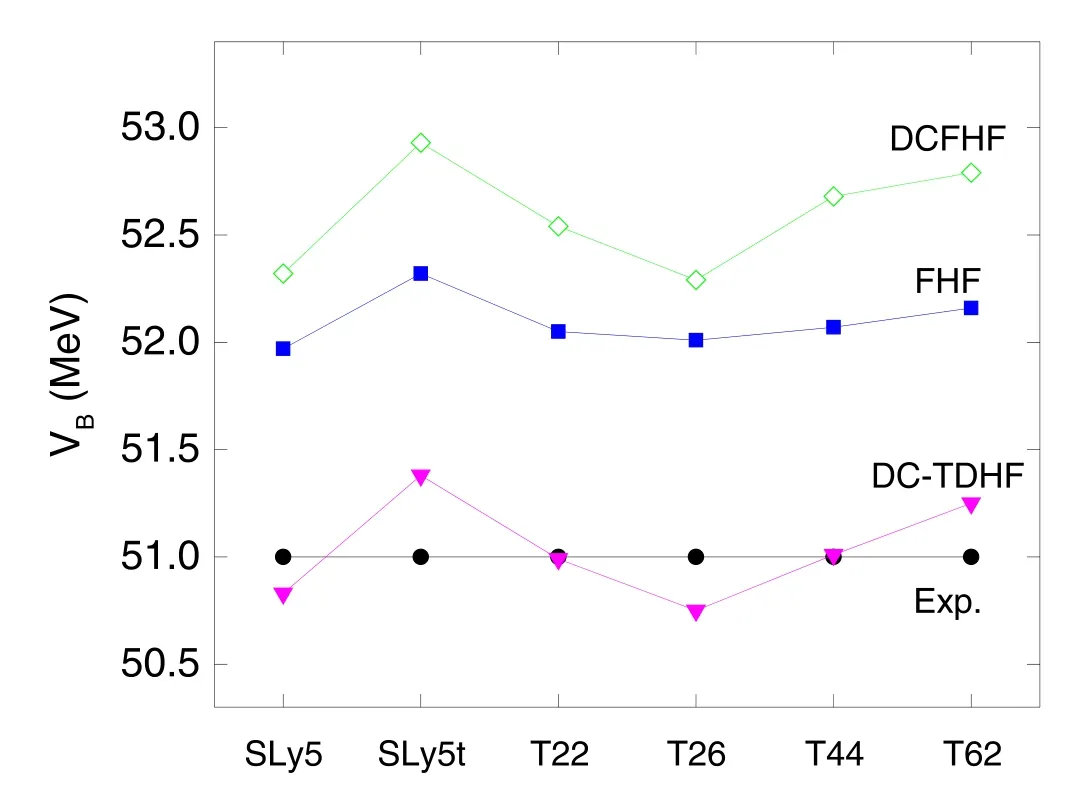
Figure 3.The heights of barriers for 48Ca+48Ca calculated by using FHF,DCFHF,and DC-TDHF with six Skyrme forces as well as the experimental value taken from [136].The capture barriers for FHF and DC-TDHF calculations are extracted from the results given in [42].

As mentioned before,the tensor components in SLy5t force are added perturbatively.Therefore,it is necessary to make a comparison among the results of various forces,for which the coupling constants of tensor force are obtained by readjusting the full set of Skyrme parameters self-consistently.Taking the system48Ca+48Ca as an example,we show the nucleus—nucleus potential with the six forces SLy5,SLy5t,T22,T26,T44,and T62 in figure 2 by using the DCFHF and DC-TDHF methods.The height of barriers of these potentials is shown in figure 3 and the experimental capture barrier taken from [136]is also given.Generally speaking,the barriers of potentials from DCFHF are higher and wider than those from the DC-TDHF method.From figure 3,it is clear that the barriers from DC-TDHF calculations are well consistent with the experiment and those of FHF and DCFHF are higher than in the experiments.This is due to the potentials from DC-TDHF containing dynamic effects,such as dynamic deformations and neutron transfers.It has been shown [42]that different parameterizations of tensor force have different influences on the low-lying excitations and neutron (proton) transfer such that the effects on the barrier heights differ by effective interaction.In[42],the comparison among the internuclear potentials from DC-TDHF and related discussions have been made.The comparison between T22 and T44 indicates that the isoscalar channel has a negligible effect in this reaction.By comparing the results with T26,T44,and T62,one can see that the potential increases as the isovector tensor coupling decreases.The potentials with T62(T26)have similar potentials as SLy5t(SLy5),even though their tensor coupling constants are quite different because the rearrangement of the mean-field for T62(T26) might cancel part of the tensor force in SLy5t (SLy5).

4.Effects of tensor force on fusion cross sections

In section 3,we have shown that the tensor force not only influences the barrier height but also affects the shape of the barrier.Therefore,the tensor force should,in principle,affect the fusion cross sections,particularly for sub-barrier energies.To calculate the fusion cross section,as for the potentials from FHF and DCFHF,one should fit them to the Woods—Saxon type potential and then uses the CCFULL [70]to calculate the fusion cross sections with considering the coupling from low-lying excited states [68].As for the potential from DC-TDHF calculation,one can directly calculate the penetration probabilities under the transformed potentials such that the fusion cross sections can be obtained [see equation (14)].

The tensor force almost has no influence on the internuclear potentials of the system in which both the projectile and target have spin-saturated neutron and proton shells,e.g.40Ca+40Ca.In [43],the effect of tensor on the fusion cross sections obtained by using the potential from DC-TDHF has been discussed and it is shown that for those systems with spin-saturated shells,the tensor force has no influence on fusion cross sections.For the systems with spin-unsaturated proton (neutron) shells,the tensor force has non-negligible effects,such as40,48Ca+48Ca [43]and40,48Ca+78Ni [45].Especially for the sub-barrier region,the inclusion of the tensor force improves the description of fusion cross sections for48Ca+48Ca collision.In [43],a systematic comparison between the fusion cross sections considering the tensor force and those without the tensor force has been made.Up to now,the effects of tensor force on fusion cross sections by using the potential from DCFHF have not been clarified.Therefore,we use the internuclear potentials from DCFHF to investigate this problem by taking48Ca+48Ca as an example.

Figure 4.Fusion cross sections obtained by using the potentials from DCFHF calculations and experimental data taken from [136]for 48Ca+48Ca.The top panel shows the results calculated with the effective interactions SLy5 and SLy5t.Those for effective interactions T22,T24,T44,and T62 are shown in the bottom panel.

The calculated capture cross sections with the potentials from DC-TDHF have been shown in [43]and the results reproduce the data well.In figure 4,we show the fusion cross sections of48Ca+48Ca calculated by using the code CCFULL with the internuclear potentials from the DCFHF approach and considering the coupling from low-lying vibration states 21+and31-of48Ca.It is found that the calculations reproduce the recent measurements[136]well.The comparison between the results from SLy5 and SLy5t indicates that by including the tensor force perturbatively,the tensor force suppresses the fusion cross sections in the below-barrier region.By comparing the results from DC-TDHF [43]and DCFHF,one can find that the suppression of the cross section at a sub-barrier region in DC-TDHF calculations is more obvious than that of DCFHF.This is due to the heights of barriers corresponding to the DCFHF method being higher than those of DC-TDHF.After considering the tensor force,the description of the subbarrier fusion cross section is slightly improved.The results from TIJ forces differ from each other,suggesting the competition between isoscalar and isovector channels plays a role in reaction dynamics.For TIJ forces,the conclusions obtained from DC-TDHF calculations also hold in DCFHF calculations.It should be noted that here we directly use the experimental information of21+and31-given in [136]and it has been shown in [41]that the tensor force also influences the low-lying vibration properties of exotic nuclei such that the influence of tensor force might be more complex.Selfconsistent and systematic studies on the influence of tensor force on low-lying spectra,internuclear potentials,and fusion cross section are necessary.

5.Summary and perspective

The effects of the tensor force on nuclear structures and nuclear reactions are of great interest nowadays.Accurate description of the fusion cross sections especially at the subbarrier energies for reactions involving exotic nuclei are very important topics in nuclear reactions.In this contribution,we briefly review recent progress on the effects of tensor force on low-energy heavy-ion fusion reactions.We calculate the internuclear potentials for40,48Ca+40,48Ca by using FHF,DCFHF,and DC-TDHF methods,and make a comparison among these different internuclear potentials.It is found that for spin-unsaturated systems,the tensor force has considerable modifications on the inner part of internuclear potential such that it affects the fusion cross sections,especially for sub-barrier collisions.

Although the effects of tensor force on fusion cross sections have been revealed,there are still many open problems on the influence of tensor force on heavy-ion reaction to be explored further.Here we discuss part of them from the perspective of this work:

· In nuclear structure studies,it has been shown that the tensor force has a strong influence on the shell evolutions of exotic nuclei.The shell structures are also very important for the studies on nuclear reactions,especially on fission and quasifission processes.Therefore it is particularly interesting and meaningful to investigate how the tensor affects the (quasi) fission processes,the corresponding fragments distributions,and the role of the shell structure.Such kinds of studies are in progress in our group.

· Up to now,the influences of tensor force on fusion reaction are only studied in those systems with spin-(un)saturated shells due to the absence of pairing effects.Recently,fusion reactions with exotic nuclei is of great interest both experimentally and theoretically.It is necessary and meaningful to extend FHF,DCFHF,and DC-TDHF to study reactions with neutron(proton)-rich nuclei by considering pairing correlations properly,aiming at not only the precise description of fusion reaction with exotic nuclei but also a microscopic understanding of their reaction mechanism.

· Recently,there are many experimental and theoretical works concerning the hindrance of the fusion cross sections at the extreme sub-barrier energies.One of the solutions proposed to explain this phenomenon is called the sudden approximation,in which the hindrance of the fusion cross sections is connected to the repulsive core of the internuclear potential.We have shown that the tensor force has a strong influence on the potential pocket.Thus the tensor force might have strong effects on the extreme sub-barrier fusion,which is worth being investigated in future.

Acknowledgments

This work has been supported by the National Natural Science Foundation of China (Grants No.11975237,No.11575189,and No.11790325) and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No.XDB34010000 and No.XDPB15).Part of the calculations are performed on the High-performance Computing Cluster of ITP-CAS and the ScGrid of the Supercomputing Center,Computer Network Information Center of Chinese Academy of Sciences.

ORCID iDs