基于欧拉-欧拉方法的气液两相流数值模型发展综述1)
高一博 耿琳琳 王 振 张振楠 张德胜 )
*(江苏大学流体机械工程技术研究中心,江苏镇江 212013)
†(大连理工大学数学科学学院,辽宁大连 116024)
**(中国石油大学(华东)储运与建筑工程学院,山东青岛 266580)
海洋中蕴藏着丰富的石油、天然气等能源资源,约占油气资源总量的34%[1],而其中70%处于深海区域,开发潜力以及开采难度十分巨大。为了解决我国油气对外依存度过高的问题,需要尽快推进我国深海油气勘探开发进程,深海油气开采已成为保障我国能源安全的重要举措。
现如今,在深海油气输运中,气液混输技术大幅简化了开采工艺流程,节省了管道铺设成本、提高了油井采收率,具有高效、节能、环保的优点,已逐渐成为深海油气输运的首选方案。深海油气的主要成分为天然气和石油的气液混合物,因此油气输送本质上是一种气液两相流混输的科学问题。
对于长距离输送管道,内部多相流受气液流量、管道尺寸及空间布置等多因素影响,呈现出多种流型。如图1所示,在竖直管道中存在五种常见流型:分散气泡流、段塞流、混状流、环形流、环形液滴流。而在水平管道中由于重力的作用,又表现为与垂直管道不同的流型,具体又可细分为分散气泡流、环形气泡流、拉伸气泡流、段塞流、分层流、分层波浪流等[2]。而且,在深海油气开采进程中,由于复杂的工况环境、瞬变的来流条件,以及含气率的日益升高,导致混输管内气液两相流动状态不断发生变化,具体表现为多种气液流型并存,相间结构及其分布状态时空各异,各种动力学参数、流动特性随流型转换频繁变化等等。因此,如何准确地预测这种复杂环境下的气液两相流动是油气输运数值仿真领域的关键科学问题。

图1 管内气液两相流型示意图[2]Fig.1 Gas-liquid two-phase flow pattern in pipe[2]
目前,在数值上处理气液两相流的方法主要分为欧拉-拉格朗日和欧拉-欧拉两种。欧拉-拉格朗日方法将液相视为连续的流体,将气相视为拉格朗日质点,通过求解质点的运动微分方程得到离散相在流场中的运动轨迹与运动状态。该方法的最大优点是可以得到离散气泡在流场中完整的运动信息,以及由于受力引起的尺寸演变;缺点是其仅适用于离散相体积分数比较低的多相流动,并且往往需要消耗巨量的计算资源。而欧拉-欧拉方法则引入体积分数的概念,将每一相都假定为可互相穿透的连续介质,每一相都拥有各自独立的压力场、速度场以及温度场等物理属性,在保证一定精度的前提下,相较于欧拉-拉格朗日方法大幅降低了计算成本,目前在多相流领域中被广泛应用。
此外,随着气液两相中含气率的升高,气泡与气泡之间会频繁发生相互作用,具体表现为由于气泡的聚并和破碎引起的气泡产生与消亡,这导致了气泡尺寸在流场中呈现多尺度分布特性。而在常规的欧拉-欧拉方法中,往往采用的是均一气泡直径,忽略了气泡的多尺度分布及泡间相互作用,从而导致常规方法对于高含气率气液流场的解析度有限。目前,能够较好预测气泡多尺度分布的方法是通过引入群体平衡模型(population balance model,PBM)来模拟气泡之间的相互作用。该模型也将在下文中进行详细介绍。
在本文中,将对欧拉-欧拉框架下气液多相流研究中所使用的主要相间力模型及其发展情况进行介绍。并针对该方法在深海油气混输过程中的高压高含气率特殊环境中的局限性进行阐述,展望其未来的发展趋势,以期为我国深海油气输运数值模拟研究的发展提供有益的参考。
1 相间力模型
正确描述液体中气泡的受力情况,对于研究气液两相流的复杂系统具有重要意义,而欧拉-欧拉模型模拟气液两相流动状况需要解析相间作用力来封闭控制方程。在油气混输过程中,一般忽略气液两相的相间传质作用,控制方程为
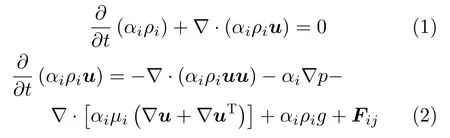
其中αi,ρi,ui分别表示为第i相的宏观体积分数、密度和速度,Fij表示气液两相的相间作用力,主要用于表示相间动量的传递,它实际上是多种力共同作用的结果[3]
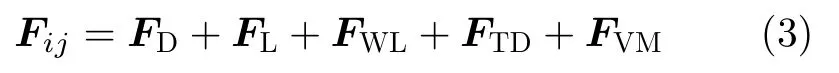
其中,等号右边分别代表五种不同的相间作用力,其产生机理如图2所示。FD代表曳力,是由气相与液相之间的相对运动引起的;FL代表升力,是由垂直于气泡运动方向的压差所引起的侧向力;FWL代表壁面润滑力,是由壁面附近的滑移速度产生的;FTD代表湍流扩散力,代表由液体湍动对气泡引起的牵引力;FVM代表虚拟质量力,是由相对加速度的变化而产生的力。相间力的选用会直接影响到数值计算的收敛性,所以进一步优化相间作用力模型是该方向的突破口[4]。
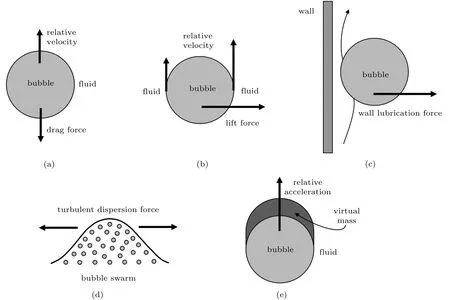
图2 气液相间作用力示意图[5]Fig.2 Illustration of the interphase forces in bubbly flow[5]
1.1 曳力
目前普遍认为曳力是气液两相间最重要的作用力,它来源于气泡与液体的相对运动,是两相间动量传递的主要作用力。曳力的大小取决于气泡的形状、流体的特性以及气液相对速度[6]。单个气泡所受到的曳力表达式为

式中,CD,ρl,ur和Ad分别表示气泡的曳力系数、液体密度、两相间的相对速度和气相投影面积。由式(4)可以看出,若要计算出曳力的数值,需要对曳力系数CD进行明确定义。但是对于不同流动状态的流场,曳力系数存在不确定性,因此研究者对于曳力模型的研究也就主要集中于曳力系数上。对气泡的曳力系数模型的描述通常引入一些无量纲参数,如气泡Reb(Reynolds数)、Eo(Eötvös数)、Mo(Morton数)、We(Weber数),并通常将曳力模型定义为它们的函数。表1中总结了文献中较为常用的气泡曳力系数模型。

表1 气泡曳力模型(续)Table 1 Bubble drag force models (continued)

表1 气泡曳力模型Table 1 Bubble drag force models
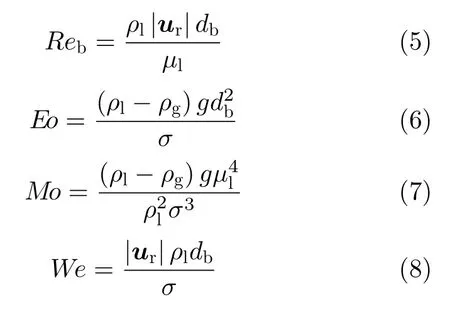
式中,db和ρg分别表示气泡的直径和密度,σ表示气液界面张力,g表示重力加速度。
现如今,例如Schiller-Naumann模型[7]、Grace模型[8]、Ishii-Zuber模型[9]、Tomiyama 模型[10]等曳力模型已被广泛应用于气液两相流数值模拟[11],并已植入商用CFD软件中供用户选择。Schiller等[7]在1935年提出的模型是最为经典的曳力模型,其根据气泡雷诺数的两个不同范围来分别定义曳力系数,对于Reb≤ 1 000的情况,CD定义为气泡雷诺数的函数,而当Reb> 1 000时,CD则定义为常数值0.44。Schiller-Naumann模型通常适用于尺寸小于2.5 mm的球形气泡[12],而对于较大的气泡尺寸则适合使用Ishii-Zuber模型。1979年Ishii等[9]利用混合物黏度的概念对液滴和颗粒的曳力关系进行了深入的研究,发现曳力系数可以用不同形状的气泡和不同的气泡流型加以区分,如扭曲气泡区域、帽状气泡区域和椭球气泡区域,此外,Ishii 等[9]、Miao等[23]和Xu等[24]还引入了气泡Eo,从而更准确地描述气泡形状与曳力的关系。同样是考虑了气泡形状,Grace曳力模型在考虑Eo的同时,还考虑了气泡Mo的影响[8]。
Tomiyama等[10]针对单个气泡的曳力系数进行了实验研究,考虑了气泡的形状,提出了一个具有一般性的曳力系数关联式,但是在将Tomiyama模型应用于多气泡系统时,应当考虑含气率对曳力的影响。另外还考虑了液体的污染程度,并根据液体的纯度提出了不同的相关性。Tomiyama等[10]提出的曳力模型已经在10-2 Simonnet等[13]通过实验研究了气泡与气泡之间的相互影响,通过分析较大含气率范围内的气泡群的运动状态,提出了适用于0%~30%含气率范围和纯水-空气体系的曳力关系。如图3所示,由于相邻气泡导致的气泡曳力减小,因此将局部含气率αg,loc和气泡平均直径db相关联。气泡状态变化的临界含气率为15%,在此处由均匀状态向非均匀状态过渡,曳力系数的比值也由线性变化转变为非线性变化。为了更好地描述变化的趋势,Simonnet等[13]在曳力关系式中加入了修正因子。出真实的流场。为此,研究者将压力的影响引入到了曳力模型中[25-26],Krishna等[25]认为压力对流场的影响主要在两个方面:一是压力的增加增大了气相密度;二是压力的增加增大了大气泡的破碎概率,减小了大气泡上升速度。因此在大气泡的曳力模型中添加了气相密度修正项 (ρg/ρg,0) ,从而考虑了操作压力的影响,然而,这种修正因子的引入高估了在较高表观气速和较高压力下的总体含气率。 图3 气泡曳力系数与局部含气率的关系[13]Fig.3 Bubble drag coefficient vs.local void fraction[13] Chen等[26]对压力范围0.1~1.0 MPa的气泡流进行了数值模拟,考虑了气泡聚并与破碎对气泡尺寸分布的影响,在分析Krishna等[25]引入的气相密度修正项的基础上,在曳力模型里添加了新的气相密度修正项 (ρg/ρg,0)0.25,得到的结果中不同压力下的局部气含率及轴向液速的径向分布都与实验结果吻合较好。Yang等[17]提出一种根据气泡尺寸分布的平均曳力系数模型,它同时考虑了小气泡的阻碍效应和大气泡的尾流加速效应,对于小气泡的考虑实质上是一种对高压环境下的曳力修正,因此可适用的范围更广。 Zhang等[18]在Roghair等[16]的气泡群曳力模型的基础上,基于冷态实验测量的整体含气率,在压力0.5~2.0 MPa范围内对气泡群曳力模型进行修正,采用了含有压力修正因子的曳力系数计算公式,适用于加压条件下改进的气泡群曳力计算。Mach 等[20]实验测定了四种不同压力(0.14 MPa,0.46 MPa,2.00 MPa,4.00 MPa)下的气泡尺寸分布和单个气泡曳力系数,量化了气泡尺寸分布与单个气泡曳力系数之间的关系。在气含率不变的情况下,压力的增加导致单个气泡的曳力系数减小。并且这些较小的气泡会引起边缘液体扰动,起到抑制湍流的效果,从而减少曳力。 Van Tran等[19]采用欧拉-欧拉模型模拟了压力在 0.1 MPa,1.5 MPa和3.5 MPa条件下的空气-水体系。采用了带有压力参数的修正因子修正曳力,并根据不同气体流量和压力下的实验数据,对压力修正因子进行了优化。修正后的PBM模型在合理的精度范围内较好地反映了空气-水加压鼓泡塔的流体力学特性。Van Tran等[21]测试了最高16 MPa下减压渣油与氢气的气液两相流特性,测量了密度、黏度、表面张力等物理参 Roghair等[16]认为通过实验同时测量多个相关参数存在大量的困难,因此采用直接数值模拟方法和欧拉-拉格朗日法,研究了密实气泡对气泡曳力的影响,并通过考虑局部含气率和单个上升气泡的相互作用提出了改进的曳力模型,适用的气含率最高可达45%。Van Tran等[19]认为在均相流区,气泡以小气泡为主,小气泡合并形成大气泡。因此为了综合考虑气泡群和尾迹对曳力系数的影响,将局部气含率作为影响因素加入到曳力系数中。 Gillissen等[14]考虑了大范围复杂泡状流和气泡变形的共同作用,采用格子Boltzmann法和浸没边界法,对三维周期域内浮力驱动的无质量球形气泡的悬浮进行了直接数值模拟。研究了在液体中上升的分散气泡群所受到的曳力,并得到了气泡曳力系数与气泡韦伯数和雷诺数的关系。 Yang等[15]通过气固能量最小多尺度模型考虑非均匀结构对相间曳力的影响,创建了双气泡尺寸(dual-bubble-size, DBS)模型,将气泡分为大小两种,通过大小气泡的气含率,直径和表观速度来描述气相的状态,通过不同尺度的能量耗散来封闭控制方程,并将能量最小原则作为稳定性判据。最终提出DBS曳力模型,该模型无须调整模型参数即可合理地预测径向含气量分布和两相流场。Guan等[22]在Yang 等[15]的基础上,对不同操作模式下的DBS曳力模型进行研究,计算了不同表观气速下的气含率和曳力系数,并将其一一对应,进一步提高了模型的预测精度。 上文中所介绍曳力模型通常只适用于常压条件下的气液两相流,对于高压环境下则无法反映数,通过拟合经验方程得到经验修正因子,并将修正因子加入到了Ishii-Zuber曳力模型中。 升力受流体剪切和气泡大小的影响,是一种沿着运动气泡的横向方向作用于气泡的力。由于其考虑了流体剪切对气相运动的影响,可用于稳定流动中球形气泡的横向迁移。有学者研究表明,为了减少计算量,在数值模拟中可以忽略升力的影响[26-28]。气泡的剪切诱导升力FL为 其中,CL表示升力系数,αg表示气相的体积分数,ul表示液相速度。与曳力一样,升力对气泡在流场中的横向分布也起着重要作用。数值和实验证明,升力方向的变化与变形气泡的尾流不稳定性有关,气泡的变形可以诱发升力符号的改变[29-30]。Hibiki等[31]对在各种流动条件下开发的升力现有模型进行了广泛的文献调查。与曳力的计算类似,针对不同升力模型的研究主要针对的是升力系数CL,现有的主要升力模型如表2所示。 表2 气泡升力模型Table 2 Bubble lift force models Saffman[32]首先对均匀剪切流场中单个球体的升力进行研究,并将升力系数定义为涡度雷诺数Reω的函数,适用于低雷诺数流的固体颗粒或气泡。Mei等[33]研究了均匀剪切流动中的球形气泡。通过在气泡表面施加不同的边界条件计算惯性迁移速度。利用Saffman给出的升力与迁移速度之间的关系,提出了在一定雷诺数范围下升力的表达式,适用于湍流自由剪切流中的小球形气泡。缺点是不能精确表示壁面上的非球形气泡的剪切升力。Moraga等[34]在此基础上提出了一种主要应用于球形气泡的升力模型,将气泡涡度诱导升力和剪切升力结合起来,从而综合考虑了尾流产生的涡流效应。 Tomiyama等[10]对甘油溶液中的单个气泡进行了实验研究,提出了CL关于气泡雷诺数Reb和修正的Eo′数的关系式,Tomiyama升力模型适用于椭球状到球帽状范围内的可变形气泡,并验证了当Eo′>10时升力方向会发生转变。 Legendre等[35]对CL进行了数值研究,并提出了适用于球形气泡的经验关联式,作为无量纲剪切速率(Sr)和气泡雷诺数Reb的函数。并提出了低雷诺数时气泡升力的变化不同于高雷诺数的情况,Legendre-Magnaudet升力模型的适用范围为 0.1≤Reb≤500 。 壁面润滑力是由靠近壁面的气泡周围速度分布的变化所产生的力[36],受气液表面张力的影响,防止气泡附着在壁面上[37]。其数学表达式为 其中,CWL表示壁面润滑力系数,urw表示相对速度在壁面处的切向分量,nw表示壁面上的单位外法向量。表3总结了研究者现已提出的壁面润滑力系数计算方法。 表3 气泡壁面润滑力模型Table 3 Bubble wall lubrication force models Antal等[36]首先将壁面润滑力的概念引入到球形气泡,假设了球形气泡和层流条件,将壁面润滑力与气泡直径和壁面距离相关联。Antal模型适用于在气泡到壁面的距离ywall≤5db的范围。Tomiyama等[38]对甘油流动中的气泡进行研究,提出了基于管道直径Dpipe和气泡Eo的壁面润滑力模型,并将气泡Eo分为四个区间区分了不同大小的壁面润滑力,具有很好的计算精度,是一种经典的壁面润滑力模型。在2002年Tomiyama等[30]又对气泡的横向运动机理进行研究,在1 ≤Eo≤ 33的范围内重新定义了壁面润滑力,并使其摆脱了管道直径的限制。Hosokawa等[39-40]对不同浓度甘油溶液中的气泡进行了实验研究,发现壁面润滑力系数不仅取决于气泡Reb和Eo[39],还与气泡Mo数有关[40]。Hosokawa模型的适用范围仅限于气液两相泡状流,并且已经在2.0 ≤Eo≤10.0,Reb< 10,以及 -6.0 ≤ lgMo≤ -2.5,0.4 ≤Reb≤ 65的范围内得到了验证。 Frank等[41]修正了Tomiyama的壁面润滑力模型,使该模型脱离了流型的限制,此外还引入了两个系数,一个是阻尼系数Cdamp, 另一个是截断系数Ccut-off。Cdamp决定了壁面润滑力的相对大小,Ccut-off决定了壁面润滑力起作用的相对距离,这两个系数的引入使得Frank模型可以更准确模拟壁面润滑力。 当连续相速度的连续随机波动作用于气泡时,就产生了湍流扩散力。它受液体中湍流涡对分散气泡的影响,由连续相湍流涡流对分散相的综合作用组成,在气泡体积分数的径向分布中起着重要作用[42]。现行的湍流扩散力模型分为两类:Lopez de Bertodano模型[43]和 Favre-averageddrag(FAD)模型[44]。 Lopez de Bertodano[43]通过假设气泡运动近似于空气分子在大气中的热扩散而对简单湍流弥散力建立模型 其中,kl表示液相的湍动能,湍流扩散力系数CTD的取值在0.1~0.5之间[44]。 Burns等[45]通过将Favre平均值应用于流体曳力来建立的湍流分散力模型为 其中,Prα表示体积分数离散的湍流普朗特数,γl表示液相的运动涡流黏度。 其中,斯托克斯数St是由气泡的松弛时间tb和涡松弛时间te共同定义的 虚拟质量力是由于加速的气泡对液体所做的功而产生的。此外,虚拟质量力还可以表现为由于气泡在连续相中加速时所产生的额外曳力而产生的力。对于加速流动的两相系统,当两相之间密度相差很大时,虚拟质量力起到十分显著的作用[46]。虚拟质量力可表示为 CVM是虚拟质量力系数,它取决于流型、离散相的几何形状以及体积分数。在一般的数值研究中,采用的是固定的虚拟质量力系数。如球形气泡的虚拟质量力系数通常为0.5[47]。然而,对于特定的条件,例如管直径大于0.15 m的情况,虚拟质量力对模拟结果的影响可以忽略[47-48]。 综上所述,欧拉-欧拉方法,通过建立不同的相间力模型研究气液两相的流动形态,数值模拟的效率和准确性取决于合适的界面力模型,一些研究者在求解欧拉-欧拉控制方程时同时使用了不同的相间力[19-21]。由于曳力对气泡运动的影响明显大于其他相间力的作用[49],有研究者仅使用曳力模型来预测气液两相流体动力学性质[26,50-51]。目前尽管这些相间力的研究已经取得了很大进展,但在数值模拟中相间力模型的普适性仍有待进一步探究。 目前,在气液两相流的模拟中,较常使用的欧拉-欧拉方法往往采用的是平均气泡直径的处理方式,然而在现实的气液两相流动过程中,气泡的产生和消失、气泡的合并和破碎现象非常普遍,这导致了气泡尺寸呈现多尺度分布,并且气泡的大小分布还会随着多相体系的相间传递现象而发生变化。因此,在模拟气液两相流时,需要对气液两相流中气泡尺寸分布进行更合理的预测,进而能够获取界面区域浓度和动量曳力项来更新计算界面传递项,从而对气液两相流的动态行为进行更准确的计算[52]。针对以上流场特征和仿真目标,群体平衡模型通过求解气泡数密度输运方程来考虑气泡破碎聚并的影响,且通过耦合欧拉-欧拉模型对气液两相流进行模拟已成为气液两相流领域研究的热点。以下将对群体平衡模型基本理论进行介绍与讨论。 群体平衡模型最早由Hulburt等[53]提出,近年来该模型在气液多相流的模拟中应用越来越广泛。对于气液两相流体系,群体平衡模型的有效利用能够描述不同尺寸气泡在液相中的分布,对于更深入了解气液多相流运动机理有很好的帮助。考虑气泡破碎聚并的群平衡模型的输运方程为 其中,Gv表示气泡的生长速率,BA和DA是与气泡合并有关的产生项和消失项,BB和DB分别是与气泡破碎有关的产生项和消失项,V表示破碎后子气泡体积,n(V)表示体积为V的气泡数密度函数。 其中,V′表示破碎前气泡体积,gb(V′) 表示破碎频率,βb(V|V′) 表示气泡破碎的概率密度函数,Γc(V,V′)表示气泡聚并速率,现有的聚并破碎模型一般需要碰撞频率hc和聚并效率λc的模型来描述聚并频率。表示为 破碎模型一般表示为气泡破碎频率gb和子气泡尺寸分布βb的模型来模拟破碎,这些模型的建立与流体和流动属性有关[54]。表4和表5中列出了一些适用于气泡流的聚并和破碎模型。 表4 气泡聚并模型Table 4 Bubble coalescence models 表5 气泡破碎模型Table 5 Bubble breakage models 气泡碰撞主要有四种机制:湍流诱导碰撞、浮力诱导碰撞、尾迹卷吸碰撞和黏性剪切碰撞。Coulaloglou等[55]首先提出了气泡的湍流诱导碰撞机制,假设聚并主要在平缓的相界面上进行,还必须满足碰撞的条件,并且充分接触以便在这些过程中发生膜排出、膜破裂和合并过程。Coulaloglou-Tavlarides聚并模型同样适用于圆球状的液滴和小于湍流微尺度的液滴,该建模思想被后来的研究者所采用。Prince 等[56]详细定义了气液体系中发生气泡聚并的必要因素,考虑了由湍流、浮力和黏性剪切引起的碰撞,并假设不同机制的碰撞是累积的,用气体分子运动论的方法在Coulaloglou等[55]的基础上建立了适用于气泡-水体系的碰撞频率模型。 Luo等[57]基于能量守恒分析提出了估算气泡接触时间的模型。模型只能对小尺寸的液滴给出很好的预测。Lehr 等[58]根据前人的理论并通过实验发现,当两个气泡之间的相对速度大到一定程度时,发生碰撞后并不会产生聚并行为而是相互弹开。根据这一现象假设气泡聚并发生的条件是碰撞速度低于一个临界值ucrit,当气泡碰撞速度高于临界值时气泡发生反弹而非聚并,Lehr模型同时考虑了两个气泡相对速度和流体湍流涡两种碰撞机理。 Zhang等[18]针对压力高达2 MPa的空气-水体系,考察了压力对气液两相流动的影响,认为压力对气泡的聚并也有着一定的影响,根据冷态实验数据,在Luo聚并模型的基础上新增了修正系数Ce=0.319ln(ρ/ρ0)+0.665 ,由于是通过数据拟合得到,该模型属于一种半理论半经验的模型。 气泡破碎主要有四种机制:湍流涡碰撞,黏性剪切力,尾涡剪切脱落,大气泡表面不稳定。这四种机制中,以湍流涡碰撞为主,Coulaloglou等[55]根据各向同性湍流理论,通过假定子液滴的运动与湍流的运动具有类似的性质,从而确定了破碎时间,认为液滴破碎的决定条件是液滴湍动能大于表面能,并且预测破碎产生的子液滴尺寸呈现正态分布。然而对于气泡-水体系,Coulaloglou等[55]的模型并不能很好地预测。Prince等[56]对水中气泡的破碎进行实验研究,忽略了小于0.2db的湍流涡体对气泡破碎的影响,将气泡和湍流涡的碰撞过程类比为气体分子运动,认为气泡破碎速率等于气泡和湍流涡体碰撞频率与破碎效率之积。 Luo等[57]基于Prince等[56]的理论,认为在气液两相中湍流涡的湍动能量大于气泡破碎后表面能的增量时才会引起破碎,并直接由气泡破碎速率函数导出子气泡尺寸分布的表达式,因此当子气泡的尺寸趋近0时,气泡的破碎概率会无限增加。Laakkonen等[59]为了避免这一现象的发生,提出一种在数学上更简洁的尺寸分布模型,使无限小的子气泡和等于原始气泡的子气泡的破碎概率为0,更有利于计算。Lehr等[58,61]和Laakkonen等[59]将压力的影响加入到破碎模型中,认为只有在湍流涡产生的动压大于破碎后最小气泡的内部压力时,母气泡才会发生破碎。气泡破碎概率密度为湍流涡动压与气泡表面力的比值。 自从群体平衡模型被引入到多相流模拟中来,模型的建立和求解等方面都得到了较大的发展,并根据对气泡破碎和聚并机理的研究,建立了许多针对不同机理的气泡破碎或聚并模型,但对于适用于加压条件的模型尚处于理论研究阶段,文献中报道压力的变化主要影响气泡的破碎行为,对气泡聚并行为影响较小[62]。 Wang等[63]认为湍流涡碰撞和大气泡表面不稳定性导致的气泡破裂是主要的。通过将这两种机制产生的速率相加,计算出总的气泡破裂速率。Yang等[17]在此基础上考虑操作压力对气泡破裂的影响,通过实验测量气体密度对不同大小气泡破碎率的影响,将拟合得到的经验压力修正因子加入到气泡破碎模型(图4)。 图4 气体密度对不同大小气泡破碎率的影响[17]Fig.4 Effect of gas density on the bubble breakup rate for different bubble sizes[17] Xing等[60]对破碎过程中气泡/液滴颈部的内部流动进行了机理分析,认为气泡/液滴内部的流动行为强烈依赖于压力或气体密度,基于这一机理,提出了一种气泡和液滴的统一破碎模型。Zhang等[64]系统地研究了群体平衡模型的通用性,通过静态应力分析、气泡颈部的界面应力和黏性流动曳力充分描述变形气泡内的流动,结合内外压差对气泡颈部的影响,重新解释了气泡破裂的因素,提出一种不需要针对特定的模拟情况调整模型参数的气泡破碎模型,并已证明在0.1~1.0 MPa的压力范围内的良好适用性。 Van Tran等[65]提出气泡的破碎率随着压力的增加而增加,并强调在压力较高的情况下压力修正因子的重要性,基于Lehr等[61]提出的破碎模型进行改进,加入了修正系数 (P/P0)1.5,在0.1~3.5 MPa的压力范围很好地预测了均匀泡状流区的总气含率和平均气泡尺寸。Van Tran等[66]比较了常用的Luo,Lehr和Wang模型在总破损率、子粒尺寸分布和计算时间等方面的优劣。在Luo破碎核的基础上,考虑了压力对气泡破碎率的影响,提出了一种基于密度变化的修正系数0.35(ρg/ρg,0)0.3,并验证发现改进后的Luo模型更适用于加压环境。 高含气率下气液多相流的数值模拟研究对于深海油气混输具有重要意义。采用欧拉-欧拉模型耦合群体平衡模型的数值方法已成为该领域研究的热点与重难点。然而,该数值方法的准确性往往依赖于众多子模型的封闭与选取,在过去的几十年里,众多研究者在该方面做了大量的工作,本文进行了如下总结。 (1)回顾了现有的气液相间力(包括曳力、升力、湍流扩散力、壁面润滑力和虚拟质量力)模型,对各个模型的相关理论与发展进行了系统总结。结果表明尽管相间力模型在过去的几十年中已取得长足进展,但仍存在准确性依赖于经验性的可调参数、模型普适性有限、计算量大等问题,且面对深海高压高含气率的特殊气液混输应用需求,相间力模型的发展仍有待深入研究。 (2)对气液流动的群体平衡模型的子模型进行了总结,包括气泡的聚并模型和破碎模型,大量研究集中于气泡的破碎模型,大多数的破碎模型都基于气泡与湍流涡碰撞的假设,但是忽略压力的因素导致模型与实验结果存在一定差距,因此,建立考虑压力对气泡破碎的影响机理并且能够统一描述气泡破碎的模型,对于群体平衡模型的发展将有重要的意义。 (3)压力的变化对于气泡的动力学模型有着很大的影响,总结了一些在高压环境下对气液两相数值模型的处理方法,通常是将压力的影响引入到曳力模型与破碎模型中,对其进行修正,但多为经验性的,因此还需要进行针对性研究使模型具备良好的普适性。 综上,目前针对相间力模型以及群体平衡模型的扩展是比较前沿的,在许多文献中都可以找到很多不同的思路,并都能得到很好的应用和验证。但是在油气混输的复杂环境下,常规相间力模型和群体平衡模型都需要进行特殊处理。尽管在建立和创新气液相间力和群体平衡模型方面已有学者做了大量的工作,但对于深海环境油气混输等特殊工况下的气液两相流数值模拟,仍需进一步努力以提高模型的适用性与准确性。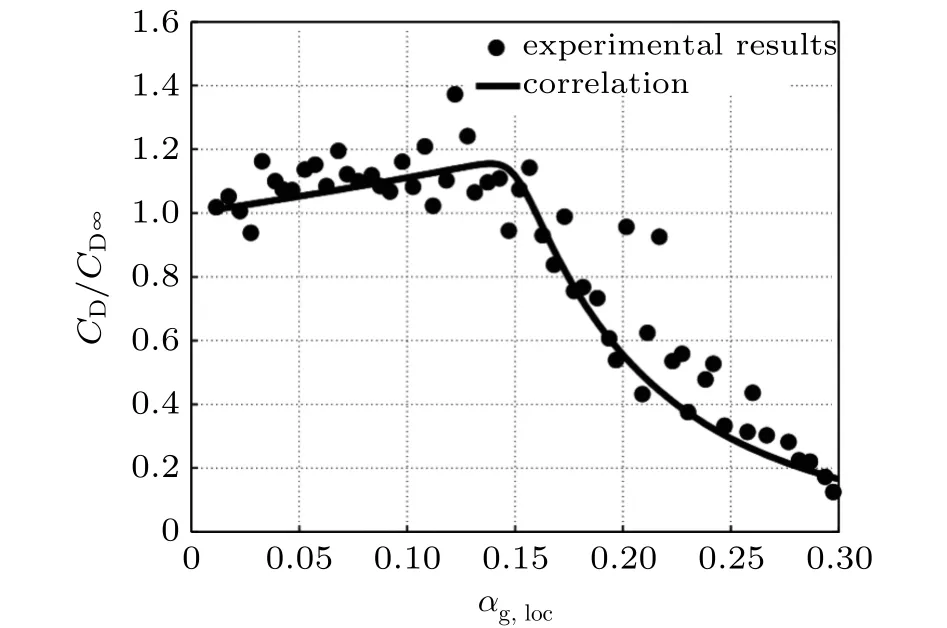
1.2 升力

1.3 壁面润滑力


1.4 湍流扩散力



1.5 虚拟质量力

2 群体平衡模型




2.1 气泡聚并模型
2.2 气泡破碎模型

3 结语

