基于SCADA数据海上风电场解析尾流模型可靠性与尾流叠加研究
张 皓,易 侃,张子良,许 昌,李健英
(1.中国长江三峡集团有限公司科学技术研究院,北京 100038;2.河海大学 能源与电气学院,江苏 南京211100;3.上海勘测设计研究院有限公司,上海 200434)
0 引言
风能作为全球能源市场上主要的可再生能源之一,在温室气体减排及能源电力系统可持续发展方面发挥着重要作用。截至2020年底,全球风电装机总容量达到744GW,2020年新增装机93 GW,与上一年同比增长约50%[1]。随着各国和地区“碳达峰”和“碳中和”目标的相继提出,预计未来30a风电对全球发电量的贡献将增至18%[2]。
在不断增长的风能市场中,由于陆上风电用地限制等因素,海上风电取得了较快的发展。但是,由于海洋空气环境湍流强度较低,上游风力机形成的尾流区域的恢复速度明显慢于陆上风电场,进一步加剧了下游风力机的功率损失[3]。因此,海上风电场尾流效应的科学准确评估是进行风电场微观选址和排布设计的关键,是实现海上风能资源精细化评估和高效利用的重要基础。
风电场尾流评估主要采用计算流体动力学(CFD)模型和解析模型。CFD模型能够获得较为准确的结果,但是对一个包含多台风力机的海上风电场进行CFD模拟所耗费的时间成本往往是工程所不能接受的[4]。因此,解析模型是目前风电工程中使用最多的方法。文献[5]结合一维动量定理对Park模型进行补充,得到工程上最为广泛应用的Jensen模型[6]。Larsen G C依据边界层方程推导出Larsen模型[7]。Frandsen S根据动量守恒定理得到Frandsen模型,该模型假设与Jensen尾流模型基本一致,但是在推导过程中选用的控制体不同[8]。为了获得更加接近真实情况的尾流分布模型,Bastankah提出了Gaussian模型,在模型中引入了尾流横截面速度亏损服从高斯分布这一条件[9]。解析尾流模型所需计算资源较少,但是其精度严重依赖于经验参数在不同工况下的调整,而且模型在推导过程中运用了大量假设和简化,使模型难以获得较为精确的模拟结果。在风电场微观选址阶段,通常采用上述几种解析模型对风电场的尾流效应进行定量描述,但是在实际应用中,不同模型的准确性及适用性往往存在一定差异。
另一方面,在对整个风电场进行尾流评估时,还需要考虑尾流叠加效应。近年来,风力机单机容量呈不断上升趋势,其轮毂高度和叶片长度也随之增长。风力机扫风面积的增大使得其尾流效应的影响范围也随之增大,进一步加剧了各风力机尾流区的相互影响。目前,对于风力机尾流相互影响机理和叠加计算的方法研究还存在很大不足。本文拟采用海上风电场的实测数据对尾流叠加现象进行分析并进一步探究其规律。
通过解析尾流模型准确评估尾流效应对于风电机组科学选型、排布方案优化、运行安全保障、整体发电量提升至关重要。本文利用海上风电场运行数据,对常用解析模型进行可靠性验证及对比分析,并进一步探究尾流叠加效应的演变规律。
1 风电场SCADA数据预处理
SCADA数据的准确性是风电机组实现优化运行、状态分析、尾流评估等过程的重要支撑[10]。在采用SCADA原始数据进行分析之前,需要对数据进行预处理,以尽可能识别并剔除异常数据。首先分别对原始风速及功率数据进行统计分析,剔除明显偏离正常值的点及数据缺失点(图1),剔除后的数据统计结果如表1所示;其次,将处理后的风速及有功功率数据进行综合分析,并与理论功率曲线进行对比,将明显偏离理论曲线的数据点确定为异常点并删除。
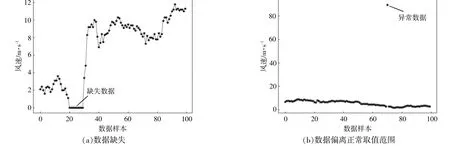
图1 数据异常种类示意图Fig.1 Schematic diagram of data anomaly types
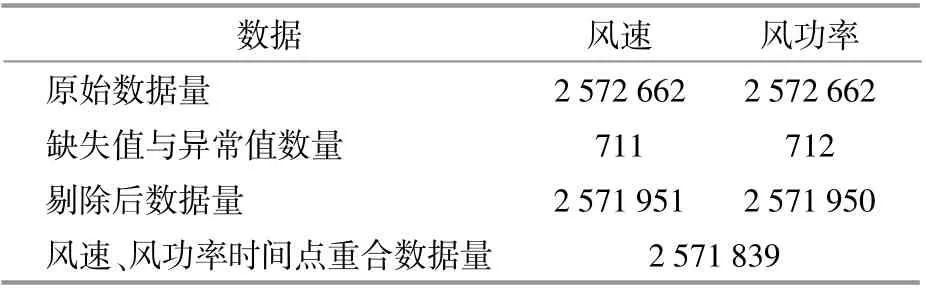
表1 原始风速及功率数据统计结果Table1 Statistical results of original wind speed and wind power data
图2所示为原始风速与有功功率的对应关系。
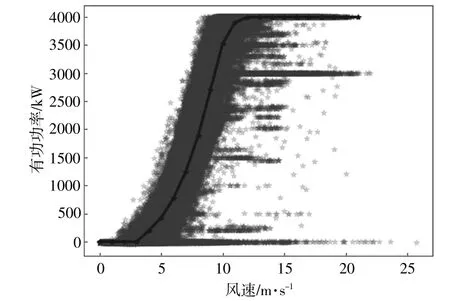
图2 风速-有功功率原始数据散点图Fig.2 Scatter plot of original wind speed and power data
为了消除异常点,采用单隐含层神经网络对SWT-4.0-130型号风力机的理论功率曲线进行拟合。风速及理论功率分别对应网络的输入与输出,网络训练采用梯度下降算法,精度达到一定要求后训练结束,得到风力机理论功率曲线(图2黑色曲线)。在此基础上,将实际风速数据输入神经网络,通过计算即可获取对应的理论预期功率值,并将实际有功功率与理论预期功率进行对比,二者偏差过大即可判定为异常值。偏差的合理范围随风速大小而变化,SWT-4.0-130风力机偏差设定如表2中所示。

表2 SWT-4.0-130风力机风速-有功功率对应关系合理区间Table2 Reasonable range of wind speed and power correspondence of SWT-4.0-130wind turbine
处理之后的数据统计结果如图3所示。由图3可知,大多数明显偏离理论功率曲线的异常数据点已被自动丢弃,表明数据预处理过程达到预期效果。
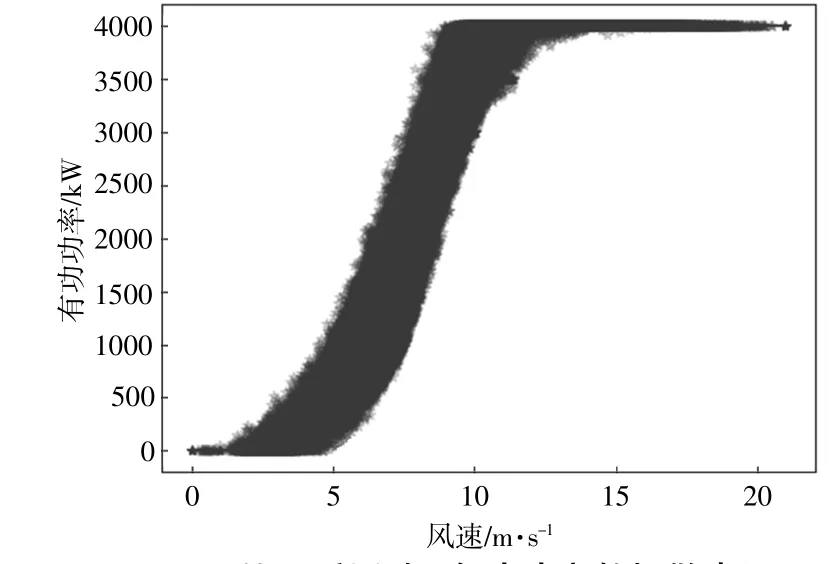
图3 预处理后风速-有功功率数据散点图Fig.3 Scatter plot of wind speed and power data after data pre-processing
2 解析尾流模型可靠性验证及分析
本文采用工程常用的Jensen,Frandsen和Gaussian解析模型对尾流效应进行模拟,并结合下游风力机实测数据对各模型模拟结果进行可靠性验证,依此探究各模型在海上风电场尾流模拟中的可靠性。以选定风电场54和55号风力机为研究对象,来流风速设定为6m/s,两台风力机间距为580m,其布放位置如图4所示。

图4 选定风电场风力机排布示意图Fig.4 Layout diagram of wind turbines in the wind farm
由于选定的两台风力机呈风向117°布置,在此风向附近下游风力机将受到上游风力机尾流效应影响。因此,本文选定风向为77~157°内共计5404个时间点的数据进行分析,图5所示为选定风向范围内的风速玫瑰图。
各尾流模型参数设置见表3,下游风力机速度亏损比率及功率亏损比率如图6,7所示。图中:极轴对应下游风力机与上游风力机的风速比值或功率比值,为0~1;极角对应实际风向与117°风向所呈夹角,设定顺时针为正;由于两台风力机间距不变,极径保持恒定。
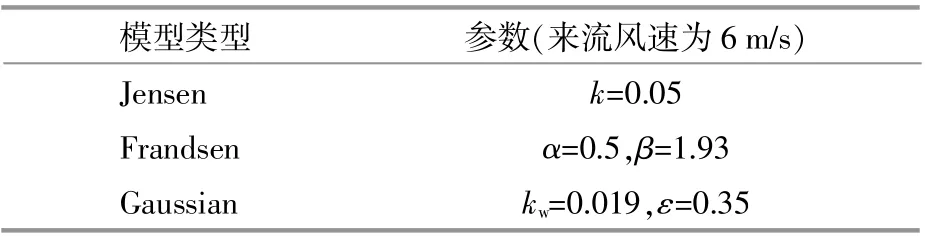
表3 各尾流解析模型参数设置Table3 Parameter settings of each wake analytical model

图6 各模型风速亏损模拟结果Fig.6 Wind speed loss simulation result of each wake model
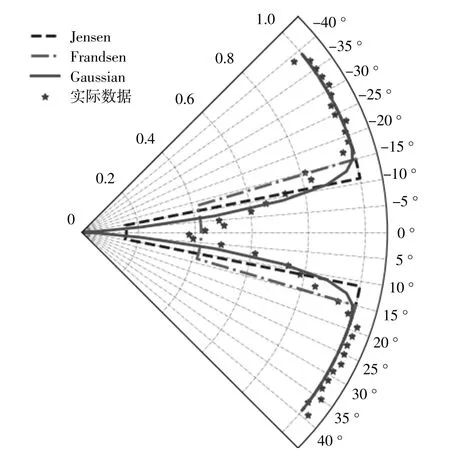
图7 各模型功率亏损模拟结果Fig.7 Wind power loss simulation result of each wake model
由图6,7可知:后排风力机风速实际亏损约为前排风力机的40%,而功率亏损最为严重时超过60%;Jensen模型在尾流中心区域附近的风速模拟结果能较为准确地反映实际情况,而Frandsen模型的模拟结果与风速实测情况相比低估了约10%。与Jensen和Frandsen模型相比,Gaussian解析尾流模型随风向演化规律更符合实测结果,即风速及功率衰减率在极角为0°时均为最大,此时风向与风机排布方位完全一致,尾流效应最为明显;当极角逐渐偏离0°变化时,风速及功率衰减率逐渐变小;当风向偏离程度较大时,风速及功率衰减率达到最小或者为0,此时尾流效应较弱或者消失。
通过经验公式推导的Gaussian尾流模型能够基本描述选定风电场内尾流随风向的演化规律,但是仍存在一定误差,因此该模型在参数设定上仍需要进一步改进及完善。为此,本文提出的Gaussian模型参数设定如下:
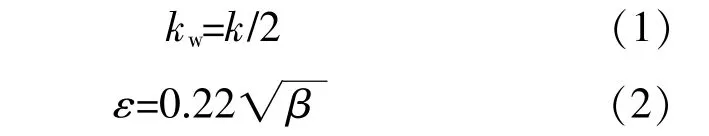
式中:k为Jensen模型尾流区膨胀速率;β为风轮后压力恢复至大气压处尾流截面面积与风轮面积的比值;kw为Gaussian模型尾流区膨胀速率;ε为初始标准偏差系数。
采 用 式(1),(2)进 行 修 正 后 的Gaussian模 型的模拟结果如图8,9所示。

图8 修正高斯模型风速亏损模拟结果Fig.8 Wind speed loss simulation result of modified Gaussian model
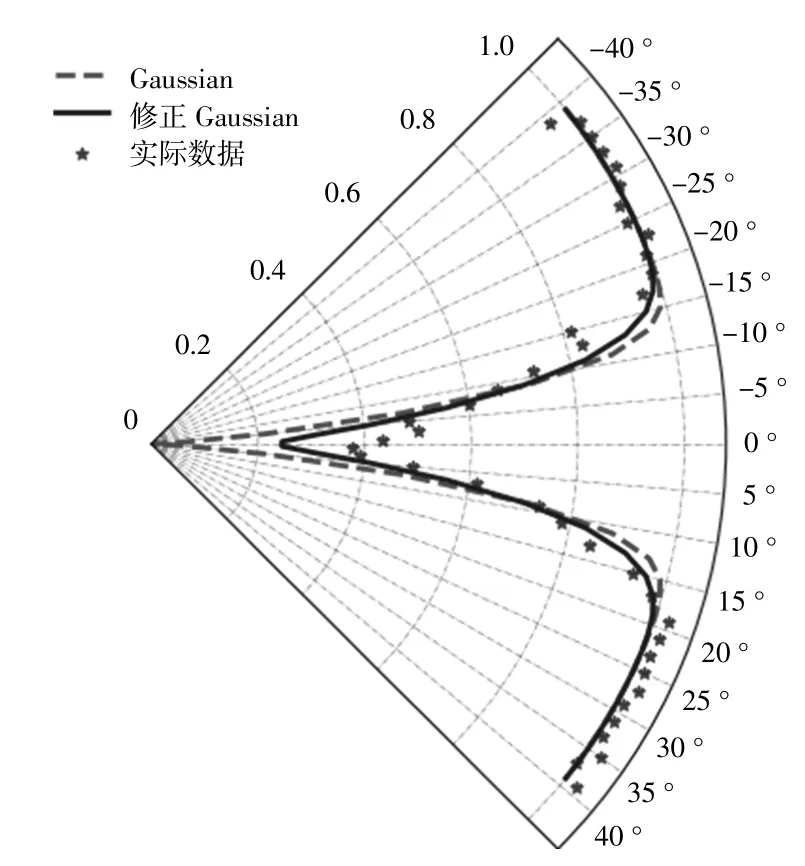
图9 修正高斯模型功率亏损模拟结果Fig.9 Wind power loss simulation result of modified Gaussian model
为了进一步衡量修正后的Gaussian模型的准确性,采用式(3)对所述尾流模型的模拟精度进行评价,评价结果见表4。
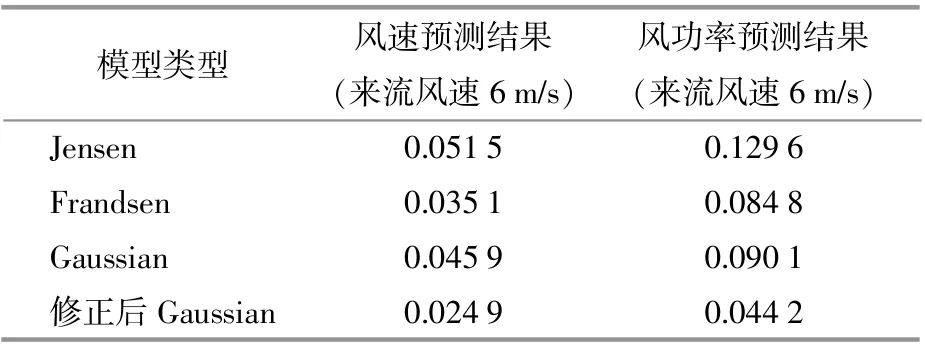
表4 各解析模型误差指标对比结果Table4 Error indexes comparison result of analytical models
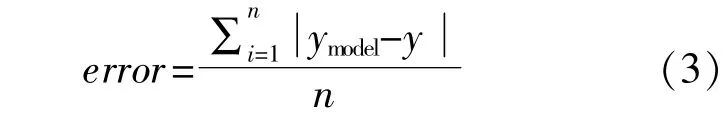
式中:ymodel为尾流模型模拟值;y为实际值;n为风向区间个数。
由表4可知,修正后的Gaussian模型的模拟精度相比原Gaussian模型提升约50%,取得了最高的模拟精度。为了进一步验证所提参数选取方案的适用性,在来流风速为8m/s和10m/s的情况下进行重复试验,修正后的Gaussian模型均能取得较高精度。因此,本文所提的Gaussian尾流模型参数选取方案能够适用于该海上风电场的尾流评估。
3 多台风力机尾流叠加特性
为了进一步考察海上风电场内的尾流叠加特性,本文拟采用实测功率数据对尾流叠加现象进行分析并进一步探究其规律。图10为场内4组平行等间隔布置风力机的功率衰减示意图。图中横坐标为风力机沿自由来流方向上的排列顺序,纵坐 标 为 第i(i=1,2,…,7)排 风 力 机 与 第 一 排 风 力机有功功率之比值,即功率衰减比率指标。风向变化为0~20°,其中风向为0代表实际风向与风力机排布方向完全平行。由图10可知,对于后排风力机而言,由于上游风力机的相对位置随风向而变化,因此受尾流效应的影响程度也随之变化,当风向较小,即来流方向与风力机排布方向一致时,尾流效应最为强烈,当风向逐渐变大时,尾流效应逐渐减弱,各风力机功率衰减也逐渐减弱。

图10 不同位置风力机在不同风向下的功率衰减实测情况Fig.10 Wind power loss for different wind direction and for different wind turbine position
在工程应用中,通常在对单个风力机尾流建模的基础上采用尾流叠加模型进行尾流叠加分析,常用的尾流叠加模型包括平方和模型及能量守 恒 模 型,分 别 如 式(4),(5)所 示。

式中:vfree为自由来流风速;vi为第i台风力机处风速;vj为第j台风力机处风速;vij为在第j台风力机尾流影响下第i台风力机处风速;s为上游风力机台数。
结合修正后的Gaussian模型及尾流叠加模型即可获取各排风力机处的预期风速情况,再通过标准功率曲线计算即可获取风功率预期衰减规律,最终模拟结果如图11所示。由图11可知,功率损失模拟结果均随着风力机排数逐渐递增并趋于平缓,其原因在于常用的尾流叠加模型并没有考虑湍流强度的变化过程。因此,在工程实际中尾流叠加模型的运用还需要在原始模型的基础上进行修正,以体现湍流强度变化导致的能量掺混过程。
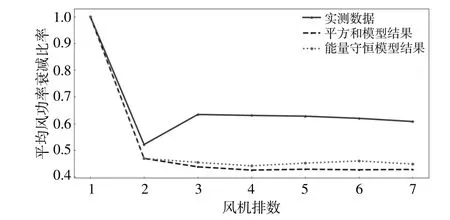
图11 49~55号风力机尾流叠加模型拟合结果Fig.11 Wake superposition result of wind turbines49~55
4 结论
本文针对海上风电场尾流效应,利用现场实测运行数据对工程中常用的解析尾流模型进行了可靠性对比验证,提出了更加适用的尾流模型参数选取方案,并进一步对尾流叠加现象进行深入分析,得到以下结论。
①结合风力机标准功率曲线所设计的适用于SCADA数据的预处理算法能够取得较好效果。
②在选用的几类常用解析尾流模型中,Gaussian尾流模型的模拟结果最符合现场实测尾流演化规律,且采用本文所提的参数选取方案进行修正后的Gaussian尾流模型的精度较之前约提升50%。
③选用的尾流叠加模型的模拟结果均无法正确表征现场实测功率衰减变化规律,需对尾流叠加模型结果进行修正,以进一步考虑湍流强度变化带来的影响。

