基于双树复小波的齿轮副裂纹故障检测方法

王天阳 陶学恒 代 鹏 冉海风

（1 大连工业大学 机械工程与自动化学院， 辽宁 大连 116034）

（2 安徽工程大学 机械与汽车工程学院， 安徽 芜湖 241000）

0 引言

直齿轮副因其具有瞬时传动比稳定、传动效率高、使用寿命长等优点，被广泛应用在现代机械工业传动机构中[1]。但因为齿轮副的制造安装误差、疲劳磨损、载荷突增、润滑失效等因素，常常造成齿轮副的故障。其中，齿根裂纹就是齿轮副常见故障之一。齿轮齿根出现裂纹，将大大影响齿轮副的传动精度，增加齿轮箱的振动与噪声，降低齿轮副传动NVH（Noise、Vibration、Harshness）性能，严重时将导致齿轮副传动失效[2]。

在旋转机械的故障诊断中，由于受周围环境、传感器质量和信号传输过程的影响，被检测物体的信号中往往混杂着各种噪声，有的噪声干扰甚至大于实际信号，这给信号中的特征信息提取带来极大难度。因此，在提取特征信息之前，必须对信号进行降噪。小波阈值降噪作为工程实际中常用的降噪方法，通过保留有效信号系数，减小甚至剔除噪声系数，以求得有用信号的最优估计；该方法结构简单、收敛速度快、降噪效率高，被广泛应用在机械振动信号的降噪领域[3]。但是，随着机械系统的复杂性提高，多机械系统协同作业，所产生的振动信号愈发复杂，在使用小波变换降噪时，对信号的分解难度增大；并且，滤波降噪要求对所有信号进行二进度尺度分解，这显然对信号特征的识别是不利的[4]。所以，专家学者们不断提出各种改进的小波滤波降噪方法，以满足复杂信号降噪的要求。吴定海等[5]针对环境噪声因素淹没故障早期所产生的微弱信号问题，提出了一种基于小波包变换的重叠块阈值降噪方法。华伟等[6]将多小波降噪方法应用到齿轮箱的断齿故障诊断中，利用小波变换的平移不变性，使降噪效果得到一定提升。Wang 等[7]将QPMZ-IⅡ型齿轮箱的振动信号利用小波变换降噪处理，并对降噪后的信号进行故障诊断。刘小峰等[8]基于小波包理论提出经验模态分解法，并在齿轮箱故障实测数据上得到应用。Jena 等[9]采用改进的小波降噪算法与有源噪声消除相结合的方法，对齿轮箱的健康状态进行了检测。Havale等[10]将小波变换与深度学习模型组合，制定了一种基于机械学习的齿轮箱的故障诊断模型，在该模型中，小波变换作为降噪手段对振动信号进行预处理，降噪后的信号作为学习模型的输入。孙海亮等[11]在研究轧机齿轮故障诊断问题时，提出一种基于多小波自适应的分块阈值降噪方法。小波阈值降噪方法改善了Fourier 变换困难的问题，在机械振动频谱中减小了杂频幅值，使得故障信号得以凸显；但小波阈值基函数确定后，在不对中振动信号降噪过程中易造成能量泄漏，缺乏足够的自适应性。为此，各学者又接连提出自适应性的小波降噪方法。Feldman[12]在Hilbert 变换的基础上提出Hilbert 振 动 分 解（Hilbert vibration decomposition，HVD），HVD 基于振动信号的瞬时频率和包络幅值，在保留分解精度的同时保证幅值不失真，分解效率和分解精度较高，常被用于机械系统在变工况下运行所产生的非平稳信号降噪处理。冯志鹏等[13]将HVD 降噪方法应用到行星齿轮箱的故障诊断中。唐贵基等[14]将改进后的HVD 方法应用到机械油膜涡动故障诊断中。孙熠等[15]将HVD 与1.5 维谱结合，并将该降噪方法应用到滚动轴承的故障诊断中。

目前，针对齿轮副齿根裂纹的理论研究已趋于成熟，但在对故障齿轮副实验数据的采集、处理与分析方面存在欠缺，难以根据实验数据对齿轮副健康状态进行有效评估。并且，小波变换隔点采样会丢失部分信息，小波滤波器不理想的截止性质会导致信号分解和重构过程中产生不真实的频率成分，造成小波分解系数不能准确地反映状态信息，使特征信息的提取效果受到影响。骨永刚等[16]中验证了双树复小波对斜齿轮副振动信号降噪的有效性，但缺少对比实验，没有采用其他信号降噪方法作为比较，难以量化双树复小波方法的性能。并且其降噪模型复杂，难以得到推广和应用。为此，本文中针对直齿轮副振动信号的降噪问题，提出利用4层双树复小波降噪方法，利用双树复小波的近似平移不变性和完全重构性对含噪信号进行有效降噪。利用常用的硬阈值函数和软阈值函数降噪方法与双树复小波降噪进行了对比实验，利用信号的信噪比和均方根误差指标量化双树复小波降噪方法对含噪信号的处理效果。降噪模型框架简单，计算负荷增量小，利于推广和普及，可为工程实际问题提供参考。

1 信号降噪

1.1 小波阈值降噪

为添加对比实验，利用Donoho 等[17-18]提出的硬阈值降噪和软阈值降噪算法，比较不同降噪手段对齿轮箱振动信号的处理效果。具体的硬阈值和软阈值函数表达式如下：

硬阈值函数为

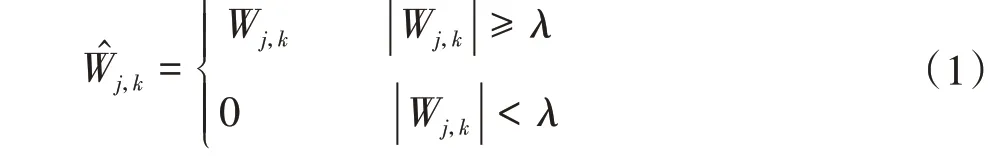
软阈值函数为

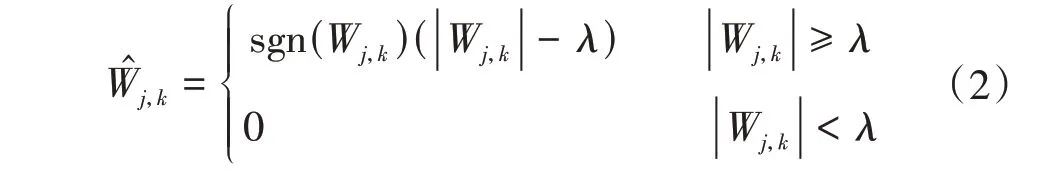
式中，Wj,k为小波系数；̂j,k为近似小波系数；λ为阈值，取，N为信号的长度。

1.2 双树复小波

图1所示为单层双树复小波中二叉树结构对信号的分解与重构，其主要由两个上下平行通道的离散小波变换构成，每个通道由两个不同的滤波器组成，将其分别称为实数部和虚数部。通过将虚数部的采样放置在实数部的中央位置，可以实现信息的互补性和近似平移不变性，更多地保留信号中的有效信息。双树复小波在振动信号各层分解过程中借用小波系数中的二分法，可进一步提高计算的速度。

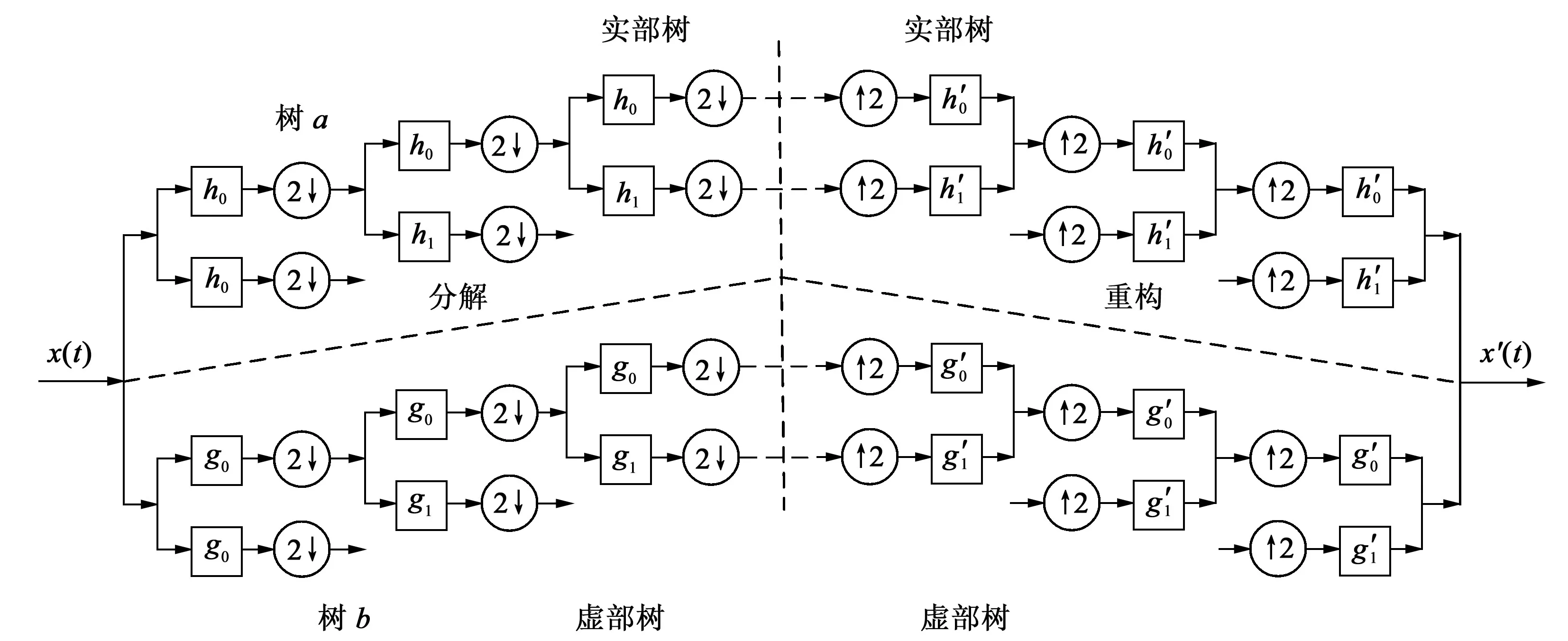
图1 双树复小波的分解与重构Fig.1 Decomposition and reconstruction of the double-tree complex wavelet

根据小波变换理论，一维复小波可以表示为式中，φh(t)、φg(t)分别为两个正交或双正交的实小波；i为虚数单位。

一维复小波实数部的小波系数和尺度系数分别为

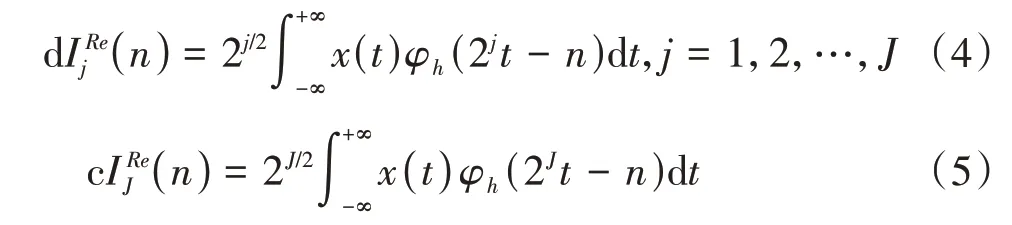
式中，j为层数；J为最大尺度；x(t)为带噪时间序列的振动信号。

同理，虚数部的小波系数和尺度系数分别为

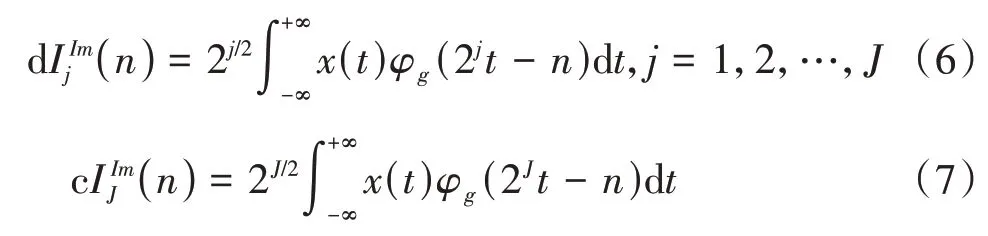
双树复小波变换由两个小波变换组成，则双树复小波的小波系数和尺度系数分别为

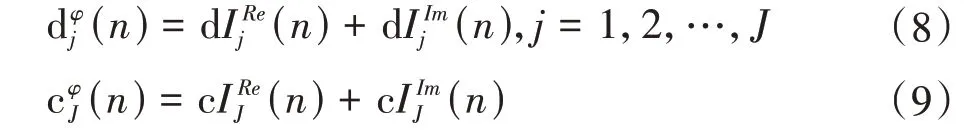
将双树复小波的小波系数和尺度系数进行重构，即

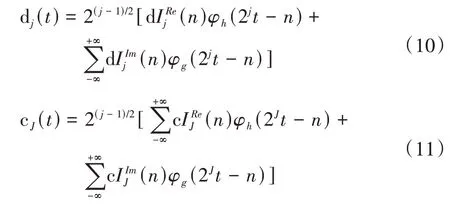
2 齿轮副振动信号的降噪

为获得齿轮箱原始的振动信号，使用图2所示的HD-CL-012C齿轮箱试验台进行实验。其中，齿轮副主要参数如表1 所示，电机转速设置为1 200 r/min，负载为48.8 N·m。

图2 齿轮箱试验台Fig.2 Test bench of gearboxs

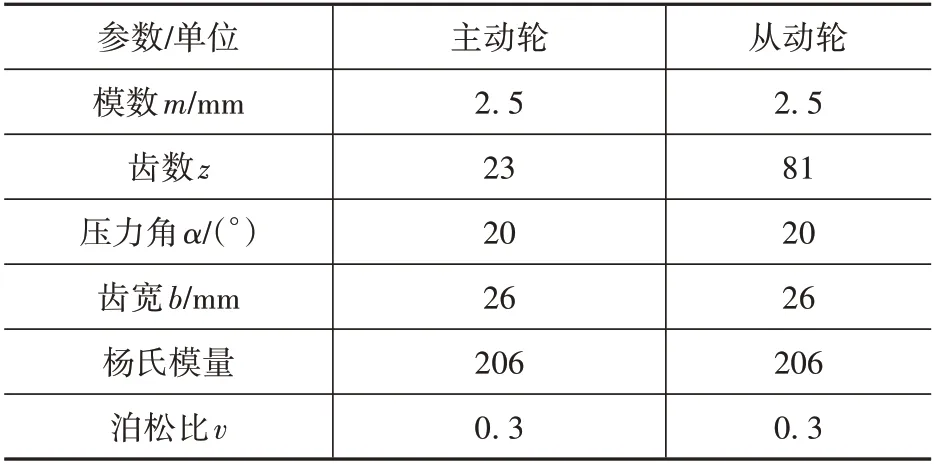
表1 齿轮副主要参数Tab.1 Main parameters of gear pair

利用三坐标加速度传感器采集齿轮箱的振动信号，选取高速齿轮一侧轴承端盖为测点，测量齿轮箱铅锤方向的加速度信号，该方向与齿轮副啮合线方向较为接近，所得到的振动加速度信号与齿轮副真实振动较为接近。数据采集系统的取样频率为10 kHz，进行测试后得到健康齿轮副振动原始信号，并通过快速傅里叶变换得到其频域响应，结果如图3所示。

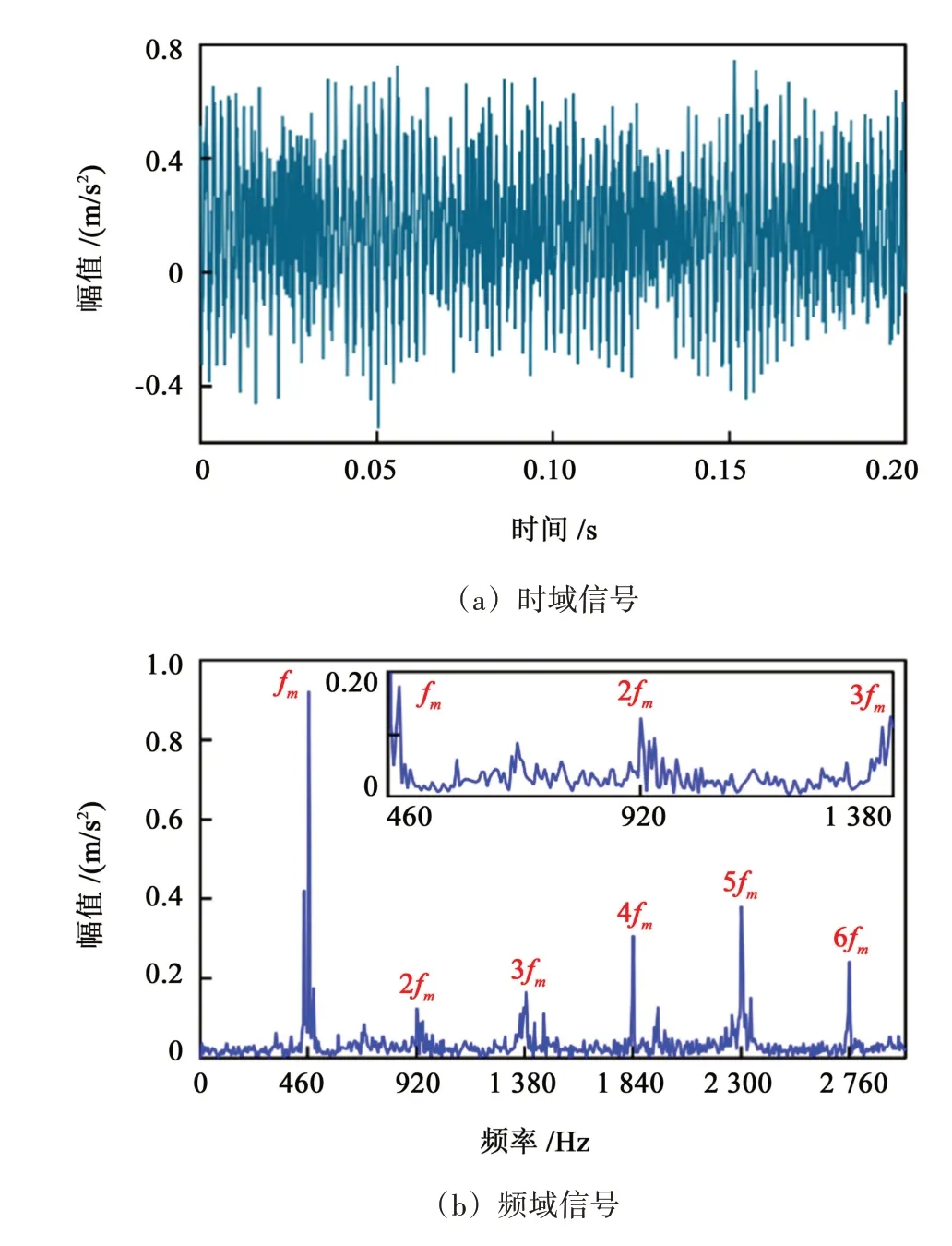
图3 实验测得健康齿轮副振动信号Fig.3 Vibration signalw of the gear pair measured by experiment

图3 所示为实验所得健康齿轮副振动信号。在图3（a）振动时域中，其振动幅值较为平均，没有明显周期性的脉冲冲击。在图3（b）振动频域中，其频谱组成主要为啮合频率及啮合频率高倍频（fm，2fm，3fm，…），频谱上存在锯齿状的杂频带，但相邻频带的间隔难以确定，这对齿轮副的健康状态判断带来很大难度。造成杂频带出现的原因很多，其中主要有：①齿轮副的制造安装误差，若齿轮副中存在一个或者多个零件出现制造安装误差，其误差会反映在振动信号中，造成振动信号中出现严重的频率调制现象；②齿轮副出现随机振动，环境噪声因素以及其他不利因素的白噪声的存在，使得三坐标加速度传感器在收集信号时出现杂频。从图3（b）中可以看出，齿轮副存在较严重的随机振动和白噪声成分，使得振动频域图上出现分布不均匀不规律的小幅值杂频，不利于对齿轮副健康状态的评估。

2.1 小波阈值滤波降噪

利用硬阈值函数和软阈值函数滤波降噪算法，处理如图3所示实验所得齿轮副振动原始信号，可得到硬阈值函数降噪的结果和软阈值函数降噪的结果，分别如图4、图5所示。

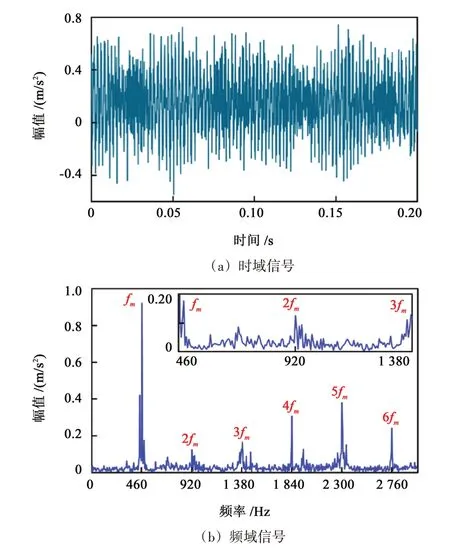
图4 硬阈值滤波降噪Fig.4 Hard threshold function filtering and noise reduction

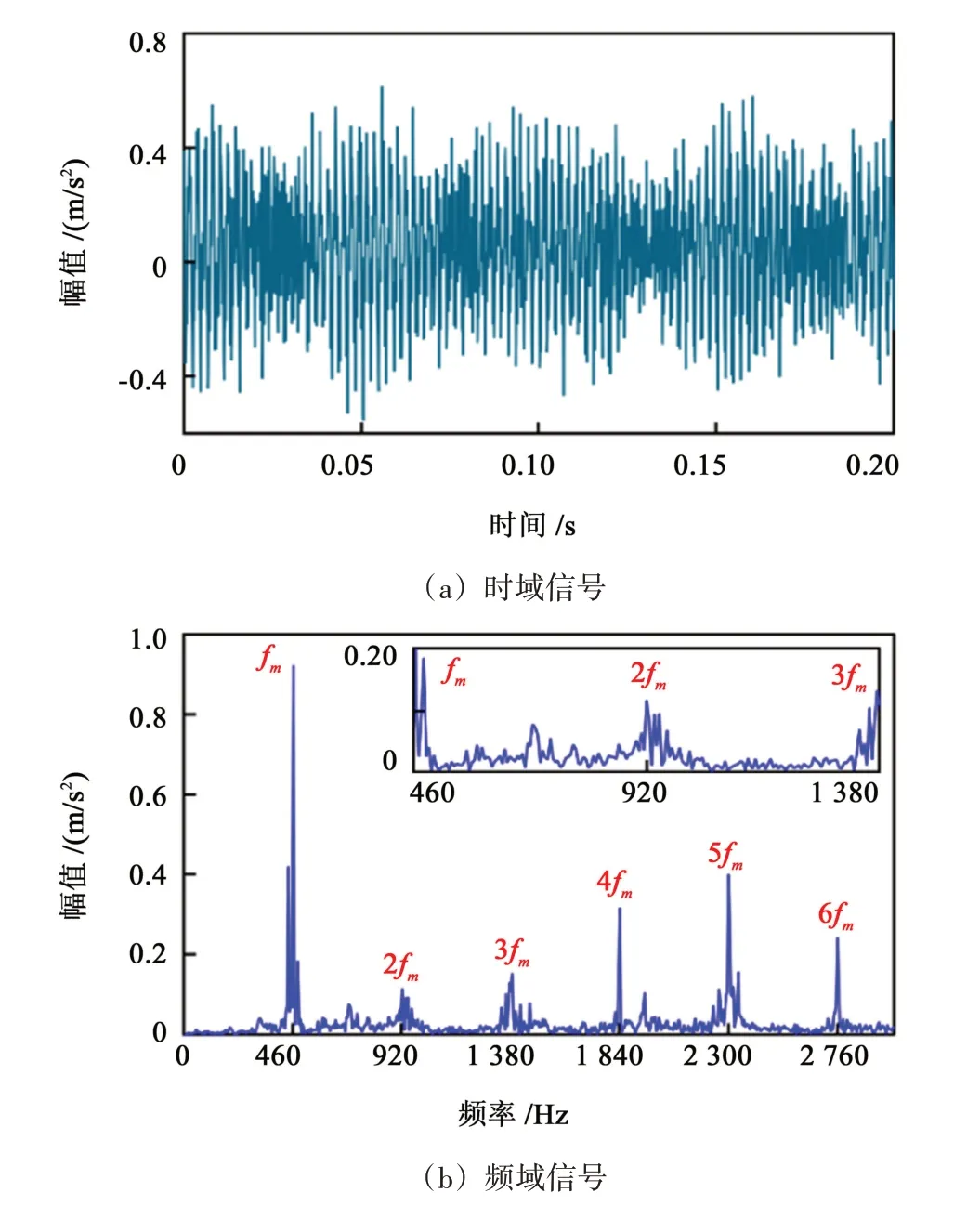
图5 软阈值滤波降噪Fig.5 Soft threshold function filtering and noise reduction

由图4、图5 中可知，采用传统的硬阈值函数、软阈值函数降噪处理，其降噪效果是一定的。降噪后的振动时域信号幅值分布稍稍平缓，无明显脉冲冲击；振动频域主要为啮合频率以及啮合频率的高倍谐波，边频带幅值减小。说明使用传统的小波阈值降噪能够减小信号中的噪声，但噪声频率和谐波频率同时被抑制，缺少对特征信号的识别能力，仍然难以分辨相邻边频带的频率间隔与主要分布区间。

2.2 4层双树复小波降噪

利用4层双树复小波对齿轮副振动信号进行降噪处理，得到处理后的齿轮副振动信号如图6所示。

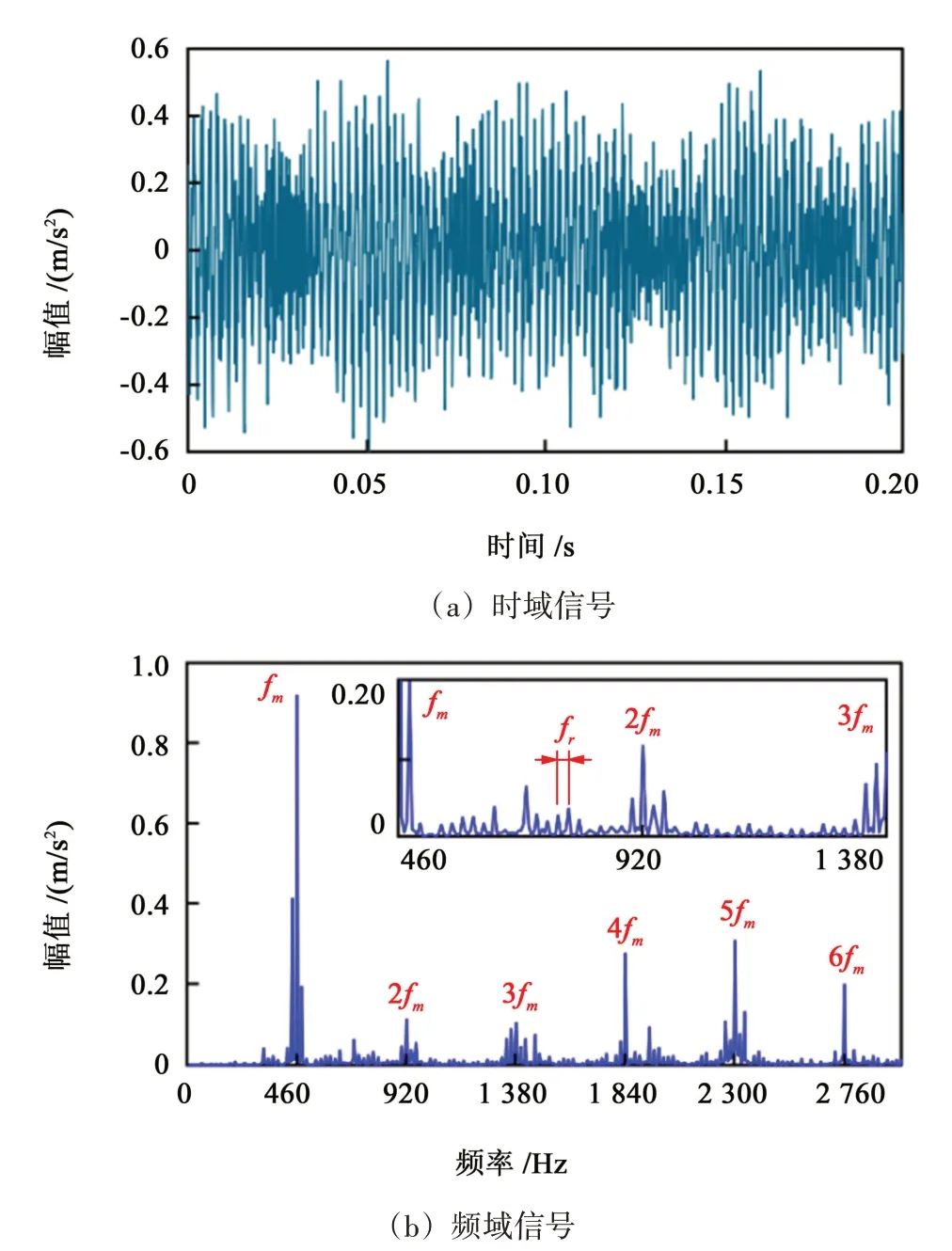
图6 双树复小波降噪Fig.6 Double-tree complex wavelet noise reduction

由图6 中可知，利用4 层双树复小波降噪后所得到的齿轮副振动信号较为理想，进一步说明了双树复小波对信号降噪的有效性。图6（a）所示健康齿轮副的振动时域幅值分布较为均匀，无明显周期性的脉冲冲击，齿轮副健康状态良好。图6（b）所示振动频域频谱主要组成仍为啮合频率以及倍频，此外，还存在分布规律的少量边频带，相邻边频带的频率间隔为转轴频率fr，说明健康齿轮副仍存在轻微的故障；但是，噪声因素造成的锯齿状杂频被有效过滤，降噪效果理想。这些频率间隔为转轴频率的边频带，可能是因为齿轮副安装不对中、动静平衡失效和齿轮的制造安装误差等因素所引起，但从边频带的幅值与分布区间可以看出，齿轮副整体上健康良好，无较大故障存在。

从图6中可知，双树复小波不但可以对信号进行有效降噪，减小振动时域信号中的间断现象，过滤掉振动频谱中噪声信号导致的杂频，还能够对故障信息进行有效识别，保留信号中的有效信息。

由图4、图5和图6中可以看出，3种降噪方法都可以通过信号分解和重构对齿轮箱振动信号进行降噪，减小信号中的部分噪声因素。为定量验证双树复小波变换在降噪效果上优于小波变换，求取降噪后信号的信噪比（Siangd-noise ratio，SNR）和均方根误差（Root mean square error，RMSE）进行比较，具体公式为

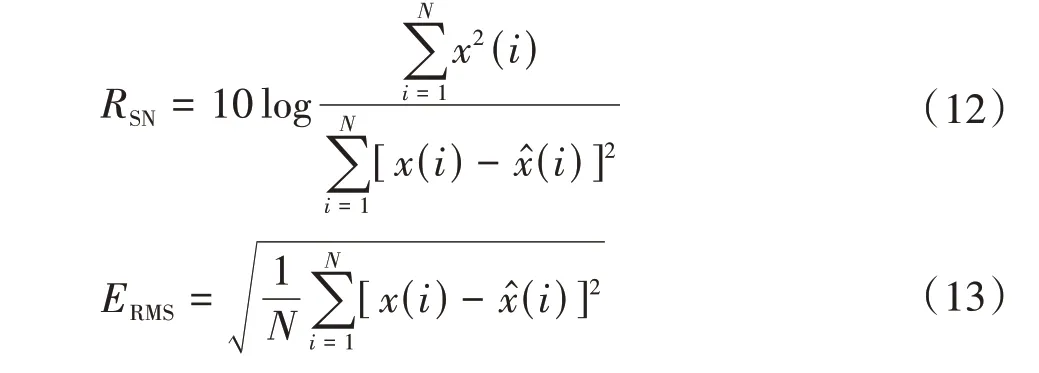
式中，x(i)为原始振动信号在第i点处的振动幅值；x̂(i)为降噪后信号在第i点处的振动幅值。将降噪信号与原始含噪信号的信噪比（SNR）和均方根误差（RMSE）作比较，结果如表2所示。

表2 降噪对比Tab.2 Noise reduction comparison

由表2中可以明显看出，通过小波变换和双树复小波变换对含噪信号进行降噪处理后，双树复小波的信噪比要明显高于硬阈值函数小波降噪和软阈值小波降噪，并且均方根误差皆小于两者，进一步说明双树复小波的降噪处理效果要比小波变换的效果好，因此，可以选用双树复小波变换方法对齿轮箱含噪信号进行降噪处理。

3 裂纹故障齿轮副振动实验

选取带有裂纹故障的主动齿轮如图7所示。其直线裂纹的深度为0.5 mm，裂纹方向与轮齿中心线夹角为70°。利用该故障件与健康低速齿轮相啮合，利用图2 所示的HD-CL-012C 齿轮箱试验台进行测试，同样利用三坐标加速度传感器采集齿轮箱振动信号，得到的原始振动信号如图8所示。进行双树复小波变换以完成降噪处理，再对降噪后的振动时域信号进行快速傅里叶变换得到其振动频谱，结果如图9所示。

图7 裂纹故障高速齿轮Fig.7 High-speed gears with crack defects

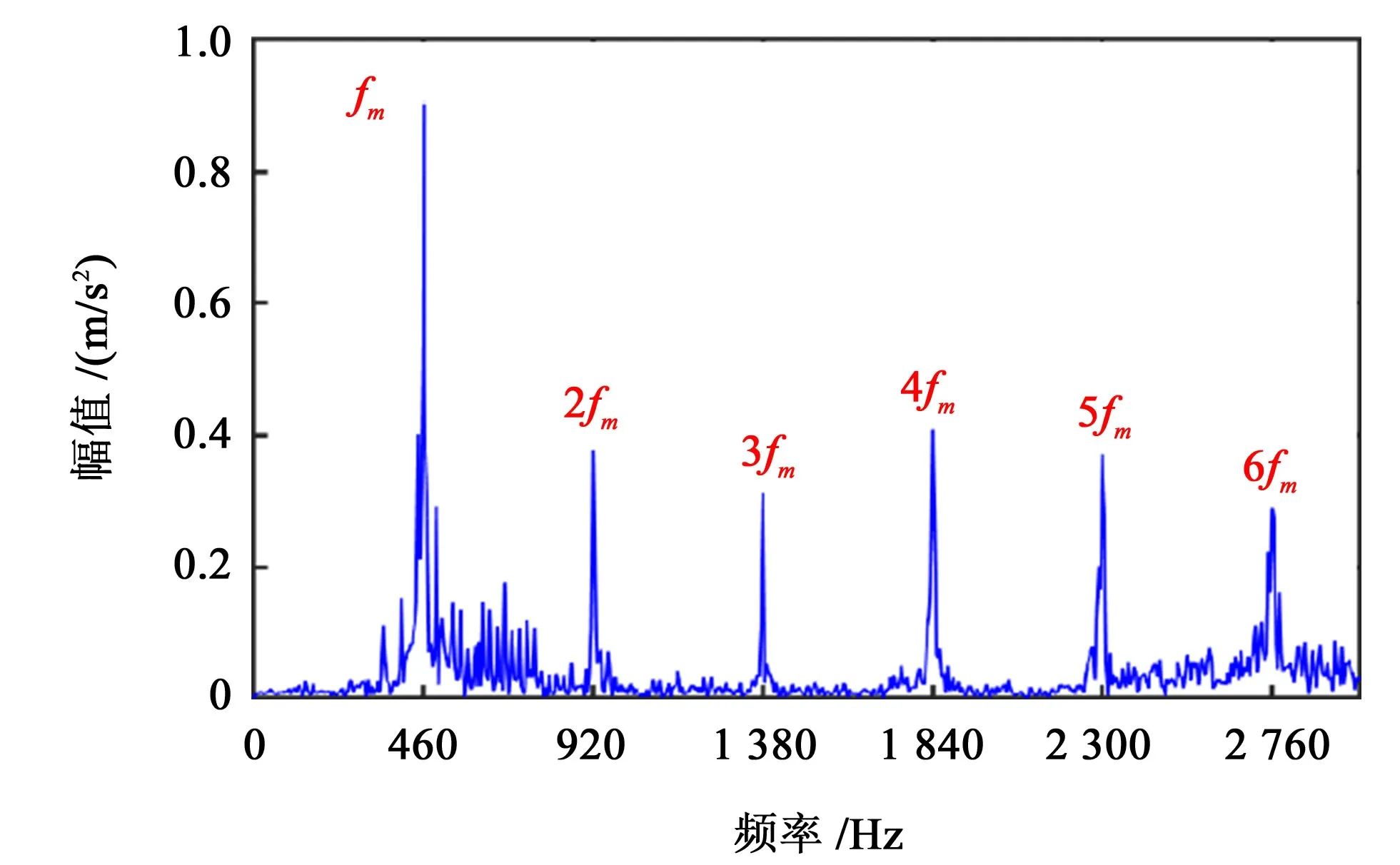
图8 裂纹故障齿轮副振动含噪信号Fig.8 Vibration signals before noise reduction of the gear pair with crack defects

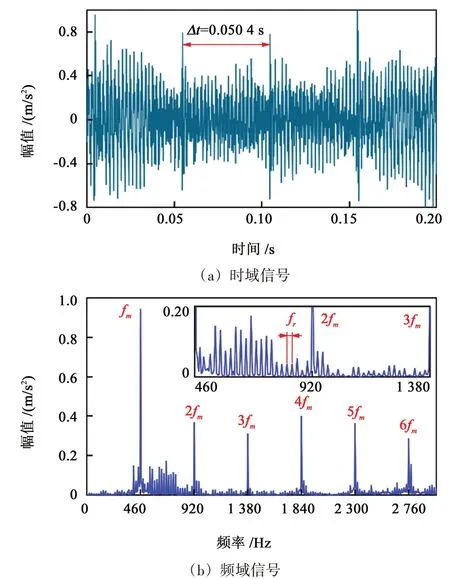
图9 降噪后裂纹齿轮副振动信号Fig.9 Vibration signals after noise reduction of the gear pair with crack defects

由图8中可知，齿轮副含噪振动频域信号的频谱组成为齿轮副的啮合频率以及高倍谐波。但是，频谱中也存在小幅值锯齿状的噪声信号，这对齿轮副的谐波频率识别带来极大困难。由图9中可知，在裂纹齿轮副振动时域上，存在明显的周期性脉冲冲击，相邻冲击的时间间隔为0.050 4 s，与高速齿轮转频相一致，可以判定齿轮副局部故障发生在小齿轮上。同时从频域上分析，其频谱组成主要为齿轮副啮合频率及谐波，存在调制生成的边频带，相邻边频带间隔明显，为转轴频率fr，而且边频带分布主要位于啮合频率的2 倍频到3 倍频，以及6 倍频左右，啮合频率的3倍频4倍频之间的边频带分别较少。

实验结果说明，利用双树复小波变换降噪后的信号特征明显，能够准确快速监测齿轮副的健康状态，避免了噪声因素引起杂频带而导致的错误判别。

4 结论

针对裂纹故障齿轮副振动信号的降噪问题，利用双树复小波变换对振动信号进行降噪处理，利用信号的分解与重构完成对信号的处理，并与传统的小波变换降噪方法进行对比实验，比较了不同方法的降噪效果。得到如下结论：

小波变换和双树复小波变换都能对齿轮副含噪振动信号进行降噪处理，但双树复小波变换降噪效果明显优于小波变换，其降噪后信号的信噪比高，均方根误差小。在双树复小波降噪过程中，不但能够有效过滤噪声因素，而且能够保留信号中的特征信息。