成捆棒材贴标机器人系统部件空间位置优化

张付祥 郑 雨 黄永建 王春梅 黄风山

（1 河北科技大学 机械工程学院， 河北 石家庄 050018）

（2 石家庄钢铁有限责任公司， 河北 石家庄 050031）

（3 河北科技大学 电气工程学院， 河北 石家庄 050018）

0 引言

目前，国内钢厂棒材精整线信息追溯的方式还是由人工在棒材端面粘贴生产信息标签。随着“工业4.0”的提出，制造技术正在向智能化方向发展。在保证贴标效率的前提下，利用成捆棒材端面贴标机器人系统实现钢厂棒材信息追溯是一个亟待解决的问题。

自动贴标机发展非常迅速且用途广泛[1-2]。魏会芳等[3]提出通过机械手系统实现钢卷自动贴标；金玉阳等[4]提出了以单片机和PC 机为核心的行李自动贴标控制系统。已有贴标机在待贴工件位置相对固定环境下的应用效果良好，但面对钢厂成捆棒材端面位置不确定的环境却很难实现。贴标机各部件之间的位置关系十分重要，如果摆放位置不合理，会影响工作效率及质量，需要进行空间位置优化[5]。张付祥等[6]提出成捆钢筋端面自动贴标系统，并采用标准的粒子群优化算法对机器人的摆放位置进行了优化。

本文中根据钢厂现场环境建立成捆棒材贴标机器人系统。贴标时，由于工业机器人和标签打印机的空间位置将影响机器人工作路径和贴标效率，因此，以机器人贴标过程中的关节转角总行程最短作为工业机器人和标签打印机空间摆放位置的优化目标，对工业机器人进行运动学分析，求取其正运动学与逆运动学解析解，利用蒙特卡洛法生成棒材端面的中心空间坐标，采用改进的粒子群优化算法以实现工业机器人和标签打印机的空间位置优化。

1 成捆棒材贴标机器人系统

成捆棒材贴标机器人系统如图1所示，包括供压单元、控制单元、视觉单元、标签打印机和工业机器人。贴标机器人系统放置在棒材精整线的称重工位，成捆棒材端面最大不平齐度为20 mm，工业机器人末端操作器最大压缩行程为50 mm。工业机器人和标签打印机摆放位置将直接影响贴标机器人系统的贴标效率。对工业机器人进行运动学分析，建立用户坐标系、工业机器人坐标系和标签打印机坐标系；在此基础上，求解工业机器人和标签打印机的最佳空间摆放位置。

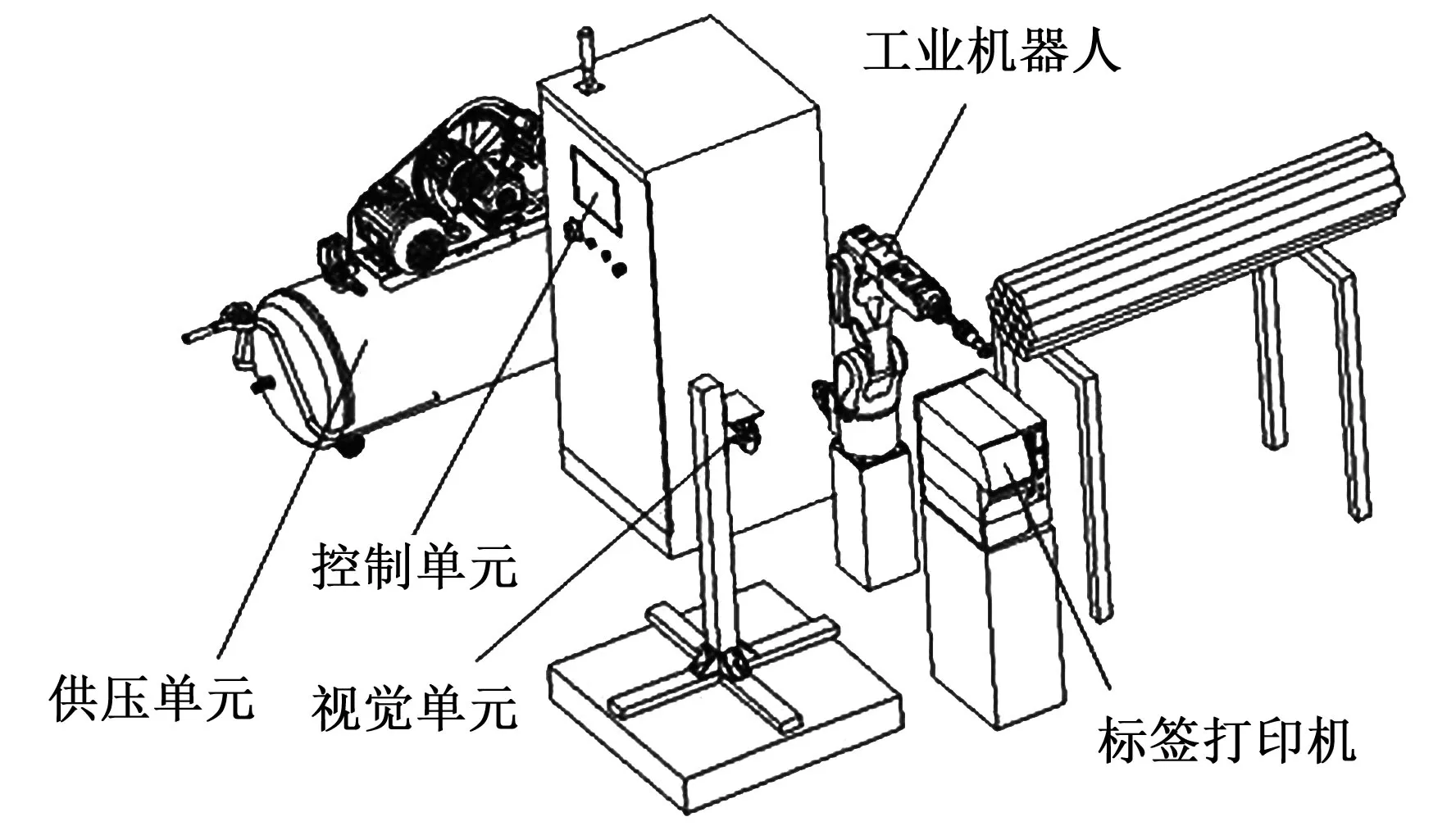
图1 贴标机器人系统Fig.1 Labeling robot system

贴标机器人系统坐标系如图2所示。贴标机器人系统的标签打印机选用斑马公司的ZT410 型打印剥离一体工业打印机，工业机器人选用埃夫特公司的ER7L-C10 型6 自由度工业机器人。以成捆棒材整体端面的理论平面作为Xw-Yw平面。由于一捆棒材最大直径不超过360 mm，成捆棒材支架水平放置，以成捆棒材最大直径中心为原点Ow，以水平向右为Xw正方向，以竖直向上为Yw正方向，建立用户坐标系。以工业机器人固定底座法兰盘中心为原点O0，工业机器人坐标系的X0轴与用户坐标系的Xw轴方向一致，工业机器人坐标系的Z0轴与用户坐标系的Yw轴方向一致，建立工业机器人坐标系。以标签打印机打印的标签中心点为原点OP，标签打印机坐标系的XP轴与工业机器人坐标系的X0轴方向一致，标签打印机坐标系的ZP轴与工业机器人坐标系的Z0轴方向一致。

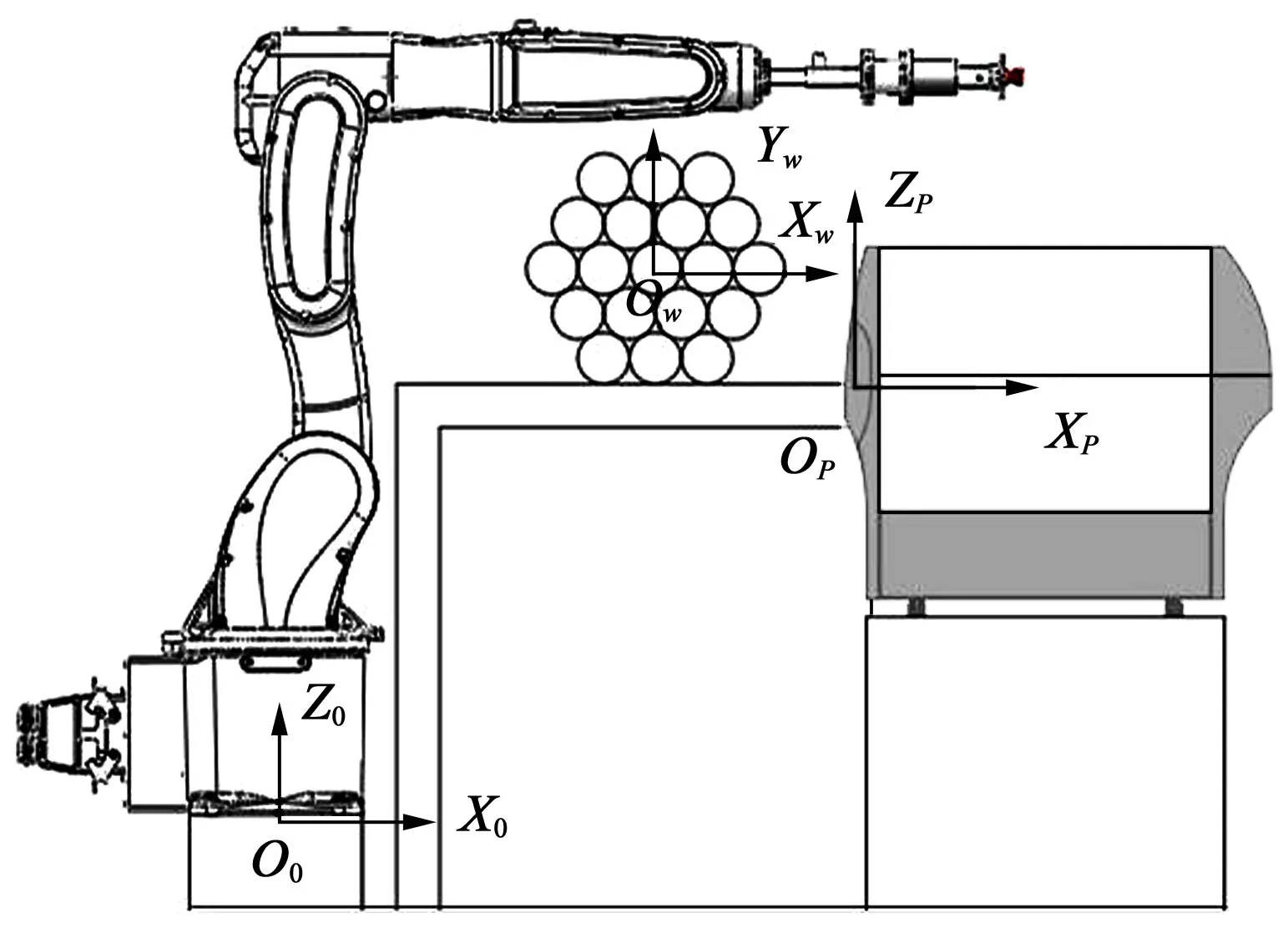
图2 贴标机器人系统坐标系Fig.2 Coordinate systems of the labeling robot system

2 工业机器人运动学分析

2.1 ER7L-C10机器人运动学正解

根据ER7L-C10机器人厂家提供的机器人连杆信息，确定其机器人D-H参数如表1所示。

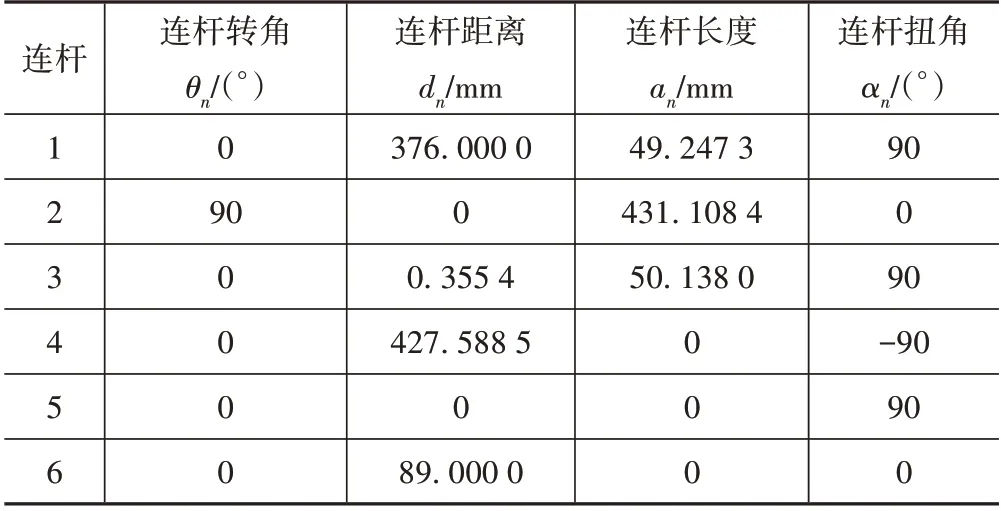
表1 机器人D-H参数Tab.1 D-H parameters of the robot

标准D-H 参数法[7]的ER7L-C10 工业机器人相邻两个坐标系之间的齐次变换矩阵通式An为

为简化三角函数符号，下文中以sn表示sinθn；cn表示cosθn；s23表示sin（θ2+θ3）；c23表示cos（θ2+θ3）。根据D-H参数，求得A1～A6变换矩阵为

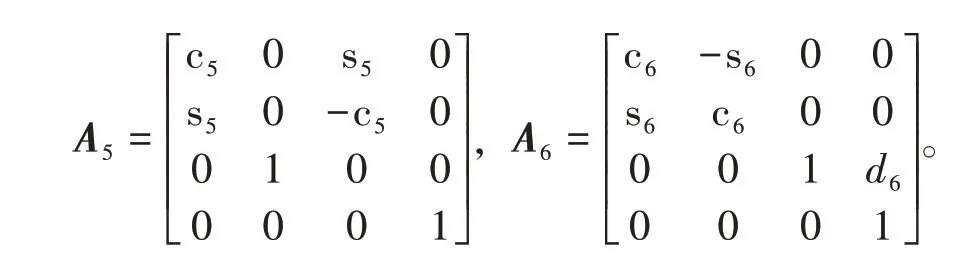
将齐次变换矩阵A1-A6连乘，得到ER7L-C10 工业机器人从基座到TCP的齐次变换矩阵T6为

2.2 ER7L-C10机器人运动学反解

应用解析法[8]中的分离变量法[9]实现机器人逆运动学的解析解求解，根据“最小行程法”规则实现逆解选解[10]。根据机器人ER7L-C10 的结构特性，关节5角度为0°时，机器人处于奇异点，需要判断θ4和θ6解的情况。

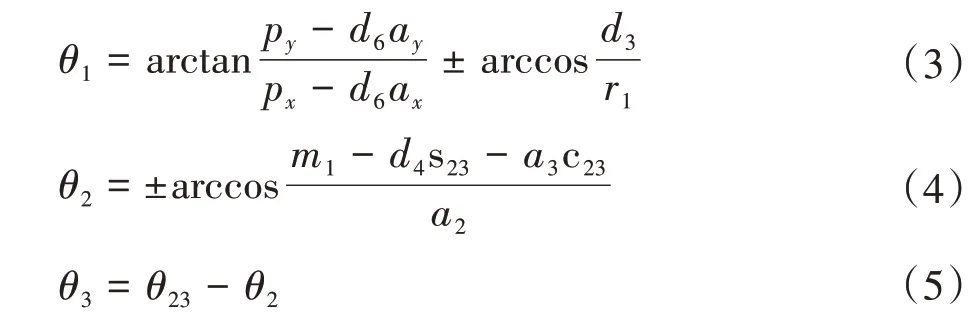
求解关节角θ1、θ2、θ3关节角分别为当关节角θ5≠0时，求解θ4、θ5、θ6关节角分别为

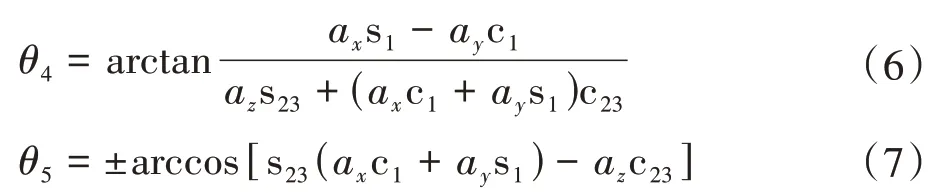
当关节角θ5=0 时，求解θ46关节角，通过给定θ4或θ6关节角值，实现θ4和θ6解析解求解，为

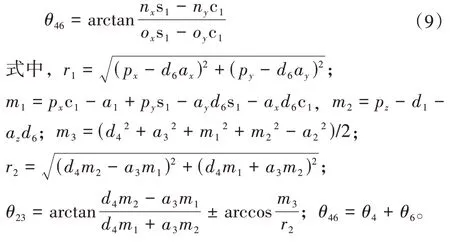
3 空间位置优化的数学模型

3.1 工业机器人和打印机的空间位置约束条件

贴标机器人系统中，视觉单元布置在棒材正前方。为了避免遮挡相机视野，将工业机器人摆放在棒材的侧面。这里将工业机器人放置在棒材左侧，标签打印机放置在工业机器人右侧。工业机器人的末端操作器长为300 mm、压缩总行程为50 mm。为了保证设备安全，在用户坐标系Zw轴为340 mm 处，ER7L-C10工业机器人通过直线运动贴标，末端操作器压缩行程为40 mm，贴标时工业机器人直线运动距离为80 mm。ER7L-C10 工业机器人最大工作半径为910 mm，为了保证成捆棒材和标签打印机在机器人的工作空间内，综合考虑工业机器人结构和工作方式，限定工业机器人摆放位置在用户坐标系下的范围为-620 mm＜x1＜-200 mm， -640 mm＜y1＜-200 mm，200 mm＜z1＜700 mm；标签打印机的摆放位置在工业机器人坐标系下的范围为600 mm＜x2＜1 000 mm，-400 mm＜y2＜400 mm，0 mm＜z2＜600 mm。

工业机器人贴标时，工具坐标系的Z轴垂直棒材端面；机器人取标时，工具坐标系的Z轴垂直标签表面。根据单根棒材中心坐标Pb=[xb yb zb]T，通过试验确定机器人运动到贴标位置的机器人世界坐标位姿矩阵TP为

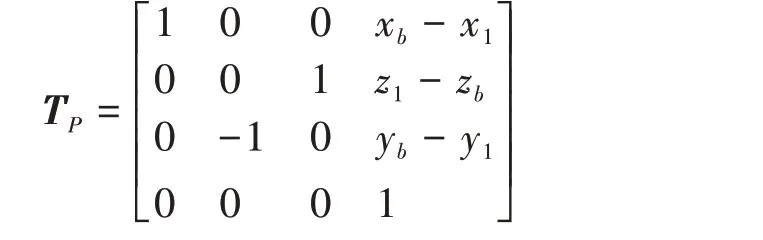
取标位置的机器人世界坐标位姿矩阵Tt为

3.2 成捆棒材端面中心坐标

工业现场成捆棒材端面最大不平齐度为20 mm，最大捆直径为360 mm，棒材直径范围为50 mm～200 mm，棒材中心坐标在用户坐标系下的范围为：-160 mm＜xb＜160 mm，-160 mm＜yb＜160 mm，-20 mm＜zb＜0 mm。为了保证工业机器人和标签打印机摆放位置固定后贴标位置在工业机器人工作范围内，应用蒙特卡洛法随机产生2 000 个空间点，模拟棒材中心坐标。

3.3 优化设计的数学模型

空间位置优化设计的基本思想是遵循成捆棒材贴标时机器人各关节转角总行程最小原则。利用工业机器人逆运动学解析解表达式，将取标位置和所有贴标位置的世界坐标位姿矩阵转化为机器人关节坐标，计算出机器人从取标位置运动到贴标位置的各关节转角改变量；对各关节转角改变量取绝对值求和，即为每根棒材的关节转角总行程；工业机器人的关节转角总行程为成捆棒材中每根棒材关节转角总行程的和。优化设计就是利用优化算法求解工业机器人的关节转角总行程的最小值。优化设计的数学模型为

式中，f为所有粒子最小适应度值；N为一捆棒材根数；θ1j为贴标位置各关节转角；θ2j为取标位置各关节转角；j=1，2，…，6；i=1，2，…，N。

4 优化计算

4.1 改进的粒子群优化算法

传统粒子群优化算法具有运算简单、收敛快、参数少等优点，但面对复杂函数时存在易陷入局部最优、搜索精度不高等现象[11-12]，原因在于惯性权重、粒子数、学习因子等控制参数的选择极大地影响着粒子群算法的性能[13-15]。在粒子群优化中，粒子的速度和位置通过对比粒子的个体最优值和全局最优值实现更新，有

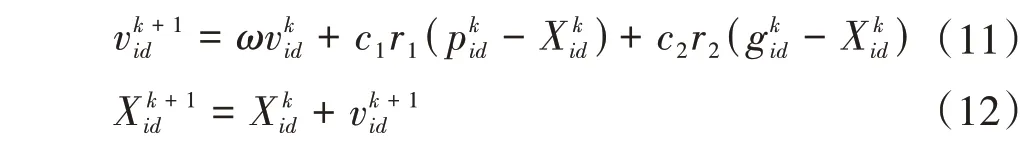
本文中对粒子群算法各参数改进如下：

（1）非线性动态调节惯性权重惯性权重ω的大小影响粒子群算法的全局或者局部搜索能力，固定的惯性权重容易陷入局部最优。为了提高算法在迭代初期的全局搜索能力，增强迭代后期局部搜索能力，利用非线性递减的惯性权重系数，平衡算法的搜索能力[16-18]。基于Tanh 函数提出非线性变化的惯性权重计算公式为

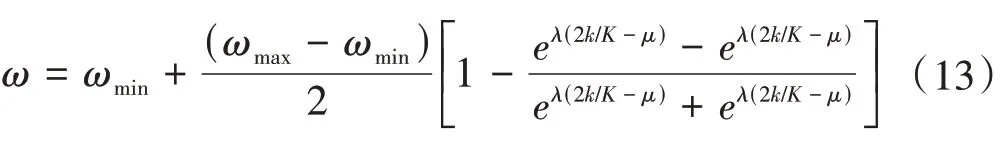
式中，ωmin、ωmax分别为惯性权重的最小值和最大值；K为迭代总数；λ为放大系数；μ为平移系数。

（2）异步变化学习因子调节

采用动态变化的学习因子提高算法计算效率，避免算法计算结果陷入局部最优。在算法优化的前期，应用较大的个体学习因子和较小的社会学习因子；在算法优化的后期，应用较小的个体学习因子和较大的社会学习因子[19-20]。将三角函数引入异步非线性变化的学习因子，有

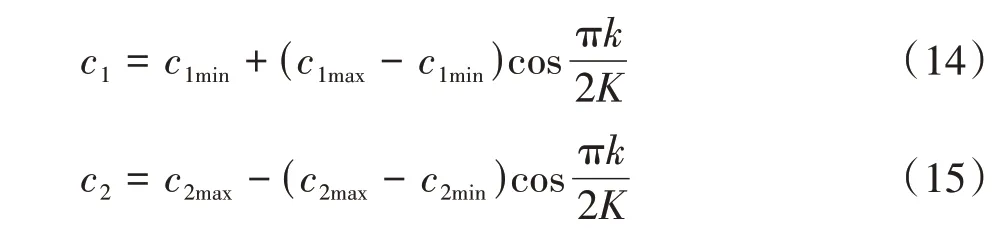
式中，c1max、c1min分别为最大和最小个体学习因子；c2max、c2min分别为最大和最小社会学习因子。

（3）非线性递减的粒子数目

工业机器人和标签打印机的空间位置优化采用传统的粒子群算法耗时较长，原因是采用蒙特卡洛法随机生成的2 000 根棒材需要较大的粒子数目实现粒子群迭代求解，每次迭代的粒子数目保持不变会导致较长时间的迭代计算[21]。因此，提出将粒子数目非线性递减，有

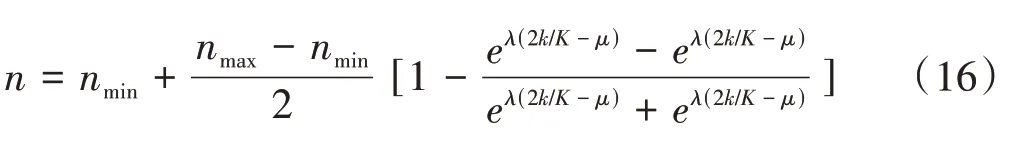
式中，nmax为迭代最大粒子数；nmin为迭代最小粒子数。

本文中提出的改进粒子群优化算法简称IPSO，IPSO算法通过式（13）～式（16）实现惯性权重、学习因子和粒子数目的更新。求解工业机器人和标签打印机最优空间位置的IPSO算法流程如图3所示。

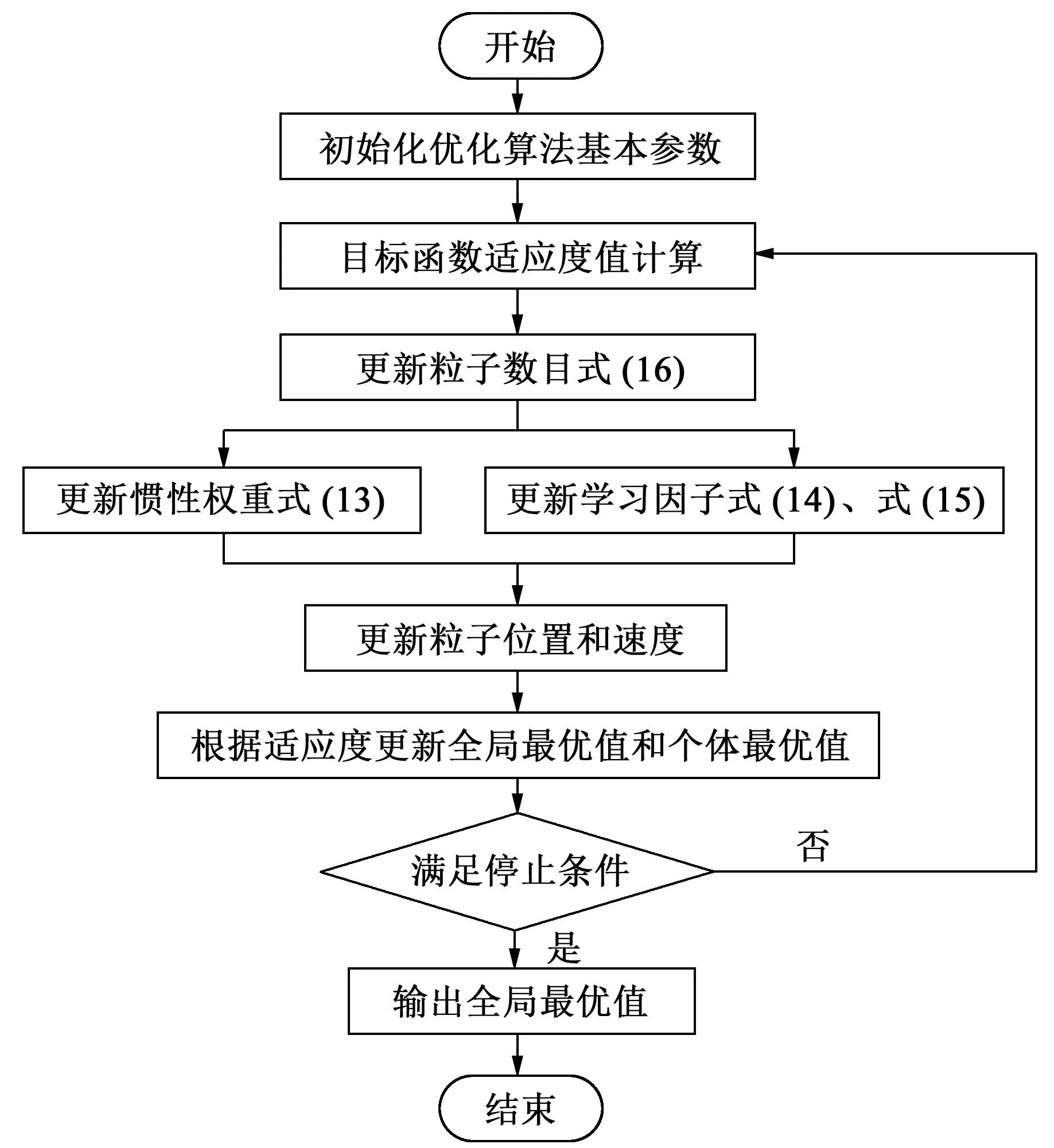
图3 IPSO算法流程图Fig.3 IPSO algorithm flow chart

4.2 优化计算及结果分析

采用IPSO 算法，基于蒙特卡洛法随机产生棒材中心坐标，实现工业机器人和标签打印机空间位置优化。

迭代总数K= 200，计算参数：式（13）中的参数，λ= 8，μ= 1，ωmin= 0.4，ωmax= 0.8；式（14）中的参数，c1min= 0.5，c1max= 2.5；式（15）中的参数c2min= 0.5，c2max= 2.5；式（16）中的参数，nmax= 150，nmin= 50，μ= 1.1。

IPSO 算法与PSO 算法的迭代次数与适应度关系曲线如图4 所示。最优适应度和迭代时间如表2所示。

根据图4 和表2 中IPSO 算法和PSO 算法的对比结果可以看出，IPSO 算法适应度收敛精度更高，并且迭代时间减少14.87%，这是由于IPSO 算法采用非线性变化的惯性权重、学习因子和粒子数目，在保证算法的全局搜索能力的同时，减少了算法迭代后期的粒子数目，因此，其迭代速度和全局寻优能力都有一定程度的加强。

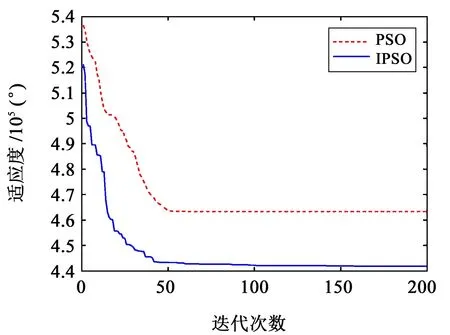
图4 目标函数迭代收敛图Fig.4 Iterative convergence graph of objective function

表2 最优适应度和迭代时间Tab.2 Optimal fitness and iteration time

采用经验法、PSO 算法和IPSO 算法的工业机器人和标签打印机的空间坐标如表3所示。根据上述蒙特卡洛法随机生成2 000 根棒材中心坐标和工业机器人、标签打印机空间坐标，计算贴标机器人贴标过程关节转角总行程。依据表3中3种算法的对比结果可知，采用IPSO 算法计算出的工业机器人和标签打印机的空间位置在贴标过程中的关节转角总行程最小，贴标效率最高。

表3 贴标机器人系统各部件空间坐标Tab.3 Spatial coordinates of components of labeling robot system

5 结论

（1）以成捆棒材贴标机器人系统部件的空间位置为研究对象，提出改进的粒子群优化算法，实现了工业机器人和标签打印机空间位置优化。实验结果表明，提出的IPSO 算法相对标准PSO 算法具有更高的收敛精度和优化效率。

（2）采用D-H 参数法，对成捆棒材贴标机器人系统中的ER7L-C10工业机器人进行运动学分析，实现其正运动学和逆运动学解析解的求解，确定了贴标和取标的位姿矩阵。

（3）以贴标机器人系统贴标过程中各关节转角总行程最小为优化目标，采用改进的粒子群优化算法对目标函数进行优化，得到工业机器人和标签打印机最佳空间摆放位置，提高了贴标机器人系统的工作效率，为贴标机器人系统建立时各部件摆放的空间位置提供理论指导。