波纹度误差对滚动轴承振动特性的影响

田富文

（重庆交通大学 机电与车辆工程学院，重庆 400074）

因滚动轴承有着轴向体积小，摩擦力矩小，启动所需力矩小等优点，被广泛应用于航天航空、汽车变速箱、矿山机械、蒸汽轮机等众多设备的支撑零部件。滚动轴承作为支撑回转的重要零部件，其运行精度和可靠性对整个传动系统的安全和效率起着决定性作用。在航天航空领域，滚动轴承一旦有微小振动或其他故障就会导致飞行的的不稳定，甚至会造成机毁人亡重大事故。

Zhang等[1]在考虑滚动体局部故障和内外圈矩形故障的耦合情况下，建立了滚动轴承的4自由度的动力学模型，研究了径向载荷、轴的转速、故障尺寸对轴承的动态响应的影响；Patil[2]在考虑了内外圈局部故障的情况下，建立了轴承内圈2自由度的振动方程，研究了缺陷尺寸和缺陷的初始相位对轴承振动的影响；Shi[3]考虑了保持架和滚动体的非线性接触力和摩擦力以及油膜厚度，建立了包括滚动体、保持架、内外圈在内的11自由度的动力学模型，研究了轴承的径向间隙、输入轴转速、径向载荷对轴承振动的影响；Liu[4]考虑了矩形故障引起的尖峰并引入故障函数来表示故障类型，用分段函数表示时变接触刚度，建立了关于内外圈的动力学微分方程，并求解了其动态响应。余光伟[5]以深沟球为研究对象，建立了考虑表面波纹度误差的轴承动力学模型，并分析了不同转速下的轴承的动态响应；徐东[6]建立了单表面故障的轴承动力学模型，并考虑了非线性接触力，最后求解了轴承的动态响应。Zhang[1]建立了滚动轴承5自由度的动力学模型，考虑了5种不同矩形故障缺陷对轴承的动态响应的影响，最后通过实验证明了提出的故障模型的正确性。

通过上述文献可以看出，滚动轴承的研究内容主要是考虑其故障对动态特性的影响，故障主要分为局部故障和分布式故障；局部故障一般处理为一个矩形缺口，通过引入分段函数来模拟轴承通过故障时所引起的位移的变化[7]；而分布式故障又包括圆度误差和波纹度误差，圆度和波纹度是由于制造和加工误差分别引起的轴承圆度的不规整和轴承表面的不光滑[8]。这两种现象受加工精度的影响和人为因素的影响，是不可避免的，会对轴承的动态响应和振动特性产生影响。由于对这方面的研究较少，因此，综合考虑了轴承内外圈的表面波纹误差，建立了关于内外圈4自由度的动力学微分方程，研究了不同波纹幅值的变化、不同径向间隙变化对轴承振动响应的影响。

1 轴承故障模型

滚动轴承转作为支撑回转的精密性零件，其装配精度和制造精度会影响整个系统的响应。由于轴承在加工过程中，其内外圈滚道的表面粗糙度不可能是绝对光滑的，因此会导致轴承每次通过不光滑表面都会产生一次振动冲击；另外一种原因就是，轴承圆度受制造误差的影响，会导致轴承在运行过程中侧隙的不断改变，进而产生冲击。因此，为了考虑以上两种类型的冲击，模拟滚动轴承存在制造误差和装配精度误差的情况下，更好的反应真实条件下的轴承运转，建立了考虑轴承内外圈分布式故障的故障模型。其故障模型如图1所示。

图1 内外圈滚道波纹

滚动轴承作为精密的轴系支撑回转类零件，由于本身的材料属性和制造加工中所存在的误差，会使内外圈滚到产生微小的凸起或者凹陷，这种误差会使滚动体每次经过此缺陷所在的位置，都会产生一次冲击和额外的振动，如果此误差造成的冲击频率和其他支撑回转类零件的固有频率重合，将会产生共振，严重影响滚动轴承的运行，并且可能产生疲劳破坏。因此，为了探究滚动轴承表面波纹度对滚动轴承振动特性的影响，对滚动轴承表面波纹度进行建模。

具体波纹度的数值[6]参可见参考文献，表面波纹可以考虑为脉冲函数，在每个滚子接触到外圈上的波纹时候，都会引起轴承的间隙的改变，从而引起轴承的振动，其表达式可以写成：

式中：Aoi代表波纹的幅值，n代表波纹的总数，ωi为内圈的旋转角速度，ωc为保持架的旋转角速度，Z为滚动体个数，βli代表波纹的初始相位，j为滚动体。

根据上述内圈的波纹度表达式，可以类比推导出外圈波纹表达式可以写为：

式中：Aij代表波纹的幅值，n代表波纹的总数，ωo-ωc代表外圈相对于保持架的旋转频率，Z代表滚动轴承的总球数，βij代表波纹的初始相位，j表示为第几个滚动体。

对于第j个滚动体的位置可以计算为：

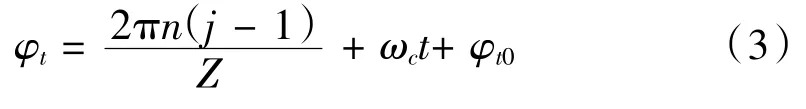
式中，ωc为保持架的旋转速度，φt0为第j个滚动体的初始相位角。

由于忽略了滚动体的离心力和陀螺力矩，根据滚动轴承的受力分析可以推导出滚动轴承的变形协调方程，取第j个滚动体为研究对象，因此第j个滚动体与内圈的接触变形可以表示为：

式中，γ表示轴承的初始间隙，P为轴承的表面波纹度误差和圆度误差函数。

因为滚动轴承在运动过程中会出现承载区和非承载区，当滚动体在非承载区的时候，是不会产生接触变形，因此此时的轴承的接触力也为零[9]，为了描述滚动轴承在承载区和非承载区的的变化，引入判断函数H（j）：当δj＞0，H（j）等于1；当δj≤0时，此时H（j）等于0。

根据赫兹接触理论可以求出滚动体与内外圈的接触力：

式中，K表示为变形系数，n为接触系数。

因此，可以得出滚动轴承在水平和垂直方向的非线性接触力：

2 轴承的动力学模型

本研究的轴承型号为深沟球轴承，并对其做出以下假设：

（1）滚动体在运动过程中只考虑滚动且忽略打滑现象。

（2）忽略保持架和滚动体在运动过程中的摩擦效应。

（3）将滚动体等效为弹簧和阻尼。

（4）忽略滚动体的质量。

根据参考文献[10]建立的滚动轴承动力学模型，为了研究滚动轴承的动力学特性，对滚动轴承外圈固定，内圈与输入轴相连接并做旋转运动，考虑内圈和外圈在x，y方向的振动，基于牛顿第二定律，建立关于轴承内圈和外圈的振动微分方程：

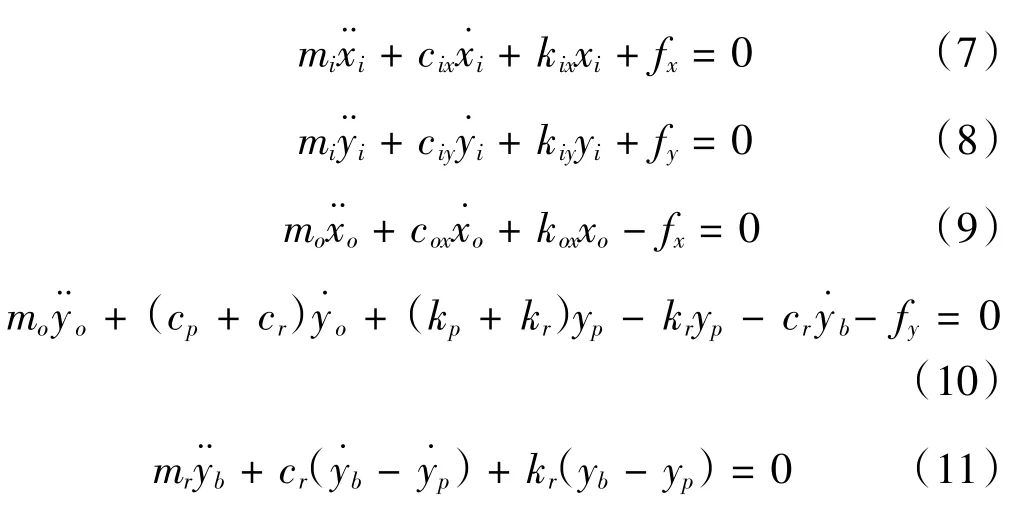
式中：xi，yi分别带代表轴承内圈和转轴在x，y方向的振动位移；xo，yo分别代表为轴承外圈和轴承座在x方向和y方向的振动位移；mi为轴承内圈和转轴的质量；mo为轴承外圈和轴承座的质量；mr为谐振器的质量；ci为转轴的阻尼；cp为轴承座的阻尼；cr为弹簧的阻尼；ki为转轴的支撑刚度；ko为轴承座的支撑刚度；kr为弹簧系统的刚度；fx和fy分别为轴承在x方向和y方向上的非线性支撑力。

轴承的详细参数见表1。

表1 深沟球轴承参数

3 结果与讨论

为了分析轴承的动态特性变化，基于上述的动力学方程，通过采用MATLAB中的定步长四阶龙格库塔法求解轴承的动态响应，内圈和转轴的总质量M为2 kg，外圈与轴承座的总质量为10 kg；阻尼为100 N·s/m；滚动体与内外圈的接触刚度为6.6×108n/m，轴承的输入转速为600 r/min，通过求解轴承运动的微分方程，可以得到轴承内外圈的振动位移。

为了和滚动轴承内外圈存在波纹度故障时的动态响应形成对比，先对滚动轴承进行无故障分析，取输入转速为600 r/min，从图2可以看出，当滚动轴承无故障时，轴承外圈的振动具有周期性变化，因为轴承的滚动体均匀地排列在保持架上，轴承各个滚动体的时变位置角也具有规律性。此时轴承外圈在x方向上的振动位移大小为1.2553×10-4m。

图2 无故障时滚动轴承x方向的振动位移

为了分析轴承加工误差和制造误差造成表面的不光滑特性和轴承圆度对轴承动力学响应的影响，分别引入波纹度函数来模拟误差，分别取波纹度幅值为10 μm来探究对轴承的动力学特性的影响，输入转速为600 r/min。

图3 波纹幅值为10 μmx方向的振动位移

当幅值为10 μm时，输入转速为600 r/min，轴承的振动位移如图（2）所示，此时轴承外圈在x方向振动位移的幅值4.86×10-4m，波纹度幅值通过影响轴承的接触变形进而影响轴承的接触力，在接触刚度确定的条件下，当总的接触变形增大，内圈的振动位移会增加，导致轴承的振动位移增大。通过以上分析表明，波纹度幅值的改变对轴承的周期性振动没有改变。当波纹度幅值变大时，轴承的振动位移幅值增大。

轴承在装配过程中，都必须考虑到间隙的大小。当径向间隙数值超过出厂标准时，会造成轴承在运转过程中产生多余的晃动，使回转精度减小，还会产生振动和噪音，影响整个传动系统的运行安全可靠性；当径向间隙过小时候，轴承的会产生预紧力，此时的承载力较小，会使轴承的疲劳极限降低，轴承的使用寿命下降。因此，为了探究轴承的径向间隙对轴承的动力学的影响，取径向间隙为10 μm探究轴承的振动响应。

同样取输入转速为600 r/min，径向间隙为10 μm求解轴承的动态响应，由图3可以看出，轴承振动位移的周期没有改变，轴承的振动位移的幅值增大到3.8×10-4m；轴承的振动曲线比较稳定，没有剧烈的波动。

通过对比图2、图3和图4可以发现，滚动轴承存在波纹度和径向间隙误差时，由于滚动体等距且规则地排列在保持架上，轴承振动位移的周期是稳定的，存在波纹度误差和径向间隙时外圈在x方向上的振动位移相较于无故障时有所增大。当轴承的径向间隙和波纹度幅值增加时，输入转速一定的情况下，轴承的间隙和波纹度幅值越大，轴承的接触总变形越大，轴承的接触力增加。一定情况下，轴承的振动位移的幅值随着轴承间隙和轴承的波纹度幅值增大而增大。

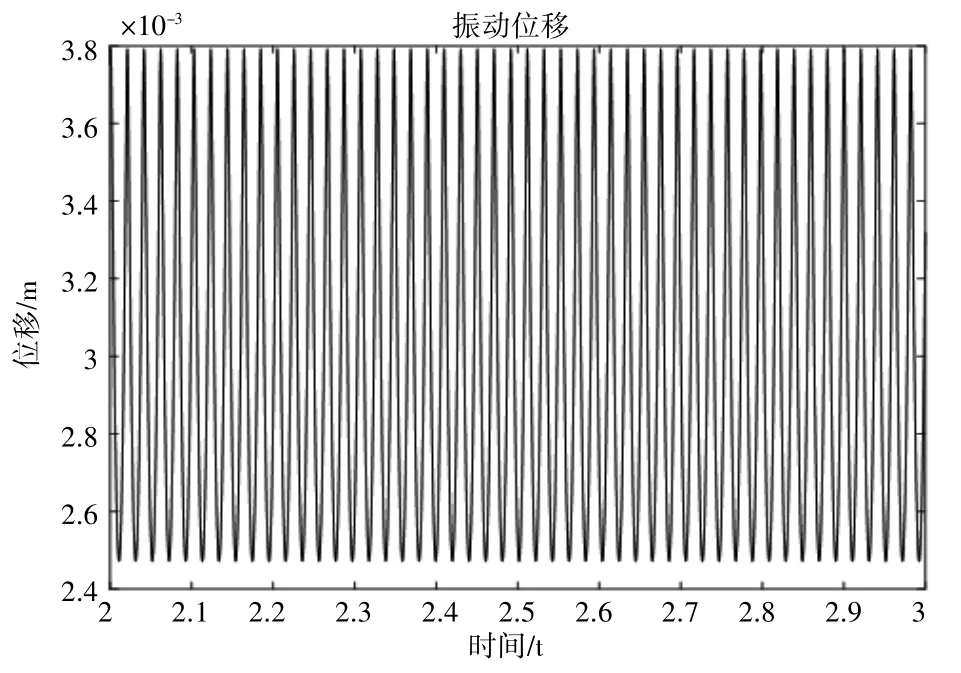
图4 径向间隙为10μm时x方向振动位移

4 结语

滚动轴承的回转精度对传动系统的运行起着至关重要的作用，但是由于制造误差和材料本身的粗糙度误差，滚动轴承的内外圈表面不可能存在绝对光滑。为了探究轴承表面波纹和圆度误差对轴承动态特性的影响，通过脉冲建立了轴承的波纹、圆度误差模型，基于牛顿第二定律建立了滚动轴承内外圈的动力学模型，通过MATLAB格库塔法求解了轴承内外圈的振动微分方程，并分析了不同工况下轴承的振动响应。

通过引入轴承表面波纹脉冲函数，在考虑径向间隙和轴承非线性接触力的影响下，建立了轴承内外圈4自由度微分方程，求解轴承的动态响应。

在轴承输入转速一定的情况下，当径向间隙和波纹度幅值增加时，内外圈的总接触变形增加，轴承接触刚度一定的情况下，轴承的振动位移增加，因此外圈在x方向上的振动位移随着径向间隙和表面波纹度幅值的增加而增大。

轴承在加工和制造过程中要控制轴承的表面加工精度，合理的分配轴承的径向间隙，以降低轴承在运行过程中的振动。