双惯量伺服系统控制参数对伺服动刚度影响

文小满，邓火生，丁可，吴锡鹏

（1.广西机电职业技术学院，广西 南宁 530007；2.广西大学，广西 南宁 530004）

0 引言

随着交流伺服系统的普及，对伺服系统的控制性能要求也随之提高。在高速高精的运动控制场合下，伺服动刚度是影响伺服系统稳定性、动态响应能力、抗干扰能力和保证加工精度的关键因素[1]。通常将阶跃负载力幅值与位置偏差的稳态值的比值定义为伺服静刚度，而负载力幅值与位置偏差的最大值的比值定义为伺服动刚度[2]。因此，研究伺服参数对伺服动刚度的影响，对提升伺服动刚度以及伺服性能具有重要意义。Alberto等通过模态试验，测量出关节模态频率和转动惯量，以此计算伺服动刚度，并提出一种基于性能指标的姿态优化方法，以提高机械加工中机器人的动刚度[3]。付睿云等人建立经编横移机构的刚度表达式，通过仿真分析位置增益、速度增益和速度环积分常数对伺服刚度和系统性能的影响，但未考虑传动机构的刚度[4]。

为了分析伺服参数对双惯量伺服系统伺服动刚度的影响，提高系统伺服动刚度，通过建立双惯量伺服系统传递函数，推导出伺服动刚度表达式，通过仿真实验分析伺服参数对伺服动刚度的影响，进而可有针对性地进行参数整定，从而提高系统的抗干扰性能。

1 双惯量伺服动刚度模型与分析

伺服动刚度是指在动态载荷下，伺服系统抵抗位置偏差的能力。因此，伺服动刚度的表达式为：

式中，ω表示动态载荷的交变频率，τ（jω）表示为动态干扰载荷，θ（jω）表示为受到动态干扰载荷伺服系统所发生的变形量。

因Ksd（jω）为复数，故用其幅值衡量伺服动刚度大小，即：

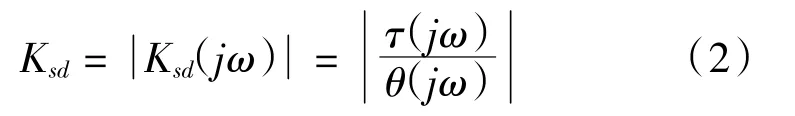
为了建立伺服动刚度模型，首先建立双惯量传动模型（图1）。其中，JM、JL分别为电机和负载的惯量；Ks为传动机构的刚度系数；N为减速器减速比；TM、TL和TW分别为电机输出转矩、负载转矩和转动轴扭转转矩；bM、bL和bs分别为电机、负载和传动机构的阻尼系数；θM、ωM、θL和ωL分别为电机和负载的角度和角速度。

图1 双惯量传动模型

由于系统中的阻尼系数很小，可将其忽略[5]。然后对系统微分方程组进行拉普拉斯变换得：

由式（4）可得双惯量系统框图（图2）。

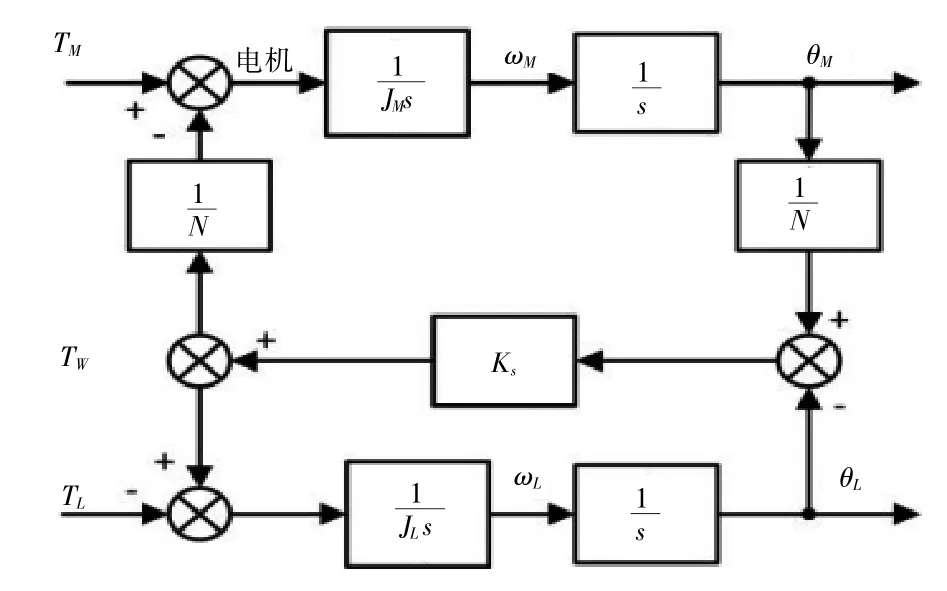
图2 双惯量系统框图

通过双惯量系统框图可以得到电磁转矩TM与电机角速度ωM之间的传递函数为：

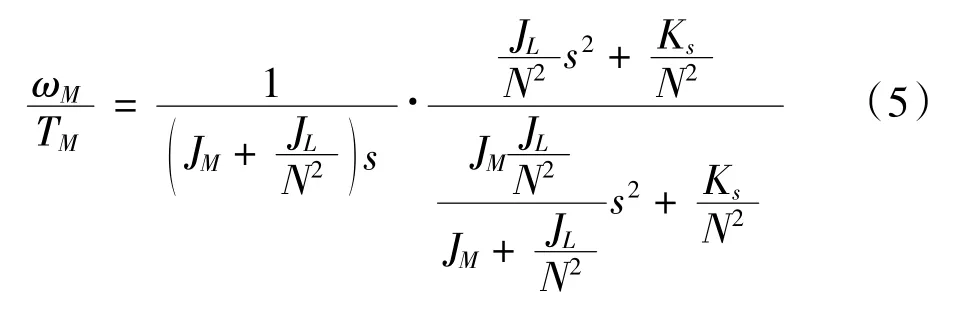
结合伺服驱动控制框图，可以建立双惯量伺服系统控制模型（图3）。其中Kpp表示为位置环比例增益，Kvp和Tvi为速度环比例增益和积分时间参数，Kip为电流环比例增益，Tii为电流环积分时间，TL为负载力和扰动力。最后可以得到单个关机伺服系统整体输出的θ（s）为：

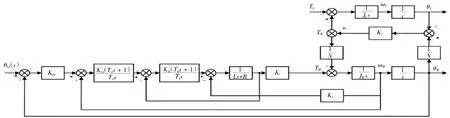
图3 双惯量伺服系统控制模型

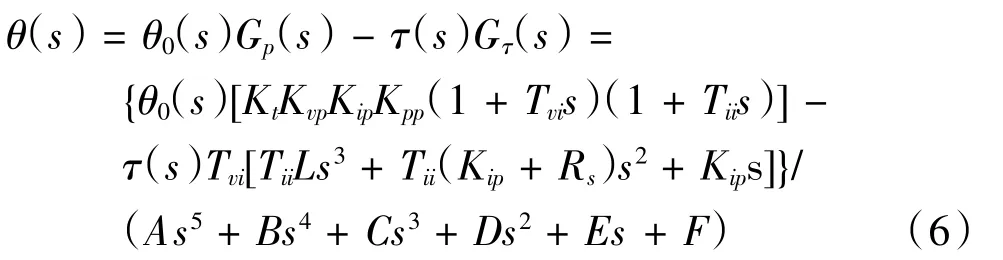
其中：

根据伺服动刚度定义可知，伺服动刚度是负载扰动TL作为系统输入，电机转子位置θM作为系统的输出，将位置输入信号当做为零处理。因此伺服动刚度的函数表达式为：

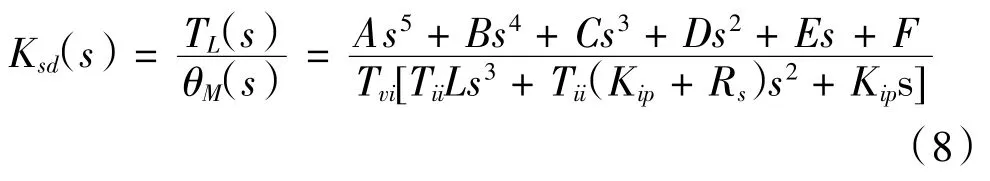
推导出的伺服动刚度表达式可看出，影响伺服动刚度的主要伺服参数有位置环比例增益Kpp，速度环比例增益Kvp，电流环比例增益Kip，速度环积分时间常数Tvi，电流环积分时间常数Tii，系统转动惯量J等。为简化分析过程只考虑位置增益Kpp，速度增益Kvp和速度环积分时间常数Tvi对伺服动刚度的影响。

2 伺服动刚度分析

2.1 伺服参数对伺服动刚度影响

为了更加直观地分析伺服参数对伺服动刚度的影响，结合上一节推导出的伺服动刚度函数表达式，改变位置增益Kpp，速度增益Kvp和速度环积分时间常数Tvi，通过Matlab仿真绘制伯德图，分析对伺服参数对伺服动刚度的影响。其中伺服系统相关参数具体数值见表1。

表1 系统参数

采用控制变量法，在保证其他的伺服参数不进行修改的前提下，依次修改位置比例增益参数Kpp、速度比例增益参数Kvp和速度积分时间常数Tvi，用伯德图分析不同伺服益参数对伺服动刚度的影响。

（1）在保证只修改位置比例增益参数，其他的伺服参数不进行修改的前提下，将位置环比例增益参数从5开始，以20为步长，一直增加至105，绘制出位置增益变化时的伺服系统伯德图（图4）。通过图4可以看出随着位置环比例增益Kpp的增大，伺服系统在2×102Hz处频段的幅值不断减小，在此之后的频率，其伺服系统的幅值不再随着位置环比例增益Kpp的变化而发生不同的变换，而是变化趋于一致。与此同时，也说明在中低频内的扰动情况下，伺服系统抵抗干扰的能力随着位置环比例增益Kpp的增大而增强，而且在干扰频率越低时，其伺服系统的抗干扰能力就越强。并且随着位置环比例增益Kpp的增大，系统的幅值下降程度也逐渐放缓。

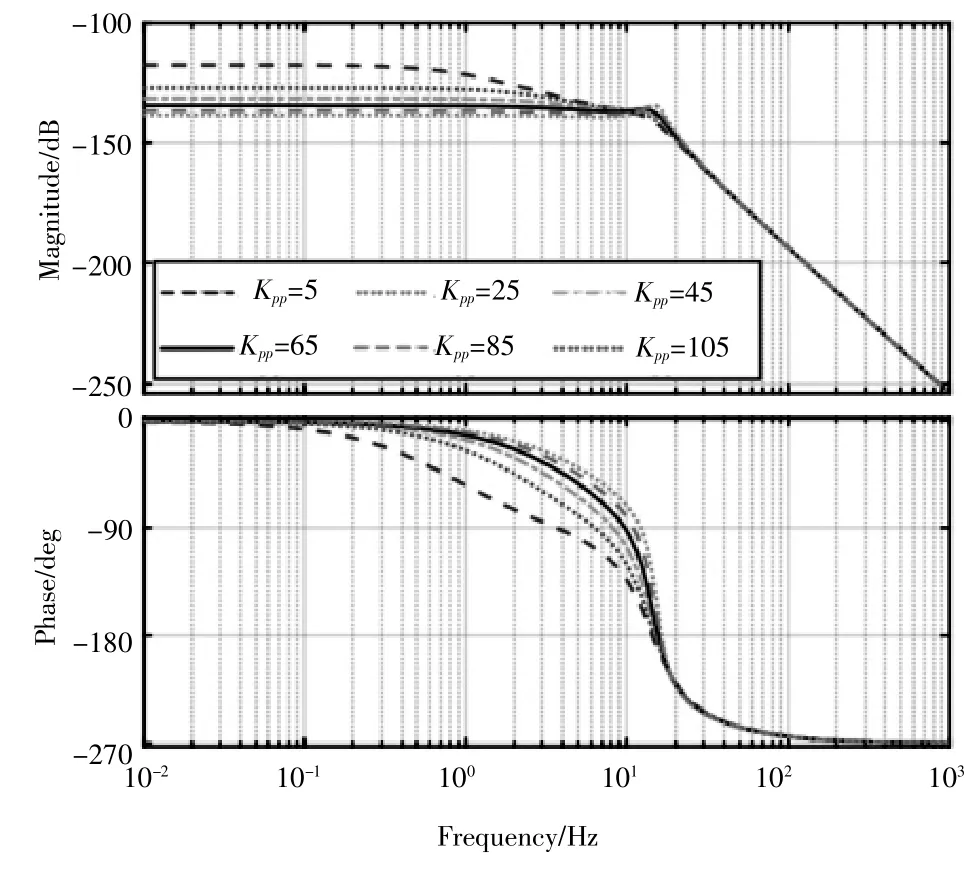
图4 位置环比例增益变化时伺服系统伯德图

（2）将速度环比例增益参数从10开始，以10为步长，一直增加至60，绘制出如图5的伺服动刚度伯德图。随着速度环比例增益Kvp的增大，伺服系统在2×102Hz处频段的幅值不断减小，在此之后的频率，其伺服系统的幅值不在随着速度环比例增益Kvp的变化而发生不同的变换，而是变化趋于一致。与此同时，也说明在中低频内的扰动情况下，伺服系统抵抗干扰的能力随着速度环比例增益Kvp的增大而增强，而且在干扰频率越低时，其伺服系统的抗干扰能力就越强。随着速度环比例增益Kvp的增大，系统的幅值下降程度也逐渐放缓。

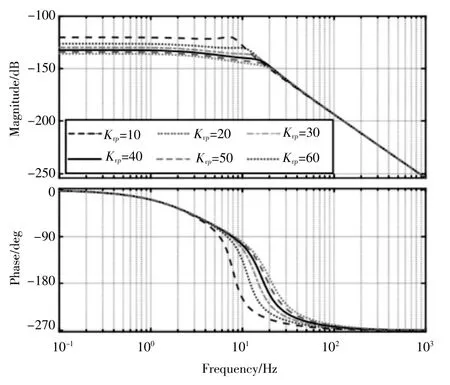
图5 速度环比例增益变化时伺服系统伯德图

（3）将速度环积分时间常数从0.1开始，以0.1为步长，一直增加至0.6，绘制出伺服动刚度伯德图，如图6所示。随着速度环积分时间常数Tvi的增大，伺服系统在低频频段的幅值不断增大，在其他段的频率，其伺服系统的幅值不在随着速度环积分时间常数Tvi的变化而发生不同的变换，而是变化趋于一致。说明在低频内的扰动情况下，伺服系统抵抗干扰的能力随着速度环积分时间常数Tvi的增大而减弱，而且在干扰频率越低时，其伺服系统的抗干扰能力就越差。并且随着速度环积分时间常数Tvi的增大，系统的幅值增大程度也逐渐放缓。

图6 速度环积分时间常数变化时伺服系统伯德图

3 结语

为了获得控制系统参数对伺服动刚度的影响，提高双惯量伺服控制系统的抗干扰能力，通过建立双惯量伺服系统控制模型，推导出伺服系统动刚度表达式。使用Matlab软件对双惯量伺服系统控制模型进行仿真，仿真结果表明对于中低频率的扰动，可以通过适当提高位置增益、速度增益和降低速度积分时间常数的方法来提高伺服动刚度，以此增强伺服系统的抗干扰能力，并为伺服动刚度的测量实验和伺服参数整定提供研究基础。