非圆曲线轮廓与规则曲面的铣削宏程序设计

黄继战，王凤清，伊登峰

（1.江苏建筑职业技术学院智能制造学院，江苏 徐州 221116；2.徐州市模具新技术工程研究中心，江苏 徐州 221116）

0 引言

一般的CNC系统只有直线和圆弧插补功能，无法直接对方程式非圆曲线进行插补加工，需要通过一定的数学处理拟合非圆曲线才能进行加工[1]。对非圆曲线与规则曲面的铣加工，数控编程方法有普通手工编程和自动编程，普通手工编程方法因节点计算工作量大致使难以编程，自动编程方法编程需要建模、图形交互设置参数等，且生成的程序非常冗长，也造成加工效率的降低[2]，同时，程序可读性和可重用性差，使用也不方便。本研究以椭圆凸台轮廓和球冠面为例，研究采用宏程序设计方程式非圆曲线与规则曲面的数控程序，只需修改曲线、曲面相关参数值，即可用于加工不同参数的曲线、曲面，具有一定的实用价值。

1 椭圆凸台轮廓铣削宏程序的设计

如图1所示的椭圆凸台零件，已知材料45#钢，粗加工和底面精加工已完成，侧面精加工余量为0.5 mm，刀具选取直径16 mm的高速钢立铣刀，要求设计该零件的椭圆凸台精铣程序。

图1 椭圆凸台零件

1.1 建立工件坐标系

建立的工件坐标系如图1所示，工件零点在工件上表面的中心。

1.2 设计走刀路线

拟合加工椭圆曲线一般采用2种方式：直线拟合非圆曲线、圆弧非圆曲线[3]。本研究采用角度变量的直线拟合加工。为了提高加工精度，选择顺铣方式，采用G41指令编程。因此，设计的椭圆凸台轮廓精加工走刀路线为P0→P1→……（椭圆的节点坐标）→P1→P0，如图2所示。

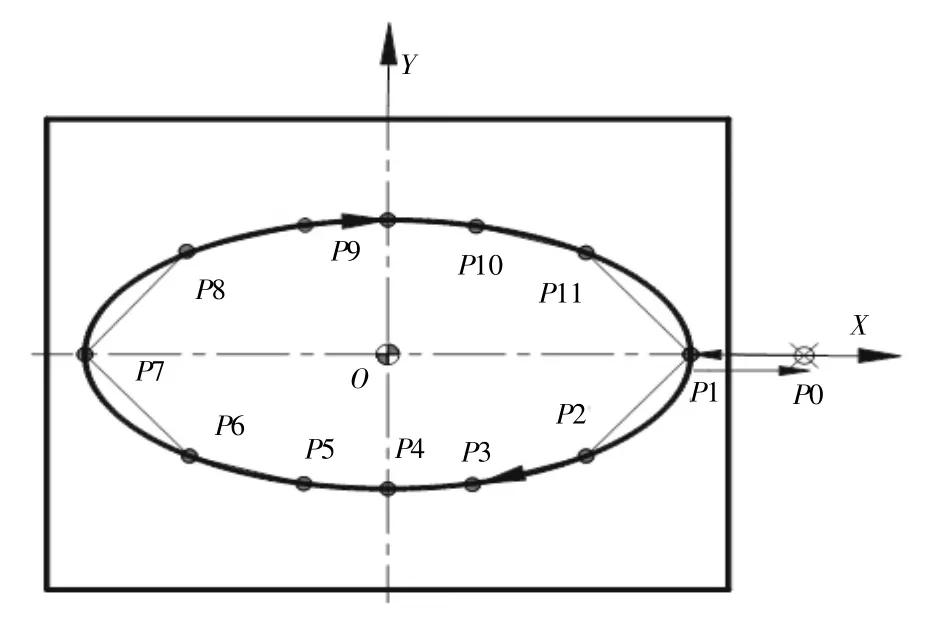
图2 椭圆凸台轮廓的走刀路线

1.3 数值计算

根据零件图和走刀路线，确定基点坐标P0（55，0）、P1（40，0）。难点在于椭圆的节点坐标如何计算，而宏程序恰好可以实现节点坐标的循环计算。

（1）建立数学模型

分析零件图形特征，确定并深刻理解非圆曲线方程含义是程序设计的关键。本例模型采用椭圆参数方程：x=a*cosθ；y=b*sinθ，其中θ为极角；a为椭圆长半轴长，为40 mm；b为椭圆短半轴长，为20 mm；（x，y）为与极角θ对应的椭圆上动点的坐标。

（2）确定自变量与因变量

根据模型，可得参数θ为椭圆方程的自变量，用变量#1表示，变量#1起始值0°，终止值-360°，自范围为0°～360°。根据允许的程编误差确定极角每次改变量，误差要求愈小，该值取值越小，误差要求越大，该值取值越大，一般取1°可满足要求，这里极角每次改变量为递减改变量，用变量#6表示，取值为-1°。

因变量为椭圆上动点的坐标（x，y），x选择变量#7表示，y选择变量#8表示，那么因变量的值用宏程序语句即可表示为：#7=40*COS[#1]，#8=#5*SIN[#1]。

（3）计算节点坐标，直线段拟合椭圆

计算节点坐标，微小直线段拟合椭圆常采用WHILE循环语句编程实现，编写步骤与内容如下：

①变量赋值

#1=0；（变量#1赋初始值0°）

#6=-1；（变量#6赋值为-1°）

②循环判断（判一判）

WHILE[#1GE-360]DO1；（判断当变量#1≥-360°时，执行循环体）

③计算节点坐标（算一算）

#7=40*COS[#1]；（计算椭圆上动点离心角为#1时的X坐标值，并赋值给变量#7）

#8=20*SIN[#1]；（计算椭圆上动点离心角为#1时的Y坐标值，并赋值给变量#8）

④走微小直线段（走一走）

G41G01X#7Y#8D01F80；（直线拟合椭圆）

⑤自变量递变（变一变）

#1=#1-1；（自变量递减1°，宏程序的引擎）

⑥循环结束符

END1；（循环结束）

1.4 程序编写与模拟

基于所述，编写的程序代码如O8451所示。该程序只需改变椭圆长、短半轴的长和极角的起始值、终止值，即可加工任意大小和任意极角范围的椭圆轮廓；而根据需要再添加局部坐标系和坐标旋转程序段，又可以实现加工任意位置和任意旋转角度的椭圆轮廓。

为便于编制此类程序代码，对拟合非圆曲线轮廓的宏程序语句，小结口诀如下：变量赋值→判一判（WHILE语句）→算一算（曲线的因变量坐标计算）→走一走（G01走直线段，拟合非圆曲线轮廓）→变一变（自变量值递增或递减）→循环结束符。

O8451；（程序名）

G17G21G40G49G80；（程序初始化）

G91G28Z0；（刀具Z轴回零）

G91G28X0Y0；（刀具XY轴回零）

G54G90G00X55Y0S600M03；（建立工件系）

G00Z50；（刀具快速至安全平面Z50）

G00Z5M08；（刀具快速至进刀平面Z5）

G01Z-5F50；（刀具切削进给至Z-5）

#1=0；（变量#1赋初始值0°）

#6=-1；（变量#6赋值为-1°）

WHILE[#1GE-360]DO1；（判断当变量#1≥-360°时，执行循环体）

#7=40*COS[#1]；（计算椭圆上动点离心角为#1时的X坐标值，并赋值给变量#7）

#8=20*SIN[#1]；（计算椭圆上动点离心角为#1时的Y坐标值，并赋值给变量#8）

G41G01X#7Y#8D01F80；（建立、执行刀具补偿，刀具走一微小直线段，拟合加工椭圆曲线轮廓）

#1=#1+#6；（自变量递减-1°）

END1；（循环结束符）

G40G01X55Y0F200；（取消刀具补偿）

G00Z50；（刀具快速至安全平面Z50）

G00Z200；（刀具快速至返回点Z200）

M30；（程序结束）

经CIMCOEdit 8软件模拟，该程序运行轨迹如图3所示。

图3 椭圆凸台轮廓程序模拟运行轨迹

2 球冠面铣削宏程序的设计

如图4所示的球冠面零件，已知材料45#钢，粗加工和顶面、底面精加工已完成，球冠面精加工余量为0.3 mm，刀具选取为直径16 mm的高速钢平底刀，要求设计该零件球冠面的精加工程序。

2.1 建立工件坐标系

建立工件系如图4所示，工件零点在工件上表面中心。

图4 球冠面零件

2.2 设计走刀路线

由于球体截断面为同心圆，加工方式采用分层切削，切削时可由上而下或由下而上进行加工[4]。此处的走刀路线采用自下而上的等高环切法（爬坡加工），这种走刀方式加工精度好，在同一高度上刀具的走刀路线为圆形，只需不断微小改变高度值即可加工出球面。球冠面走刀路线投影示意图如图5所示。

图5 球面走刀路线

2.3 数值计算

根据曲面走刀路线的设计，建立数学模型如图6所示。由零件图和模型图，可知O1C=O1B=O1F=45 mm，OB=20，OD=19.7 mm，要求出过圆弧BC上任意一点F的圆截面半径与刀位点坐标，才能编程。

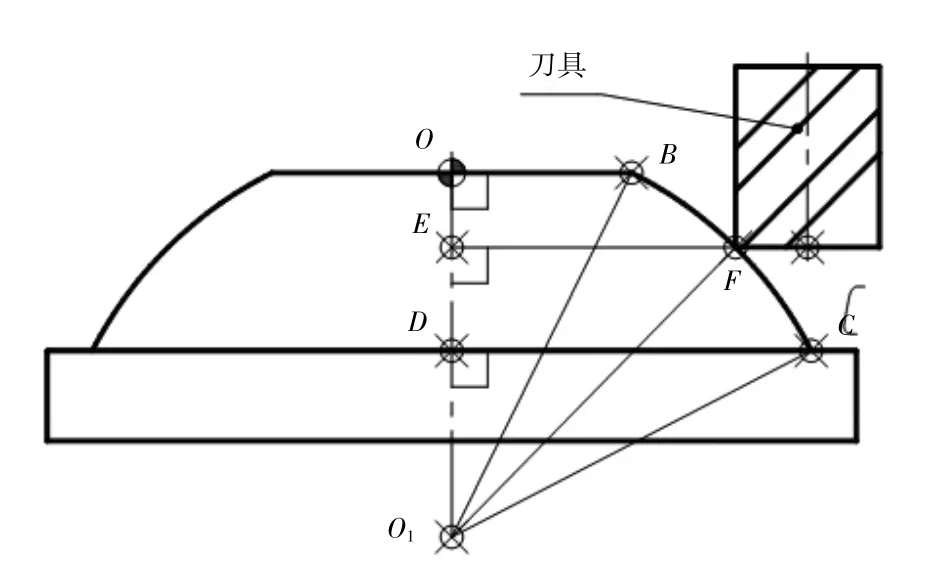
图6 数学模型

①确定模型方程。由图6几何关系可得：

在RT⊿O1EF中，由勾股定理可得：过圆弧BC上任意一点F的圆截面半径表达式为：

②确定自变量为O1E，选用变量#3表示，它的起始值为O1D，终止值为O1O需要求出。

又知，O1D=O1O-OD

已知OD=19.7mm，OB=20mm，又因在RT⊿O1OB中，由勾股定理可得：

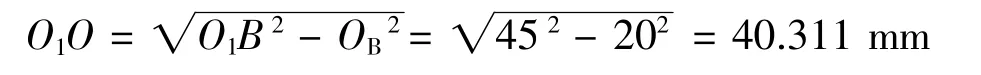
所以，

即求出变量#3的起始值为O1D=20.611 mm，终止值为O1O=40.311mm，取值范围为[20.611，40.311]。

③确定因变量为EF，选用变量#4表示，球半径选用#1表示，则EF用宏语句可表示为#4=sqrt[#1*#1-#3*#3]。

④确定刀位点坐标。结合上述和图6几何关系，即可确定刀具刀位点X轴坐标为#4+#2（其中变量#2表示刀具半径值），刀位点Z轴坐标为[-#5+#3]（其中#5表示O1O的长度）。

2.4 程序编写与模拟

基于上述，编写的程序代码如O8415所示，加工精度由O1E每次递增量的大小控制。该程序只需改变球冠面的半径、刀具半径和模型中O1E的起始值、终止值，即可加工任意大小和任意高度范围的球冠面；而根据需要再添加局部坐标系程序段，又可实现加工任意位置的球冠面。

为便于编制此类程序代码，对球冠面铣削的宏程序语句，小结口诀如下：变量赋值→判一判（WHILE语句）→算一算（计算曲面的因变量圆截面半径）→走一走（刀具先走直线段移至本层加工深度，再走圆弧铣整圆）→-变一变（自变量值递增或递减）→循环结束。

O8415；（程序号）

#1=45；（球半径）

#2=8；（立铣刀半径）

#3=20.611；（自变量#3赋初值20.611）

#5=40.311（变量#5赋值40.311）

#11=0.1；（#11表示变量#3的每次增量为0.1，其取值要与#3总增量成整数倍关系）

G17G21G40G49G80；（程序初始化）

G91G28Z0；（刀具Z轴回零）

G54G90G00X0Y0S600M03；（建立工件系G54）

Z50；（刀具快速到Z50）

X55Y0；（刀具快速到下刀点，外轮廓下刀点设置在工件外面，保证刀具凌空处下刀）

Z5；（刀具快速到R点）

WHILE[#3LE#5]DO1（当条件式成立时，循环继续）

#4=SQRT[#1*#1-#3*#3]；（计算圆截面半径）

G01X[#4+#2]Z[-#5+#3]F80；（刀具G01进给至F点）

G02I-[#4+#2]；（刀具顺铣加工整圆）

#3=#3+#11；（变量#3递增一增量#11=0.1）

END1；（循环结束）

G00Z200；（刀具抬刀至安全位置Z200）

M30；（程序结束）

经CIMCOEdit 8软件模拟，该程序运行轨迹如图7所示。

图7 球冠面程序模拟运行轨迹

3 程序分析

宏程序设计采用刀具半径补偿编程，控制零件尺寸精度仅需通过改变刀具补偿值D即可，程序本身不变。D=R刀+修正量，修正量=±（实际尺寸-理论尺寸）/2，外轮廓取-，内轮廓取+。以椭圆为例，精加工时实测椭圆长半轴尺寸为80.1 mm，长半轴尺寸理论值为80 mm，出现超差，修改刀具半径补偿值D为7.95 mm即可（D=8+[-（80.1-80）/2]=7.95）。

宏程序控制零件加工的形状精度仅需在程序中通过设置合适的自变量的增量值即可，该值愈小精度越高，程序本身不变。而自动编程时该增量值越小，程序越长。以椭圆为例，控制椭圆形状精度的是离心角的每次增量值，取值为-1°时，宏程序共用8个程序段，而同样的条件，自动编程时则生成的程序段多达360条，非常冗长，可读性差。

对同一个方程曲线或曲面，首次设计宏程序需要花费一定的时间，但后续在控制零件曲线或曲面的加工精度、大小等方面，宏程序仅需修改参数值即可，编程时间可忽略不计。而自动编程在上述情况下均需要重新编程，后续自动编程与首次自动编程所花费的时间基本一样，重复劳动，致使效率低下。

4 结语

非圆曲线轮廓与规则曲面铣削宏程序的设计仿真与实践表明，非圆曲线轮廓与规则曲面的铣削宏程序，短小精悍有较好的通用性和柔性，使用方便，易于控制零件加工精度，避免重复编程，提高了编程效率；介绍的程序设计方法，行之有效，降低了宏程序编程的难度，对同类宏程序的设计具有一定的指导意义。