气井零液流量流动模拟实验及模型应用研究

罗程程， 靳 悦， 刘永辉， 杨杰友, 杨建英， 王 强， 叶长青

1西南石油大学 2油气藏地质及开发工程国家重点实验室 3中国石油长庆油田采油五厂 4四川长宁天然气开发有限责任公司 5中国石油西南油气田分公司气田开发管理部 6中国石油西南油气田分公司工程技术研究院

0 引言

天然气的开发总是伴随着水和凝析油的产出。而随着气藏的开发，地层压力会不断降低，产气量也会随之降低[1]。当气量降低到某一界限时会使得气流速无法连续携液，从而导致液体在井筒中聚集形成积液，使得井筒压力梯度大幅增加，甚至造成气井“水淹”，进而严重影响气井最终采收率[2- 4]。当井筒积液后，井筒出现明显的压力梯度拐点，井口也不会产液或者少量产液，这种现象称之为零液流量流动。井筒零液流量流动是气井积液后井筒中一个特殊的气液两相流动现象，准确掌握零液流量流动规律对于认识气井井筒积液规律，揭示气井积液机理及实施排水采气措施有着重要意义[5- 7]。

目前，关于零液流量流动规律的研究较少。Kokal和Stanislav[8]在近水平管道中开展了“零液流量”实验，实验中观察到间歇流和分层流，而Amaravadi等[9]建立了零液流量压降机理模型，只是针对基于近水平管的流动所建立。刘磊等[10]开展了零液流量气提实验，建立了两相流水动力学模型，将流动简化为段塞流形式，模型计算方法复杂且未对所涉及的闭合方程进行校对。魏纳等[11]开展了气井零液流量的气提实验并拟合了持液率预测公式，但模型采用气液表观流速建立且未与实验数据进行对比，无法验证模型的可靠性。刘永辉等[12]建立了基于零液流量流动条件下的气井积液诊断方法，其本质仍为稳定气液流速的两相流动计算。王武杰等[13]基于微倾斜管中的零液流量实验，建立了考虑倾斜角的界面摩擦因子模型，进而建立了携液临界气流速新模型，认为临界气流速与滞留液量的多少无关。

综上所述，目前关于“零液流量”流动的研究还不够完善和系统。在实验方面，不同参数对“零液流量”流动的影响规律尚未摸清，“零液流量”流动与稳定气液流速流动之间的关系也有待进一步研究。在模型方法，仍缺乏准确全面地预测气井中零液流量流动压降的模型。为此，本文开展了零液流量流动实验，研究了液面高度、气流速和管径对井筒持液率的影响，提出了零液流量持液率预测模型；基于此模型，建立了井筒积液高度预测方法，为揭示气井连续携液机理提供基础。

1 零液流量模拟实验

1.1 实验装置及实验方法

为了深入研究零液流量流动规律，研制了一套可视化的两相流动模拟实验装置。实验管柱主体长5 m，采用透明有机玻璃管组成，管段主体可拆卸或组装不同管径的玻璃管。实验介质为空气和水，在环境温度为20 ℃、标准大气压条件下开展。实验系统由进气系统、进水系统、管路系统和测控系统四部分组成，见图1。

图1 零液流量流动实验装置图

进气系统由空气压缩机和储气罐组成。储气罐体积达2 m3，空气压缩机将气体压缩并存储至储气罐中，最高储气压力可达4 MPa，以保证供气稳定。进水系统由水箱和液相泵组成，水箱内的液体通过液相泵泵入实验回路。在测控系统中，气流量由气体流量计测量，管道压降则由安装在管道顶部和底部的压力传感器记录。

实验过程中，所有流动现象均采用高速摄像机实时记录，以分析不同流动状态下参数对流动规律的影响。“零液流量”流动时，井筒液量未被带出管柱，实验过程中总液量保持一致，因此实验持液率可根据预设静液柱高度与流动时实测“动液面”高度比值计算得到。

实验中预设两组静液柱高度(50 cm、100 cm)来模拟不同积液高度对流动的影响。考虑气流速过高时，管柱中会存在液滴夹带，以及本实验装置高度较低，会导致部分液体随着气体流出管道，因此本文将气流速范围设定为0.05～4 m/s，可保证气液流动过程中覆盖到泡状流、段塞流和搅动流等不同流型。为了研究管径对流动的影响，选择内径为40 mm、50 mm、61 mm油管开展管径敏感实验分析。

实验流程如下：①定实验管柱尺寸并在管柱中预存一定高度的液体，调节气量至目标值，待流动稳定后记录动液面高度和流动型态，测量井筒压力，完成该组实验；②改变气量开展下一组实验，直至完成该尺寸管道和液柱高度下的实验；③随后依次更改管柱尺寸和液柱高度，直至完成实验测试。

1.2 实验结果及分析

在零液流量模拟实验中，可观察到泡状流、段塞流、搅动流三种流型，见图2。随着气流速增大，动液面高度越高，与之对应的流型也逐渐发生变化。可以看出，零液流量流型变化规律与稳定两相流动变化规律一致，不同流型所呈现出的流型特征与稳定液流速的两相流条件下是相同的，其变化规律与稳定两相流动变化规律也一致，表明零液流量流动与稳定两相流动的一致性。

图2 零液流量流型快照(管径61 mm)

静液柱高度分别为50 cm和100 cm时，流动测量的持液率对比情况见图3。在相同气流速下，不同静液柱高度持液率是几乎相同的。结果表明零液流量持液率大小仅与气流速相关，与液柱高度无关。两组静液柱高度测量的对应动液面高度均呈2倍的比例关系，这是因为相同气流速下，向上流动时的带液(穿过液相)能力是一定的，那么持液率就会保持一定，井筒液体越多，动液面则越高。

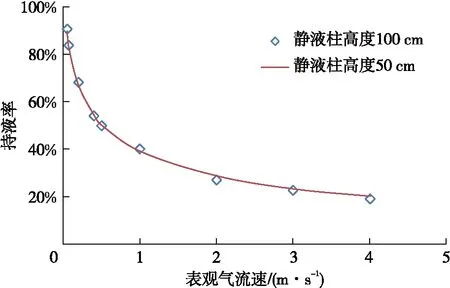
图3 静液柱高度对零液流量持液率的影响(管径61 mm)

不同管径条件下持液率随着表观气流速的变化曲线见图4。整体上来看，当气流速较高时，管径对持液率的影响相对较小。随着表观气流速的增加，井筒持液率逐渐降低，在气流速低于2 m/s时降低幅度更大，这是气相由连续相向非连续相转化的结果。当液相为连续相时，液体更易在井筒聚集，气量的略微增大就会造成气体占比的迅速增加；而当气相逐渐成为连续相后，液体更多地分布在管壁周围，被携带出井筒则需要更大的拖曳力。从图4中还可以看出，管径越大，相同气流速条件下持液率越大，尤其是在低气流速时(vSG<1 m/s)管径对持液率影响相对更大，其原因是管径越大，气液两相之间滑脱也越大，液相为连续相时气相更易向上流动，持液率更高。

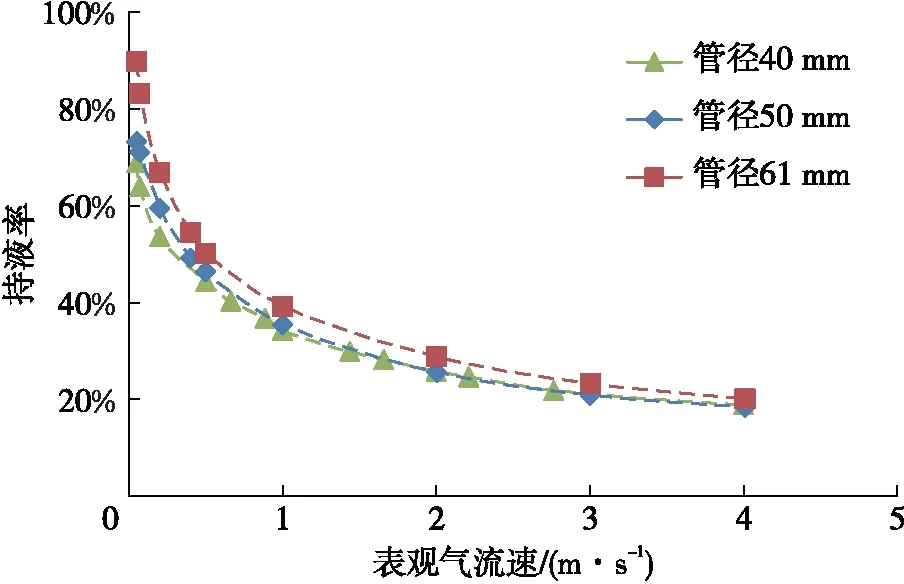
图4 零液流量持液率随表观气流速关系曲线

相同气流速下持液率随管径变化曲线见图5，可以看出，持液率与管径几乎呈现线性变化关系。

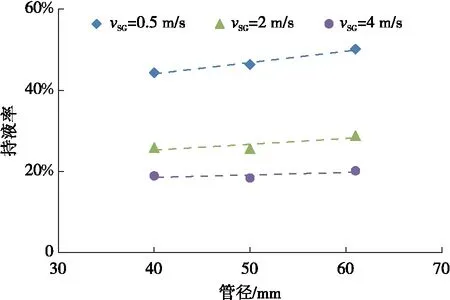
图5 持液率随油管尺寸关系曲线

零液流量流动时总压降、重力降和摩擦阻力降随气流速的变化曲线见图6。总压降由压力传感器测量，重力降则根据测量的持液率计算，摩阻降采用间接方式求得，忽略动能项，摩阻降可根据总压降与重力降求得。从图6中可以看出，随着气流速增加，总压降和重力降均有所增加，这是因为底部压力传感器以下的液体被带到测压段所造成。在测量过程中，摩阻降还包括了动液面以上气柱摩阻降，因此，气液两相流动段的流动摩阻降会更小。因此，零液流量流动压降计算的关键核心为准确预测持液率。

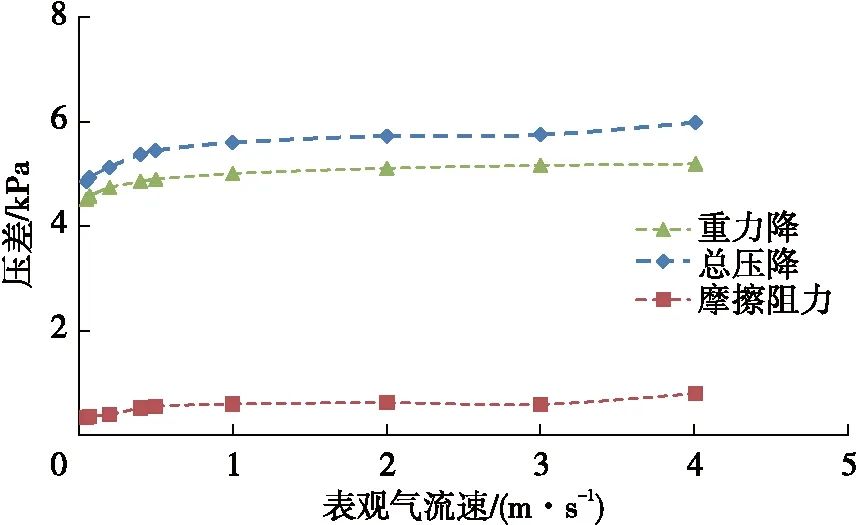
图6 零液流量流动压降变化曲线(管径61 mm)

2 气井零液流量持液率模型

对于气井而言，流体性质相对单一，因此本文忽略其对持液率的影响。由上述实验分析可知，低气流速时井筒中压力降由液柱重力降主导，可忽略摩阻降。“零液流量”条件下井筒的压力降可以由持液率近似求得，而持液率是与气流速和油管尺寸相关的函数。因此，基于持液率与气流速与油管尺寸的关系曲线，构建持液率模型经验表达式[13]：

HL=a(bD+c)(dlnvSG+e)

(1)

式中：HL—持液率，%；a，b，c，d，e—拟合系数；D—油管尺寸，m；vSG—气流速，m/s。

低压实验和高压井筒中气相密度存在巨大差异，导致相同气液流量下气液两相之间界面特征不同，与之对应的流型与压降也不尽相同，因此有必要采用合理的准数表征不同压力下两相流动规律的相似性，实现不同压力下流动的归一化处理。王琦[15]指出采用Hewitt 和 Roberts[16]提出的准数能够较好处理压力对流动影响，因此本文采用该准数来表征高低压流动的相似性：

(2)

式中：NvSG—气相准数，%；ρg—气相密度，kg/m3。

式(1)可变为：

HL=a(bD+c)(dlnNvSG+e)

(3)

采用实验数据对式(3)进行参数拟合，得到拟合模型：

HL=1.22(5.4D+0.27)(-0.1lnNvSG+0.6)

(4)

模型对比结果如图7所示，从不同油管尺寸中随着气流速的变化趋势来看，模型能够随着参数变化而准确地变化，模型预测绝对误差也仅为3.5%，验证了模型的精度和可靠性。

图7 模型评价

3 井筒积液高度预测方法

判断气井是否积液并进一步预测气井积液程度是指导排采措施合理实施的关键。零液流量持液率模型能够为常规两相流动模型提供补充，为气井稳定生产提供理论支撑。根据Lea等人[17]的研究，对于未下封隔器的积液气井而言，除了部分气井会产生低频的压力波动，造成环空中出现高度动态变化的液柱外，其余油套压相对稳定的气井中油套环空中为纯气柱。因此，可利用环空气柱压力和套压值计算井底流压，再利用本文所建零液流量持液率模型和生产参数即可判断积液程度。具体方法如图8展示的动液面高度预测示意图：首先利用套压值计算环空静气柱压力曲线pc-pwf，再利用计算井底流压值pwf和零液流量模型分段迭代计算可得井筒压力曲线pwf-pt′，如果计算油压pt′等于实际油压pt则表明气井不积液，反之则积液。而对于积液的气井，基于井口油压可计算动气柱曲线pt-O，与pwf-pt′曲线的交点位置则为动液面高度。

图8 动液面高度预测示意图

对于环空而言，环空静气柱压力梯度曲线pc-pwf可利用式(5)计算：

pwf=pc+10-6ρggH

(5)

式中：pwf—井底流压，MPa；pc—套压，MPa；g—重力加速度，9.81 m/s2；H—静气柱高度，m。

对于存在“零液流量”流动的气井而言，仍会有少量液体以液滴形式夹带于气体中夹带的形式携带出井筒，因此动气柱压力曲线计算时需采用夹带液滴的气液混合密度计算重力降。动气柱压力梯度可表示为：

(6)

式中：Δp1—动气柱压力梯度，Pa/m；ρC—夹带液滴的气液混合密度，kg/m3；f—摩擦阻力系数；v—夹带液滴的气体流速，m/s；D—油管管径，m。

忽略零液流量流动的摩擦阻力，其压力梯度可表示为：

Δp2=HLρLg+(1-HL)ρGg

(7)

式中：Δp2—动液面以下两相压力梯度，Pa/m。

4 现场验证及运用

选取四川气田X井进行验证分析。X井的井深1 710 m，采用62 mm油管生产。由生产测压可知，如图9所示，井底流压为2.24 MPa，地层温度为52 ℃，井筒积液的液面位置在1 500 m左右，对应测压为1.79 MPa，液面以上为气柱。测压时，生产油压为1.56 MPa，油温为21 ℃，套压为2.07 MPa，产气量为0.96×104m3/d，产液为0.2 m3/d。

采用本文提出方法对积液高度进行预测。首先计算套管气柱曲线，然后利用计算井底流压计算油管流压曲线，同时根据井口油压计算油管气柱曲线，两者交点处油压为1.78 MPa，深度为1 370 m左右，与实际测量液面深度1 500 m相差仅130 m，计算绝对误差为8.7%。从流压曲线和实际测压来看，两者拟合度较高，验证了所建模型的准确性。同样地，基于目前生产现状对不同生产情况进行了分析，如图9所示，产量越高，相同井底流压条件下对应的动液面位置越高，与之对应的持液率也会越低，表明积液程度减弱；产气量为2.2×104m3/d时计算油压略大于实际油压，表明该油压条件下气井不积液的气量界限在2.0×104～2.2×104m3/d之间。从动液面高度随着产气量的变化来看，井筒积液初期动液面高度对产气量更加敏感，液面位置随产量变化而变化更快，分析可为气举和泡排等排水工艺提供重要指导作用。

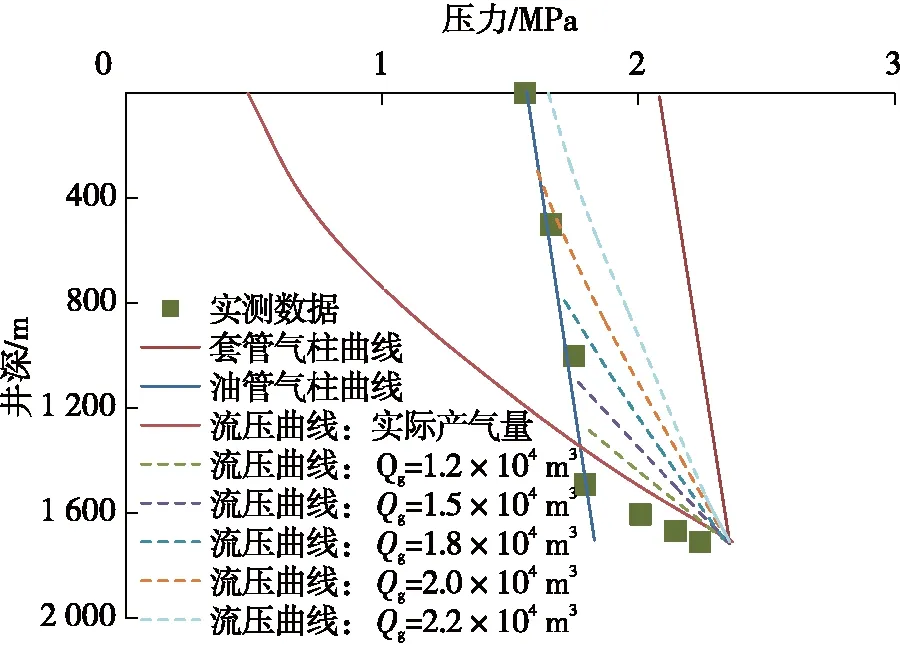
图9 X井积液高度预测与分析

5 结论

(1)实验结果表明，零液流量流动存在泡状流、段塞流和搅动流，流型变化与稳定两相流具有连续性；而静液柱高度对零液流量持液率无影响，只影响动液面的高度。

(2)建立了采用Hewitt & Roberts准数的零液流量持液率模型，模型与实验误差为仅为3.5%，与实际气井误差为8.7%，为现场积液高度的预测提供了理论依据。

(3)建立的井筒积液高度预测方法采用四川气田某气井进行验证和分析,结果表明该方法能较为准确地预测积液高度和判断气井积液与否。