基于Douglas-Peucker融合闵式距离的锂电池健康因子提取及SOH预测

陈万利，张 梅，冯 涛

（安徽理工大学，安徽 淮南 232001）

锂离子电池作为最常用的储能器件之一，被广泛应用于航天、新能源汽车、移动电话以及便携式电子设备等领域[1-3]。由于电池内部的化学反应以及外部环境的影响，电池的使用寿命随着时间的推移逐渐衰退老化甚至失效。锂离子电池的衰弱退化无疑增加许多电子设备的维修成本，而且电池的突然失效易导致新能源汽车等大型设备停止工作，甚至导致重大事故的发生[4-5]。因此及时预测电池的健康状况及失效时间有利于及时规划和管理电池，并及时更换失效电池进而降低事故发生概率，保证设备运行的安全性及可靠性。因此精确预测锂离子的SOH(state of health)及电池的剩余使用寿命(remaining useful life，RUL)对电池的维护及更换起着主要作用，锂离子电池的SOH 及RUL 预测已然得到广泛关注[6]。

然而锂离子电池运行过程中的健康因子提取困难，这无疑导致电池的SOH 及RUL 预测不精确。如何建立有效的特征工程从而实现对电池的健康因子的提取及筛选成为锂离子电池研究中的重点和难点。

锂离子电池的SOH 及RUL 预测大致可分为统计分布、基于数据驱动、基于模型驱动3种方法[7]。基于数据驱动的方法通过建立特征工程，利用热门的机器学习神经网络等方法建立电池SOH 及RUL与健康因子之间的映射关系，从而实现电池SOH及RUL 预测任务。由于近年来人工智能的大力发展，基于数据驱动法的电池SOH 预测得到越来越多的关注和应用[8]。

数据驱动法预测电池SOH 及RUL 的人工智能算法主要包括极限学习机(ELM)、支持向量机(SVM)、BP神经网络和集成算法(如XGboost)[1,9-10]。李洁等[11]将差分电压曲线和充放电曲线作为电池容量退化特性，并利用Elman 神经网络对电池RUL实现预测。黄鹏等[12]利用GA-Elman 神经网络对电池容量进行预测，所得结果对不同电池有较强的适应性。杨彦茹等[13]利用Pearson和Spearman法分析健康因子与容量之间的相关性，然后利用CEEMDAN算法将健康因子进行分解所建立的特征工程。王英楷等[14]利用一维卷积(1DCNN)联合LSTM算法对电池SOH 预测，该方法可有效提高单一LSTM 算法的性能。于明等[15]利用Wavelet 降噪和支持向量机实现对电池RUL 预测，且利用改进鸡群算法(ICSO)改进SVM 模型，提升了SVM 模型的性能。以上文献结果表明，上述方法对锂离子电池领域的贡献突出，为电池SOH 和RUL 预测提供了多种思路和方法，但是这些方法在特征工程中建立电池SOH预测的精度上仍有改进余地。本文通过研究电池各循环属性的曲线，对电池的循环属性建立了特征工程，提出新型的锂离子电池特征提取算法，在SVM模型上实现对电池SOH及RUL的预测。

为解决电池的健康因子提取困难，无法全面地提取电池中有效的健康因子的问题，本文利用改进的Douglas-Peucker算法融合闵式距离对电池建立特征工程，并级联DBSO 算法进一步提取健康因子，剔除冗余特征，提高模型性能，防止模型陷入过拟合。进一步地，本文提出DSBO-SVM 模型，利用提取的健康因子对电池SOH及RUL进行预测。针对不同充放电策略，本文采用多个数据集进行验证，所得结果表明本文所建立的特征工程在不同充放电策略均可适用。

1 算法描述

1.1 改进的Douglas-Peucker算法

Douglas-Peucker 算法通过提前设定阈值将曲线分段，最终得到曲线的近似线段[16]。

由于充电循环过程中锂电池的老化，造成每次循环所测得属性的时间步不对齐，序列长短不一致。传统Douglas-Peucker算法在属性的时间步不对齐，序列长短不一致情况下，无法对每个属性提取相同维度的特征。

传统的Douglas-Peucker算法无法定维度提取曲线特征，在确定阈值threshold 的大小时，不同充电循环的属性曲线时间步不对齐，序列长短不一致，可能造成不同充电循环利用Douglas-Peucker算法所提取的特征长度、位置不一致。所提取的特征长度、位置不一致会导致神经网络无法利用所提取的特征训练，所提取的特征作用不大。因此需对Douglas-Peucker算法进行改进。

由于传统Douglas-Peucker 算法根据阈值threshold 的大小来确定曲线最终所保留的特征维度。因此无法做到在不同曲线提取指定维度的特征。

为解决传统的Douglas-Peucker算法对锂电池不同充电循环的属性所提取的特征长度、位置不一致问题，本文提出一种能在不同曲线中提取相同维度的Douglas-Peucker 算法。具体流程如图1所示。

图1 改进的Douglas Peucker算法流程图Fig.1 lmproved Douglas Peucker algorithm flow chart

1.2 DBSO算法

1.2.1 BSO算法

头脑风暴优化算法(brain storm optimization algorithm，BSO)是最早由史玉回教授[17]2011 年提出的一种智能算法，它主要模拟人类创造性解决问题过程中的群体行为。其采用聚类思想搜索局部最优，通过局部最优的比较得到全局最优。采用变异思想增加了算法的多样性，避免算法陷入局部最优，适合于解决多峰高维函数问题。

BSO变异主要有4种方式，分别是：①在随机一个类中心，即该类最优个体上添加随机扰动产生新的个体；②在随机一个类中随机选择一个个体添加随机扰动产生新的个体；③随机融合两个类中心，并添加随机扰动产生新的个体；④随机融合两个类中随机的两个个体，并添加随机扰动产生新的个体。

1.2.2 DBSO 算法(difference-mutation brain storm optimization)

DBSO算法与经典的BSO算法整体结构相同，只是在第4步中采用差分变异代替高斯变异。经典的BSO算法中，采用高斯变异，新个体产生公式(1)为

式中，xnd为新的d维个体，xsd为选中的个体；N(0,1)d为d维标准正态分布；ξ为高斯函数的系数

式中，T和t分别表示设置的最大迭代次数和当前迭代次数；k可以调节lg sig()函数的坡度；R(0,1)是0～1的随机值。

在该变异中，初期能符合要求，但到了后期高斯变异的变异系数趋于固定，就不能很好地捕捉搜索特征了[18]。为此，DBSO算法采用差分变异。

在人类头脑风暴过程中，前期每个人的想法都会有很大差异。在创造新观念时，要考虑到现有观念的差异。因此，DBSO算法通过差分变异来确定变异步长，具体操作如式(3)所示

式中，y为产生的新个体；R为0～1之间的随机数；Ld与Hd为搜索空间的上下界；pr为设置的开放性概率；rand()为产生随机数的函数；x为选择的个体；xa与xb为局中选择的两个不同个体。

1.3 SVM原理

SVM 模型通过构建超平面，将数据映射至高维空间，使数据在超平面下不同类别数据距离最大化。SVM 模型广泛用于模式识别、故障诊断、数据回归[19]。由于SVM 模型在中小量样本的时候容易得到数据和特征之间的非线性关系，可以避免使用神经网络结构选择和局部极小值问题，因此SVM模型常用于小样本数据的分类与回归。

SVM模型的核心思想是最大化超平面的间隔，因此要建立相应的目标函数与约束条件。

假设有N个训练样本{(xim,yi)}(i=1,2,…,N)，yi为第i个样本的标签，xim为第i个样本的m维特征空间。点xim到超平面(w，b)的几何间隔为

式中，yi为第i个样本的标签，取值只有1和-1。当第i条数据被正确分类时，yi取值和wxim+b取值的正负一致，几何间隔为正；当被错误分类时，yi取值和wxim+b取值的正负相反，几何间隔为负。

定义几何间隔中最小的为

因此可以得到间隔最大化问题的目标函数

并遵循如下约束条件

SVM 模型的核函数采用径向基(radial basis function kernel，RBF)核函数。

1.4 基于Douglas-Peucker 的健康因子提取及DBSO-SVM预测模型

SVM模型受参数影响较大，惩罚因子c和核函数参数g的选择直接影响了SVM 的分类精度和泛化能力[20]。本文利用SVM 模型对电池寿命进行预测，利用DBSO 算法优化SVM 模型的惩罚因子c和核函数参数g，以使诊断模型性能提高。针对电池寿命预测，本文构建了DBSO-SVM 模型，如图2所示。

图2 基于Douglas-Peucker的健康因子提取及DBSO-SVM预测模型Fig.2 Douglas-Peucker based health factor extraction and DBSO-SVM prediction model

基于Douglas-Peucker 的健康因子提取及DBSO-SVM 预测模型主要由特征处理、DBSO 优化和SOH 预测3 个部分组成。数据特征工程的建立主要利用Douglas-Peucker算法融合闵式距离并级联DBSO 编码器对电池每个循环的健康因子提取；DBSO 优化部分是利用DBSO 模型对SVM 模型的几个超参数进行寻优，得到最优参数；SOH预测部分是训练、测试SVM模型，对电池SOH进行预测并进行模型评价。

2 实验方案及数据获取

2.1 仪器设备

利用新威电池测试仪对电池充放电过程中的参数进行检测。检测参数包括：充电、静置、放电过程中的相对时间、电压、电流、容量和功率。利用恒温箱将电池周围环境恒定至15 ℃。

电池采用18650电池作为待检测设备。具体参数见表1。

表1 电池详细参数Table 1 Battery detailed parameters

2.2 实验步骤

①恒流充电至4.2 V，恒压充电至充电电流小于0.2 A。

②静置10 min。

③恒功率6 W放电，截止电压设置为2.7 V。

④静置10 min。

⑤跳转步骤①循环197次。

实验装置如图3所示。

图3 实验设备Fig.3 The laboratory equipment

2.3 实验数据

本文建立数据A和数据B，以数据集A作为研究对象，建模预测模型。为验证本文所建立的模型具有通用性，利用数据集B再次建立相同的特征工程，观察数据B的预测效果。

数据集A：取本次实验的检测参数，包括充电、静置、放电过程中的电压、电流和功率指标作为预测模型中的自变量。取每次循环的放电总容量(mAh)作为预测模型的预测对象。

数据集B：来自NASA 预测中心(prognostics center of excellence，PCoE)的第1 批数据集，B0005、B0006、B0007、B0018。该实验记录了锂电池充放电时的电压、电流、阻抗值和温度。充电过程：以1.5 A 恒流充电，当电压达到4.2 V 时，改为恒压充电，直至充电电流下降到20 mA结束充电。放电过程：以2.0 A 恒流放电，当电池电压值下降到2.5 V时停止放电[21]。

3 特征工程建立及全信息健康因子提取

以数据A为研究对象，由于充电循环过程中锂电池的老化，造成每次循环所测得属性的时间步不对齐，序列长短不一致，以充电的功率属性为例，如图4所示。

图4 充电的功率属性不同循环曲线Fig.4 Different cycle curves of charging power attribute

由于每次循环同一时间步下所测的属性位置不一致，无法利用智能算法和机器学习方法提取特征，因此直接利用电池所测属性，无法建立相应的预测曲线。

本文首先利用所测电池数据建立特征工程模型，其次利用所建立的特征工程模型提取数据特征，最后建立预测模型。

本文采用改进的Douglas-Peucker算法提取电池各属性特征，以闵式距离和特征维度大小作为提取的特征维度指标，建立决策函数，通过决策函数值确定最终提取的属性维度。

数据集A每次充放电循环包括充电实验的电压、电流和功率，包括放电实验的电压、电流和功率共6个属性。

数据集B每次充放电循环包括充电实验的Voltage measured、Current measured、Temperature measured、Current charge 和Voltage charge，包括放电实验的Voltage measured、 Current measured、 Temperature measured、 Current load和Voltage load共10个属性。

两个数据集每个属性的每次循环均为包含时间序列的曲线，每次循环的时间序列长短不同。由于阻抗属性在实际使用中测量较为困难，预测不包含阻抗属性。

由于相邻循环下的各属性曲线相似，因此相邻曲线上的明显特征变化不大，整体呈连续形状，如充电电压属性的初始电压，其曲线如图5(a)所示。

利用改进的Douglas-Peucker算法，将每次循环所得的属性曲线提取指定维度时，若将曲线压缩的维度过大，会产生所提取特征位置不一致，如将充电电压属性压缩成8 维，其第4 维属性如图5(b)所示。

图5 充电电压属性不同位置的循环曲线Fig.5 Cycle curves of charging voltage attributes at different positions

据图5(b)所示，相邻充电次数的第4 维属性多处不连续发生突变，显然由于提取特征位置不一致所造成。特征提取位置不一致会导致不同充电循环所提取的属性位置不同，从而导致所提取的电池健康因子并无实际意义，因此尽量避免此类问题出现。

由图5(b)可知，当出现特征提取位置不一致时，曲线易出现不连续现象。不连续现象会导致相邻曲线之间的闵式距离值增大，因此以闵式距离作为决策值，利用闵式距离判断不同循环所提取的特征是否位置相同。

以数据集A的充电电压属性为例。

首先利用改进的Douglas-Peucker算法将电池各循环的充电电压属性压缩成n维，得到197 条n维的曲线。

其次将n维曲线映射到n维空间中，利用闵式距离公式计算第i+1次循环的曲线和第i次循环的曲线之间的距离值。

加绝对值的闵式距离公式(8)如下：

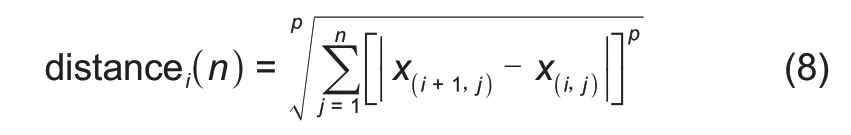
式中，n代表将曲线压缩成n维。x(i,j)为第i次循环经改进的Douglas Peucker 压缩后的n维曲线的第j维值。x(i+1,j)为第i+1次循环经改进的Douglas-Peucker压缩后的n维曲线的第j维值。distancei(n)为第i次循环经改进的Douglas-Peucker压缩后的n维曲线与第i+1 次循环经改进的Douglas-Peucker压缩后的n维曲线的闵式距离值。p为实数中任意数，本文p=3。

最后累加所有的距离值，得到最终的总距离值D(n)。

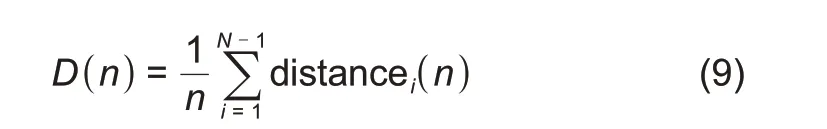
式中，N代表电池循环次数，本实验N=197。D(n)为经改进的Douglas-Peucker 压缩后的n维曲线闵式距离值的总距离值。

充电电压属性提取不同特征维度时的闵式距离的总距离值如图5所示(起始维度为2)。

由图6 可知，在利用改进的Douglas-Peucker算法提取3 维及以下的特征时，闵式距离值最小，说明所提取的特征曲线更为光滑连续，但所提取的维度低，所包含的特征信息也较少。

图6 充电电压属性不同维度的闵式距离值Fig.6 Minkowski distance values of different dimensions of charging voltage attribute

特征信息与维度大小正相关，维度越大，特征信息越多，维度越小，特征信息越少。因此根据闵式距离值和当前维度值建立决策函数。根据函数值决定最终维度，由于维度越高，特征信息越多，因此当前维度与最终维度成正向相关。由于最终维度的闵式距离值越小越好，因此最终维度与闵式距离值成反比关系。由此建立以下决策函数。

根据式(10)中决策函数值f(n)的大小决定最终维度，取决策函数值f(n)最小时的n作为最终维度。

电池的充电电压属性经改进的Douglas-Peucker算法压缩后的决策函数值变化如图7所示。

图7 充电电压属性不同维度的决策值Fig.7 Decision values of different dimensions of charging voltage attribute

由图7 可知，当电压属性压缩成4 维时决策值最低，随着维度提高，决策值总体变高。

利用Douglas-Peucker算法融合闵式距离模型提取充电实验的电压、电流、功率，放电实验的电压、电流和功率在各循环中的特征，最终得到34维输入特征。

4 基于二进制DBSO算法的健康因子选择

由于某些无关特征导致模型复杂度增加，模型诊断效果不佳，因此采用二进制优化算法对特征进行筛选，剔除无关特征，得到最优特征子集。

本文采用DBSO算法作为优化算法构建二进制DBSO算法对数据集进行特征选择。

自变量的定义：设置一列长度为N(N=34)的0/1二进制列向量作为优化算法的自变量，N为原始数据集中的特征个数，0是不被选择的特征，而1是被选择的特征。

首先将数据集A 的前80 个循环划分为训练样本和第81～100个循环划分为验证样本。其次建立适应度函数，以SVM 作为预测模型，以训练样本对SVM模型进行训练，用训练完的SVM模型对验证样本进行预测，以预测值与验证样本的实际值的MSE值作为适应度函数值。最后以长度为N的0/1二进制列向量作为自变量，以上述MSE 值作为适应度函数值，以DBSO算法作为优化算法，构建二进制DBSO优化算法寻找最优特征子集。

二进制DBSO 优化算法的适应度函数曲线如图8所示。

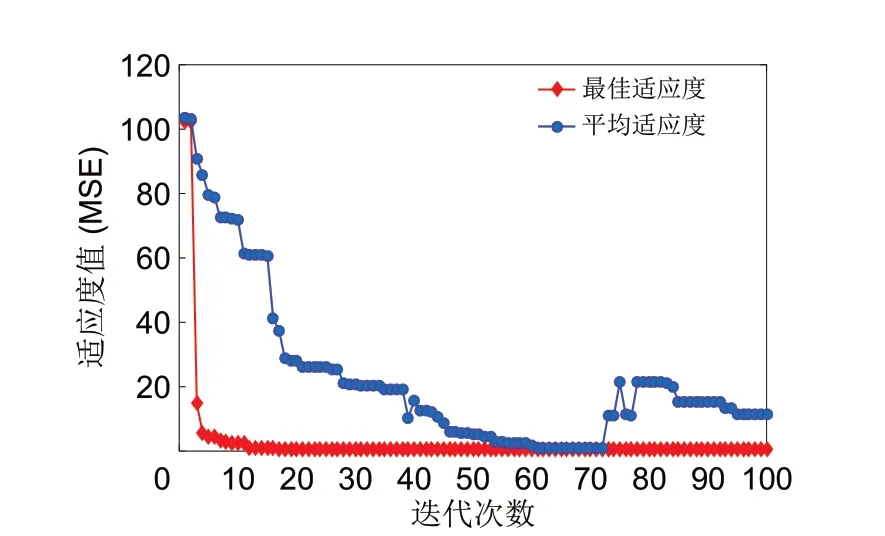
图8 DBSO优化算法的适应度曲线Fig.8 The fitness curve of DBSO optimization algorithm

由图8可知，当迭代次数达到18次后适应度函数值不再变化，MSE值达到0.587。经DBSO编码后得到7维最优特征子集。

最优特征子集之间的皮尔逊相关系数如图9所示。

图9 最优特征之间的皮尔逊相关系数图Fig.9 Pearson correlation coefficient diagram between optimal features

5 模型建立及验证

5.1 不同优化算法对SVM模型的影响

由于SVM 模型的参数对模型影响显著，因此利用DBSO 算法(差分变异的头脑风暴算法)优化SVM 的惩罚因子c和核函数参数g，并将结果与BSO 算法(头脑风暴算法)、ABC 算法(人工蜂群)相比较。DBSO、BSO、ABC算法的种群大小设置为50，迭代次数设置为100。将数据集A 的前100 个循环划分为训练样本和验证集，第101～197 个循环划分为测试样本，将验证集的MSE 值作为适应度值，各算法的适应度曲线如图10所示。

由图10 可知，DBSO 算法的MSE 值最低，寻优效果最好。ABC 算法的MSE 值最高，全局搜索能力较弱。因此表明DBSO算法比另外2种算法有着更强的局部搜索能力和全局搜索能力。

图10 不同算法优化SVM模型的迭代曲线图Fig.10 lterative curves of SVM model optimized by different algorithms

利用DBSO-SVM 模型对测试集的数据进行预测，将DBSO-SVM 模型的诊断结果与ABC-SVM模型、BSO-SVM 模型的预测结果进行对比分析，总的预测结果如图11 所示，经优化后的SVM 比原始SVM预测效果好，详细结果见表2。

图11 各类算法的预测结果图Fig.11 Prediction results of various algorithms

表2 各类算法的预测结果Table 2 Prediction results for various algorithms

由表2 可知，DBSO-SVM 模型的预测效果最好，相关系数最高，MSE值最低。

5.2 不同充放电策略下的效果

为验证本文所提出的特征工程对不同充放电策略下的锂离子电池的应用效果，本文选取数据集B对本文所建立的特征工程进行验证。

本文用误差平方和(square sum of error，SSE)、平均绝对误差(root mean square error，RMSE)、拟合优度(goodness of fit，R2)、剩余寿命的绝对误差(absolute error，AE)四个指标来评估模型性能。

经过处理得到B0005、B0006、B0007 电池的168 个循环数据，B0018 电池的131 个循环数据，将B0005、B0006、B0007的前70个循环作为训练集，70～85 循环设置为验证集，以86 循环设置为预测起点。B0018电池的前60个循环作为训练集，61～75 循环设为验证集，将76 循环设置为预测起点。根据文献[22]和文献[23]，B0005、B0006、B0007 和B0018 四块电池寿命失效阈值分别设为1.38 Ah、1.38 Ah、1.5 Ah、1.4 Ah[22-23]。利用上述建立的模型，对数据集B建立特征工程，并利用DBSO-SVM 模型对数据集B进行预测，设置各优化算法的种群大小50，迭代次数100。其结果如图12所示，经优化后的SVM比原始SVM预测效果好，详细结果见表3。

结合图12和表3所示，本文所建立的特征工程并结合DBSO-SVM 模型对数据集B取得很好的预测效果。B0005 的预测效果最好，R2达到0.99，RMSE 值低于0.002，SSE 值低于0.0002。由于B0018 号电池的容量跳跃性较大、所测循环数较少，导致B0018 电池预测效果最差。电池B0005、B0006、B0007、B0018的AE均为0，由此说明本文所建立的特征工程在SVM 模型中能准确预测电池失效，经DBSO算法优化后模型性能最佳。

图12 不同充放电策略下的预测Fig.12 Prediction diagrams under different charge and discharge strategies

表3 不同充放电策略下的各类算法的详细预测结果Table 3 Detailed prediction table of various algorithms under different charge and discharge strategies

6 结 论

为解决锂离子电池的特征工程建立困难，健康因子提取困难而导致电池的SOH 及RUL 预测效果差的问题。本文利用新威电池测试仪得到恒温条件下的实验数据，并利用所测的实验数据建立特征工程，提出新型的锂离子特征提取算法并进行了测试，结论如下：

（1）利用Douglas-Peucker算法提取健康因子时，若所提取的维度较大，容易产生特征提取位置不一致的现象，建立以闵式距离为评价指标后，可解决该问题。

（2）以Douglas-Peucker算法融合闵式距离建立的特征工程，级联二进制编码DBSO算法剔除无关特征后，验证集上的MSE值达到0.587。

（3）根据所建立的特征工程，在本文的实验数据中DBSO-SVM 模型的预测效果最好，R2达到0.987，MSE值低于3。

（4）在不同充放电策略下，本文所建立的特征工程依然取得了很好的预测效果。在数据集B中，利用DBSO-SVM 模型预测电池的RUL，电池B0005、B0006、B0007、B0018 的AE 均 为0，DBSO-SVM模型的预测效果最佳。