基于邻域搜索粒子群算法的节点定位算法研究*

刘芷珺，张玲华

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京邮电大学 江苏省通信与网络技术工程研究中心，江苏 南京 210023)

0 引言

无线传感器网络(Wireless Sensor Networks,WSNs)中有大量的传感器节点[1]，对于大多数WSNs 应用，如果节点收集到的数据信息没有结合位置信息，那么这个信息的可用度将大大降低。因此，准确知晓节点的物理位置是WSNs 应用的关键，传感器节点的定位技术是WSNs 的一个重要技术[2]。目前无线传感器网络的定位算法通常分为两大类：基于测距的定位算法(Range-based Algorithm)[3-6]和无需测距的定位算法(Range-free Algorithm)[7-10]。基于测距的定位算法与无需测距的定位算法相比，前者的性能通常要优于后者，但前者需要投入大量的成本且对硬件要求很高；后者能耗低、实现成本低、不需要硬件支持，同时又可以满足许多应用需求[11]。因此，无需测距的定位算法有着更加重要的研究意义。

DV-Hop 定位算法之所以可以得到非常广泛的应用，离不开其步骤简单、容易实现并且定位覆盖面积大等优点，但是作为经典的无需测距定位算法，它的缺点也非常显著，即受网络拓扑影响大，定位误差较大。针对DV-Hop 定位误差大这个问题，已经有很多学者提出了自己的改进措施：文献[12]利用节点接收的信号强度值对跳数进行修正从而获得更加精确的节点坐标；文献[13]构建测距误差代价函数，并利用无偏估计对跳距进行校正；文献[14]将DV-Hop 算法的定位结果作为斯蒂芬森迭代模型的初始值，最后通过斯蒂芬森不断迭代得到最优的节点位置；还有文献引入智能优化算法(如狼群优化算法[15]、粒子群优化算法[16]、模拟退火算法[17]、遗传算法[18]）来实现对DV-Hop 算法的改进。然而，这些算法虽然针对经典的DV-Hop 算法进行改进，但是改进后的定位精度仍然不是很高。尤其像遗传算法、狼群优化算法这种计算量较大的优化算法会大大增加节点的通信负担。

粒子群优化算法具有实现简单、参数少、计算量小等特点，因此在大量智能优化算法中脱颖而出，得到了广泛应用。本文在粒子群优化算法的基础上增添了邻域搜索算法，进而将改进后的邻域搜索粒子群优化算法应用于DV-Hop 定位算法来估计未知节点的位置，同时在充分分析DV-Hop 算法的不足后，对传统DV-Hop 算法中的跳数和平均跳距进行修正改进，最终设计出IDVHop-NSPSO 算法。

1 DV-Hop 算法及误差分析

1.1 DV-Hop 算法

DV-Hop 定位算法最初是由Dragos Niculescu 教授等人提出的[4]。该算法分为三个阶段。

第一阶段：计算节点间的最小跳数。利用泛洪的方式使监测区域内所有节点接收到各信标节点的位置信息和距离各信标节点的最小跳数[19]。

第二阶段：计算信标节点的平均跳距并估算未知节点到信标节点的距离。由式(1)计算得到每一个信标节点的平均跳距：

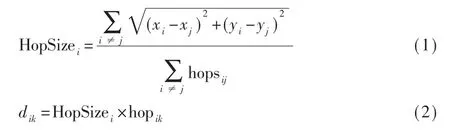
信标节点间的距离与信标节点间的跳数相除即可得到各信标节点的平均跳距；再利用式(2)求得未知节点到信标节点的估算距离，信标节点i 为距离未知节点k最近的信标节点。

第三阶段：计算未知节点位置。第三阶段通常采用最小二乘法或三边测量法计算未知节点位置，本文采用最小二乘法。设di(1≤i≤n，n 为信标节点总数)为未知节点与各信标节点(xi，yi)的距离，则:

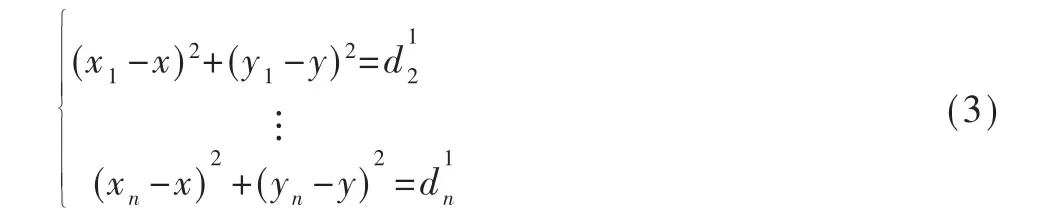
把式(3)改写为AX=b 的形式，其中A、b、X 具体如式(4)～式(6)所示：

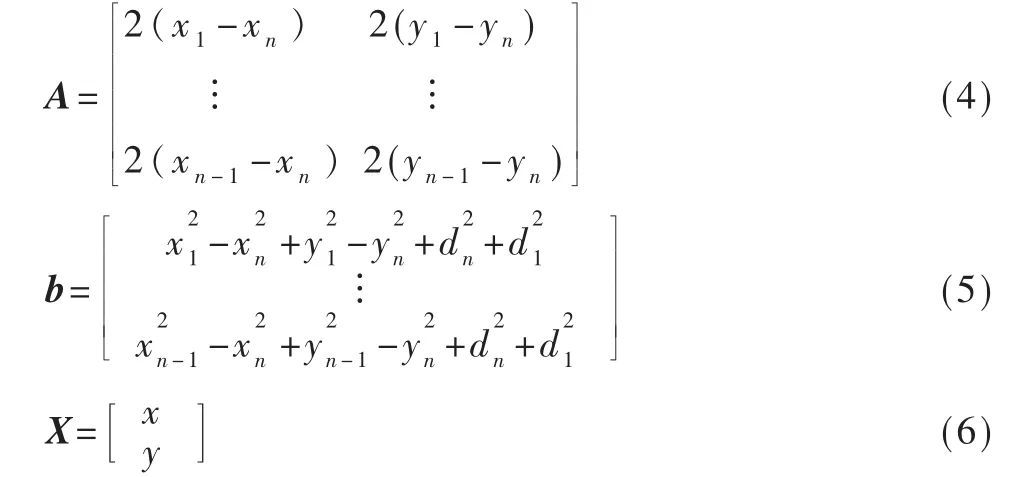
利用式(7)解之可得未知节点的位置：

1.2 误差分析

（1）最小跳数

在计算最小跳数时，传统的DV-Hop 算法将信标节点通信范围内的节点均视为一跳，如图1 所示，点B 与点C 均存在于点A 的通信范围内，但是点B 与点A、点C 与点A 的距离却相去甚远，这时若都视为一跳则误差较大。

图1 一跳距离示意图

（2）未知节点采用的平均跳距

在DV-Hop 算法的第二阶段中的式（2）里，HopSizei即为未知节点k 采用的平均跳距，这个平均跳距是距离该未知节点k 最近的信标节点i 的平均跳距。但实际上，距离未知节点最近的信标节点的平均跳距并不能代表监测范围内其他信标节点的分布状况，更不能代表该未知节点自己的平均跳距，并且由于DV-Hop 定位算法利用多跳代替直线距离，未知节点距离信标节点的跳数越大，误差就会越明显。

（3）最小二乘法或三边测量法

传统的DV-Hop 算法在第三阶段常采用最小二乘法或三边测量法计算未知节点位置，但这两种方法也有很明显的弊端，如果出现式(7)中的矩阵ATA 的逆不存在的情况，或者是节点共线时，将无法使用这两种方法计算。

2 优化改进后的DV-Hop 算法

2.1 最小跳数修正和加权平均跳距

针对1.2 节中最小跳数误差原因，本文在计算最小跳数时增设了半跳。在WSNs 中，信标节点通过广播使其他未知节点得到数据包，未知节点在收到数据包时会有一个接收信号的强度，强度大表示未知节点与信标节点的距离近，反之则远。基于此原理，利用未知节点接收信号强度来细化每一跳，增设一个功率阈值W，低于此阈值视为半跳即0.5 跳，高于此阈值则视为一跳，阈值W 为传播距离为R/2 时的接收信号强度(R 为节点最大通信半径)。

针对1.2 节中未知节点采用的平均跳距误差原因分析，由于距离未知节点最近的信标节点的平均跳距并不能代表该未知节点的平均跳距，由此引入权重系数和多个信标节点的平均跳距，距离未知节点近的信标节点带来的平均跳距更加贴近实际，则权重大；距离未知节点远的信标节点可能会带来较大误差，因此权重就小。总之就是弱化带来较大误差影响的信标节点的作用，权重系数如式(8)[20]所示：

其中，hi为未知节点到信标节点i 的跳数。如此，未知节点的加权平均跳距则为式(9):

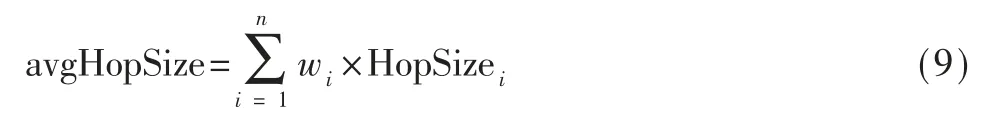
利用式（9）可求得更加精确的距离，从而估算出未知节点坐标。

2.2 采用邻域搜索粒子群优化算法计算未知节点位置

2.2.1 传统粒子群优化算法

粒子群优化算法 (Particle Wwarm Optimization，PSO)由Eberhart 和Kennedy 于1995年提出[21]。粒子群优化算法拥有一个群体，该群体中的每一个粒子都拥有自己的初始位置和初始速度，群体中的所有粒子都在搜寻最优解，但由于所有粒子都未知最优解所在位置，最好的办法就是在距离最优解最近的粒子附近搜索。于是粒子根据既往的经验和群体行为进行演化、修正，通过式(10)和式(11)更新自己的位置和速度，直到达到最大迭代次数或满足一定的误差后，停止搜索，得到最优解[22]。

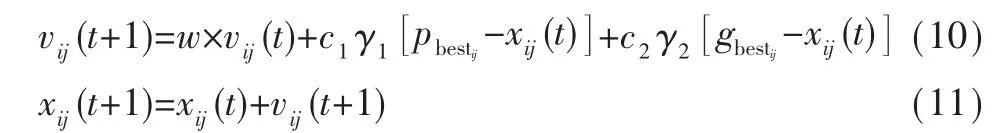
其中，在算法优化过程中，会形成局部最优解pbestij和全局最优解gbestij；vij(t)为粒子的速度；w为惯性权重；c1和c2为学习因子；γ1、γ2为[0,1]之间的随机数；xij(t)为粒子的位置；t为迭代次数。

2.2.2 邻域搜索粒子群优化DV-Hop 算法

全局搜索能力和局部搜索能力通常可以判断一个智能优化算法的优劣，前者是指找到最优解最有可能出现区域的能力，即找到一个大致的方向区域；后者是指在这个最有可能出现最优解的区域内无限接近最优解的能力。标准的粒子群优化算法在运行前期的性能较好，收敛也比较快，但是后期容易陷入局部最优，在接近最优解的时候，收敛速度降低甚至会出现停止收敛的情况[21]，搜索算法一旦陷入局部极值点，算法就在该点处结束，这时得到的结果极有可能并不是全局最优解。为了准确得到全局最优解，提升解的质量，本文加入一种局部搜索算法——邻域搜索算法。在邻域搜索过程中粒子首先会使用已经得到的最优解作为初始解，在这个初始解的邻域中继续搜索其他候选解，并将当前的最优解与其他候选解按照某种特定的规则进行对比取优重新确定当前新的最优解状态。重复上述操作，直到满足提前设定的条件，算法终止，得到最优解。在邻域搜索算法中，粒子总会选择表现更优的邻域更新状态，持续地寻找比当前解表现更好的解。邻域搜索算法的加入大大提升了算法在局部搜索时的寻优精度和成功率。

本文在粒子群优化算法的基础上增加邻域搜索策略，使粒子群优化算法在进行局部搜索时更加细致准确定位最优解位置。每个粒子产生一个初始最优位置，之后利用式(10)和式(11)更新粒子的速度和位置，若新生成的解比历史最优解的表现好，则以新生成的解为中心，在以新生成的解和历史最优解的距离为半径的位置上多次搜寻，搜寻到的点作为反向点，在反向点的位置再进行搜索；若新生成的解比历史最优解的表现差，则以历史最优解为中心生成反向点，再进行搜索。最终将搜索的结果与历史最优解进行比较，若更优则采纳，否则遗弃。综上所述，邻域搜索算法中邻域动作根据新生成的解与历史最优解的表现（自适应函数值）来确定，通过以不同圆心作不同半径圆的邻域动作产生反向点；判断反向点的质量和选择反向点的策略则是利用粒子的自适应度函数值来确定的。

粒子群优化算法中的惯性权重w 的作用也举足轻重，通过式(10)可以看到惯性权重的大小与粒子的速度息息相关，惯性权重大则粒子速度快，这也意味着粒子可以用更大的步长来搜寻最优解，全局搜索能力强；惯性权重小则粒子速度慢，粒子的步长就小，可以更加精细地局部搜索最优解。然而惯性权重过大或者过小都会对粒子群优化算法带来负面的影响：过大会导致算法过早收敛，形成“早熟收敛”现象；过小则会使算法陷入局部最优。因此，本文采用典型线性递减策略[23]，如式(12)所示。迭代初期惯性权重大，从而粒子速度比较大，全局搜索能力强；随着迭代次数的增大，惯性权重变小，粒子速度也随之变小，全局搜索能力变弱，局部搜索能力变强。

其中，wmax、wmin分别为惯性权重的最大值和最小值；t 为当前迭代次数；tmax为最大迭代次数。

本文对于粒子群优化算法的修改相较于传统粒子群优化算法不仅提高了算法的收敛速度，并且改善了种群容易陷入局部最优的缺点，增强了粒子群优化算法的全局搜索能力。

2.2.3 改进后的IDVHop-NSPSO 算法步骤

IDVHop-NSPSO 算法的具体步骤如下：

（1）随机部署传感器节点，计算修正后的最小跳数hop，利用式(9)计算出未知节点与信标节点之间的加权估算距离d；

（2）初始化粒子群的群体规模、每个粒子的初始位置x、速度v、个体最优值pbest及全局最优值gbest；

（3）利用式(13)计算每个粒子的适应度函数：

（6）达到最大迭代次数退出，否则返回步骤（4）。

3 仿真实验结果

本文采用MATLAB R2017a 仿真平台对本文改进的算法进行仿真，并与传统的DV-Hop 算法、文献[16]提出的DV-Hop+PSO 算法和文献[17]提出的模拟退火加权DV-Hop 算法进行对比。实验环境设置如下：仿真区域大小为100 m×100 m，随机放置100 个节点。利用控制变量法分别观察信标节点个数、节点最大通信半径、总节点个数对于定位误差的影响。采用式(18)节点平均误差error 作为本次算法结果的评价标准，节点平均误差值越小说明定位精度越高。

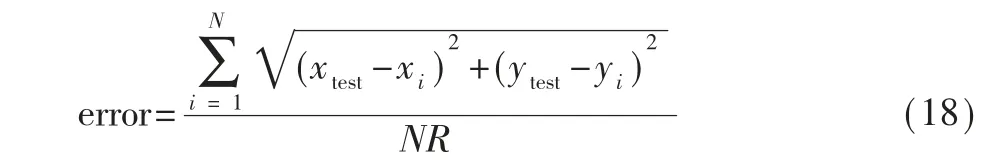
其中，(xi,yi)为未知节点的实际坐标，(xtest,ytest)为计算出的未知节点估计坐标，N 为未知节点的个数，R 为信标节点的最大通信半径。为保证算法的稳定性与可靠性，每种算法均循环50 次后求取平均值进行比较。

在仿真实验中，本文采用缩写dv 代表DV-Hop 算法，dvsa 代表模拟退火加权DV-Hop 算法，dvpso 代表DV-Hop+PSO 算法，idvpso2代表本文提出的IDVHop-NSPSO 算法。

（1）不同信标节点数对定位的影响

仿真参数见表1，不同信标节点数对定位影响如图2 所示。随着信标节点数量的增加，定位的平均误差不断减小。但在信标节点个数小于7 时，本文提出的IDVHop-NSPSO 算法精度没有模拟退火加权算法精度高。将本文提出的IDVHop-NSPSO 算法与DV-Hop 算法、DV-Hop+PSO 算法、模拟退火加权算法进行对比，定位精度分别提升约30.9%、18.2%、13.1%，定位精度得到明显提升。

表1 信标节点可变时的仿真参数

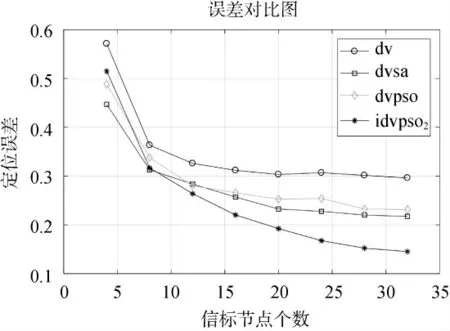
图2 定位误差与信标节点关系图

（2）不同通信半径对定位的影响

仿真参数见表2，不同通信半径对定位的影响如图3 所示，随着节点通信半径的增大，定位精度不断增强，同时可以从图中看出，当通信半径在小于46 m 时，DVHop 算法的精度要比DV-Hop+PSO 算法的精度高，本文提出的IDVHop-NSPSO 算法的精度在图中所示所有通信半径范围内比两者都要高，分别高出约18.4%、42.5%，定位精度得到明显提升；但本文提出的算法与文献[17]提出的模拟退火加权DV-Hop 算法精度相差不多，且在通信节点大于25 m 后，定位误差降低的趋势明显放缓。

图3 定位误差与节点通信半径关系图

表2 最大通信半径可变时的仿真参数

（3）不同总节点数量对定位的影响

仿真参数见表3，不同总节点数量对定位的影响如图4 所示，可以看出，随着总节点个数的增大，未知节点的定位误差也呈上升趋势，本文提出的IDVHop-NSPSO比DV-Hop算法、DV-Hop+PSO算法、模拟退火加权DV-Hop 算法精度都要高，分别高出约16.25%、8.61%、2.3%，定位精度得到提升。

表3 总节点数可变时的仿真参数

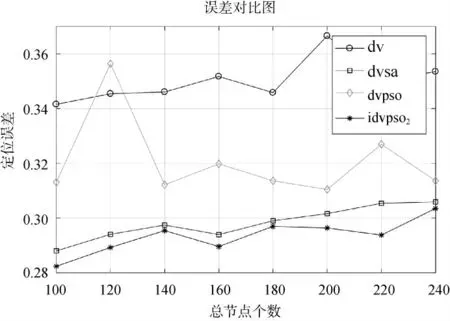
图4 定位误差与总节点个数关系图

（4）时间复杂度

在无线传感器网络定位算法中，由于节点能源有限，算法的复杂度也成为评判算法优良的一项重要指标。现假设监测区域内总节点数为n，未知节点数为m，PSO 算法、模拟退火算法和本文应用的NSPSO 算法的迭代次数为T，空间维度为D，种群数目为N，其中N＞＞D，经过计算后，4 种算法各个阶段的时间复杂度如表4 所示。

表4 比较4 种算法各阶段的时间复杂度

从表4 中可以看出,DV-Hop 算法的时间复杂度为O(n3)+O(n)+O(m)，DV-Hop+PSO 算法的时间复杂度为O(n3)+O(n)+6×O(m×T×N)，模拟退火加权DV-Hop算法的时间复杂度为O(n3)+O(n)+12×O(m×T×N)，IDVHop-NSPSO算法的时间复杂度为O(n3)+O(n)+10×O(m×T×N)，本算法的时间复杂度虽略高于DV-Hop 算法、DV-Hop+PSO 算法，但是比文献[17]提出的模拟退火加权DV-Hop 算法低。

4 结论

针对DV-Hop 算法定位精度不高、DV-Hop+PSO 算法精度不够高且效果不稳定、模拟退火加权DV-Hop 算法耗时复杂等不足，本文提出了IDVHop-NSPSO 算法。首先在计算最小跳数时增设半跳细化最小跳数；然后在计算未知节点平均跳距时引入权重系数和多个信标节点的平均跳距，求得的加权平均跳距使未知节点采用的平均跳距更加精确，从而使求得的估算距离更加贴近实际距离；最后，在计算未知节点位置阶段，利用邻域搜索粒子群优化算法替代最小二乘法将定位问题转换为寻优问题进行求解，定位精度得到了较高的提升且效果稳定。通过实验结果可以看出，相较于传统的DV-Hop 算法和DV-Hop+PSO 算法，本文提出的IDVHop-NSPSO 算法的定位精度得到了很大的提升；相较于模拟退火加权DV-Hop 算法，本文提出的IDVHop-NSPSO 算法的计算量变小，节点耗能变少且精度也得到了一定提升。但是由于邻域搜索PSO 算法的引入，不可避免地增加了一些计算开销，这也是后期研究优化的方向。