基于动力学演化样本的代理模型优化方法
胡钊晖,邓琎,李再参,吴锋,b,钟万勰,b
(1.大连理工大学 工程力学系,辽宁 大连 116024;2.云南省机械研究设计院有限公司 a.云南省机电一体化应用技术重点实验室;b.钟万勰院士工作站,昆明 650031)
0 引 言
在工业装备结构优化设计时,直接利用有限元仿真难以达到高效、快速设计的要求,利用代理模型进行高效优化是当下的研究热点之一。在利用代理模型进行优化时,为在设计空间中建立全局高精度代理模型,采样方法尤为重要。随机采样方法得到的样本点集分布极不均匀,所构造的代理模型的精度很差。目前,学者大多采用均匀性分布较好的样本点集,如拉丁超立方抽样,以及基于数论理论的Hammersely点集、Sobol点集和Halton点集等。然而,这些点集存在明显缺点:高维点集在低维投影时,投影点常出现聚集现象,分布不再均匀。样本的均匀性对代理模型的精度具有显著影响,采用均匀性好的样本点集,往往可以用很少的样本数得到精度更好的代理模型,从而实现更高效的优化设计。
实际上,均匀性好的样本点集在优化设计、随机模拟、试验设计等诸多问题中都有重要的应用价值,如何生成均匀性更好的样本点集一直是研究热点。文献[5]将点集模拟为星系的动力学演化,并证明“最小距离最大化”原则等价于力学分析中的最小势能原理。基于最小势能原理,文献[5]提出一种基于动力学演化模型优化的采样方法。相较于其他点集,动力演化点集的均匀性更好,可以为构造高精度代理模型和优化设计提供均匀样本,已经成功用于随机问题分析。然而,动力学演化样本生成方法是否适用于代理模型和优化设计,还值得进一步研究。
本文将动力学演化样本生成方法引入到代理模型优化设计中,通过拉丁超立方抽样得到初始样本点集,基于动力学演化计算生成均匀性更好的样本点集,并用于代理模型的构造,采用遗传算法得到最优解,从而给出一套基于动力学演化的代理模型优化方法。通过经典测试函数和某实际机床的优化分析,研究所提出的基于动力学演化的代理模型优化方法的性能。
1 基于动力学演化样本的代理模型优化
1.1 代理模型优化
基于代理模型优化方法的计算步骤通常为:(1)在设计变量空间选取样本;(2)基于各样本,采用有限元仿真计算得到响应值;(3)根据样本和响应值,生成代理模型;(4)采用优化算法寻找代理模型的最优解。在这4个基本步骤中,影响优化结果的主要因素有3个,即样本、代理模型和优化算法,本文代理模型和优化算法分别选择经典的Kriging模型和遗传算法,主要研究样本生成。
结合动力学演化方法生成样本:首先基于拉丁超立方采样生成初始样本,然后基于动力学演化方法对该样本进行优化,得到更为均匀的样本分布,以期提高代理模型的精度,进而提高优化结果。
1.2 动力学演化方法
假设采样空间为立方体=[0,1],其中样本点集为,={,,…,},每个点视为一个质量为的星体,点与点之间存在相互作用力,整个点集的作用量和Lagrange函数为
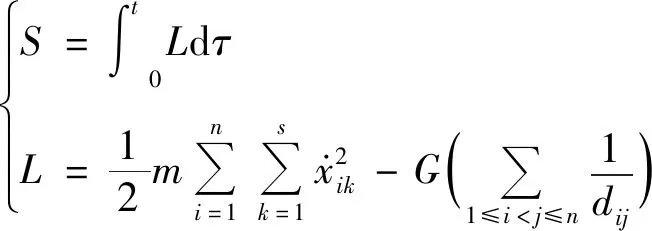
(1)
式中:为引力常数;为点与点之间的欧氏距离。
根据Hamilton变分原理可得

(2)
其中:

(3)
为追求静态解,可给每个星体施加一个人为的阻尼力,于是式(2)可表示为

(4)

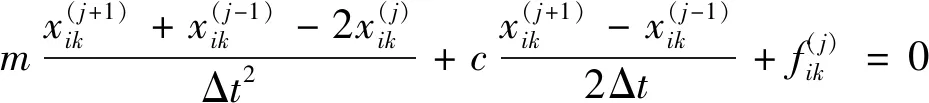
(5)
式中:上标()中的表示在时间=×Δ处的值。
整理式(5)得

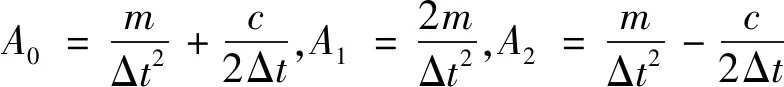
(6)
式(6)演化迭代过程中涉及的演化参数选择和点出界处理等,均可参考文献[5]的相应说明。此处以拉丁超立方抽样方法生成100个二维样本点集,其样本点分布见图1(a)。以该样本点集为初始点集,假定初始速度为0,根据式(5)进行演化计算,最终得到势能最小的样本点集,其分布见图1(b)。演化后的点集要比演化前的点集均匀得多。

(a)拉丁超立方点集
2 测试算例
为方便论述,将基于拉丁超立方抽样的Kriging代理模型简记为LK模型,将基于动力学演化技术对拉丁超立方样本进行优化并构建的Kriging代理模型简记为DLK模型。
2.1 数学函数测试
选择二维情况下优化测试常用的4个解析数学函数(见式(7)),比较拉丁超立方点集及其演化点集在构建代理模型时的精度,并结合遗传算法,对比代理模型全局最优解与函数全局最优解的精度。
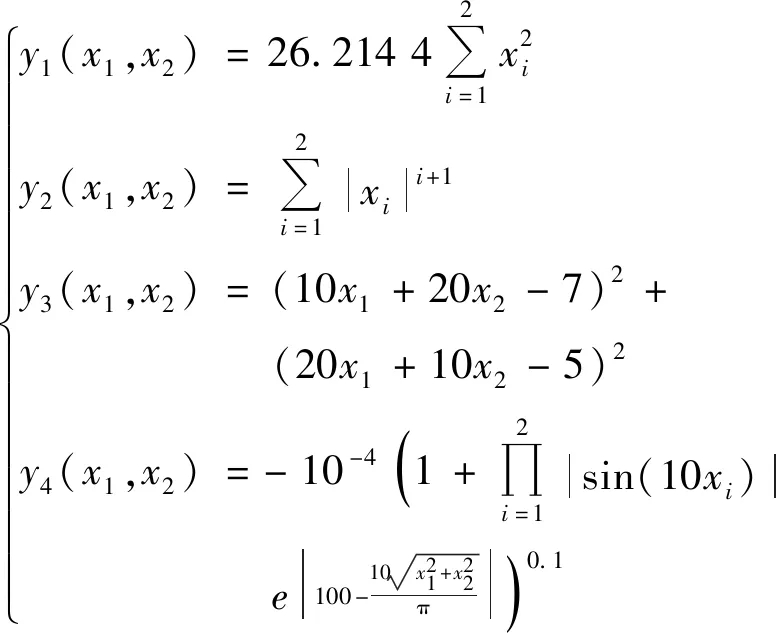
(7)
为比较演化前、后代理模型的精度,上述4个函数的样本数均选100。为测试所构建的LK模型和DLK模型的精度,在优化变量定义域内随机生成200个点集,将均方根误差和相对平均绝对误差作为误差评判标准,其定义分别为

(8)
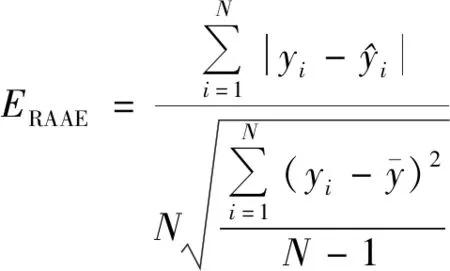
(9)

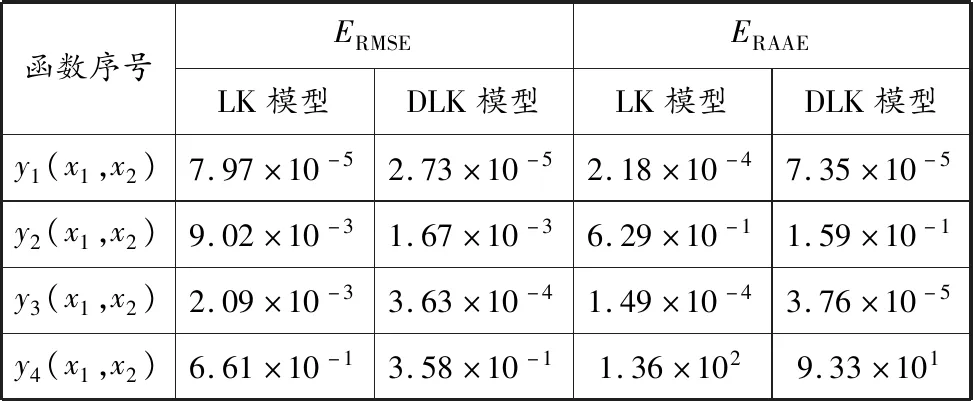
表 1 点集的误差计算结果
由表1可知,对于均方根误差和相对平均误差而言,DLK模型的结果均显著好于LK模型的结果。这表明,经过动力学演化后的样本可以显著提高Kriging代理模型的精度。
采用遗传算法对得到的LK模型和DLK模型进行全局寻优,得到的结果见表2。
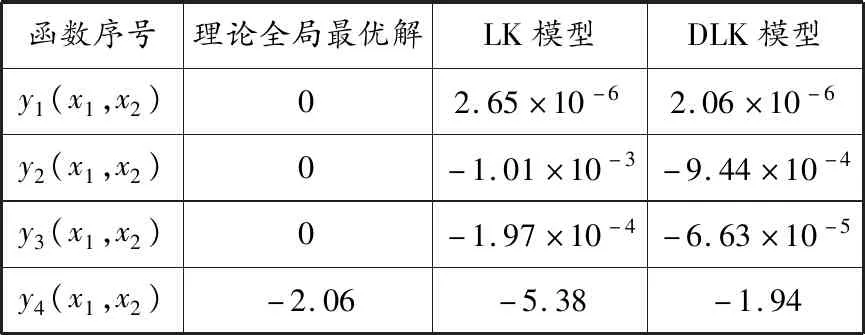
表 2 测试函数优化结果对比
由表2可知,对于所研究的4个测试函数,DLK模型的优化精度均好于LK模型的优化精度,其中在函数上表现得尤为明显。因此,使用动力学演化的样本不仅能构建精度更好的代理模型,而且在寻找全局最优解方面也更为有效。
2.2 机床横梁优化实例
选用某龙门铣床横梁,其结构模型见图2。横梁材料为HT250铸铁,密度为=7 200 kg/m,弹性模量=66.2 GPa,泊松比=0.27。机床横梁需要与立柱滑块等进行装配,外部尺寸无法作为设计变量,因此将结构上3个孔洞尺寸作为设计变量,分别为顶部圆孔直径80 mm≤≤160 mm,背部圆角正方形孔洞边长425 mm≤≤485 mm和侧面圆角矩形孔洞长度220 mm≤≤280 mm。优化目标为在使得横梁最大应力尽可能小的情况下提升机床横梁的整体刚度。
采用10个样本,分别生成该横梁最大应力的LK和DLK计算模型,并采用遗传算法进行全局优化,优化后得到3个变量的最优值,将之代入有限元软件,计算得到最大应力值。2个模型的计算结果对比见表3。DLK模型优化得到的最大应力明显小于LK模型优化得到的最大应力,再次表明使用动力学演化的样本可以找到更优的设计解。
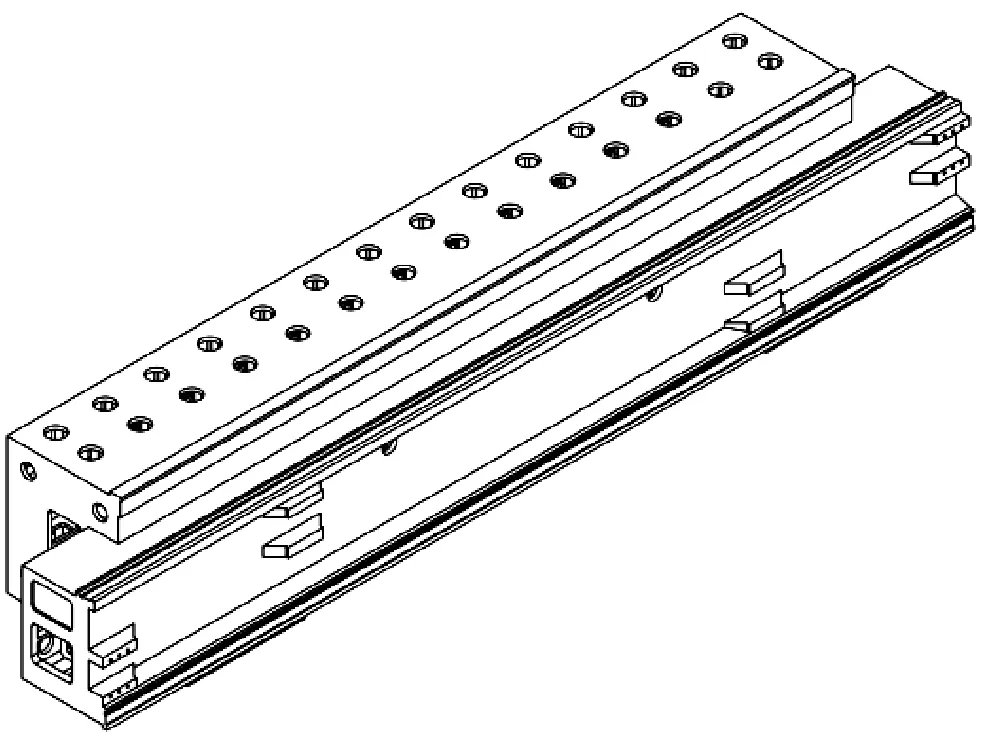
(a)等轴侧视图

表 3 LK模型与DLK模型的优化结果对比
3 结束语
首先,将动力学演化样本生成方法引入代理模型优化设计,通过拉丁超立方抽样得到初始样本点集;然后,基于动力学演化计算,生成更均匀的样本点集,并用于代理模型构造;最后,基于遗传算法得到最优解,从而给出一套基于动力学演化的代理模型优化方法。通过函数测试和机床横梁优化实例,证明演化后样本集在代理模型构建和模型全局寻优方面的优越性。

