功能神经元建模及动力学若干问题

马 军

(兰州理工大学 理学院， 甘肃 兰州 730050)

神经系统包含巨量的神经元，这些神经元在发育中逐渐强化了某种特殊感知功能，因而在脑皮层形成不同功能区。单一神经元在受到邻近神经元或者外部刺激后可以诱发多样放电模态，如呈现静息态、尖峰放电、簇放电以及混沌放电，这表达了神经元的应激反应能力[1-5]。实际的神经元具有复杂解剖结构，其胞体内的钙离子、钾离子、钠离子和氯离子受到细胞膜的约束，其树突分布有利于从多个方位感知刺激信号，细胞膜内离子浓度改变和膜片通道蛋白的激活对离子输运有重要的调控作用。生物神经元受到刺激后，细胞膜内外离子浓度发生突变而触发动作电位，这种电生理信号沿着轴突传递到突触前端，进一步被邻近神经元的突触后端捕获和感知，实现神经元之间信号的传递和编码。实验发现，一些中间神经元具有自突触结构[6-8]，即突触经过一定的绕行回路再次连接到胞体树突，其物理机理是神经元轴突受损而发育形成的辅助回路[9]，达到对信号修复目的，另一方面，自突触的激活也体现了神经元自适应性，使得神经元对外界刺激的响应模态具有选择性[10]。从物理角度看，任何一个神经元都可以看作一个复杂的带电体，其静态的带电离子可以诱发静态的电场，而离子在细胞内的输运及跨膜流动会诱发磁场，因此，任何一个神经元都处于其他神经元诱发的电磁场中，神经元之间建立一定的突触连接来实现彼此的能量平衡，从而神经元可以处于不同的放电模态。从实际生理环境来看，神经元受到的刺激可以来自邻近的神经元，也可能是直接的外部恒定的电信号、周期的电信号，或者噪声类型的随机刺激，也可以是电磁场极化效应产生的感应电流。Hodgkin-Huxley的生物神经元模型[11-12]为理论生物神经科学和计算神经科学提供了重要起点，忽略离子通道效应后的Hindmarsh-Rose神经元模型[13-14]为简化计算和细致的非线性分析提供了便利。神经元在多重刺激下可以诱发相干共振或随机共振，其膜电位序列在特定噪声强度下呈现高度有序性和相关性。当这些特殊的神经元模型被用于构建不同拓扑结构的神经元网络后，其耦合通道的属性、连接方式、边界条件及噪声都会对神经元网络群体电活动模态产生显著影响。特别地，在恰当的耦合方式和噪声驱动下，神经元网络内因为自组织会诱发出多样性的时空斑图，或者被控制后达到不同程度的网络同步[15-18]。

从实验角度探索神经系统电活动诱发模态机理和神经元之间的协作具有一定程度的困难。考虑到实际的生物神经元具有很强的自适应性，对信号处理具有很高的智能性。因此，一些研究人员提出构造各种非线性电路，对这些非线性电路的参数进行调制或施加外部刺激，当这些非线性电路的电压输出序列能呈现类似生物神经元那样尖峰放电、簇放电和混沌放电特征时，那么这些非线性电路就可以当作神经元电路来使用[19-24]。特别地，对这些神经元电路嵌入特殊的功能性器件，如压电陶瓷、光电管、热敏电阻等，那么这些改进的神经元电路就可以感知外界特殊的物理信号。进一步对这些特殊的神经元电路方程进行标度变换，就可以得到各类无量纲的功能性神经元模型，如热敏神经元、光敏神经元和听觉神经元[25-29]。这些不同的功能神经元组建各种神经元网络就可以表达不同功能区的协作和信号交互问题。从物理角度看，在神经元之间通信的过程必然伴随着能量的输运和交互，定量化计算每个神经元及其耦合通道的能量，对耦合通道的功能进行强化，就可以增强人工神经元网络的功能和智能化。

1 广义神经元电路的基本特征

实际的生物神经元包含静态电场和动态磁场效应，在外界刺激下能产生多种放电模态是因为介质的非线性效应。电容器在充电和放电过程中会诱发电场，同时存储和释放电场能量；电感线圈中的电流变化时伴随着磁场的改变会诱发感应电动势，同时存储和释放磁场能量。非线性电阻如隧道二极管的伏安曲线呈现非线性特征，在电路中对电容器输出电压和感应线圈的电流会产生非线性调控。因此，简单的神经元电路必须包含电容器、感应线圈和非线性电阻。考虑到实际神经元的不同离子存在对应的静息态电位(反转电位)，因而在神经元电路中感应线圈所在的支路会嵌入一个恒定的电压源来表达反转电位。另一方面，只包含单一电容器、感应线圈和负电阻的神经元电路(RLC)是一个自治系统，其输出电压序列只能表现出尖峰放电、周期放电、簇放电和恒定值(静息态)。为了诱发出混沌态，通常对RLC电路施加周期性的刺激电流或者外置电压源来激励。当外界信号源是周期信号时，选择恰当的刺激幅度和频率就可以在非线性电路中诱发混沌，该混沌电路方程无量纲化后就得到一个非自治的二变量动力学系统，利用分岔分析或者计算系统的最大李雅普诺夫指数就可以确定系统产生混沌的参数区。如图1所示，一个简单的RLC神经元电路[30]在电压源驱动下其输出电压序列呈现多种放电模式。图1中C、L、NR、E和Vs分别表示电容器、感应线圈、非线性电阻、恒定电压源和时变的电压源，Rs、R表示线性电阻。

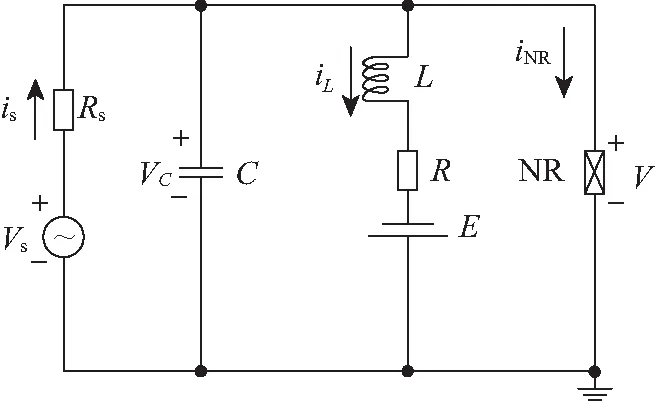
图1 神经元电路示意Fig.1 Schematic diagram for neural circuit

根据基尔霍夫定律得到图1电路的方程为：

(1)

其中通过非线性电阻NR的通道电流—电压关系为

(2)

为了进一步分析，对方程(1)和(2)的物理变量和参数进行如下标度变换:

(3)

则神经元电路方程式(1)可以等效表达为如下无量纲的振子模型:

(4)

从动力学角度看，改变外界刺激us的值会改变神经元的激发性，诱发神经元产生不同的放电模式。神经元电路里的电容器和感应线圈可以存储场能量，该能量WE和神经元模型式(4)的哈密顿能量函数H一一对应。

(5)

显然，神经元的瞬态能量和放电模态相关，外界刺激改变了放电模态，本质上是改变了神经元的能量。当非线性电路暴露于电磁场环境中，电容器的电场能量密度和感应线圈的磁场能量密度会受到随机性扰动，因此，通常用加性噪声来表达外界电磁场辐射引发的随机效应。在无量纲神经元模型中，2类不同的噪声则以不同方式来激励神经元。

(6)

式中，ηE、ηM分别表示外界电场和磁场涨落对膜电位和通道电流产生的随机性扰动，这种随机性激励可以用高斯白噪声来表达，其统计关系如下：

(7)

式中：〈*〉表示对变量进行时间平均；D、D′表示噪声强度；δ(*)表示狄拉克δ函数，定义如下:

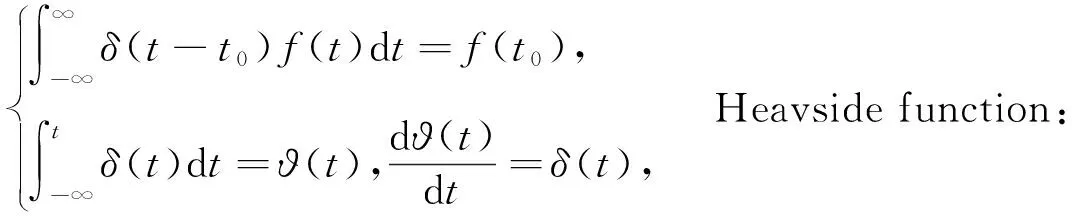
(8)

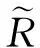
(9)

式中：h表示采样序列对应的功率谱的峰高；Δf表示峰值一半所对应的峰宽；fp表示峰所对应的频率。若SNR随着噪声强度的增大而增大，当达到一个最大值后，再随着噪声强度的减小而减小，就预示着系统在噪声的作用下产生了随机/相干共振现象。在没有周期信号激励下，CV值随着噪声强度增加而减小，当达到一个最小值后，随着噪声强度的增加而增加，这预示着神经元在噪声作用下诱发了相干共振，相干系数次数也取得极大值。从信号处理的角度看，随机共振为噪声环境下弱周期信号的检测提供了理论依据。

2 非线性电路场能量及动力学系统哈密顿能量

当电容器和感应线圈嵌入到电路中，各个支路电流的变化引起电容器内电场能量和线圈内磁场能量的变化，而电阻则消耗一定的焦耳热。对于一般的动力学系统而言，其变量的演化和相互关联可以在等效的非线性电路中实现，即把各个无量纲的变量和参数利用标度反变化来与电容器、感应线圈和电阻的输出变量及物理参数一一对应。赫姆霍兹定理[37]表明，任意电磁场可以分解为标量势的负梯度和矢量矢的旋度之和，其场方程表示为

F(r)=Fd(r)+Fc(r)=-∇φ(r)+∇×A(r)。

(10)

即任意场可以当作梯度场和涡旋场的叠加，且这2种场以不同方式存储场能量。静电场一般具有梯度场的特征，感应电场和磁场具有涡旋场的特征。对于一般的非线性动力学系统，按照矢量场方式也可以做类似的分解，其哈密顿能量函数H[38-39]满足赫姆霍兹定理。

(11)

式中J(X)和R(X)分别表示斜对称矩阵和主对角矩阵。以式(4)表达的神经元模型为例，其动力学方程可以等效表达为矢量场形式，

(12)

根据式(11),其哈密顿能量函数和式(5)的无量纲能量函数H完全一致。类似地，更多混沌系统的哈密顿能量函数的求解见文献[40],相关结果表明实际的物理系统的哈密顿能量函数是唯一的，对其进行动力学控制时选择李雅普诺夫函数必须与其内在的哈密顿能量函数一致，而对于广义的动力学系统，其李雅普诺夫函数的选择只要满足李雅普诺夫定理要求即可。

3 热敏神经元电路

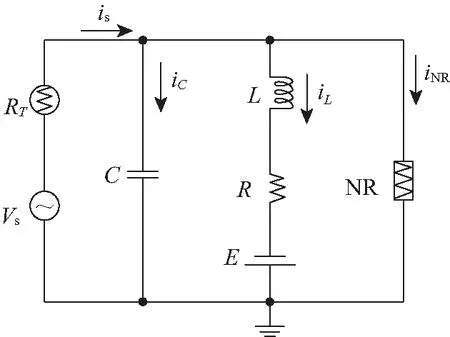
图2 热敏神经元电路示意Fig.2 Schematic diagram for a thermosensitive neural circuit

在图1的神经元电路中嵌入热敏电阻，如分别替换不同支路的线性电阻Rs、R, 随着温度的改变和热效应的积累，流经热敏电阻所在支路的电流会受到温度的影响，但温度对其动力学的影响方式不同。当热敏电阻替换掉和电压源串联的线性电阻Rs，其刺激电流就依赖于温度，进而影响其激发性和放电模态。当热敏电阻替换掉和感应线圈串联的线性电阻R,相当于神经元的离子通道电流受到温度的控制。如果同时用2个热敏电阻替换掉原来的线性电阻Rs、R，则意味着其激发性和离子通道都受到温度的调控。这里考虑负温度系数的热敏电阻(negative temperature coefficient，NTC)和周期性信号源串联的情况，随着温度的增加，NTC热敏电阻的阻值以指数形式衰减，对应的热敏神经元电路见图2。热敏电阻的阻值R=R∞exp(B/T),B=q/K,其中q表示活化能，K表示玻尔兹曼常数，R∞是该电阻在温度取无穷大时的阻值。

类似地，图2对应的热敏神经元电路方程[41]表达为:

(13)

对电路方程(13)的变量和参数进行类似的标度变换，且非线性电阻的电流iNR与式(2)一致，

(14)

对应的等效热敏神经元受到的刺激电流依赖于温度，其激发性随着温度改变而触发不同的放电模式，动力学方程表达为:

(15)

进一步把图2热敏神经元电路中和感应线圈串联的线性电阻R替换为热敏电阻，那么热敏神经元如式(15)中的参数b也就和温度相关。固定参数a=0.7,b=0.8,c=0.1,改变温度值使得外界刺激电流发生相应的改变，进而引发神经元放电模态发生迁移，其对应的哈密顿能量也随之发生变化，实现了磁场能量和电场能量的转换。

4 光敏神经元电路

光线进入眼睛在视网膜上感光并触发神经电活动响应，从物理过程来看，视网膜实现了光电转换，把电磁波能量转化为生物电信号，并以动作电位方式进一步刺激脑视觉功能区来产生响应。光电管和硅光电池被激活后可以作为信号源来驱动神经元电路，一定程度上可以再现视觉神经元电活动响应和模态选择的特征。如图3，在RLC电路中嵌入光电管，利用红限频率以上的电磁波或辐射来激活光电管，光电流在一定范围内变化，会激发这种光敏神经元电路来产生丰富的放电行为。

与图1的RLC神经元电路相比较，光电管相当于信号源，该支路与光电管串联的电阻Rs取值决定了光电管受激发后的性质。当电阻Rs选取比较大的值时，处于工作状态的光电管相当于一个电压源，而电阻Rs选取非常小的值时，光电管激活后相当于给电路施加了一个电流源。根据图3，其对应的电路方程[42]如下:

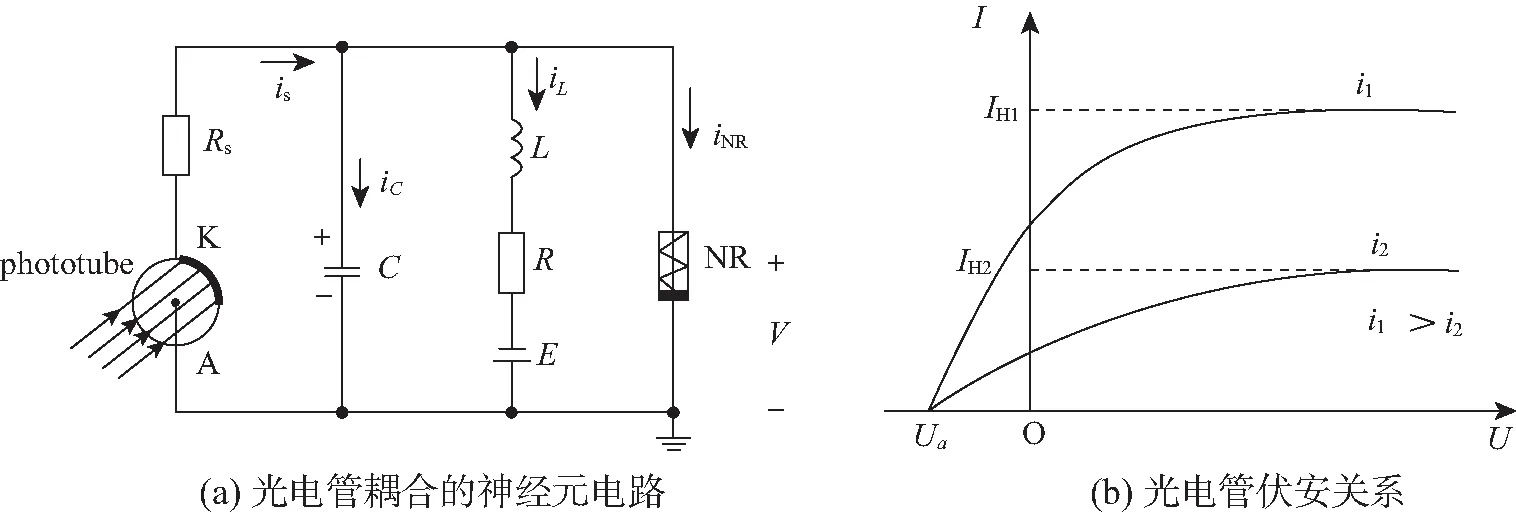
图3 光电管耦合的神经元电路及光电管伏安关系Fig.3 Schematic diagram for light-sensitive neural circuit coupled by a phototube and i-v curve for the phototube

(16)

当光电管看作电压源时，其支路电流为

(17)

当光电管看作电流源时，其通道和支路电流为

(18)

式中：Ua为光电管的反向截止电压或者最大输出电压;IH为光电管的最大饱和电流。对光电神经元电路方程(16)进行如下标度变换，

可以得到广义的光电神经元模型如式(19)。

(19)

实际的光照信号和电磁波都是复合信号，经光电管转化后其光电流和输出电压不再是单一的周期信号，因此us不能选取简单的周期信号，而可以选取多种频率组合的复合信号。从实际意义看，光电管激发的光电流应该存在饱和值，因此，式(18)的光电流is无量纲化后可以等效表达为

is=I0arctan(x-ua)。

(20)

式中：阈值参数ua与光电管反向截止电压(阴极材料属性)有关；I0为光电流的幅度。从实验角度看，如果控制外界光照的强度，也可以有效改变光电流强度的大小，如周期性地调节光照和辐射强度，那么光电流也可以在一定范围内呈现周期性变化，光电管捕获的能量被传递到神经元电路的电容器和感应线圈，以场能量的方式存储和释放，进而触发各类放电模态。从模拟视觉系统角度来看，动物一般都有一双眼睛，从不同光路捕获光学信号来引起视觉系统的知觉，因此，可以研究2个光敏神经元的相位锁定和同步问题来探索视觉神经元之间的协作。

5 压电神经元电路

对于压电器件来说，外界的机械压力和声波引起压电材料和器件的持续形变，就会在压电器件两侧输出电压差，本质上是一种能量转化和能量收集过程。对于听觉神经元来说，外界声波信号经过耳道传递到耳纤毛和螺旋器，这些振动信号引起的力学形变会转化成电信号进一步驱动内神经系统，实现对声音信号的识别。对于普通的压电陶瓷(piezoelectric ceramics)和器件来说，外界机械压力F产生的形变效应可以用压电陶瓷两端输出的电压[43]来表达，

(21)

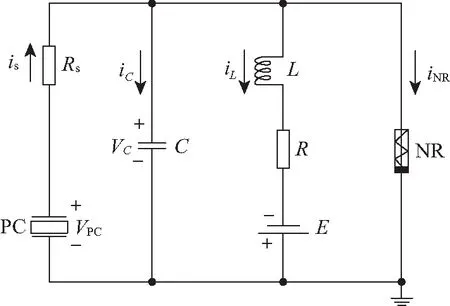
图4 压电神经元电路示意Fig.4 Schematic diagram for piezoelectric neural circuit

式中：Q、S、h和ε分别表示释放的电荷、压电器件的横截面积、厚度和电介质常数；参数d和压电材料的属性有关。压电陶瓷驱动的神经元电路见图4，图中PC表示压电陶瓷。

当压电陶瓷被声波驱动时，其输出的电压信号可以激励神经元电路，对应的电路方程[43]为：

(22)

式中：VPC表示压电陶瓷输出的电压；VC表示电容器输出端电压。采用如下类似标度变换：

(23)

等效的压电神经元方程表示为：

(24)

实际的声波信号并非单一的周期信号，甚至伴随着噪声，因此，压电信号ξuPC可以选取复合信号，如几种不同频率的周期信号的组合，同时也可以考虑加性噪声的影响。在特定环境和条件下，也可以考虑ξuPC为周期信号并伴随噪声信号的情形，研究噪声环境下共振对弱周期信号的识别效果。

6 磁场感知神经元电路

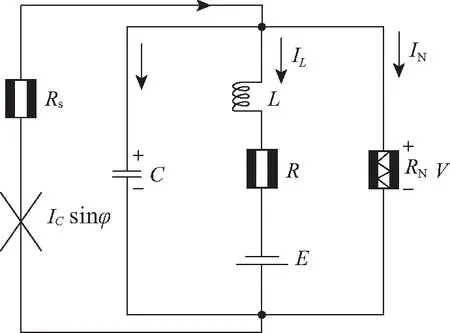
图5 约瑟夫森结耦合的神经元电路Fig.5 Schematic diagram for neural circuit coupled by Josephson junction

约瑟夫森结具有三明治夹层结构，即2个超导端中间置于绝缘层，库伯电子对穿越绝缘层引发的量子隧穿效应使得其通道电流依赖于约瑟夫森结两侧的相位差。从物理角度看，约瑟夫森结具有感应线圈的特征。当约瑟夫森结置于外磁场中时，外磁场会影响库伯电子对对流引起的相位差，在通道电流里产生附加相位差。因此，把约瑟夫森结嵌入到RLC电路中可以感知外界磁场的变化[44-45]，如图5所示。图中ICsinφ表示通过约瑟夫森结的电流，φ表示约瑟夫森结两侧的相位差。

根据基尔霍夫定律和约瑟夫森结的物理属性，对应的神经元电路方程为

(25)

式中：ћ=h/2π表示普朗克常数；e表示电子的电荷量。进一步对神经元电路方程(25)的物理变量和参数进行如下标度变换：

(26)

则对应的神经元模型表达为：

(27)

在变化的外磁场中，约瑟夫森结中的库伯电子对在输运和扩散过程中会受到外磁场(矢势A)的影响，产生一个附加相位，进而影响其通道电流IJJ。

(28)

受外界磁场涨落变化的影响，约瑟夫森结耦合的感知外界磁场效应的神经元模型可以表达为：

(29)

式中Sext表示外磁场变化诱发的相位差变化量，可以选取为周期性或者随机性的序列来对应外界磁场的变化影响。另外，约瑟夫森结也可以用于耦合2个神经元电路，因为耦合通道的可控性，可以实现2个神经元的相位同步，即外磁场对约瑟夫森结[46]的调控可以改变耦合通道的能量输运，进而实现对耦合电路的同步控制。

7 忆阻神经元电路

电磁学理论中4个基本物理量(电压、电荷、电流、磁通量)之间相互关联揭示了电磁场的基本性质，也为设计基本电子器件提供了理论依据。在电压驱动下电荷可以定向运动，运动的电荷产生电流，电流诱发磁场，磁场变化引起回路磁通改变而激发感应电动势，如此循环。欧姆定律揭示了电压和电流的响应关系，电容器充放电解释了电荷存储和电场、电压变化的依赖关系，感应线圈中磁通变化揭示了电流变化和感应电动势的关系。实际上，1972年蔡少棠从磁通量和电荷的关系预言了忆阻器的存在，直到近几年才从技术上实现了忆阻器的制备。从其工作机理来看，忆阻器分为荷控忆阻器φ(q)和磁控忆阻器q(φ)2种。当忆阻器嵌入到电路中，其阻值大小依赖于其通道电流的取值，在给定参数结构下，非线性电路的动力学也会受到记忆变量初始值的影响。在设计磁场可控的记忆电路时，通常在非线性电路中并联磁控忆阻器，而设计电场可控的记忆电路时，则在非线性电路中并联荷控忆阻器。一个关键问题是，无论磁控忆阻器还是荷控忆阻器，对其电路方程进一步进行非线性分析时必须对磁通变量和电荷量进行标度变换，以得到无量纲的动力学方程。当RLC电路中分别并入磁控忆阻器和荷控忆阻器，其广义的电路方程表示为：

当然，忆导函数ρ(φ)和忆阻函数M(q)可以选取其他类型的表达式。对于电压变量、电流变量和时间变量的标度变换遵循前几种情况类似的规则，磁通和电荷变量的标度[47]变换可以采用如下规则：

(30)

磁控忆阻器与荷控忆阻器耦合的非线性电路对应的无量纲动力学方程等效表达为：

(31a)

(31b)

从动力学角度看，忆阻系统(30)、(31)的参数固定时，改变记忆变量w或者z的初始值也会引起动力学轨道的切换，且吸引子的类型也会发生改变，即初始值的敏感性大幅度增强。2个忆阻系统在达到耦合同步后，改变其中一个系统的初始值，系统的同步稳定性会受到破坏[48]，因为初始值的改变已经彻底改变了忆阻系统的动力学，如吸引域和吸引子稳定性。这些包含忆阻器的电路系统对应的电路方程无量纲化后可得到忆阻振子，当更多的忆阻振子和系统耦合起来构建忆阻网络，其网络群体动力学的同步稳定性和时空斑图形成[49]也会受到初始值的影响。一般地，忆阻振子的动力学方程为：

(32)

式中：z表示记忆变量，如电路方程里的磁通变量；Iext表示外部刺激；-kz2x表示记忆函数；Srandom表示随机序列，当反馈增益k′不等于零时，记忆变量会受到连续的扰动而诱发轨道的切换，使得系统的动力学更加依赖于初始值的选取。对于生物神经元来说，离子在细胞内外输运过程中必然诱发时变的电磁场，这必然对离子跨膜输运和神经元膜电位产生影响，特别地，神经系统每个功能区都聚集了大量神经元，这种电磁场效应的作用显然是不能忽略的。2016年，本团队基于量纲一致原理，考虑忆阻器的物理属性和生物神经元的突触功能，提出在Hindmarsh-Rose神经元模型里引入磁通变量，用感应电流来表达这种电磁感应效应[50]，并把该方法用于其他生物神经元模型及心肌组织中，能够很好地解释电磁辐射对神经元及心肌组织的影响。

(33)

在构建忆阻神经元模型中，本团队采用磁控忆阻器的形式。其中，Iext对应这等效的外界刺激，而-kρ(φ)x表示感应电流，这与介质的属性有关，φ、x、y、z分别表示无量纲化后的磁通量、膜电位、恢复变量对应的慢电流、自适应电流变量。忆导函数ρ(φ)中的参数(α,β)取决于介质如忆阻性突触的属性。因为介质中的磁场效应，参数k1=1/N,即除了考虑神经元膜的电容效应，神经元被当做一个N匝线圈来表达磁场效应。当神经系统暴露于电磁辐射下，实际上改变了每个神经元对应的磁通量，因此可以在第四变量的动力方程右侧施加周期性或噪声序列φext来表达外界电磁辐射引起的效应。电突触和化学突触可用不同方式连接神经元并调节神经元的同步行为，考虑了神经元细胞膜内外离子输运产生的电磁感应后，这意味着神经元之间也存在场耦合效应，这对神经元突触的功能有一定的调控。对于忆阻神经元，在神经元网络中，场耦合过程本质上是磁通量交换，进而导致神经元网络内不同位置处的神经元对磁通量贡献不同的权重，各个神经元内部的感应电流也不同。在一维空间上，以忆阻性的HR神经元模型式(33)构建链状网络[51]，其动力学方程为：

(34)

这里只考虑了网络各向同性的情形，周围的神经元都以相同的权重来影响每个神经元的磁通，变量下标i表示网络内神经元的位置或次序。类似地，该方法可以推广到二维空间规则网络、小世界网络以及多层网络，考虑边界条件、噪声、外界刺激电流及感应强度k对神经元网络群体电活动的影响。基于平均场理论，可以分别定义一维和二维神经元网络的同步因子R如下：

(35a)

(35b)

对于一维神经元网络，N表示总的神经元个数，对于二维神经元网络，N2表示神经元总数量。〈*〉表示对变量求时间平均，当R取值接近于1时表示系统达到完美同步，神经元网络趋于均匀态，而当R非常小则表示系统处于非同步状态，此时在网络中可能诱发出对称性的时空斑图。神经元网络可以研究离散介质的行波和斑图稳定性，而对于连续介质来说反应扩散系统方程能更好地表达其行波传播和群体动力学。本团队改进了二变量的心肌模型，分别研究了电磁辐射对正常心脏和心律不齐状态下心肌组织电活动的响应问题，包含电磁感应的心肌电活动模型[52-53]在电磁辐射下动力学方程为

(36)

式中：变量u、v表示心肌组织中膜电位；Ist表示外界等效的跨膜刺激电流；-ku(u-a)(u-1.0)-uv表示总的细胞膜离子通道电流；k0ρ(φ)x表示感应电流；φext表示外界电磁辐射(高频、低频或者噪声)；Du是扩散系数。参数值选取为a=0.15,μ1=0.2,μ2=0.3,k=8.0,ε=0.002,k0=1,k1=0.2,k2=1.0,α=0.1,β=0.2，当感应电流强度k0=0时就退化为没有电磁感应效应的情形。正常健康的心脏中窦房结连续射出的电信号在心肌组织里传播形成靶波，对心肌细胞内钙离子浓度产生影响。钙离子浓度的增加导致肌肉收缩，因此，心肌中的靶波通过调控钙离子流来控制肌肉收缩而对心肌泵血过程进行调控。本团队研究结果表明，不断增加电磁辐射的强度到一定阈值，心肌中的靶波传播被限制在很小的区域内，这意味着窦房结射出的信号无法控制整个心肌组织中钙离子浓度和钙流，因此，心脏的收缩受到抑制导致泵血不足而休克。另一方面，在心律不齐时，心肌组织中钙离子被螺旋波控制，逐渐增大电磁辐射强度，螺旋波会发生破裂，心肌进入心颤状态导致猝死。

8 神经元的滤波和选频特性

视觉神经元对特定频段光照和电磁辐射非常敏感，如正常人对可见光感知的波长范围在400～760 nm之间，而人类听觉系统对声波敏感的范围在20～20 000 Hz，超出这个频段和波长范围的信号则被过滤掉，因而无法被神经系统感知。如前所述，利用光电管的感知功能可以设计感光神经元电路来研究视觉信号感知，利用压电器件可以设计压电神经元电路来研究听觉信号感知。在光电管和压电陶瓷表面分别镀膜，对外界的光信号和声波信号可以实现过滤和筛选。考虑到实际的光信号和声波并非单一的周期信号，因此可以采用实际的复合信号或者混沌电路输出的序列来模拟实际信号，2021年本团队提出一种滤波标准来分析视觉神经元和听觉神经元的选频机制[54-55]，即实际的信号包含多种频率和波段，超过设定阈值的信号则被快速衰减或过滤，

(37)

(38)

式中参数λ取值越小，表明滤波和选频效率越高。从控制角度看，这是一种限频控制，可以利用阶跃函数来设计恰当的上下阈值，对实际信号滤波过程为

s′(τ)=A(ω)cosωτ=[H(ω-ωmax)+H(ωmin-ω)]A0exp(-τ/λ)cosωτ+

A0[H(ωmax-ω)+H(ω-ωmin)-1]cosωτ。

(39)

实际的信号滤波后仍然包含一定波段，对光敏神经元和听觉神经元电活动模态能产生有效的控制。

9 耦合通道和突触可塑性

神经元的突触在接收和传递信息中非常关键，电突触耦合是一种间隙耦合，响应过程非常快，其物理过程是基于间隙电阻实现的电位耦合。化学突触耦合依赖于突触端神经递质的释放，进而影响钙离子流，因而其作用过程比较慢，从物理角度看是一种场耦合。对于非线性电路与神经元电路来说，很多电子器件如线性电阻、热敏电阻、忆阻器、电容器、感应线圈、约瑟夫森结、光电管都可以用来连接电路的输出端，以实现不同类型的耦合并分析其同步稳定性。从控制角度来看，耦合通道的可控性意味着耦合强度可以在很大范围内调制，在实验上也具有可操作性。当电阻嵌入到耦合通道中，在耦合过程中必然伴随着焦耳热的消耗，而且有累加效应，这对于大规模阵列的神经元电路的稳定性显然是有负面影响的。基于电阻连接的电压耦合，实际上是通过消耗非线性电路的能量来实现能量平衡，进而达到同步控制的目的。当电容器和感应线圈嵌入到耦合通道中，耦合电路的部分能量被抽运和暂存于耦合通道中，在耦合通道中改变电介质和磁介质的容量或密度则可以实现对耦合通道的操控，进而控制能量平衡过程，最终实现非线性电路的同步。从动力学角度来看基于电容器的耦合是一种微分耦合，而基于感应线圈的耦合则是一种积分耦合，其耦合通道的电流分别表示为

(40)

式中：C、L表示耦合通道电容器和感应线圈对应的电容值与电感值；iC、iL分别表示耦合通道中电容器和感应线圈的电流；V、V′ 表示电路输出端的电压。在实际控制中，可以采用单一的电子元件来建立耦合通道，也可以利用多个电子元件组合来建立耦合通道。对于神经元电路来说，把电阻、电容器、感应线圈和忆阻器组合起来可以设计混合突触，用于研究神经元电路及网络同步稳定性。从实际情况来看，生物神经元的树突非常稠密，可以实现多通道信号输入，神经元细胞本身也具有一定柔性，因此神经元突触缠绕在一起时其耦合过程可能非常复杂，见图6[56]。

图6 神经元之间的混合突触连接与耦合[56]Fig.6 Schematic diagram for neurons coupled by hybrid synapses[56]

化学突触的耦合过程中，突触结构在神经元电路中等效表达为电阻、电容器与感应线圈的组合，以实现电压耦合和场耦合，见图7。

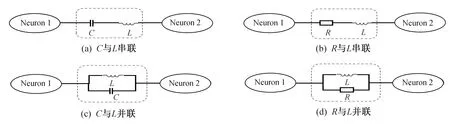
图7 神经元电路耦合时混合突触的实现Fig.7 Realization of hybrid synapses connected to neurons

突触可塑性(synaptic plasticity)表达了神经元突触连接的长时间改变的能力，或者动态适应性。在神经科学中，突触可塑性是突触随着时间的推移而增强或削弱的能力，以响应其活性的增加或减少，兴奋性突触和抑制性突触的可塑性都取决于突触后钙的释放。突触可塑性主要包括短期突触可塑性(short-term synaptic plasticity，SSP)与长期突触可塑性(long-term synaptic plasticity，LTSP)。短期突触可塑性主要包括易化(facilitation)、抑制(depression)、增强(potentiation)。长期突触可塑性主要表现形式为：长时程增强(long-term potentiation，LTP)和长时程抑制(long-term depression，LTD)。2个神经元之间突触连接(长期增强或LTP)有效性的长期变化可能涉及突触触点的形成和断裂。如果突触的强度仅通过刺激增强或由于缺乏突触而减弱，则将产生正反馈回路，导致一些细胞从不放电，一些细胞频繁放电。但2种可塑性调节形式(缩放性和可塑性)也存在，以提供负面反馈。突触缩放是神经元能够稳定上下发射率的主要机制。突触缩放有助于保持突触相对于彼此的强度，降低小兴奋性突触后电位的振幅，以应对持续的兴奋，并在长时间阻塞或抑制后提高它们。突触缩放是神经元选择性地选择其不同输入的主要机制。长期增强作用(LTP)又称长时程增强作用、长期增益效应，是由于同步刺激2个神经元而发生在2个神经元信号传输中的一种持久的增强现象。长期抑制作用(long-term depression，LTD)又称长时程抑制作用、长期抑势，指神经突触持续几个小时到几天的抑制行为。强烈的突触刺激(小脑Purkinje细胞)或者长期的弱突触刺激(海马体)均可导致长期抑势的形成,现已发现突触传递的可塑性除了与学习记忆功能关系密切外,还参与了感觉、心血管调节等其他重要生理或病理过程, 突触可塑性对神经元模态的调控影响见文献[56]。从物理角度看，突触可塑性对应耦合通道中人工突触可控性和自适应性，对应场能量输运和存储的过程。从控制角度看，耦合通道的激活和可控性对应于突触连接和突触电流自适应性，如2个或者多个神经元之间能量不平衡时，突触被唤醒并不断增强直到神经元之间达到能量平衡，神经元在不同放电模态下达到相位锁定或者完全同步。

10 神经元网络

神经系统由大量的神经元构成，20%的神经元是抑制性的，而80%的神经元是兴奋性的。兴奋性神经元和抑制性神经元共同作用对维护神经系统的安全性非常关键，在理论模型上主要以突触电流函数不同形式来区分。突触可以分为兴奋性突触(excitatory synapses)和抑制性突触(inhibitory synapses)。前者主要传递兴奋性神经递质，如谷氨酸(glutamate)、肾上腺素(epinephrine)、去甲肾上腺素(nor-epinephrine)、多巴胺(dopamine)、血清素(5-HT)、乙酰胆碱(acetylcholine)和组胺(histamine)；而后者主要传递抑制性递质，如γ-氨基丁酸(GABA)和血清素(5-HT)。兴奋性神经递质的传递导致接受神经元的钠离子通道打开，钠离子流入使得该神经元内部正电荷升高，细胞去极化(depolarization)；而抑制性神经递质的传递导致接收神经元的钾离子和氯离子通道打开，钾离子流出而氯离子流入，使得该神经元内部负电荷升高，细胞超极化(hyperpolarization)。在理论神经科学中，会明确地划分兴奋与抑制性神经元。抑制性神经元产生了抑制性突触电流，一般在仿真的时候把它当作负值, 而兴奋性突触电流则是正值。使突触后神经元放电率提高的突触前神经元就是兴奋性神经元，反之使突触后神经元放电率降低的突触前神经元就是抑制性神经元。抑制性神经元产生抑制性离子，如γ-氨基丁酸(GABA)，抑制性递质进入兴奋性神经元，降低正负电离子的浓度比，防止细胞过热而死亡，这对神经元和细胞起保护作用。

神经系统电活动的触发和模态的选择取决于大量神经元的协作，这种协作的有效性取决于神经元网络或神经介质局域激发性，耦合通道属性、扩散属性和连接拓扑结构。在利用复杂网络表达神经元群体电活动特征时，通常要考虑神经元功能属性及网络边界条件影响。对于脑皮层同一功能区，可以选择同种性质的神经元来构建单层网络或者单条链状网络，也可以考虑激发性神经元和抑制性神经元共存的情形。若考虑到神经系统功能区的差异性，在研究不同功能区的协作效应时，则可以设计多条链状网络或者多层网络来研究其时空斑图和同步稳定性。如式(35)所定义，通常要计算关联统计量来分析时空系统的稳定性和斑图控制，其中要考虑到电磁辐射、噪声、异质性和非均匀性、边界条件和初始值的约束效应。对于神经元网络而言，时空斑图的形成源于系统的自组织性，经稳定性分析可以发现时空系统历经霍普分岔产生螺旋波，而历经鞍结分岔可以诱发图灵斑图。从网络拓扑结构来看，无论规则网络、小世界网络，还是无标度网络都是链路优化的结构，旨在提高信息编码和传输的效率。复杂网络方法可以研究广义神经元群体电活动的动力学特征和模态选择规律，但对于实际的生物系统则应该考虑其功能性差异、生物物理效应、及自适应性控制的内在机理。

可靠的神经元模型对认知神经系统内复杂的电生理活动、神经元之间的协作和自组织行为非常关键。此前关于神经动力学的研究主要集中于广义神经元模型，通过分岔和随机共振分析能一定程度了解神经元电活动模态选择的动力学机制，对2个或者更多的神经元则可以从网络同步和时空斑图方面展开研究，从单个神经元到胶质细胞耦合的神经元网络，多层神经元网络可以研究神经系统群体电活动的控制，为预防神经性疾病提供一定参考。基于本团队提出的系列功能性神经元模型，可以把不同功能的神经元连接来构造小网络来分析脑皮层不同功能区神经元协作问题[57]，也可以把不同功能神经元用来构造多层网络，研究多层网络的协作和同步控制问题[58-62]。胶质细胞对神经系统中神经元电活动也有重要调制作用，相关进展可参看文献[63]及其中的文献。

11 结语

从物理学角度系统介绍了多种功能神经元电路设计、能量计算和操控、混合突触设计和可控性、电磁辐射和场耦合效应等，解释电磁辐射引发心脏死亡和休克机制，神经系统的滤波机制。系列研究工作强调物理学基本原理和非线性科学结合的重要性，指出同步过程中耦合通道可塑性及其能量平衡的重要性，这些结果为进一步研究计算神经科学、智能传感器设计和控制提供了思路。