双闭环滑模控制移动机器人的运动轨迹

冯巧红

(滁州职业技术学院 电气工程学院，安徽 滁州 239000)

移动机器人作为当今的智能化产品之一，给人们的日常生活带来了极大的便利。但目前移动机器人控制系统普遍存在响应速度相对滞后、控制精度不高的问题，只能执行相对简单的重复性工作，无法完成复杂任务，尤其是在未知环境中工作时[1-2]。如何让移动机器人更好地为人类服务，控制系统的设计至关重要。Nabanita等[3]和席万强等[4]研究了机器人自适应滑模控制方法，引用了自适应滑模控制器，较好地提高了机器人运动路径的跟踪精度。尤波等[5]和Yin等[6]研究了移动机器人模糊滑模控制方法，建立了其位置坐标，定义了运动轨迹误差方程式，设计了模糊滑模控制器，降低了移动机器人运动位置误差。滕昊等[7]和赵安等[8]研究了机器人双环滑模控制方法，建立了机器人运动学模型，提出了机器人双环路径跟踪控制系统，使响应速度和控制精度都得到了改善。以上研究都是针对控制系统功能的实现，而控制精度仍是研究的难点。

本文以移动机器人简图为例，推导机器人运动学方程式，采用内环和外环双重工作模式，设计双闭环滑模控制系统，以提高运动位置和旋转角度的跟踪精度，最后采用MATLAB进行仿真检验，对比不同控制方法的轨迹跟踪误差大小，为后期深入研究移动机器人控制理论提供参考。

1 移动机器人模型

移动机器人模型如图1所示。移动机器人模型有3个轮子，左右两侧各有1个驱动轮，前部有1个被动轮，操纵器有3个连杆。移动机器人的变量定义如下：τl，τr，τ1，τ2，τ3分别为左轮、右轮、接头1，2，3上的扭矩；θl，θr分别为左、右轮的旋转角度；R和φ为移动平台向前移动位置和旋转角度；θ1，θ2，θ3为连杆1，2和3相对于z0，z1和z2轴的旋转角度；mp，mw，m1，m2，m3为移动平台、车轮、连杆1，2和3的质量；Iz和Iw为移动平台和车轮相对于z0轴的惯性矩；d为质心C与左、右两车轮之间的距离；r为车轮的半径；l1，l2，l3为连杆1，2，3的长度。

图1 移动机器人模型

移动平台质心C的位置表示为x和y，则左、右2个车轮的质心位置为：

(1)

设r1，r2和r3表示关节和连杆质心之间的距离,则连杆1，2和3的质心坐标为：

(2)

受非完整约束的系统动力学[9]公式为：

(3)

轮胎动力学方程式定义为：

(4)

(5)

2 控制器设计

2.1 移动平台的运动学方程

三轮移动平台系统具有3个自由度qv=[xyφ]T，三轮移动平台的速度关系为：

(6)

式(6)中，vl为移动平台的线速度；ω为移动平台的角速度；Jv(φ)为变换矩阵。

非完整速度约束驱动轮完全滚动且不打滑，只能沿垂直于驱动轮轴的方向移动，则：

y′cosφ-x′sinφ=0

(7)

(8)

式(8)中，AT(qv)=[-sinφcosφ0]T。

2.2 外环控制设计

实际姿态和期望姿态之间的跟踪误差定义为：

(9)

移动平台外环的滑动面[10]定义为：

(10)

式(10)中，kvoe为1个增益矩阵。

将虚拟速度指令vvc作为移动平台速度vv的虚拟控制，可以得到：

(11)

为了满足稳定性条件，定义：

(12)

式(12)中，kvo1，kvo2，kvo3为增益矩阵；εvo，γvo为常数。

2.3 内环控制设计

采用双闭环控制的移动机器人控制流程如图2所示。

图2 采用双闭环控制的移动机器人控制流程

辅助跟踪误差和指令误差定义为：

evi=vv-vvc

(13)

(14)

式(14)中，λvi为常数矩阵。

选择过滤后的二阶误差面为：

svi=vv-rvi

(15)

为了满足稳定性条件，选择动态控制率为：

(16)

式(16)中，kvi1，kvi2，kvi3为常数矩阵；εvi，γvi为常数。

3 误差仿真

通过MATLAB软件对移动机器人运动位移和角度跟踪误差进行仿真，分析移动机器人控制系统的稳定性，参数设置为：mp=6 kg，mw=0.7 kg，m1=m2=m3=0.6 kg，l1=l2=l3=0.2 m，d=0.15 m，r=0.08 m。

假设移动机器人运动轨迹为x2+y2=1，移动机器人在X和Y方向的位移跟踪误差分别如图3和图4所示。

图3 X方向的位移跟踪误差

图4 Y方向的位移跟踪误差

由图3可知，在X方向，采用滑模控制器的移动机器人跟踪精度较低，误差范围为[-2.0×10-2,2.0×10-2]m，采用双闭环滑模控制器的移动机器人跟踪精度较高，误差范围为[-0.5×10-2,0.5×10-2]m，跟踪误差范围降低了1.5×10-2m。由图4可知，在Y方向，采用滑模控制器的移动机器人跟踪精度较低，误差范围为[-2.5×10-2,2.5×10-2]m，采用双闭环滑模控制器的移动机器人跟踪精度较高，误差范围为[-0.7×10-2,0.7×10-2]m，跟踪误差范围降低了1.8×10-2m。

移动机器人在旋转方向的角度跟踪误差如图5所示。由图5可知，在旋转方向，采用滑模控制器的移动机器人跟踪精度较低，误差范围为[-1.0,1.0]deg，采用双闭环滑模控制器的移动机器人跟踪精度较高，误差范围为[-0.5,0.5] deg，跟踪误差范围降低了0.5 deg。因此，在相同工况条件下，采用双闭环滑模控制器的移动机器人运动轨迹跟踪反应速度较快，跟踪精度较高，能够利用反馈信号进行自适应调整，具有较强的鲁棒性。

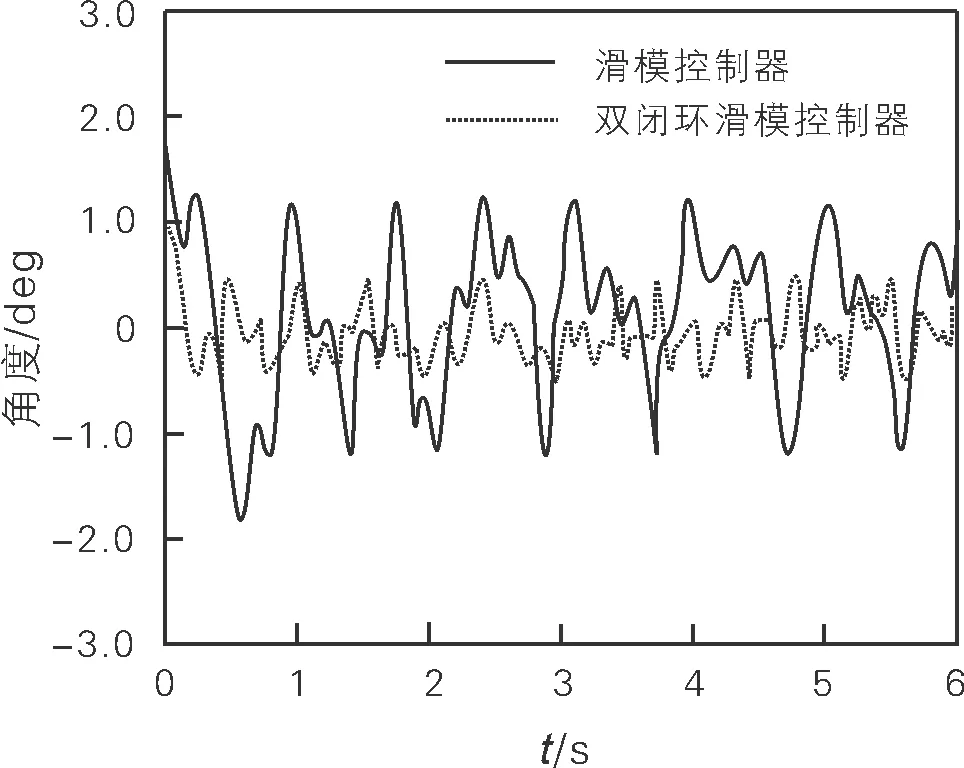
图5 旋转方向的角度跟踪误差

4 结论

针对移动机器人追踪目标误差较大的问题，设计了双闭环滑模控制系统，利用仿真软件分析了移动机器人运动位移和角度追踪误差，主要结论如下。

1)采用滑模控制器的移动机器人在X和Y方向的运动位移以及在旋转方向的角度跟踪误差变化范围分别为[-2.0×10-2,2.0×10-2]m，[-2.5×10-2,2.5×10-2]m和[-1.0,1.0]deg，输出误差范围较大，只适合低精度或者精度要求不高的控制系统。

2)采用双闭环滑模控制器的移动机器人在X和Y方向的运动位移以及在旋转方向的角度跟踪误差变化范围分别为[-0.5×10-2,0.5×10-2]m，[-0.7×10-2,0.7× 10-2]m和[-0.5,0.5]deg，误差变化范围较小，适合高精度的控制系统。