基于在线泛化神经网络算法的混合试验方法

孟丽岩， 周天楠， 王 涛

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

0 引 言

基于模型参数识别方法的参数识别效果依赖于事先假定模型精度，当结构及构件进入强非线性状态或者无法预知复杂对象数值模型时，将限制该参数识别方法的实际工程应用。神经网络算法因其对结构及构件进入强非线性部分具有较好的拟合效果，以及无需预先知晓模型等优点而受到研究者们的广泛关注，成为混合试验中模型更新的新途径。

Yang[1]通过从试验子结构获得的位移和恢复力作为训练集，离线训练BP神经网络，将训练好的网络作为数值子结构模型，得出在线预测其恢复力的精度较高。Yun等[2-3]获得了五变量输入的神经网络模拟梁柱节点滞回性能。Elanwar等[4]将神经网络算法应用到两跨钢框架结构混合试验，证明了采用神经网络算法进行材料本构混合试验的有效性。Konstantinos等[5]采用离线多层感知器网络对钢筋混凝土结构的损伤状态进行优化预测，指出至少有5个地震参数作为输入时，人工神经网络可以很好地预测钢筋混凝土结构的震害状态。周天楠等[6-7]在标准在线神经网络算法的基础上，提出了在线泛化神经网络算法，分别采用不接续和接续训练方式预测RC柱恢复力,指出接续训练方式具有更强的灵活性和抗干扰能力。

笔者将接续训练的在线泛化神经网络算法应用于两自由度结构混合试验中，验证该混合试验方法的可行性，并与基于在线神经网络算法的混合试验方法[8](Hybrid test method based on online neural network，HTNN)的预测能力进行对比分析。

1 在线泛化神经网络算法

在线泛化神经网络算法有两种：第一种为在所获得的所有组数据中，测试集为选取的一组数据，训练集为其他的所有组数据，采用Elman神经网络算法在线训练选取的训练集，对测试集进行预测，该方法为不接续训练的方法；第二种为每次仅在线训练一组数据，在当前组数据训练完成后保留tr变量，并将这一变量传递到下一组训练中，使得在接下来的训练中，下一组数据可以在当前组数据训练后进一步在线训练网络，以此类推，直至所有的训练集输入完毕，最后对测试集进行预测，称为接续训练的方法。采用这种接续的训练方式既可以使通过训练神经网络算法获得的权值和阈值具有承袭性，又可以在训练时不用事先要求训练集中数据为确定的组数，算法具有灵活性，接续训练方式下的在线泛化神经网络算法的流程如图1所示。

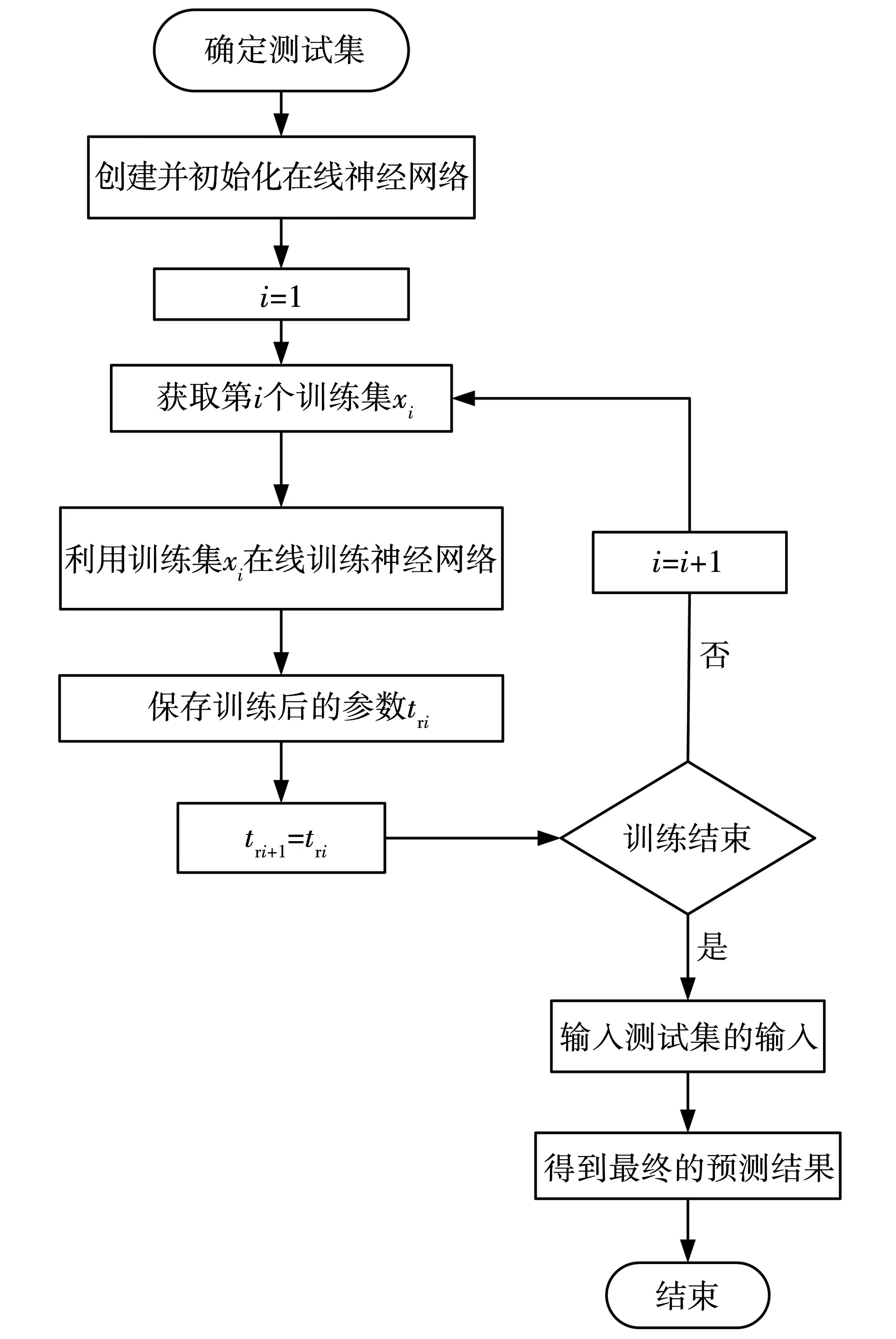
图1 接续训练方式下的在线泛化神经网络算法流程Fig. 1 Online generalized neural network algorithm flow under continuous training mode

2 混合试验方法原理

为了解决不同结构参数下数值子结构和试验子结构恢复力预测的问题，文中将泛化神经网络算法应用于结构混合试验中，即在线泛化神经网络混合试验方法(Hybrid test method based on online generalized neural network，HTGNN)。该方法的主要思想：首先，通过Bouc-Wen模型模拟试验子结构，获得多组混合试验不同结构参数下试验子结构的位移和恢复力，以此作为在线泛化神经网络算法的输入样本；其次，利用这些输入样本采用接续训练方式训练网络，获得具有混合试验子结构一定经验信息的神经网络模型；最后，将神经网络模型应用于混合试验，进行在线训练及在线预测数值子结构恢复力。HTGNN采用神经网络算法进行试验子结构在线训练时，利用已训练好的且具有一定试验子结构信息的神经网络模型，而不是采用重新定义的与之前训练毫无关联的全新的神经网络模型。HTGNN原理如图2所示。

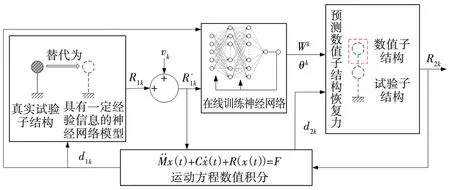
图2 HTGNN原理Fig. 2 Principle of HTGNN

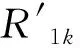
3 混合试验方法数值验证

3.1 研究对象及其参数

为检验HTGNN的有效性，以一个两自由度的集中质量剪切模型作为研究对象进行数值仿真，第一层为试验子结构，第二层为数值子结构。两层结构恢复力模型均采用Bouc-Wen模型[9]，恢复力为

(1)

式中：k——结构的初始刚度；

x——结构的位移；

α——第二刚度系数；

z——滞变位移；

A——滞变位移的初始刚度；

β、γ、n1——影响滞回曲线形状的参数；

F——结构恢复力。

两层集中质量剪切模型的参数分别为：结构质量m1=m2=3 750 t，系统结构刚度k1=k2=592 177.5 kN/m，系统结构阻尼为c1=c2=7 539.75 kN/(m·s-1)，α=0.01，A=1，n1=1。通过改变Bouc-Wen模型参数β和γ进行模拟不同结构参数下的钢筋混凝土结构恢复力特性，多组不同试验子结构上获得相应的位移和恢复力，作为接续训练方式下在线泛化神经网络算法的训练集，同时也作为混合试验的输入地震动。网络训练时试验子结构Bouc-Wen模型参数β和γ取值如表1所示。

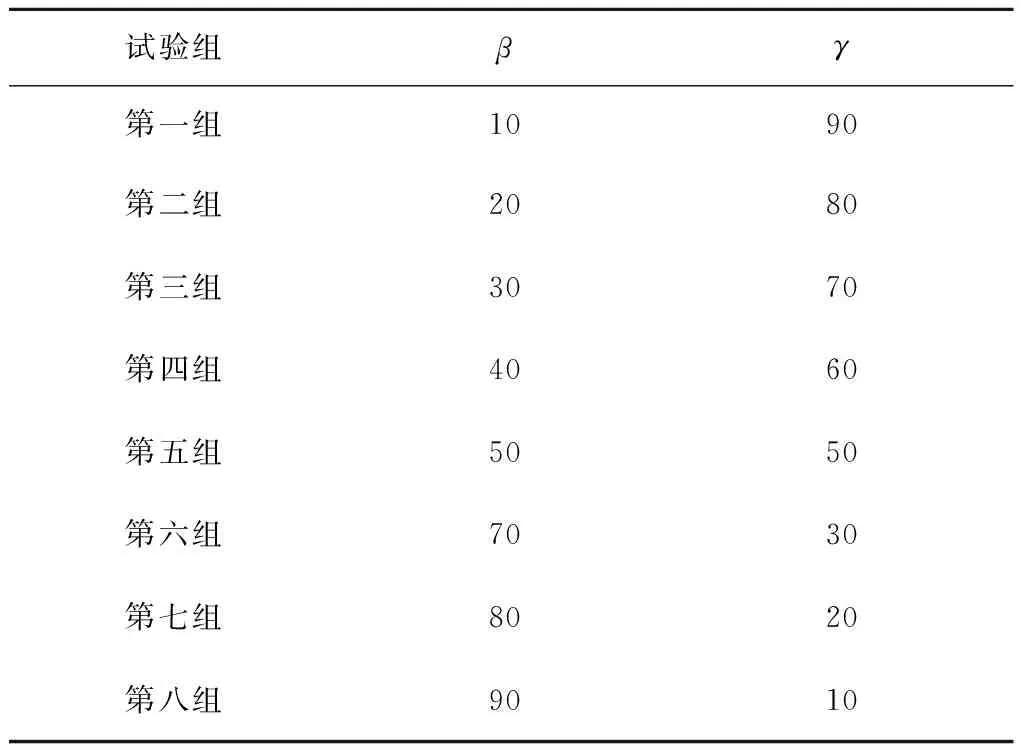
表1 试验子结构Bouc-Wen模型参数

在混合试验时，假定试验子结构模型参数β和γ分别为60和40，数值子结构模型参数β和γ分别为40和60。采用网络接续训练方式进行HTGNN数值仿真，网络拓扑结构包含两个隐含层，每层设置15个神经元，激活函数选择双曲正切函数，输出层中定义输出变量为恢复力，激活函数采用纯线性函数，训练方法选用BFGS拟牛顿BP算法，设定最大训练步数为100步，目标误差设定为10-7。

3.2 试验与结果分析

文中提出方法的模拟步骤如下：首先采用El-Centro波对不同参数下的结构进行加载，获得多组不同结构参数下试验子结构的位移和恢复力，以此作为接续训练方式下在线泛化神经网络算法的训练集；再对神经网络进行在线训练，获得具有一定信息经验的神经网络模型，将El-Centro波作为混合试验的地震动输入，混合试验训练试验子结构时直接采用训练过的神经网络模型，最终预测数值子结构的恢复力。

该混合试验得到的预测结果如图3～5所示。下层位移曲线和上层位移曲线如图3所示。下层恢复力曲线和上层恢复力曲线如图4所示。下层滞回曲线和上层滞回曲线如图5所示。

由图3～5可以看出，HTGNN得到的上下层位移时程曲线、上下层恢复力时程曲线，以及上下层结构滞回曲线均与参考解均具有较好的拟合效果，验证了该混合试验方法的可行性和有效性。

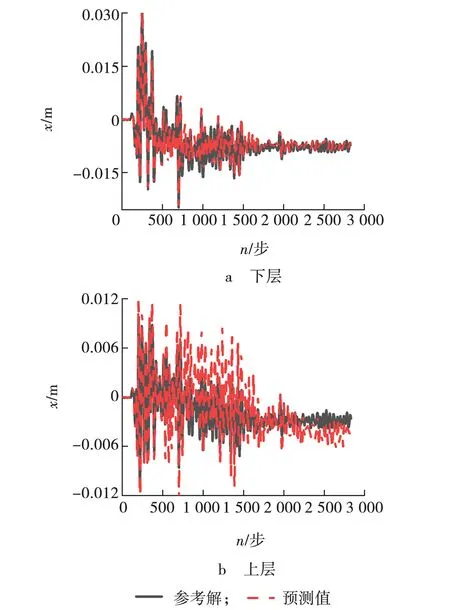
图3 位移时程曲线Fig. 3 Displacement time history curve

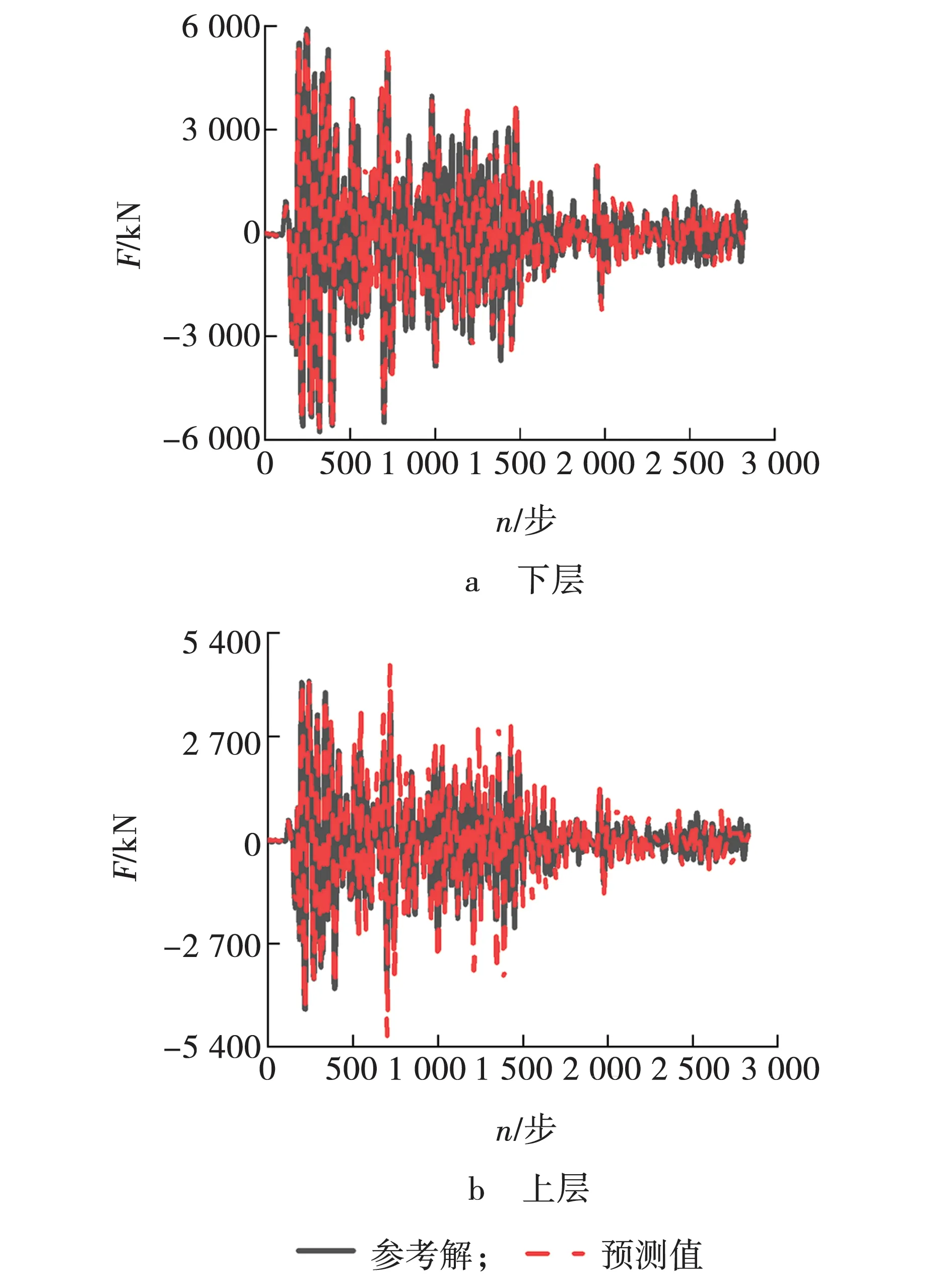
图4 恢复力时程曲线Fig. 4 Time history curve of restoring force

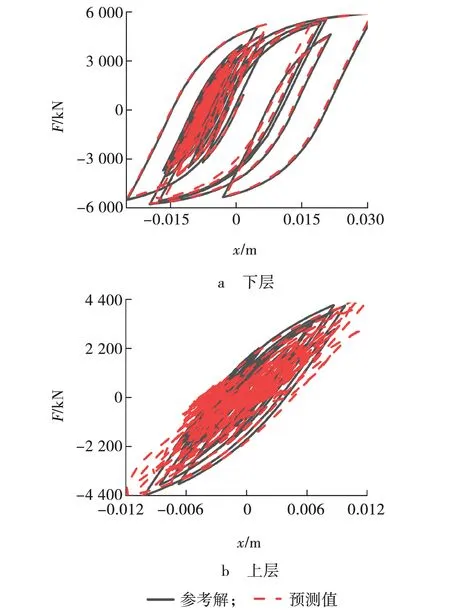
图5 结构滞回曲线Fig. 5 Structural Hysteresis Curve

3.3 恢复力预测对比分析

为进一步验证HTGNN与HTNN[10]在数值子结构恢复力预测能力方面的差异性，采用仅改变神经网络算法对试验子结构的训练方式，预测相同结构参数的数值子结构的恢复力，由Bouc-Wen模型计算所得的数值子结构恢复力预测结果定义为参考解，上层数值子结构滞回曲线对比如图6所示。

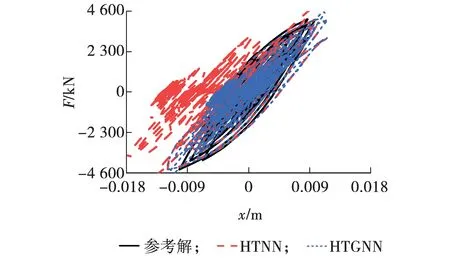
图6 滞回曲线对比Fig. 6 Comparison of hysteresis curves

由图6可知，与HTNN相比，HTGNN得到的滞回曲线与参考解曲线更加接近，HTGNN的均方根误差为0.437 59，HTNN的均方根误差为0.443 56，降低了恢复力预测误差。

为验证HTGNN与HTNN计算效率，分别取五次训练的计算耗时并取平均值进行比较。五次混合试验的计算耗时如表2所示。

表2 计算耗时对比

由表2可知，在计算耗时方面，HTGNN和HTNN5次的平均计算耗时分别为133.25和148.69 s，前者比后者减小了10.4%，HTGNN算法具有更高的计算效率。

HTGNN在预测数值子结构的恢复力精度和计算效率两个方面均优于HTNN。前者具有更好预测性能的主要原因在于，事先对神经网络进行了训练，使算法蕴含一定的试验子结构的信息，能更好地识别混合试验中试验子结构的数据分布，使数值子结构的预测精度提高。由于建立的神经网络包含了先验知识，提高了混合试验中神经网络训练速度，使HTGNN具有更高的计算效率。

4 结 论

(1)提出了一种基于泛化神经网络混合试验方法，通过一个两自由度结构混合试验数值仿真，验证了所提试验方法的有效性。

(2)与基于在线神经网络算法的混合试验相比，泛化神经网络混合试验方法在降低预测结果误差和缩减计算耗时方面均具有明显优势，其中后者的计算效率提高10.4%。由此可见，泛化神经网络混合试验方法可获得更好的预测精度和更高的计算效率。