基于ARIMAX 的开封“7·20”特大暴雨城市内涝预报研究

喻谦花，冯 峰，罗福生，霍继超，冯跃华，张鹏飞

（1.开封市气象防灾减灾重点实验室，河南 开封 475004； 2.黄河水利职业技术学院，河南 开封 475004；3.河南省黄河中下游水资源节约集约利用工程技术中心，河南 开封 475004；4.河南省豫东水利工程管理局，河南 开封 475004）

2021 年7 月20 日，河南省遭遇极端强降雨。 7 月18 日8 时至20 日15 时30 分，郑州荥阳、巩义的7 个雨量站降雨量超600 mm，最大点雨量718.5 mm［1］。极端强降雨引起河南多地出现严重城市内涝，防汛形势十分严峻［2］。 城市内涝威胁城市居民生命财产和出行安全，造成了巨大经济损失［3-4］。 近年来聚焦于城市内涝的研究主要集中在内涝引发的灾害、形成的原因、治理的措施等方面［5-9］。 对于城市内涝模拟和预报研究，栾震宇等［10］基于MIKE FLOOD 平台将MIKE URBAN 和MIKE 21 模型耦合，建立城市内涝模型，对湖南省新化县典型区域的排涝情景进行模拟，表明该模型适用于城市内涝风险评估管理；曾照洋等［11］将SWMM 一维管网模型及LISFLOOD-FP 二维水动力模型进行耦合，对东莞市典型区域进行暴雨内涝模拟，实现了研究区暴雨内涝淹没范围与淹没水深的模拟；陆敏博等［12］以苏州市相城区为例，采用Mike 模型建立排水防涝系统耦合模型，同时考虑平原河网地区城市排水防涝特征，将恒定均匀流推理公式法、水量平衡法与数学模型法相结合，评估多种情景下的雨水系统排水能力和内涝风险。 虽然取得了较多成果，但大部分研究是在水动力模型基础上模拟运行的，没有建立契合区域特点的数学模型进行模拟预报［13-15］。ARIMA（Auto-Regressive Integrated Moving Average）模型全称为自回归积分滑动平均模型，其基本思路是将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。 ARIMAX 模型能更好地表达系统中多元时间序列的变化规律，建立了除其自身的变化规律外，含有多个输入变量的很多时间序列模型［16］。 左其亭等［17］以塔里木河流域为典型实例，将ARIMAX 运用到了水资源动态承载力预测中，通过构建径流与气温、降水等气象因子的ARIMAX 动态回归预测模型，分析计算RCP8.5、RCP 4.5和RCP2.6 三种气候情景下塔里木河流域未来不同水平年水资源动态承载力。 将ARIMAX 应用到城市内涝预报中，一方面城市内涝除有其自身的变化规律外，还会受到其他多个时间序列的影响，比如降水时间序列，适用于ARIMAX 模型的构建条件；另一方面，通过样本数量积累和动态更新训练，可建立更加精准的ARIMAX 计量模型。 相对其他方法，ARIMAX 模型能够更快实现内涝预报准确率的提高，从而有效增强城市管理和防洪避灾能力。

1 ARIMAX 模型及构建过程

暴雨产生的城市内涝积水，除了积水深度是时间序列外，还受到降水时间序列的影响，因此将降水过程也作为城市内涝积水的研究范围。 应用多元时间序列ARIMAX 模型，建立较为完整的预报内涝积水深度计量模型，更好地描述降水量与积水深度之间的关系，从而有效预测城市内涝积水深度及其变化过程［18］。

1.1 ARIMAX 模型

ARIMAX 模型的构造思路：假设响应序列（因变量序列）yt和输入变量序列（即自变量序列）x1t、x2t、 …、xkt均为平稳序列，先构建响应序列和输入变量序列的回归模型，如式（1）所示。

式中：Ψi（B）为残差序列自回归系数多项式；Yi（B）为残差序列移动平均系数多项式；at为零均值白噪声序列。

动态回归模型的建立是基于响应序列与自变量序列存在长期均衡关系的假设而实现的，并不是所有的序列都可以建立动态回归模型，只有存在长期均衡关系的序列才适合建立动态回归模型。

1.2 模型建立过程

第1 步：对响应序列yt和输入变量序列x1t、x2t、…、xkt进行平稳性检验。

第2 步：对经过适当变换及差分后平稳的输入序列x1t、x2t、…、xkt运用ARIMA 模型，产生白噪声序列，如式（4）所示。

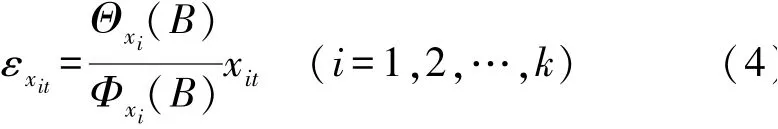
第3 步：对经过适当变换及差分后平稳的响应序列yt运用ARIMA 模型， 产生残差白噪声序列，如式（5）所示。

2 研究区域及数据来源

2.1 研究区域背景

开封市位于黄河下游，河南省中东部，东经113°51′51″—115°15′42″，北纬34°11′43″—35°11′43″，总面积6 444 km2，主城区面积546 km2［21］。 境内河流众多，分属黄河和淮河两大水系。 属暖温带大陆性季风气候区，年均气温为15.2 ℃，年均降水量为627.5 mm，降水集中在夏季7—8 月。 区域内地势平坦，土壤多为黏土、壤土和沙土，发生降雨时不能将雨水有效就地下渗利用，遇到暴雨，市内易形成多个内涝积水点，严重影响城市的防洪安全和居民出行。 因此，开展城市暴雨内涝预报研究显得非常迫切和必要。

2.2 开封“7·20”特大暴雨降水过程

开封市主城区内共有7 个气象站，分布于主城区4 个区内。 其中：龙亭区面积最大，有3 个气象站；顺河区有2 个，鼓楼区和禹王台区各有1 个。 将7 个气象站编号为A～G，其中A 站为国家气象站，B ～G 站为区域加密气象站。 国家气象站数据2021 年综合传输质量为99.88%，区域站为99.22%，各站数据可用率均为100%。

根据开封气象站监测数据，2021 年7 月20 日0时至22 日8 时7 个气象站逐小时降水过程如图1 所示。 最大降水强度出现在7 月20 日22 时，A 站达到103.4 mm／h；最大3 h 累计降水量也出现在A 站，为157.0 mm；最大48 h 累计降水量仍出现在A 站，为354.7 mm，该值已达到开封年平均降水量627.5 mm 的56.5%。 7 个站的平均56 h 累计降水量为345.1 mm。根据7 个气象站覆盖的范围和泰森多边形构造原理，将开封主城区研究区域剖分为7 个多边形，每个多边形中包含1 个气象站和1～4 个内涝监测站，每个内涝积水点到相应气象站的距离最近。 其中G 站距离内涝监测站较远，无最近关联站，因此未参与模型确定。

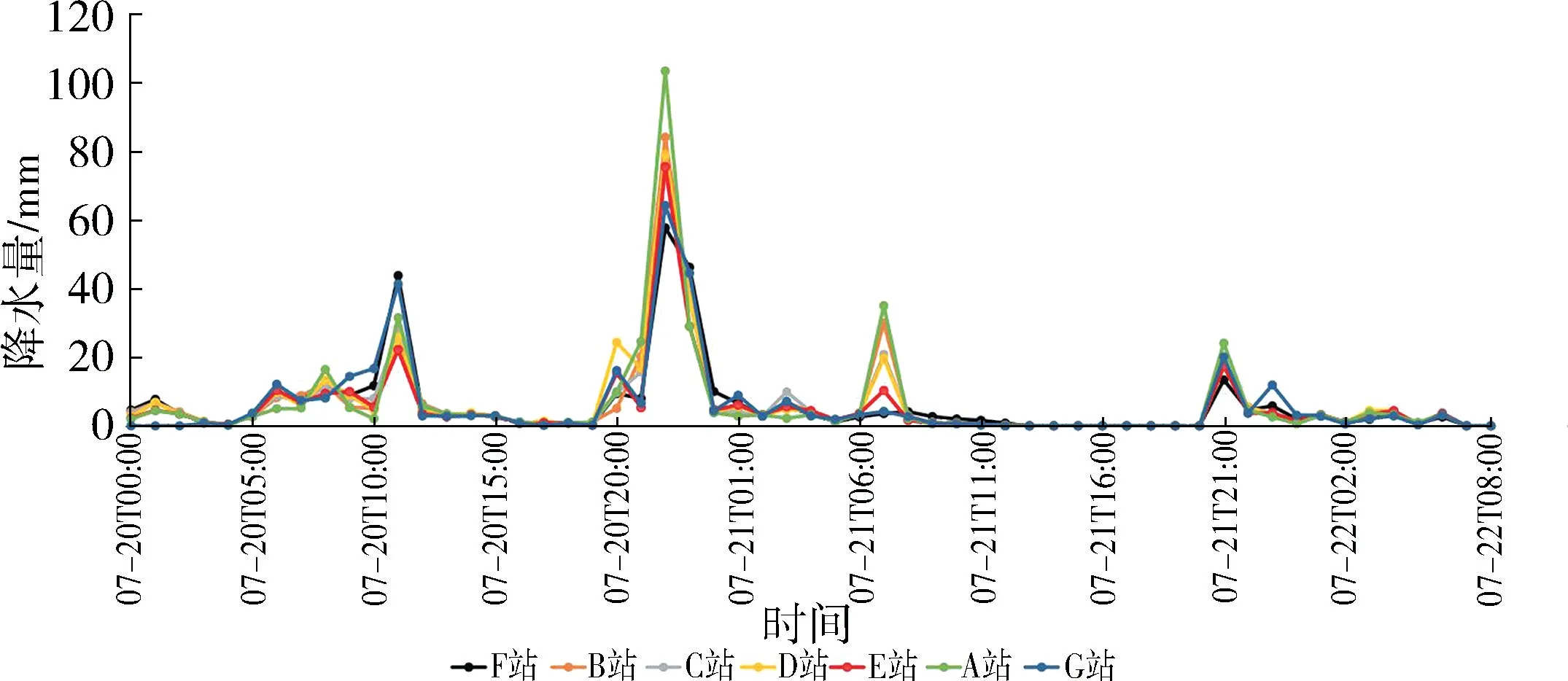
图1 开封市“7·20”特大暴雨降水过程（56 h）

2.3 开封“7·20”内涝数据来源

根据开封市城区内易发生内涝积水的位置，选择了12 个内涝自动监测站作为研究对象，在城市的东、西、南、北4 个方向均选择不少于2 个监测站，并在编号中数字后进行方位标注，与气象站的对应关系见表1。

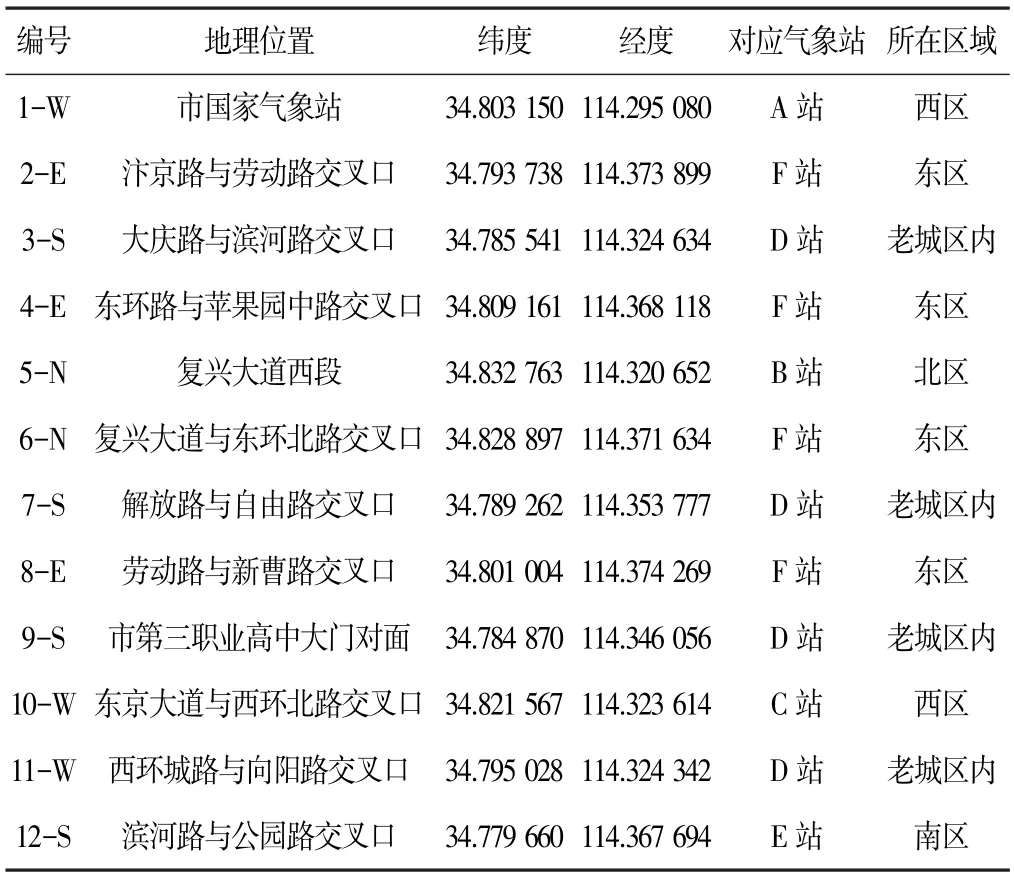
表1 开封市内涝自动监测站位置

3 城市暴雨内涝预报模型确定及精度检验

使用2018—2020 年汛期（5—9 月）开封市主城区气象站逐小时降雨量数据和内涝监测站积水深度数据，对市区出现的积水个例与同期降水强度进行相关统计分析，对数据进行收集和整理。

3.1 数据预处理

为去除数据中的异常值且保证道路积水是由降雨导致的，通过滑动窗口法对积水数据做以下预处理：

（1）若当前时段t没有降雨，t-1 时段没有积水，而当前时段有积水的，将积水数据计为0。

（2）当前时段t没有降雨，积水深度为a，t-1 时段没有降雨，积水深度为b，若b＞a，则令b＝a。

（3）若t-1 时段没有降雨，积水深度＜3 cm，t时段没有降雨，积水深度＜3 cm，则令t时段积水深度为0。

3.2 时间序列平稳性检验

城市内涝积水深度预报是一个多元时间序列分析问题，采用ARIMAX 模型实现积水点位的积水深度预报。 ARIMAX 模型只适用于平稳型数据序列，需要对预处理的数据序列进行时间平稳性检验以及白噪声检验。 在一个自回归过程中，如果滞后项系数为1，就称为单位根。 当单位根存在时，自变量和因变量之间的关系具有欺骗性，因为残差序列的任何误差都不会随着样本量增大而衰减，也就是说模型中的残差影响是永久的。 这种回归又称作伪回归。 如果单位根存在，那么这个过程就是一个随机漫步（Random Walk）［18］。

时间序列模型平稳性检验常用的方法是ADF 检验（Augmented Dickey-Fuller test），也称单位根检验。ADF 检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。 ADF 检验的H0假设就是存在单位根，如果得到的显著性检验统计量小于3 个置信度（10%，5%，1%），则对应90%、95、99%的把握拒绝原假设。 对选择的开封市主城区A、B、…、F 气象站降水时间序列和12 个内涝监测站的积水时间序列进行ADF 检验，结果都满足平稳性要求，见表2。

表2 降水及内涝积水时间序列ADF 检测结果

3.3 白噪声检验

通过对降水和内涝时间序列进行白噪声检验，计算的P值均远小于α（0.05），即拒绝原假设，序列为非白噪声。

3.4 模型确定与定阶

绘制开封12 个内涝点的积水深度与对应降水量的自相关系数和偏自相关系数图（见表3）。 可以看出，所有内涝点二者皆拖尾，对时间序列进行差分操作后，初步选用模型为ARIMAX（p，0，q）。 下一步需确定模型参数p和q的值，通常使用贝叶斯信息准则（BIC）确定模型阶数。 设定p值范围为0、1、2、3，q值范围为0、1、2、3、4、5，对其进行组合，分别计算其BIC。选择BIC 最小的p和q为模型的阶数，为12 个内涝点ARIMAX 模型的最终形式，见表3。 对模型预测的结果进行白噪声检验以确认建模效果，设定滞后阶数为1、6、12 的白噪声检验结果表明，该模型在3 种情况下的P值均远小于0.05，说明预测模型拟合效果较好。确定ARIMAX（p，d，q）中的参数后，利用Python 中Pyflux 软件包，输入时间序列以及p、d、q参数值后即可自动生成模型。

表3 开封市12 个内涝点的ARIMAX 模型参数

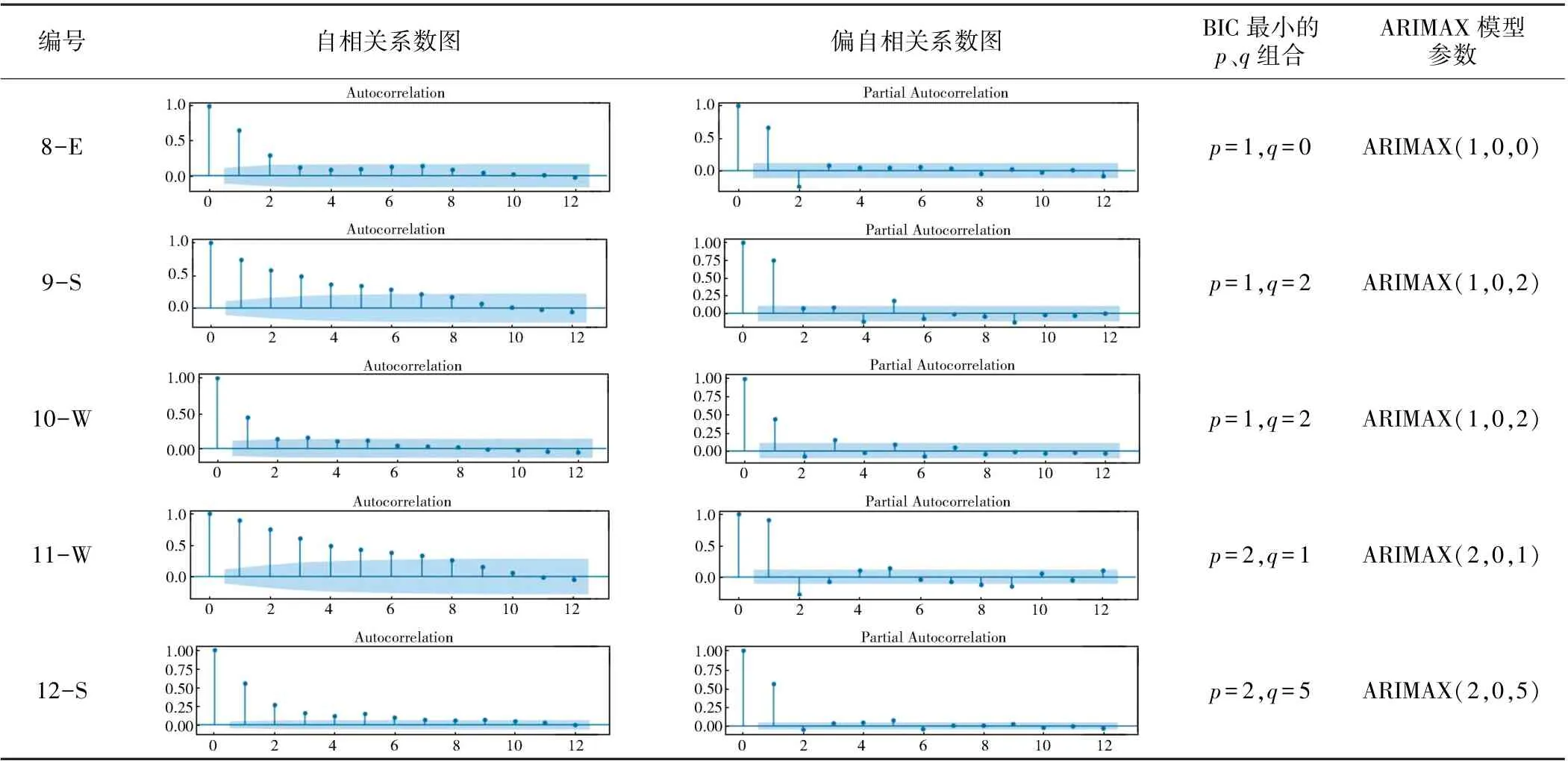
续表3

3.5 模型精度和预测检验

为了检验模型的精度，将基于12 个内涝点建立的ARIMAX 模型进行内涝预测，并计算预测值与实际内涝积水过程的MAE（平均绝对误差）、MSE（均方误差）、RSME（机器学习误差）。MAE又叫平均绝对离差，是所有单个观测值与算术平均值的偏差的绝对值的平均值；MSE是反映估计量与被估计量之间差异程度的一种度量，其可避免误差相互抵消的问题，能准确反映实际预测误差的大小；RMSE为均方根误差，能够衡量观测值与真实值之间的偏差，常作为衡量机器学习模型预测结果的标准［19］。 利用2018—2020 年开封主城区暴雨数据对模型进行训练，12 个内涝点预测的3 种误差值见表4。 其中选择了4 个典型点的降水及内涝实测过程与模型预测过程进行对比，如图2 所示。

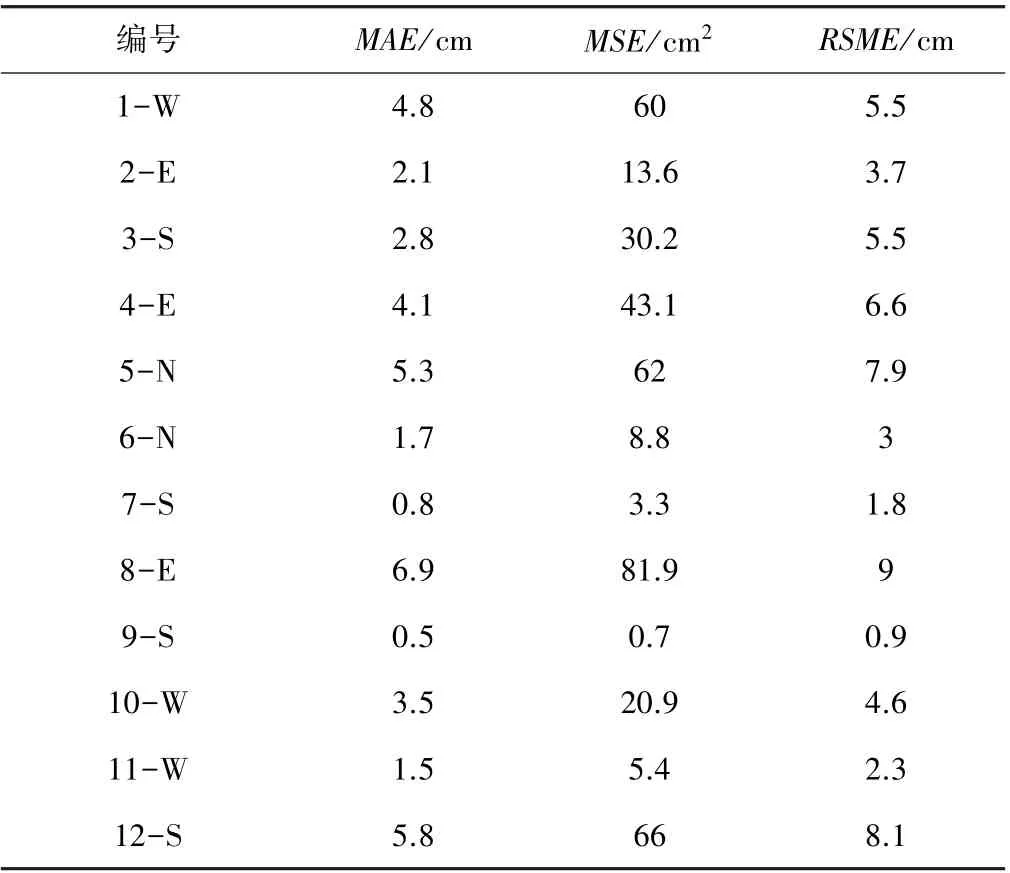
表4 12 个内涝点ARIMXA 模型内涝模拟误差

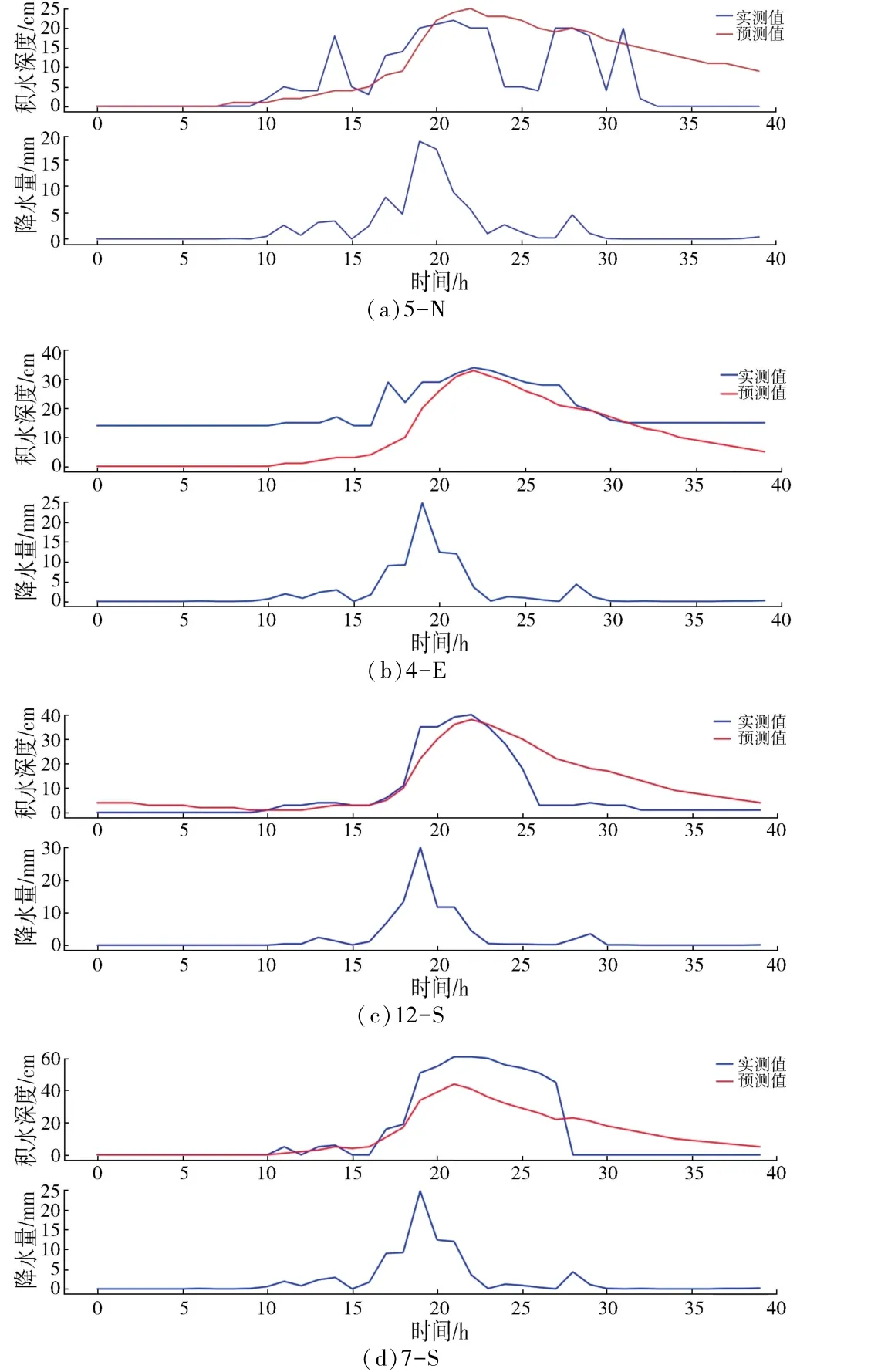
图2 降水及内涝点积水深度实测过程与模型预测结果对比

4 基于“7·20”特大暴雨的内涝预测结果分析

将开封“7·20”特大暴雨的降水过程自7 月20日20：00 开始至7 月21 日20：00 结束共计24 h，作为时间序列输入到12 个内涝监测站的ARIMAX 模型进行预报，并对比12 个内涝监测站的实测数据（见表5）。

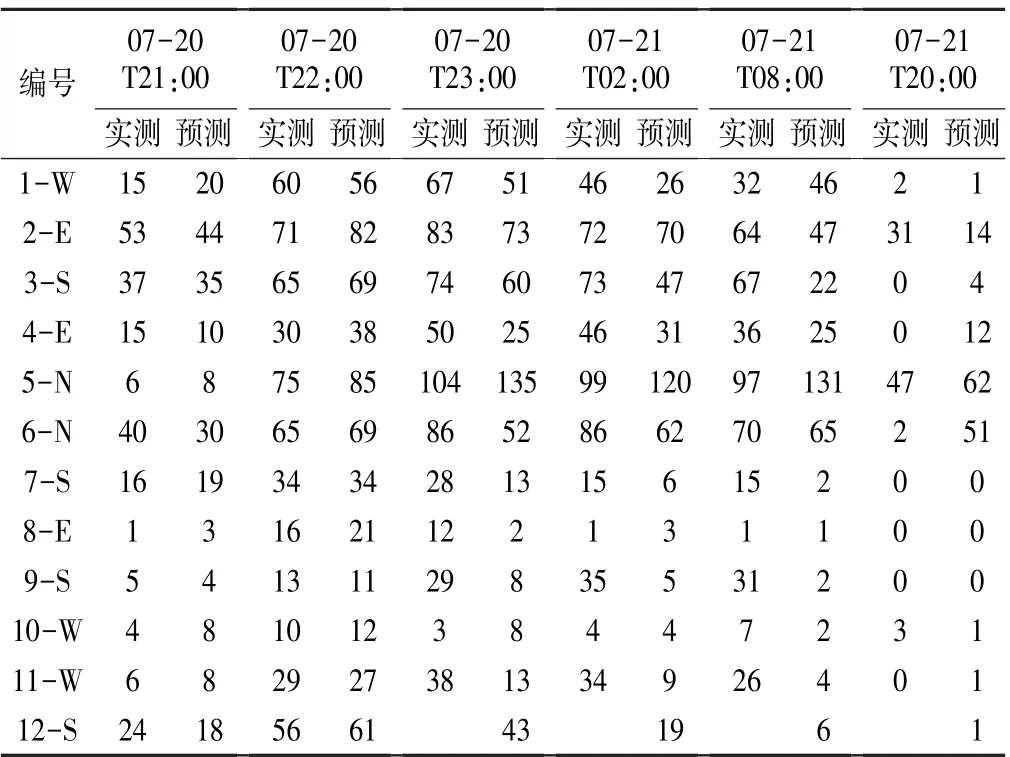
表5 12 个站内涝积水深度实测值与预测值比较 cm

根据表5 的对比结果，1 h 预测误差为1 ～10 cm，平均绝对误差4.3 cm；2 h 预测误差为0 ～11 cm，平均绝对误差4.8 cm；3 h 后平均绝对误差明显增大，超过15 cm。 积水深度在20 cm 以内时误差较小，50 cm 以上误差较大。 降水2 h 内12 个站内涝预报效果较好；随着降雨持续6 h 后，积水深度的预测值出现了一些偏差；到12 h 后，排涝泵站的启动及其他应急预案的处理和干预，预测值与实测值的偏差较大。 总体认为短期内涝预报效果不错，在12 个站中，7-S、9-S 两个站的预报效果较好，这两个站均位于老城区。

对产生误差的原因进行分析，认为“7·20”特大暴雨形成机理极为复杂，预测难度超出目前我国在线运行的气象模型的预测能力。 在本次预测过程中，1～2 h 降水预测以每6 min 观测的雷达加密观测数据为基础，应用光流法外推技术实现短时临近降水预测。 据评估，20 日20 时0 ～2 h 降水量级预测平均准确率为80.5%，误差相对较小。 3～12 h 降水预测使用20 日8时气象数值模式预测结果，暴雨预测准确率不足20%，预报误差还会随时间延长逐渐增大，严重制约了积水深度预报精度。 在积涝中后期，积水深度还受到增设排涝泵站等设备及其他人为干预影响，不能真实反映实际积涝水平。 另一方面，建模初期可用样本数量有限，后续随着可用样本数量积累，动态更新训练模型，会得到更精准的预报结果。

5 结 论

城市内涝积水深度预报是一个比较复杂、影响因素较多的问题，受到下垫面、排水管网、地形等众多因素的影响，而过量降水是导致城市内涝的主要原因。为了精准地对降雨后内涝进行预报，引入了ARIMXA模型，将降水作为时间序列输入，构建开封市12 个内涝监测站的ARIMAX 模型。 利用2018—2020 年汛期（5—9 月）开封市自动气象站逐小时降雨量和12 个内涝监测站逐小时积水深度数据，将出现的积水个例与同期降水强度进行相关统计分析，让模型经过学习训练提高其精度。 以“7·20”特大暴雨过程为例，检验模型预报能力。 经验证，在开封12 个内涝监测站采用ARIMAX 模型预测积水深度的思路是可行的，预报精度2 h 内效果较好，在6 h 内也是可以接受的。 后续研究中一方面将建立基于临界降水的暴雨积涝预警模型，利用视频监控数据、积涝点监控数据对暴雨积涝预警模型进行动态智能订正，提高城市内涝预测预报的准确性；另一方面，通过与站点环境（下垫面、排水管网、地形等）相似类比方法，建立其他区域的积水深度预测模型，为城市内涝预报提供新的思路，并为城市防洪减灾、构建预警系统等提供新方向。