一道高考解析几何题引发的头脑风暴
——探究圆锥曲线中定点、定值之间的微妙关系*
胡蓓蓓 (江苏省无锡市市北高级中学 214000)
今年新高考全国I卷的解析几何大题让人颇感熟悉,笔者在二轮复习备考中,就曾以2020年新高考全国I卷的解几压轴题为引,在课堂上借助思维导图,组织了一场关于“探究圆锥曲线中定点、定值之间微妙关系”的头脑风暴,带领学生大胆猜想、验证,师生共同经历定点、定值问题的“前世今生”,从而深刻理解了这类经典问题的来龙去脉.
1 问题提出
综观近年的高考试卷,圆锥曲线与方程的考点变化不大,考查学生的运算能力,同时需要学生在较短时间内选择合理的路径,快速、准确解题.高三复习时要强化这方面能力的训练,如果学生能够对解析几何的典型结论有所了解,常能快速捕捉到解题关键,找到解题思路,顺利攻破压轴题.

(1)求椭圆C的方程;
(2)点M,N在椭圆C上,且AM⊥AN,AD⊥MN,D为垂足,证明:存在定点Q,使得DQ为定值.
作为高考考场上的压轴题,如何最完美地完成这道题目是我们平时学习过程中需要共同探寻的,而如何完美地给学生呈现这道高质量的高考压轴题,让他们能够更好地理解题意,以一题通百解,则正是我们为人师者应该去思考的.
2 问题分析
引例已知A,B为抛物线y2=4x上异于顶点的两动点,且满足以AB为直径的圆过顶点.求证:直线AB过定点.
师生(分析):当直线AB的斜率不存在时,易得过定点;当直线AB的斜率存在时,设lAB:y=kx+m,要证明直线过定点,解题目标就是设法建立k和m的关系,从而寻找到条件中的唯一等量关系——垂直.(板书详细解题过程,略)
师:接下来请同学们独立完成2007年的山东高考解几题——
椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆C的标准方程;
(2)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
师:如果我们把椭圆方程一般化,定点还存在吗?
学生如醍醐灌顶:原来这个结论是可以一般化的.学生受到启发,进一步思考:如果是双曲线,是不是也有同样的结论呢?教师首先肯定了学生的想法,继而鼓励他们继续猜想.
师:同学们,类比、归纳、猜想都是我们数学学习中非常重要的思维方式,我们要学会利用已有的一些知识进行大胆猜想,这样我们就可以获得更多更新的知识,而这正是数学学习能力的体现.同学们如果在平时就能注意这样去思考、解决问题,我相信大家的数学学习一定会越来越好,解决问题的能力也会越来越强!在猜想过程中,同学们可以横向、纵向地进行比较猜想,也可以正向、逆向进行思考,还可以从特殊到一般地进行归纳猜想,等等.好了,现在就请同学们插上思考的翅膀,一起尽情地猜想吧!
3 问题推广
猜想1 若在圆锥曲线顶点处相互垂直的两条直线与椭圆交于A,B两点,则直线AB必过定点.
猜想2 若圆锥曲线任意点处相互垂直的两条直线与椭圆交于A,B两点,则直线AB必过定点.
猜想3 在圆锥曲线任意点处作两条直线分别交圆锥曲线于A,B两点,若斜率之积为定值,则直线AB必过定点.
猜想4 在圆锥曲线任意点处作两条直线分别交圆锥曲线于A,B两点,若直线AB过定点,则两条直线的斜率之积为定值.
……
板书(即直线过定点⟺斜率之积为定值)
师:恭喜同学们,你们的猜想都是正确的!刚才我们从特殊到一般进行猜想,当然也可以寻找特殊情况来验证自己的猜想是否正确,如猜想3.类比圆的图象性质,椭圆的结论便一目了然(图1).

图1
请同学们课后完成两个作业:(1)运用今天学习到的解析几何通法证明一下自己的猜想或者其他同学的猜想;(2)从我们做过的高考真题或模拟题中,寻找一道与我们猜想的结论一致的解析几何题,并把它解答出来,我们会发现原来我们同学也是可以做命题老师的,而那些神秘的高考题,其实就是我们平时遇到的问题,并不可怕.
最后老师也来猜想一个结论:如果我们把斜率之积改为斜率之和,又会有怎样的结论呢?还是直线过定点吗?
我们同样可以遵循前面的研究方法继续探究.先从特殊的斜率之和为0的情况开始思考,会发现两个交点所在的直线并不过定点,但是这条直线的斜率却是一个定值.证明方法如图2所示.

图2
这正是解析几何问题最典型的两条思考途径,今天的第三个作业就是请同学们课后把这两种证明方法完整地书写出来.而这恰恰正是今年新高考全国I卷解析几何大题的出题背景.
4 问题解决

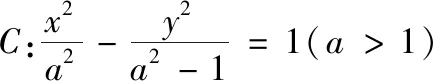
(1)求l的斜率;

5 问题反思
通过上述对定值、定点之间千丝万缕微妙关系的梳理,我们再来看2022年新高考I卷的这道解析几何大题,发现它的身上同样承载着启动一场盛大头脑风暴的重要使命:它是2021年新高考全国I卷的解几压轴题结构的一个退化情形,其本质相同.2021年的这道解析几何题是圆锥曲线中的一个经典性质,也是一个老生常谈的结构,在以前诸多的数学联赛及全国高考卷中屡见不鲜,大家可以查阅研究,如2011年全国II卷、2014年大纲卷等.而2022年考查的退化情形也是高考中的常见问题,如2009年辽宁卷、高中数学联赛卷中还考查了它的逆命题等.
由此可见,在高三最后临近高考的宝贵时间里,教师要精选典型例题,以高考题为载体,带领学生跳出题海,唯有让思维跳跃,才能让学生从千头万绪的复习中抽身出来,获得对问题的真知灼见,从而以不变应万变,从容应对高考试题!
6 教学反思
最后笔者对本堂课的设计作如下简单的教学反思:
·在课堂上开展问题探究活动,增强学生解决圆锥曲线问题的信心与能力,巩固圆锥曲线的相关知识与方法.问题探究活动的过程,不是简单的一题多解,而是不断优化求解思路、促进思维发展、提升核心素养的过程.
·探究活动以小组形式开展,大家既有分工又有合作,还有小组交流和全班交流.每位学生都有参与学习和交流的机会,即便一些基础与学力较弱的学生也能获得积极的情感体验,提高数学学习的兴趣与动力;而数学能力较强的学生更能发挥自己的特长与优势,在带领小组学习、交流的同时,获得成功的体验.对教师而言,预估了学生提出的大部分解法和猜想,但也有很多学生的思维火花超出了教师准备的教学内容,属于生成性教学资源,弥足珍贵.
·作业设计多元化.本节课安排的课后作业中既有反思类作业又有实际操作类作业,既有研究类作业又有分层类作业.通过开发多元化的作业任务,既让学生把课堂内容回顾一遍,又能有所延伸,把很多课上来不及仔细思考的内容变成学生的作业,充分发挥其自主学习力,一箭双雕,让作业与课堂一起熠熠生辉.
·课堂活动评价采用自评、小组成员互评和教师评价的综合评价方式,能够更加客观地对学生的学习行为进行评价,形成较为完善的评价机制.

