小型化高稳定性频选设计与等效电路分析

徐 娟，赵 敏，赵建平

(曲阜师范大学 网络空间安全学院，山东 曲阜 273165)

0 引言

频率选择表面[1-3]作为一种空间滤波器是由金属贴片或缝隙结构形成的一维或二维周期阵列结构，具有带通或带阻的频率选择性。这使得其在雷达隐身天线罩、反射面天线系统中有广泛的应用。随着研究的逐渐深入，性能优良，结构设计巧妙的单频、双频频选不断涌现，设计者大多从频选单元的角度着手，通过改变频选单元的结构，级联形式等实现中心频率的谐振。从单元结构的新颖性出发，Liu Ning[4]设计了一款由四个螺旋三角形在单元格中间对称连接组成的频选单元，该款频选在2.7 GHz具有稳定的谐振频率，尺寸为0.0558λ0×0.0558λ0，与传统的交叉偶极子相比，频选尺寸减小97.7%。为实现频选结构的平面一体化，Wu Bian[5]等人提出了一款基于石墨烯的新型双极化频率选择性吸波器，将四个金属谐振电路与正方形石墨烯薄片连接，形成中心对称的石墨烯-金属杂化结构，利用石墨烯的全向电阻特性在16 GHz频段实现插入损耗0.15 dB的传输窗，避免了焊接多个集总电阻，便于实现结构的平面一体化。此外，通过加载有源器件、结合基片集成波导结构也是频选设计的新思路[6，7]。双频频选的设计主要包括了嵌套思想、分形思想、级联思想等三种思路，一款性能优良的双频频选通常融合了两种或多种设计思想。

从等效电路[8]角度设计频选单元是一种新思路，以准静态场为前提，建立LC谐振回路，再根据金属贴片的电感特性与缝隙的电容特性，设计对应的FSS结构。利用等效电路法设计、分析频选的传输特性具有速度快、求解方便的优势。

本文结合等效电路模型设计了一种单层结构的方形环路缝隙单元和“箭头+Y”形单元，两种结构分别实现毫米波频选的单频和双频带通特性，仿真分析了入射波以不同入射角度以及不同极化方式[9]入射时，FSS 的频率响应特性。结果表明，“箭头+Y”形结构可以有效抑制栅瓣的产生，并且对不同入射角度和不同极化方式的电磁波具有较好的稳定性，本文所提出的FSS可用于毫米波频段FSS天线罩的设计应用。

1 单频频选设计与等效电路分析

1.1 单频频选设计

从等效电路设计单频带通滤波器[10-12]的角度出发，建立如图1所示的谐振电路，即L2、C串联并与电感L1并联的电路形式，Z0为自由空间波阻抗，根据等效电路理论计算等效导纳

(1)

相应的，其等效阻抗可以表示为

(2)

图1 等效电路模型

图2 方环缝隙频选单元

表1 方环缝隙频选单元尺寸

在等效电路与频选结构的对应关系中，电感通常用金属贴片描述，电容则通过金属缝隙表示，且一种等效电路可以对应多种不同形式的频选结构，二者并非是一一对应的关系。根据图1所示的等效电路，设计了一款方形环路缝隙频选单元，如图2所示。另外，图2中给出了单元结构和电感、电容的对应关系，表1为方环缝隙频选单元尺寸。

相反，亦可以从频选单元的尺寸参数推导等效电路的元件值，同样对于图2所示的方形环路缝隙结构，d,p,s,g为方环缝隙的几何尺寸，其中d为缝隙的外侧边长，p为单元周期，s为缝隙的宽度，g为外侧方环金属线宽，(3)～(7)给出利用模型变量计算元件值的公式

wL1=cosθF(p,g,λ,θ) ，

(3)

(4)

(5)

(6)

(7)

式中εeff=0.5(εr+1)，函数F(p,g,λ,θ)，F(p,d-2s,λ,θ)，F(p,d,λ,θ)，F(d-s,s,λ,θ)均可通过文献[13]计算得到，w为角频率，可表示为w=2πf，λ为频选单元的工作波长，θ为相对于法线方向的入射角。公式(5)和公式(6)中的BC1，BC2和Y0为应用于公式(7)的中间变量，无物理含义。

1.2 单频频选全波仿真与等效电路对比

在电子设计自动化软件ADS中仿真，分别求解反射系数与传输系数，其中C=0.036 pF，L1=49.54 pH,L2=20.12 pH。另外，运用电磁仿真软件HFSS对方环缝隙频选单元进行全波仿真，设置主从边界条件和Floquet激励求解，并将计算结果与通过等效电路得到的结果进行对比，如图3(a)、(b)所示。反射系数与传输系数均在谐振频率100 GHz处吻合良好，进一步说明等效电路方法对分析和设计频选单元具有较好的指导作用，且分析思路清晰，计算简便，大大提高了频选的分析和设计效率。由于等效电路模型未考虑介质基板的损耗、基板厚度，忽略了金属贴片和缝隙之间的耦合现象等，谐振环境较为理想，使得其在分析精度上略有不足。

图3 等效电路与全波仿真性能对比

2 “箭头+Y”形双频频选设计

2.1 双频等效电路设计

基于图4(a)所示的等效电路设计了一款“箭头+Y”形频选，结构设计中采用嵌套和分形[14]的思想，将介质基板等效为传播常数为β1和特征阻抗为Z1的短传输线，其中Z0为自由空间波阻抗，β0为自由空间的传播常数。从电路原理的角度推导电路整体导纳，可由式(1)表示为

(8)

(9)

令lm[YFSS]=0，得到关于w的一元四次方程

L1C1L2C2w4-(L1C1+L2C2+L2C1)w2+1=0。

(10)

对上述一元四次方程进行求解，得到两组互为相反数的根

(11)

(12)

其中

(13)

(14)

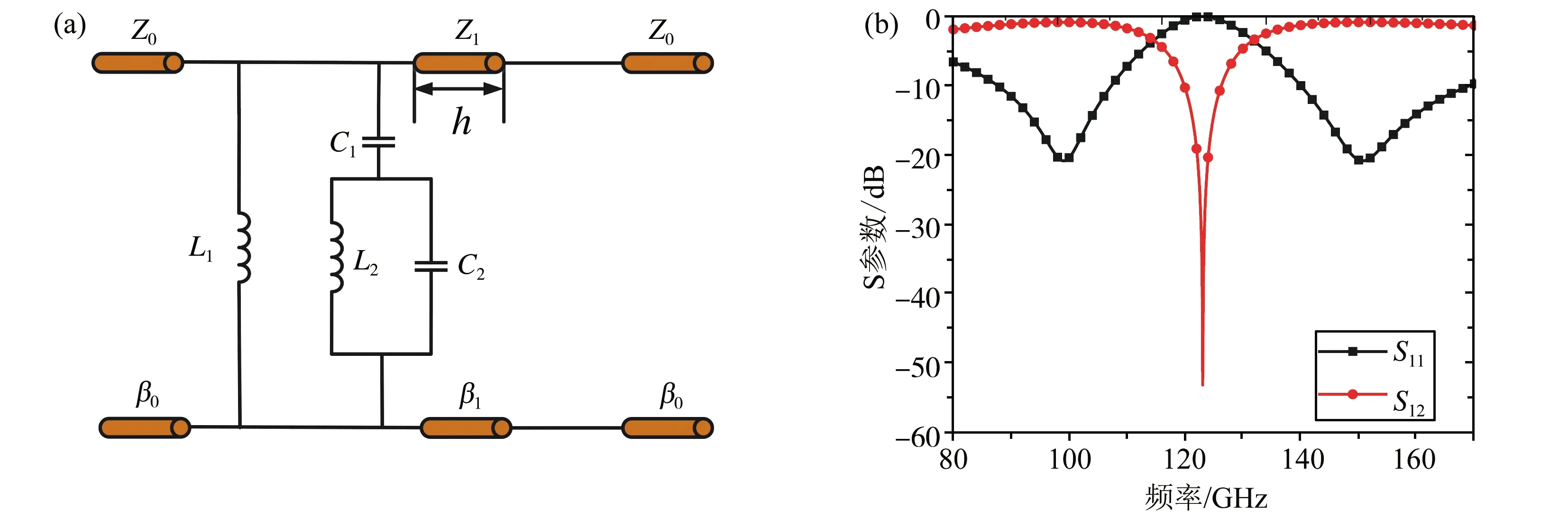
注：(a) 等效电路；(b) S参数。图4 “箭头+Y”形频选等效电路及S参数

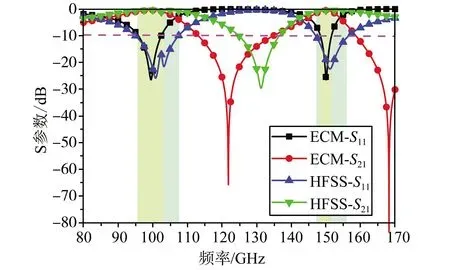
图5 “箭头+Y”形频选等效电路与全波仿真对比

由式(11)和式(12)可知，通过合理设置L1、L2、C1、C2的取值能够使该方程产生两个大于零的解，说明图4(a)的等效电路有两个有效极点，能够实现双频谐振，电路中元件值为L1=5.556 pH，L2=45 pH，C1=0.256 pF，C2=0.045 pF。图4(b)给出基于等效电路的S11(反射系数)和S21(传输系数)曲线，证实其工作频点为100 GHz和150 GHz。在电磁仿真软件ADS中进行仿真[15，16]，得到其S参数曲线，并与HFSS全波仿真结果作对比，如图5所示，发现二者可以在100 GHz和150 GHz频点处较好的吻合，进一步证实了分析的有效性。

2.2 “箭头+Y”形频选性能分析

基于对分形和嵌套设计的思路，设计了一款基于嵌套思想并融合了分形元素的“箭头+Y”形双频频率选择表面[17]。该结构由两个改良的环形回路构成，其中内部圆环形回路是以圆环为基础，从垂直于矩形轮廓边长的方向向内延伸了四个Y形枝节，用于增加结构的电长度，便于实现小型化。外部环形回路是以方环为基础，在方环的四个直角处向内延伸了箭头形缝隙结构，该款双频频选能够实现100 GHz和150 GHz处的稳定谐振。图6给出模型的尺寸标注和等效电路模型，经过仿真优化得到模型参数的最终取值，如表2。

运用电磁仿真软件HFSS对“箭头+Y”形FSS单元建模仿真，在空气盒子上下表面添加激励，设置为Floquet端口，空气盒子侧面设置为主从边界条件，介质基板选用介电常数为4.4的FR4材料，其介电损耗正切值tanδ=0.02，介质基板厚度为h=0.0449 mm。

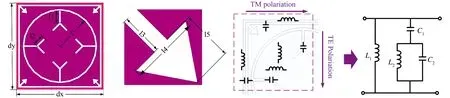
(a) 模型整体标注 (b) 等效电路模型图6 “箭头+Y”形FSS模型尺寸标注

通过图7的S11曲线和S21曲线，发现在TE、TM模式时，该款单元均在100 GHz和150 GHz处产生谐振。其中图7(a)的工作频段为94.6 GHz～107.3 GHz，146.8 GHz～155.6 GHz，100 GHz处回波损耗为-27.74 dB，150 GHz处回波损耗为-22.15 dB。图7(b)的工作频段为92.9 GHz～107.7 GHz，146 GHz～155.45 GHz，100 GHz处回波损耗为-28.53 dB，150 GHz处回波损耗为-22.42 dB。

注：(a) TE模式； (b) TM模式。图7 TE/TM模式传输性能

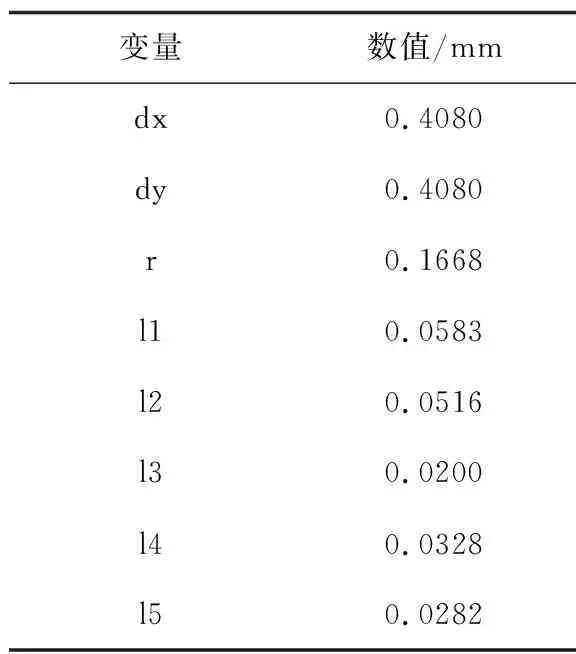
表2 “箭头+Y”形FSS模型变量

为研究“箭头+Y”形频选单元的角度稳定性和极化稳定性，分别分析了TE和TM模式下，不同入射角度下的反射系数和传输系数曲线。通过观察TE模式时的反射系数和传输系数，如图8所示，“箭头+Y”形频选单元在0°、15°、30°、45°的入射角度下，均能在100 GHz和150 GHz有稳定的谐振效应，说明该款频选单元在TE模式下有良好的角度稳定性。低频带3 dB带宽由32.27 GHz减少至25.9 GHz，高频带3 dB带宽由28.21 GHz减少至19.854 GHz。说明TE模式下，随着入射角度的增加，3 dB带宽逐渐减小。

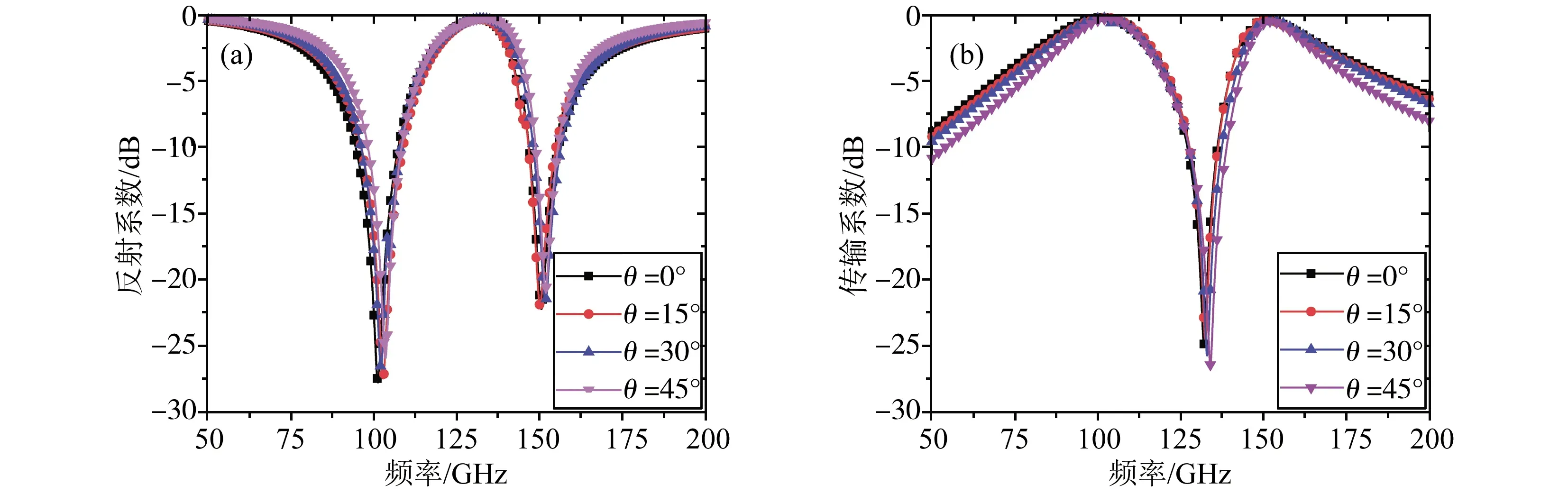
注：(a) 反射系数； (b) 传输系数。图8 “箭头+Y”形FSS单元TE模式角度稳定性

如图9所示，TM模式时随入射角度由0°变化至45°，谐振频点基本稳定在100 GHz和150 GHz，说明该款频选单元在TM模式下有良好的角度稳定性。低频带3 dB带宽由31.71 GHz增加至42.5 GHz，高频带3 dB由25.89 GHz增加至38.15 GHz，与TE模式下的3 dB带宽变化趋势相反。究其原因，对于缝隙形频选单元，TE模式时频选的3 dB带宽会随着入射角度的增大以cosθ的倍数减小；相应的，当入射电磁波为TM模式时，频选的3 dB带宽会随着入射角度的增大以1/cosθ的倍数增大。

为进一步说明双频频选的谐振原理，分析了单元表面的电流分布情况，如图10所示。图10(a)为频选单元工作在100 GHz时的电流分布，外侧箭头形回路发生明显谐振；图10(b)为频选单元工作在150 GHz时的电流分布，内侧Y形回路产生明显谐振，说明低频频点由外部箭头形回路谐振得到，高频频点由内部Y形回路谐振产生，进一步证实了嵌套式双频频选的谐振原理。

注：(a) 反射系数；(b) 传输系数。图9 “箭头+Y”形FSS单元TM模式角度稳定性

注：(a) 100 GHz; (b) 150 GHz。图10 “箭头+Y”形FSS单元电场分布

3 结论

本文基于等效电路设计了方形环单频频选和双频“箭头+Y”形频选单元，通过全波仿真分析了其滤波性能，两款单元均在通带内有良好的角度稳定性和极化稳定性，说明综合运用等效电路法和全波仿真设计频选单元的有效性。通过合理计算其两款单元的尺寸参数，可应用于除毫米波之外的其他频段，有较广的应用范围。