多元线性回归的地应力场反演分析及应用

王志云，于 申，李守巨，杨朔明，樊可为

（1.大连海洋大学海洋与土木工程学院，辽宁 大连 116023；2.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

岩体内的初始应力场直接影响隧道和硐室围岩的稳定性；因此，合理确定地下岩体的应力场对隧道围岩稳定性评估和支护衬砌结构参数选取至关重要。在漫长的地质年代地壳构造运动作用下，岩层会产生褶皱、弯曲、断裂和错动，使得岩层种除了自重产生的应力场之外，还会有2个水平方向的构造应力和1个垂直方向的构造应力。构造应力的大小和方向也可能会随着埋深的增加而发生变化；作为一种最简单的假设，认为构造应力的大小不随深度的增加而变化，是一个常数。该假设可能使地应力的拟合精度下降，但也使得地应力场反演算法的复杂程度大大降低，得到的地应力场分布结果也基本上满足工程建设精度要求。郭喜峰等[1]以清远抽水性能电站为例，研究了地应力场的多元回归分析反演方法，建立了基于最小二乘法原理的地应力场参数计算的法方程的系数矩阵；周春华等[2]以鄂西某隧道工程为例，对地应力场反演方法及围岩稳定性进行了分析；谢洪强等[3]对锦屏水电站坝区初始地应力场进行了回归反演分析；李永松等[4]研究了深圳抽水性能电站的应力场反演方法，提出了4种荷载工况下的加载方法；何少云等[5]基于地应力实测结果，采用多元线性回归方法和三维有限差分法，研究了某水电站地下厂房区域的初始地应力场反演问题；徐中卫等[6]采用多元回归方法、神经网络和遗传算法3种方法，研究了蟠龙抽水蓄能电站地下工程区域的初始地应力场反演问题；李守巨等[7～8]采用优化算法研究了地下厂房岩体应力场的反演问题。

本文提出一种基于求解超定线性方程组的地应力场反演方法，建立地应力场多元线性回归的数学模型，根据现场观测地应力场数据，反演确定线性回归方程的系数，采用有限元模型模拟得到某地下厂房区域的整体应力场分布。

1 地应力场多元回归反演分析方法

为确定地下岩体内的初始应力场和进行开挖后的围岩稳定性，采用水压致裂法或应力解除法进行地应力现场测试，一般需要几个钻孔，以便对测试结果相互验证。某地下厂房处于微风化花岗岩岩体内，在DH008钻孔内布置5个观测点，每个观测点观测3个主应力数值，共15个观测数据。假设岩体内任意观测点的3个主应力分别与岩体的自重（工况1）、大主应力方向（有限元模型x坐标）的构造应力（工况2）、小主应力方向（有限元模型y坐标）的构造应力（工况3）和垂直方向（有限元模型z坐标）的构造应力（工况4）有关。根据现场观测，大主应力方向为N30E；因此，有限元计算模型取x坐标方向为N30E，y坐标方向为N60W，z坐标方向为垂直向上。这样，在有限元计算模型边界上，x、y、z方向均为主应力方向，与坐标轴平行的有限元模型边界上没有剪应力。见图1。

图1 4种典型荷载工况简化加载模型

1.1 地应力场多元线性回归的数学模型

基于多元回归分析的基本原理，以第一个观测点的垂直主应力为例，将垂直主应力的回归计算值SRv作为函数，把有限元在4种荷载工况下分别计算求得的该观测点垂直主应力计算值Sv1、Sv2、Sv3、Sv4作为自变量，则该观测点地应力的垂直主应力线性回归方程

式中：Lz为岩石自重的多元回归系数；Lx为水平大主应力方向构造应力的回归系数；Ly为水平小主应力方向构造应力的回归系数；Lt为垂直构造应力的回归系数。

同理，也可以得出该观测点的水平大主应力和小主应力的回归方程

式中：下标l、s分别表示水平大主应力、水平小主应力，其他符号含义同式（1）。

岩体地应力场反演的目的在于使经过回归分析得到的所有观测点3个主应力与现场观测值的残差平方和最小，定义目标函数J

式中：i表示第i个观测点，i=1，2，3，4，5；Sm为主应力现场观测值。

为求解该极小值，未知数为回归方程的回归系数，令目标函数J对于回归系数的导数等于0，根据复合函数求导规则，推导出

一个观测孔有5个观测点，每个观测点3个主应力观测值，一共15个方程，4个未知数，方程的个数大于未知数的个数，属于超定方程组。MATLAB软件为解决超定方程组问题提供了数值计算精度的保证。根据地勘报告和地应力现场观测结果，确定岩体基本力学参数：密度2 600 kg/m3、弹性模量9.2 GPa、泊松比0.27、抗压强度65.3 MPa。初步假定3个方向上的构造应力作为有限元数值模拟所需假定的边界条件：垂直方向构造应力5.00 MPa、水平大主应力方向构造应力6.0 MPa、水平小主应力方向构造应力3.0 MPa。

1.2 工况1有限元模拟计算

采用岩体实测密度、弹性模量和泊松比，计算在自重作用下所产生的自重应力场。其中，有限元模型底部施加垂直位移为零约束，dz=0；在与x轴垂直的两个平面施加x方向位移为零约束，dx=0；在y轴垂直的两个平面施加y方向位移为零约束，dy=0。在自重应力作用下，岩体内的垂直地应力随埋深的变化

式中：ρ为岩石的密度；g为重力加速度；h为埋深。

水平地应力随埋深的变化

式中：μ为岩石的泊松比。

σv、σhmax和σhmin都是主应力并且水平方向的两个主应力大小相等。有限元计算不同观测点3个方向的主应力见表1。

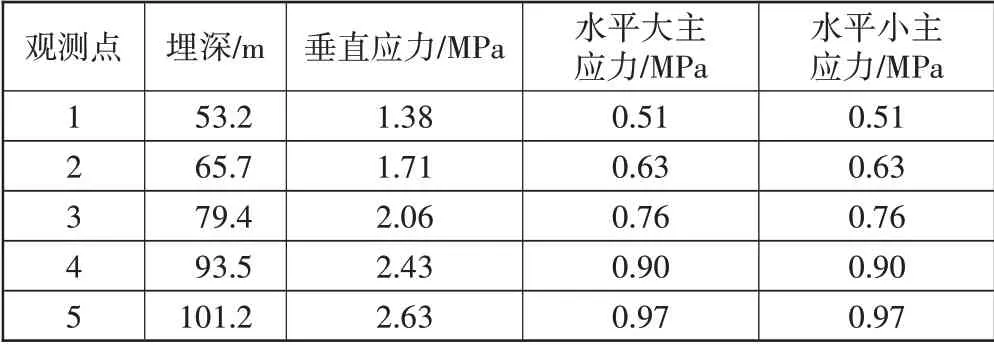
表1 有限元计算工况1不同观测点3个方向的主应力

1.3 工况2有限元模拟计算

取岩体的密度为0，在与x方向垂直的两个边界面施加均匀分布6 MPa的构造应力；而与y方向垂直的两个边界面施加位移为零约束，dy=0；在有限元模型的底部施加垂直位移为零约束，dz=0。不同观测点3个方向的主应力见表2。

表2 有限元计算工况2不同观测点3个方向的主应力

1.4 工况3有限元模拟计算

取岩体密度为0，在与y方向垂直的两个边界面施加均匀分布3 MPa的构造应力；而与x方向垂直的两个边界面施加位移为零约束，dx=0，在有限元模型的底部施加垂直位移为零约束，dz=0。不同观测点3个方向的主应力见表3。

表3 有限元计算工况3不同观测点3个方向的主应力

1.5 工况4有限元模拟

取岩体密度为0，在模型顶部施加5 MPa的局部压力；在与y方向垂直的两个边界面施加位移为零约束，dy=0；而与x方向垂直的两个边界面施加位移为零约束，dx=0；在有限元模型的底部施加垂直位移为零约束，dz=0。不同观测点3个方向的主应力见表4。

表4 有限元计算在工况4不同观测点3个方向的主应力

1.6 超定方程组求解

根据地应力场多元线性回归的数学模型和4种工况下有限元数值模拟结果，确定地应力场多元线性回归超定方程组系数矩阵。

式中：A为超定线性方程组的系数矩阵（15×4）；L为回归方程的系数矢量（4×1）；Sm为现场观测数据矢量（15×1）。

超定方程组的系数矩阵是根据式（5）～（7）及表1-表4，得到MATLAB格式的系数矩阵，排列顺序依次为观测点1垂直主应力在4个工况有限元计算值、大主应力在4个工况有限元计算值、小主应力在4个工况有限元计算值；观测点2、观测点3、观测点4、观测点5的3个主应力4个工况有限元计算值。

另外一种计算回归方程系数的方法是将式（10）两端同时左乘系数矩阵A的转置矩阵AT。

经过变换后，式（11）的系数矩阵为4×4方阵，直接求解该线性方程组就可以得到回归方程的系数。

2 工程应用

在钻孔编号DH008不同高程布置5个地应力测试点，每个观测点观测到的3个主应力，该组观测数据是地应力场反演的依据。见表5。

表5 DH008地应力场现场观测数据

地应力场多元线性回归超定方程组的右端项（列向量）是根据表5按照顺序与系数矩阵排序相对应：观测点1的垂直主应力、大主应力和小主应力；观测点2、观测点3、观测点4、观测点5的垂直主应力、大主应力和小主应力，即Sm列向量。于是，超定方程组的解的MATLAB表达式为

采用MATLAB软件，求解地应力场线性回归分析超定方程组，得到4个线性回归系数。

由于地应力现场观测误差的存在，直接求解超定方程组得到的解有时偏离工程实际。考虑到在地应力现场测试中，垂直主应力的精度最高，采取如下策略求解：根据垂直主应力的观测数据，先确定与垂直地应力相关的两个回归系数（Lz和Lt）；再根据水平大主应力和小主应力的观测数据，确定另外两个回归系数（Lx和Ly）。从表2和表3可以看出，工况2和工况3对垂直主应力没有任何影响；因此，将式（5）简化为

根据5个观测点的垂直主应力数据，可以列出5个线性方程，求解该超定方程组，求出两个回归系数Lz=0.982 7和Lt=0.918 7后，式（6）和式（7）改写为

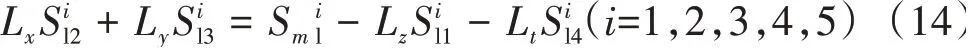
同样根据5个观测点的水平大主应力和小主应力数据，求解10个超定方程组，得到另外两个回归系数Lx=0.859 4和Ly=0.604 4。

为验证所得应力场参数的精度，根据表5中垂直地应力现场观测数据，线性拟合得到垂直地应力随埋深的变化

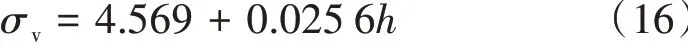
对比式（16）和表5中反演所得到的垂直构造应力可以发现，反演分析和拟合分析所得到的垂直方向的构造应力分别为4.59、4.57 MPa，说明反演方法所得到的地应力场参数是十分准确的。回归反演确定的构造应力：垂直方向应力为4.593 5 MPa、水平大主应力为5.156 4 MPa、水平小主应力为1.813 2 MPa，将回归分析反演得到的回归系数和有限元计算得到的表1-表4带入到式（1）～式（3），得到5个观测点地应力反演预测值。见表6。

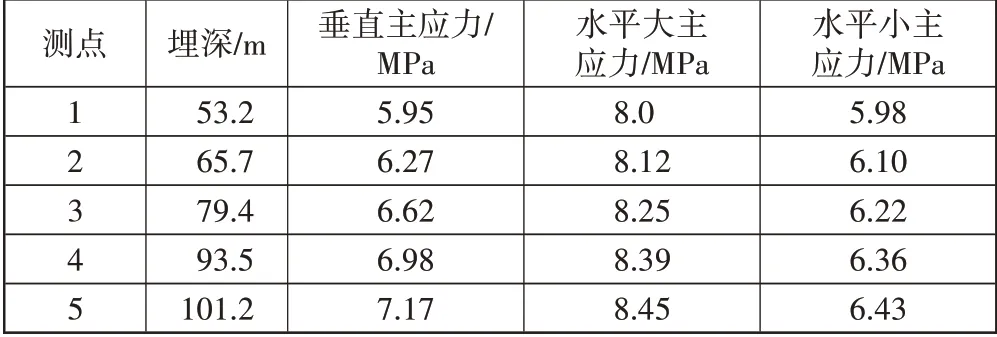
表6 地应力反演预测值

3 结论

1）采用多元线性回归分析方法，建立了地应力场回归分析的数学模型，基于有限元数值模拟方法和现场观测的地应力数据反演确定了地应力场参数。该方法为准确估计该区域的地应力场三维分布特性提供了依据，为后期地下厂房的围岩稳定性评估奠定了基础。

2）计算结果表明，反演分析和拟合分析所得到的垂直方向的构造应力分别为4.59、4.57 MPa，说明反演方法所得到的地应力场参数是十分准确的。相对比而言，垂直地应力场构造应力拟合精度最高，最大相对误差＜2%；水平小主应力方向的构造应力最大误差＜7%，水平大主应力方向的构造应力拟合精度有一定的误差。

3）本文仅给出了基于单个钻孔5个观测点地应力观测数据反演得到的地应力场数据；多个观测孔现场观测数据时，反演方法与单孔的反演地应力场方法类似，只不过随着数据增多，超定方程组的行数更多，线性回归方程的系数个数不变，观测数据有时可能会出现冗余，甚至有些观测数据相互不协调或者相互矛盾的情况。

4）由于岩体地质构造运动的复杂性和不确定性，在某个方向上的构造应力可能不是常数，即有限元计算模型边界上的侧压力（构造应力）分布可能不是矩形，而是一个梯形分布，这时就会增加线性回归方程系数的个数，但会使得反演预测精度进一步提高。