分数阶Klein-Gordon-Schrödinger方程的保能量方法
张利娟,孙建强
(海南大学理学院,海南 海口 570228)
0 引言
分数阶微分方程在科学和工程领域中具有重要的应用[1-2],许多学者对分数阶微分方程的理论和计算进行了大量的研究[3-6].本文利用平均向量场方法和傅里叶拟谱方法计算具有拉普拉斯算子(1<α<2)的分数阶Klein-Gordon-Schrödinger(KGS)方程[7]
(1)
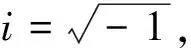
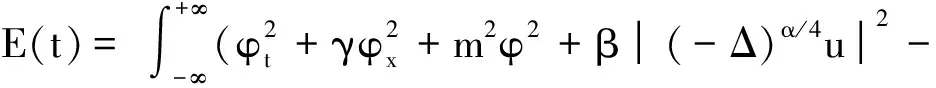
(2)
当α=2,β=1,γ=1时,方程(1)变为耦合KGS方程.在量子场论中,耦合KGS方程是守恒复中子场和实介子场相互作用的数学模型.在耦合KGS方程中,已经发现了许多重要的结论,如M. Ohta[8]分析了耦合KGS方程的稳定性,孔令华等[9]提出了辛方法数值求解耦合KGS方程.分数阶KGS方程是经典耦合KGS方程的推广,分数阶KGS方程(1)的理论和计算越来越受到关注,如黄春妍等[10]证明了分数阶KGS方程的柯西问题的局部和整体的适定性、低正则性,王俊杰等[11]利用守恒的傅里叶谱方法来求解分数阶KGS方程.
微分方程保能量守恒性的数值方法近年来成为保结构算法研究领域的热点,平均向量场方法能较好地保持哈密尔顿系统固有的能量守恒特性.平均向量场方法是1999年由R.I. McLachlan等[12]提出的用于求解哈密顿系统的数值方法,能精确地保持系统的能量[13-14].文献[15-16]已利用平均向量场方法分别求解了薛定谔方程和sine-Gordon方程等,取得了满意的效果.利用保能量算法数值求解分数阶微分方程,目前国内外研究工作还较少.本文将利用2阶平均向量场方法和傅里叶拟谱方法构造分数阶KGS方程(1)的保能量格式.
首先,将分数阶KGS方程转化成辛结构的哈密尔顿系统;然后,介绍了α阶Riesz空间分数阶导数定义,给出了Riesz空间分数阶导数与分数阶拉普拉斯算子之间的关系,利用傅里叶拟谱方法对Riesz空间分数阶导数在空间方向上进行离散近似,得到相应的离散矩阵;再利用傅里叶拟谱方法对Riesz空间分数阶KGS方程(1)进行空间离散近似,得到有限维的哈密尔顿系统,在时间方向上利用2阶平均向量场方法离散哈密尔顿系统,构造出分数阶耦合KGS的保能量格式;最后,利用新格式数值模拟分数阶KGS方程孤立波的演化行为,并对新格式的保能量守恒特性进行分析,得出结论.
1 分数阶KGS方程辛结构的哈密尔顿系统
令u=p+iq,φt=2v,则分数阶耦合KGS方程(1)等价于
(3)
方程(3)可以表示成如下的无限维哈密尔顿系统
dz/dt=JδH(z)/(δz),
(4)
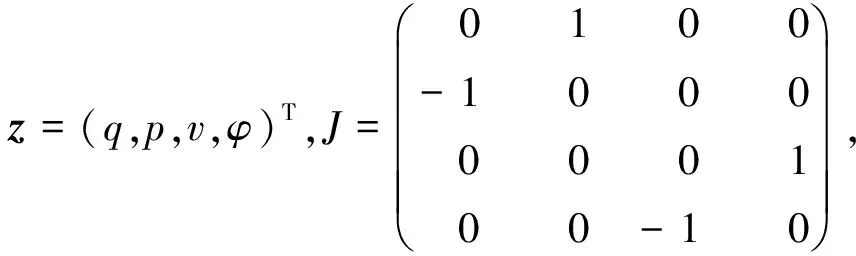
(5)
2 分数阶KGS方程的保能量方法
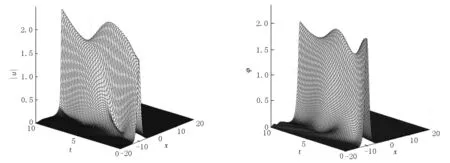
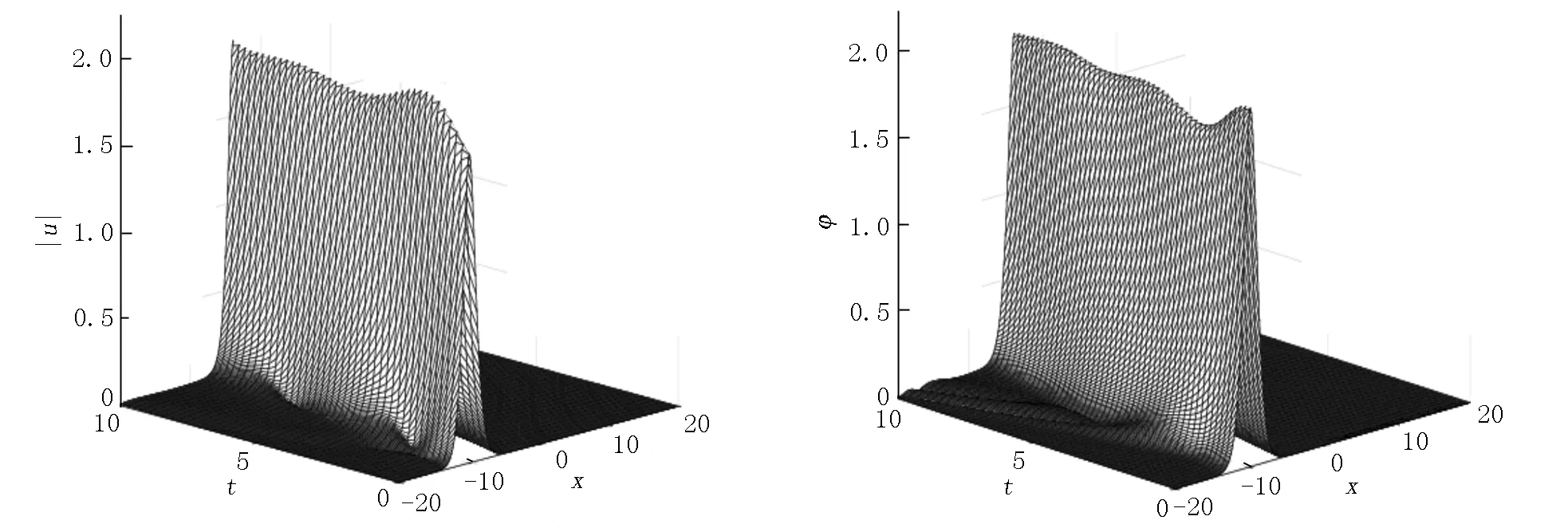
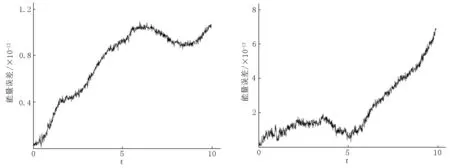
引理1[17]在无限区间(-∞ ∂αu(x,t)/∂|x|α=-1/(2cos(πα/2)Γ(n-α))· (6) 其中n-1<α 在无限区间(-∞ -(-Δ)α/2u(x,t)=-F-1|x|αFu(x,t), (7) 其中F和F-1分别表示傅里叶变换和傅里叶逆变换,有 (8) 在具有周期边界条件或零边界条件的有界区间Ω=(a,b)上,由傅里叶级数定义有 (9) 假设空间积分区间Ω=[a,b],并将Ω进行N等分,N是一个正偶数,空间步长h=(b-a)/N.令xj=a+jh(j=0,1,…,N-1)为空间傅里叶配置点[19].令函数u(x,t)的逼近函数uN(x,t)表示插值逼近(INu)(x,t),有 (10) 由式(9)和式(10)可得 (11) (12) (13) 同时在方程(3)中变量φ关于x的2阶偏导数的谱微分矩阵的元素[17]为 (14) 在空间方向上,利用傅里叶拟谱方法对分数阶KGS方程(3)进行离散.可得到方程(3)的半离散系统 (15) 其中j=0,1,…,N-1,半离散系统(15)可表示为如下有限维哈密尔顿系统 (16) 其中Z=(q0,q1,…,qN-1,p0,p1,…,pN-1,v0,v1,…,vN-1,φ0,φ1,…,φN-1)T, 0和I分别为零矩阵和单位矩阵,相应的哈密尔顿函数为 在时间方向上利用2阶平均向量场方法[15] (17) 和离散哈密尔顿系统(16),可得到如下离散格式 (18) 定理1离散格式(18)能精确地保持哈密尔顿系统能量守恒[15] H(Zn+1)=H(Zn). 证方程(17)可以改写为 (19) 由微积分基本定理可得 (H(Zn+1)-H(Zn))/τ=0. 即定理1得证. 利用新格式(19)对分数阶KGS方程(1)进行数值模拟.定义相对能量误差函数为 RE(t)=|(H(Zn)-H(Z0))/H(Z0)|, 设分数阶KGS方程(1)中变量β=1,γ=1,m=1,α1=1,则初始条件[7]为 图1(a)表示复函数u(x,t)孤立波的模在α=1.2,t∈[0,10]时的数值解,图1(b)表示实函数φ(x,t)孤立波在α=1.2,t∈[0,10]时的数值解,由图1可以看出孤立波数值解的波形光滑且较平稳地随时间传播,与文献[7]的数值结果一致.图2(a)表示复函数u(x,t)孤立波的模在α=1.5,t∈[0,10]时的数值解,图2(b)表示实函数φ(x,t)孤立波在α=1.5,t∈[0,10]时的数值解,由图2可以看出孤立波数值解的波形光滑且较平稳地随时间传播,与文献[7]的数值结果也同样一致.图3表示在分数阶KGS方程中孤立波在α取不同值时数值解的相对能量误差随时间的变化,误差可达10-13,可忽略不计.这表明新格式能较好地模拟在分数阶KGS方程中孤立波的演化行为,并精确地保持方程离散能量守恒性. (a)复函数|u(x,t)| (b)实函数φ(x,t) (a)复函数|u(x,t)| (b)实函数φ(x,t) (a)α=1.2 (b)α=1.5 本文把分数阶KGS方程转化成具有辛结构的哈密尔顿系统,然后利用傅里叶谱方法和平均向量场方法数值离散分数阶KGS方程,得到分数阶KGS方程新的保能量格式.数值结果表明:新格式能较好地模拟分数阶KGS方程孤立波的行为,并保方程的能量守恒性, 验证了格式的保能量守恒性.这说明本文提出的分数阶KGS方程的保能量方法是有效的,为进一步研究其他分数阶微分方程提供了可供选择的数值算法.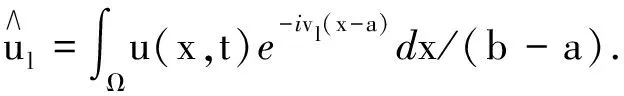

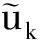
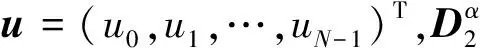

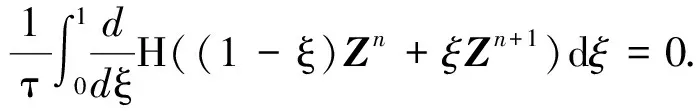
3 数值模拟
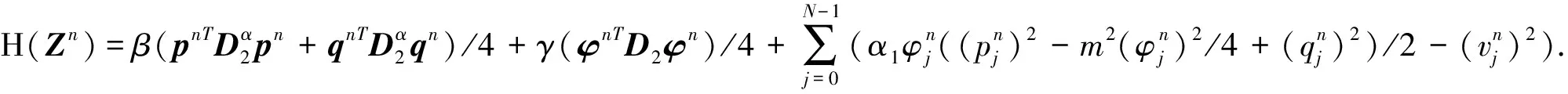
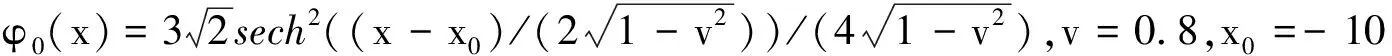
4 小结

